МЕХАНИКА ДЛЯ КВАНТОВОЙ МЕХАНИКИ
Часть 6. Эффект Доплера
.первая редакция 13.04.2014
С. Ю. Юдин http://modsys.narod.ru . . modsys@yandex.ru
https://googledrive.com/host/0BwnV2Ac6zvhMalpOVGktQ1Jic1U
Вы удивитесь, но для такого вроде бы элементарного физического явления, как эффект Доплера в общем виде, а не для частного случая продольного эффекта, который рассмотрел сам Доплер, известно более десяти формул (Лоренца, Эйнштейна, Шредингера, Блохинцева, Замятина и других). И это при том, что в большинстве случаев мы сами создаем передаваемый сигнал и сами же его фиксируем. Поэтому, я надеюсь, Вы понимаете насколько сложно описать те явления, где мы являемся только сторонними наблюдателями, как, например, с гравитацией, где мы примерно так же, как и Аристотель, можем только наблюдать, что тяжелые предметы падают быстрее, чем легкие, и делать из этого свои выводы. Вот поэтому у меня и возникает столько проблем в цикле статей "Скорость гравитации", где я пытаюсь только по данным пассивных наблюдений за планетами Солнечной системы определить скорость гравитации. А пишу я сейчас о гравитации по той простой причине, что именно при рассмотрении гравитационного взаимодействия двух тел у меня получилась формула (1) подобная формуле (3) для эффекта Доплера. Да и сама эта статья является переработанным приложением 2 к статье "Влияние скорости гравитации на смещения параметров орбит планет" [10], которая является 4-ой частью цикла статей "Скорость гравитации".
Но и сам по себе эффект Доплера оказался очень запутанным физическим явлением поэтому и сейчас в Интернете идет активное обсуждение этого вопроса, где наиболее заметными участниками являются Акимов и Купряев. Первый отстаивает свою формулу (упрощенная формула Замятина), а второй пытается доказать справедливость формулы Лоренца. В связи с этим я отдельно остановлюсь и на их работах, хотя они этого и не заслуживают. А результатом моего изучения вопроса по эффекту Доплера стало то, что я предложил еще одну формулу (3) для этого эффекта, которую, как и все мои предшественники, я, конечно же, считаю единственно правильной. А самая известная из всех формул это, конечно же, формула Лоренца (2), хотя быстрее всего автор этой формулы не известен, но ее называют именем Лоренца для определенности. А так же, наверное, и потому, что она соответствует его духу отражения физических явлений, когда учитываются только текущие координаты тел, как, например, в аналогичном расчете взаимодействие зарядов в электродинамике, когда без учета запаздывания потенциалов по координатам надо обязательно использовать еще и силу Лоренца.
В приведенных ниже формулах v0 - частота передатчика на движущемся источнике сигнала, а v - частота сигнала, который распространялся в какой то среде или в вакууме со скоростью с и был принят на движущемся приемнике. При этом b1=V1/c и b2=V2/c, где V1 это скорость приемника сигнала и V2 это скорость источника сигнала, а Q1 и Q2 это углы между этими скоростями и радиус-вектором, соединяющим источник 2 и приемник 1 в текущий момент времени. Эту формулу частенько критикуют за то, что она дает неверные результаты, но если в этой формуле учесть запаздывание по координатам, о котором я писал в [10], то ошибки не будет. Таким образом, надо просто вместо углов Q1 и Q2 использовать углы A1 и A2 между векторами скорости приемника и источника и радиус-вектором распространения сигнала из той точки 2', где был источник, когда сигнал его покинул, в точку 1, где его принял приемник и получим формулу (3). Но для эффекта Доплера существует еще и релятивистская формула Эйнштейна (4), которую он предложил в работе [8], и которая, естественно, принципиально отличается от классических формул.
F(i,k) = Fn(i,k)*(1 – Vk/Vgr) / (1 – Vi/Vgr) (1)
v =v0*(1 – b1*cos(Q1)) / (1 – b2*cos(Q2)) (2)
v =v0*(1 – b1*cos(A1)) / (1 – b2*cos(A2)) (3)
v =v0*(1 – b*cos(Q)) / sqrt(1 – b^2) (4)
v =v0*(1 – b*cos(Q)) * sqrt(1 – b^2) (4')
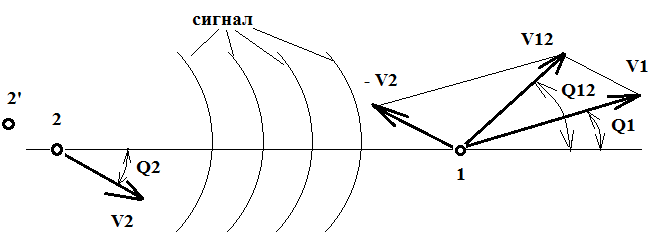
Рис. 1. Схема для расчета эффект Доплера в общем виде.
А т.к. согласно теории относительности не может быть абсолютной скорости и есть только относительные скорости, поэтому формула (2) упрощается в формулу (4) и в ней присутствует только коэффициент b, который равен скорости приемника относительно источника V12 деленной на скорость света. Если использовать только числитель этой формулы, то получающийся результат будет при малых скоростях незначительно отличаться от того, что дает формула Лоренца, естественно, с той же ошибкой, т.к. угол Q12 это угол между вектором скорости приемника относительно источника и радиус-вектором соединяющим источник и приемник в текщий момент времени, а этот угол тоже не учитывает запаздывание по координатам. Но здесь еще появился дополнительный релятивистский множитель, который дает, так называемый, поперечный эффект Доплера, которого нет в классической формуле (2). Одноко, альтернативные ученые пытаются доказать, что такой эффект существует и в их классических формулах для эффекта Доплера. Я же в их формулах, как я покажу ниже, кроме ошибок никакого поперечного эффекта Доплера не нашел. А откуда же он тогда взялся в формуле (4).
Оказывается, эта формула учитывает, согласно СТО, замедление времени при увеличении относительной скорости источника сигнала и в результате уменьшается частота передатчика, расположенного на источнике. Причем, она уменьшается и при движении источника вдоль линии соединяющей источник и приемник и в поперечном направлении, т.е. этот эффект никак не является именно поперечным и здесь надо говорить о другом названии для этого эффекта. И по аналогии с гравитационным красным смещением, которое дает для такого же эффекта Доплера ОТО, его можно назвать скоростным красным смещением СТО, т.к. и там и там этот эффект уменьшения частоты передатчика расположенного на источнике объясняется замедлением времени и эти эффекты не зависят от направления движения источника. Но, как Вы, наверное, уже догадались, формула (4) должна давать не замедление времени, а увеличение, поэтому во многих работах авторы запросто релятивистский множитель переносят из знаменателя, как это было у автора формулы, в числитель и получают волюнтаристским методом формулу (4'), что является принципиальной ошибкой. Ведь Эйнштейн ясно написал, что "Это и есть принцип Доплера для любых скоростей". Правда, перед этим он рассматривал частный случай, когда источник покоится, а приемник движется.
Но в любом случае релятивистская формула для эффекта Доплера явно ошибочна и с методологической точки зрения, т.к. должна отражать оба релятивистских эффекта замедления времени. И, если для гудка паровоза можно пренебречь его массой для учета гравитационного красного смещения ОТО (впрочем, так же как и его скоростью при скоростном красном смещении СТО), то, например, для двойных пульсаров надо точно учитывать оба эффекта [4], а формула (4) учитывает только один эффект замедления времени. Более того, в учебниках по ТО дается и другое объяснение гравитационного красного смещения, которое объясняет сдвиг спектра в красную сторону, т.е. уменьшение частоты излучения, исходя из корпускулярной природы света. Там получается, что фотон, вылетевший из звезды с определенной частотой излучения, при удалении от звезды должен преодолевать действие ее гравитационного поля и поэтому терять часть своей энергии. А, т.к. энергия фотона определяется согласно Планку как h*v, то значит при этом должна уменьшаться и его частота v. Причем эти два объяснения считаются равнозначными (наверное, потому, что результат получается один и тот же), но ведь это два совершенно разных физических эффекта (если их можно назвать физическими) и если оба эти объяснения верны, то учитывать надо оба этих эффекта, т.е. результат от гравитационного красного смещения согласно ОТО должен быть в два раза больше.
Правда, сейчас в академических изданиях, наконец-то, наметилась некоторая дискуссия по этому вопросу и начинают утверждать, что верно только первое объяснение гравитационного красного смещения. А вот автор [9], анализируя эту дискуссию, утверждает, что эти объяснения согласно ТО противоречат друг другу, т.е. получается, что пока еще сами сторонники ТО не знают этой самой ТО. Однако их познания по ТО не мешает им успешно применять самые разнообразные формулы ТО, которые, конечно же, дают результаты, которые успешно подтверждаются экспериментально, как, например, с системой двойного пульсара PSR 1913+16 (см. приложение 4 в [10]). Но ниже, после того, как мы разберемся с классическим эффектом Доплера, я покажу, что релятивистская формула все равно ошибочна и чисто формально, т.к. так же, как и формула для классического общего эффекта Доплера дает результаты, отличающиеся от наблюдаемых данных.
Но откуда же в классическом эффекте Доплера появился поперечный эффект в формуле Акимова, который, как показал анализ литературных источников по эффекту Доплера, привел меня к работе Замятина [1], где как раз формула, которую пропагандирует сейчас Акимов, и получена. Но у Акимова, например, вот этой работе [3], изменяется скорость распространения сигнала (у Замятина она не меняется), и вывод этой формулы у него явно уступает выводу Замятина, хотя он у обоих не правильный. А ошибочность формулы Акимова сейчас активно критикует Купряев [2] и приводит свой вывод общей формулы для эффекта Доплера, который приводит к классической формуле (2). Но все они, не считая мелких ошибок, сделали одну принципиальную ошибку, а именно они совершенно не рассматривают сам передатчик, генерирующий исходную частоту, которую и надо промодулировать этим эффектом по законам частотной модуляции. Давайте рассмотрим их ошибки и начнем с вывода формулы Замятиным, который воспроизведем по рисунку из его же работы.
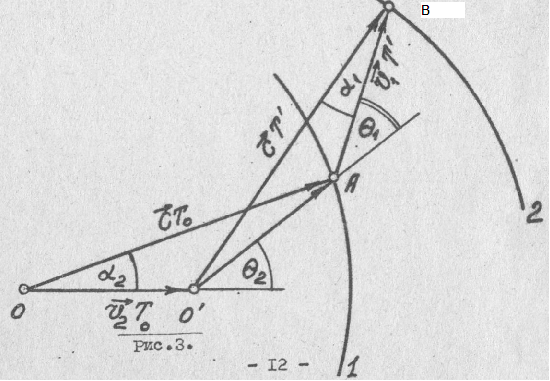
«Пусть движущийся со скоростью V2 источник в точке O создал некоторый фронт волны 1, зафиксированный далее также движущимся со скоростью V1 приемником в точке A в момент времени t1. К этому моменту источник, перейдя в точку O’, создает следующий той же фазы фронт 2, который настигает удаляющийся приемник в точке B в момент t2. Требуется определить период принятых колебаний T’= t2 – t1 и частоту v’.
Из тр-ка O’BA отрезок O’A определится выражением
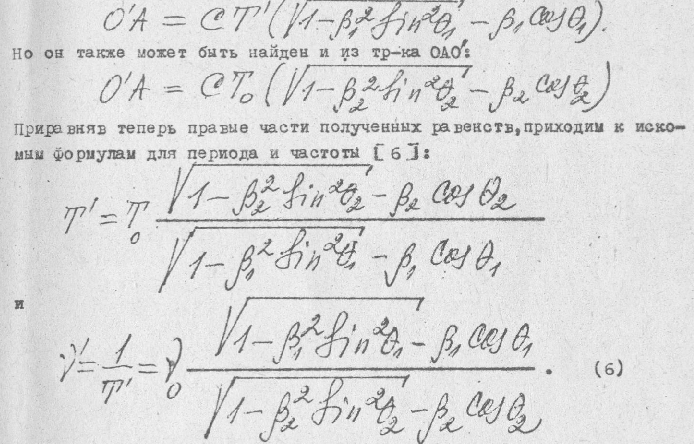
И к этой же самой своей формуле (6*) Замятин приходит и другим путем из формулы продольного эффекта Доплера, полученной самим Доплером
v’ = v0 * (C – V1) / (C – V2) (1*)

Вот только я никак не могу взять в толк какое отношение вывод Замятина (Акимова, Купряева) имеет именно к эффекту Доплера, т.е. к изменению частоты принимаемого движущимся приемником сигнала, который излучается передатчиком на движущемся источнике, т.е. к частотной модуляции. Например, гудок паровоза является передатчиком, который генерирует сигнал с определенной частотой и который потом подвергается частотной модуляции движущимся источником, т.е. паровозом. При приближении паровоза мы слышим сигнал более высокой частоты, а при удалении - более низкой. А все эти авторы вообще ничего не пишут о частоте именно передатчика. У них за исходный сигнал принимается либо движение фронта ударной волны либо уже промодулированный источником сигнал передатчика. Конкретно Замятин рассматривает движение фронта ударной волны. И здесь у него время T и T’ не является никаким периодом колебаний, т.к. это просто время распространения сигнала, которое будет одинаковым и для ударной волны и для обычной волны при любой частоте передатчика, т.е. при любом периоде его колебаний. А у фронта ударной волны, которую создает источник, эта частота может зависеть только от скорости источника, а не формироваться искусственно, как у Замятина, когда новый фронт волны образуется при достижении сигналом приемника. Но его не может быть и у обычной волны передатчика с заданной фазой сигнала, т.к. здесь можно говорить только условно о фронте волны при фазе равной нулю.
Вывод Замятина формулы для якобы эффекта Доплера, можно, наверное, как-то применить для распространения фронта ударных волн с учетом запаздывания сигнала по координатам, но никак не к эффекту Доплера. Но тогда надо и назвать этот эффект, который рассматривает Замятин, например, эффектом Маха, т.к. Мах первым определил формулу для конуса ударных волн при движении пули. Да, формула у Замятина получается вроде бы очень похожая на правду, но ведь и корова тоже очень похожа на быка, но любому человеку ясно, что она не бык. Вот и распространение фронта ударной волны не имеет отношения к эффекту Доплера, т.е. к частотной модуляцией сигнала передатчика и Замятин находит период, фиксируемый на приемнике, между двумя фронтами ударных волн, формируемых самим движущимся источником в строго заданные моменты времени, т.е. тогда, когда фронт первой волны достигнет приемника. Ведь он прямо пишет, что «К этому моменту источник, перейдя в точку O’, создает следующий той же фазы фронт 2, который настигает удаляющийся приемник в точке B в момент t2», что явно не относится к передатчику и ниже я на примере покажу, что фаза именно у передатчика при этом может быть любой.
При этом, странно, что, когда Замятин критически анализирует другие формулы, он пишет «Тот факт, что из всех этих формул вытекает закон продольного эффекта, очевидно, не является достаточным доказательством их правильности. Можно было бы придумать много других формул, которые бы при условии Q1=Q2=0 стали бы сводиться к выражению (1*)». Так почему же он и свою формулу не подверг сомнению по этой же причине. Тем более, как видно из текста, Замятин даже проводил эксперименты по проверке эффекта Доплера. Но, почему же он не провел простейший эксперимент по выявлению различий в результатах, получаемых по разным формулам (результаты сравнения я дам ниже), а занялся сложным экспериментом с вращающимся на диске передатчиком звуковых волн для поиска мифического поперечного эффекта Доплера, который получался в его формуле. А вот, если бы он провел обычные эксперименты для общего эффекта Доплера, то получил бы, как будет показано далее, результаты по своей формуле лучше, чем дает формула Лоренца.
Но, надо отдать должное Замятину. Ведь его формула (6*) действительно просто фантастическая, т.к. она эквивалентна его формуле через углы альфа, один из которых берется для источника из прошлого времени, а другой для приемника из будущего времени. И вот это для меня является фантастикой, т.к. я никак не могу понять, как положение приемника в будущем времени может повлиять на принимаемый им сигнал в настоящем времени. Неужели и здесь процессом распространения волн управляет божественный принцип наименьшего действия, где движение в настоящем времени подчиняется заданному положению в будущем времени. Но, давайте обратимся к конкретному примеру расчета эффекта Доплера по классической формуле Лоренца (2), Юдина (3) и по полученной Замятиным формуле (6*), а потом рассмотрим и выводы Акимова и Купряева. Для этого немного видоизменим рисунок Замятина. Пусть у нас в какой то момент времени в точке О передатчик, который движется на источнике со скоростью V2, начинает генерировать сигнал определенной частоты, например, v0=0,2 Гц с нулевой фазой, который настигает приемник, который движется со скоростью V1, в точке 1. Эта точка находиться на расстоянии 100 м от точки О и ее ордината равна 50 м. Если мы примем, что скорость распространения сигнала с=20 м/с, то, следовательно, с момента, когда была начата генерация сигнала в точке О, прошло времени dt=5 с. Примем, что у нас V1=6 м/с, а V2=10 м/с. А, т.к., когда приемник начал принимать сигнал от передатчика, источник переместился, то в данный момент времени t1 он находится в точке 2.
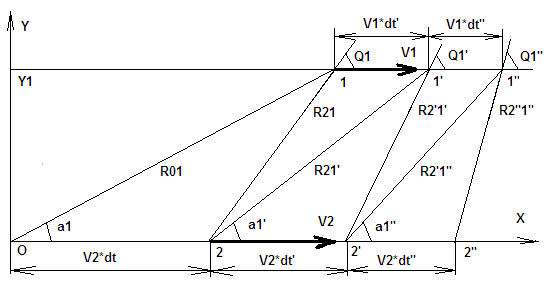
Рис. 2. Иллюстрация к расчету эффекта Доплера по времени распространения фронта волны.
Итак, передатчик будет генерировать колебания с частотой 0,2 Гц, а т.к. эта частота передатчика будет промодулирована (частотная модуляция) движущимся источником, то в направлении на точку 1 сигнал будет распространяться с частотой v(01) = v0 / (1-b2*cos(a1)) = 0,3527 Гц и если бы приемник был неподвижный то именно эту частоту он бы и зафиксировал. А при движущемся приемнике она будет приниматься в точке 1 как частота v(1) = v(01) * (1-b1*cos(a1))= 0,2611 Гц. При этом непосредственно мгновенную частоту принимаемого сигнала в момент, когда приемник будет находиться в точке 1, зафиксировать экспериментально мы не можем, т.к. для этого необходимо иметь хотя бы один период синусоидальных колебаний. Т.е. мы можем зафиксировать частоту только в интервале времени около точки 1, например, начав фиксацию сигнала за пол периода колебаний до момента времени, когда приемник будет в точке 1 и закончив спустя пол периода колебания после этого момента. Например, как это мы видим на рис. 3, если мы приняли часть синусоидальных сигналов S1 и S2 или на участке 1-2 или на участке 2-3 и при этом у нас, естественно, не будет горизонтальной линии, чтобы знать увеличивается амплитуда или уменьшается, то мы, как Вы догадываетесь, не только не сможем определить частоту принимаемого сигнала, но и не сможем сказать у какого сигнала S1 или S2 частота будет больше.
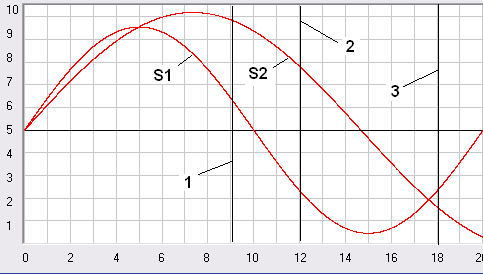
Рис. 3. Сравнение частот двух принимаемых сигналов при их частичном приеме.
При этом для заданной нами в примере частоты колебаний сигнала передатчика v0=0,2 Гц, которая будет приниматься в точке 1 с частотой v(1) = 0,2611 Гц, период которой T(1)= 1/v(1) = 3,83 с, получается очень большая ошибка в определении частоты принимаемого сигнала, т.к. за это время от начала периода и до конца у нас очень сильно изменятся углы a1 и Q1. Но, если мы будем использовать в рассматриваемом примере высокую частоту, чтобы сделать условный период колебаний очень маленьким и максимально уменьшить погрешность, как теоретического, так и практического определения мгновенной частоты, то трудно будет анализировать ошибку использования формул для эффекта Доплера при малых частотах передатчиков. К тому же нам надо сделать наглядным смещение фазы сигнала при рассмотрении вывода формулы Замятиным, поэтому частота и принята мною такой маленькой. А то, что при проведении натурных экспериментов мы никак не можем точно вычислить мгновенную частоту принимаемых сигналов, если у нас изменяются скорости V1 и V2 или углы a1 и Q1, то это данность от которой никуда не уйти. И в таких случаях, говоря о частоте принимаемых сигналов, мы просто всегда должны указывать погрешность, с которой она определена. Но сейчас в нашем примере мы рассматриваем чисто теоретический вопрос, поэтому, и частоту принимаемого сигнала и его фазу мы определяем чисто теоретически. А в этом случае мы уверены, что у нас никаких погрешностей нет, кроме известных нам особенностей времени приема периода сигнала, и мы по данным наших расчетов можем точно сопоставлять результаты, получающиеся по разным формулам.
Так вот, за время dt равное 5 с, сигнал передатчика, выйдя из точки О достигнет точки 1, т.е. в этой точке будет принята нулевая фаза сигнала. А вот сам передатчик за это время, придя в точку 2, сделает ровно одно колебание и у нас в этот момент времени будет начата передача второго сигнала (продолжение первого) с той же нулевой фазой или можно сказать, что будет передан конец первого периода колебаний. Но для следующих моментов времени в точках 2' и 2'' это будет уже не так. До точки 2' передатчик сделает 0,2*(5+3,907)= 1,7814 колебания, а до точки 2'' он сделает 0,2*(5+3,907+3,208)= 2,423 колебания, поэтому утверждение Замятина о том, что в его выводе будет сохраняться фаза передаваемого сигнала, не верно. Да, вообще-то, Замятин и не пишет именно о сигнале. Он кругом говорит о фронте волны, т.е. ведет речь о распространении именно фронта ударной волны, поэтому, не будем больше придираться к его выводу формулы (6*), а давайте просто посмотрим, что она дает.
Для этого, давайте, теперь определим, где будет находиться приемник (точка 1’), когда до него дойдет сигнал из точки 2, где сейчас находится источник, а затем определим, где будет находиться приемник (точка 1’’), когда до него дойдет сигнал от источника из точки 2’. Т.е. давайте повторим на численном примере расчеты Замятина, а для наглядности рассчитаем не одну точку в будущем, как у него, а две. Все эти расчеты можно выполнить и на программе Dopler1, но я их дам здесь в развернутом виде, так, как я их выполнял до написания программы. Для определения времени dt’, которое необходимо для распространения сигнала из точки 2 в точку 1’, составим уравнение
R21’^2 = Y1^2 + (X1 - X2 + V1*dt’)^2
С учетом того, что R21’ = c * dt’, получим квадратное уравнение относительно dt’. Решив его, найдем, что один из корней равен 3,907, т.е. это и будет наше время dt’ за которое приемник переместится из точки 1 в точку 1’, а сигнал от источника из точки 2 настигнет его. Т.к. у нас было X1=86,6 м, а X2=50 м, то мы получим в момент времени t2 следующие координаты приемника и источника
X1’ = X1 + V1* dt’ = 110,04 м
X2’ = X2 + V2* dt’ = 89,07 м
Аналогично произведем расчет и для определения координат точек X1’’ и X2’’ через промежуток времени dt’’ прошедший с момента времени t2. У нас получиться dt’’=3,208 с и координаты приемника и источника станут
X1’’ = X1’ + V1* dt’’ = 129,29 м
X2’’ = X2’ + V2* dt’’ = 121,15 м
Давайте, теперь сравним результаты, получающиеся по формуле Лоренца (2), Юдина (3) и по формуле Замятина (6*). Для этого нам потребуются для формулы (2) углы Q1, а для формулы (3) углы а1 и для формулы (6*) тоже углы Q1.
a1 = arctg (Y1 / X1) = 30
a1’ = arctg (Y1 / (X1’ – X2)) = 39,79
a1’’ = arctg (Y1 / (X1’’ – X2’)) = 51,19
Q1 = arctg (Y1 / (X1 – X2)) = 53,8
Q1’ = arctg (Y1 / (X1’ – X2’)) = 67,25
Q1’’ = arctg (Y1 / (X1’’ – X2’’)) = 80,79
По формуле Юдина (3), с учетом наших обозначений и того, что b1= V1/c , b2= V2/c и т.к. скорости источника и приемника параллельны, то углы между векторами этих скоростей и радиус вектором для источника и приемника будут одинаковые, частота сигнала, принимаемого приемником, когда он будет находиться в точках 1, 1’ и 1’’, будет
v1 = v0 * (1 – b1 * cos(a1)) / (1 – b2 * cos(a1)) = 1,3055 * v0
v1’ = v0 * (1 – b1 * cos(a1’)) / (1 – b2 * cos(a1’)) = 1,2496 * v0
v1’’ = v0 * (1 – b1 * cos(a1’’)) / (1 – b2 * cos(a1’’)) = 1,1825 * v0
А по формуле Лоренца (2) мы получим
v1 = v0 * (1 – b1 * cos(Q1)) / (1 – b2 * cos(Q1)) = 1,1676 * v0
v1’ = v0 * (1 – b1 * cos(Q1’)) / (1 – b2 * cos(Q1’)) = 1,0959 * v0
v1’’ = v0 * (1 – b1 * cos(Q1’’)) / (1 – b2 * cos(Q1’’)) = 1,0348 * v0
И по формуле Замятина
v1= v0 * sqrt(1–b1^2*sin(Q1)^2)–b1*cos(Q1)) / sqrt(1–b2^2*sin(Q1)^2)–b2*cos(Q1))= 1,2798*v0
v1’= v0 * sqrt(1–b1^2*sin(Q1’)^2)–b1*cos(Q1’)) / sqrt(1–b2^2*sin(Q1’)^2)–b2*cos(Q1’))= 1,2177*v0
v1’’= v0 * sqrt(1–b1^2*sin(Q1’’)^2)–b1*cos(Q1’’)) / sqrt(1–b2^2*sin(Q1’’)^2)–b2*cos(Q1’’))= 1,1491*v0
Интересно отметить, что по формулам Замятина через углы a1, т.е. когда для текущего времени приемника вычисляется принимаемая им частота по углам, отражающим положение источника в прошлом времени, т.е. учитывается запаздывание по координатам, а положение приемника в будущем времени, получаются те же результаты, как и по его формуле (6*), когда углы и для приемника и для источника вычислялись нами выше по их положению в текущий момент времени.
v1= v0 * sqrt(1 – 2*b1*cos(a1’)^2) + b1^2) / sqrt(1 – 2*b2*cos(a1) + b2^2)= 1,2799*v0
v1’= v0 * sqrt(1 – 2*b1*cos(a1’’)^2) + b1^2) / sqrt(1 – 2*b2*cos(a1’) + b2^2)= 1,2176*v0
Таким образом, мы видим, что при принятых нами значениях скоростей, результаты по разным формулам получаются существенно разными и эту разницу в полученных нами данных легко зафиксировать в простейшем эксперименте. Ведь, если увеличить наши скорости из примера в 15 раз, то мы получим данные для эксперимента с распространением звука, а осуществить такой эксперимент при существующем уровне развития техники не составляет никакой трудности, в отличие от эксперимента Айвиса и Стилуэлла с электромагнитным излучением для выявления замедления времени, где разница в смещении линий спектра излучения атомов будет на пределе чувствительности приборов. Поэтому, мне не понятны нескончаемые споры в последнее время о том, какая из этих двух формул (Лоренца или Замятина) правильная для эффекта Доплера (естественно моя формула, т.е. Юдина). При этом, формула Замятина, хоть и похожа на формулу для эффекта Доплера, но ее вывод, сделанный Замятиным, говорит о том, что она получена явно для другого эффекта. Но, давайте до проведения натурных экспериментов, проверим формулы Лоренца, Юдина и Замятина по данным нашего вычислительного эксперимента.
Так вот, как я писал выше, когда источник был в точке О, передатчик начал излучать сигнал с частотой 0,2 Гц и через 5 с, когда источник прибывал в точку 2, передатчик сделав одно колебание опять начинал излучать сигнал для следующего периода колебаний. А приемник начал принимать сигнал от первого периода колебаний в точке 1 и закончил принимать в точке 1', а между этими двумя положениями приемника прошло время dt’= 3,907 с, т.е. на этом интервале времени частота принимаемого сигнала получится v(11')= 1/3,907= 0,2559 Гц. Давайте теперь посмотрим какая частота на этом интервале времени, т.е., грубо говоря, в точке расположенной посередине между точками 1 и 1' получается по данным, которые мы получили выше, по нашим трем формулам, если ее вычислить как среднюю частоту между частотами рассчитанными для точек 1 и 1' и сравним ее с наблюдаемым значением 0,2559 Гц.
v(11')= 0,2*(1,3055+1,2496)/2= 0,2555 Гц (Юдин)
v(11')= 0,2*(1,1676+1,0959)/2= 0,2264 Гц (Лоренц)
v(11')= 0,2*(1,2798+1,2177)/2= 0,2498 Гц (Замятин)
Как видим, формула Лоренца дает очень плохой результат, а формула Замятина, хотя и получена не для эффекта Доплера, но дает результат гораздо лучше. Но почти идеальный результат получается только по формуле Юдина и, таким образом, вопрос о том, какая формула для общего эффекта Доплера является правильной можно считать закрытым, а ниже я приведу более обширные данные как для рассмотренного нами случая, так и для звука и света, которые тоже подтверждают именно мою формулу. Но выше я упомянул еще о двух выводах формул для эффекта Доплера – Акимова и Купряева, одна из которых повторяет формулу Замятина, а другая формулу Лоренца, но они получены только для неподвижного приемника и поэтому менее ценны, чем общие формулы Замятина (6*) и Лоренца (2). Но давайте рассмотрим и то, как эти авторы получили их, т.к. возможно, что они их выводили действительно для эффекта Доплера, в отличие от Замятина, и тогда интересно будет посмотреть откуда у них получаются хоть и разные результаты, но оба не верные. А начнем в исторической последовательности с Акимова. В своей работе [3] он пишет
«На рис. 1а вычерчен застывший в произвольный момент динамический процесс распространения волн. На одной из окружностей — неважно какой, поскольку все треугольники 0АВ будут подобными, — выбрана точка А. Стороны треугольника 0А и 0В соответствуют скоростям v и c; нужно по двум сторонам треугольника 0АВ найти третью — АВ. Для решения этой задачи треугольник 0АВ достраиваем до прямоугольного 0АС, как показано на рис. 1б. Из последнего чертежа находим отрезки a = v sin θ и b = v cos θ. По теореме Пифагора составляем равенство:
![]()
Если в последнее выражение подставить значения a и b, получим искомую скорость c' :
![]() .
(3)
.
(3)
Умножая обе части равенства (3) на период колебаний Т, получаем изменившуюся за счет эффекта Доплера длину волны λ', которую удобно выразить через параметр β:
![]() . (4)
. (4)
Формула (4) есть истинное, абсолютно точное выражение, описывающее эффект Доплера для любых значений параметра β.» (здесь у автора β= v/c).
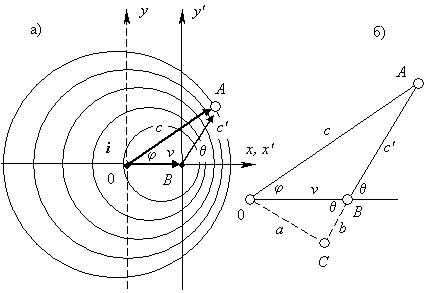
Рис. 4. Чертеж (а) представляет собой застывшее изображение процесса распространения волн при движущемся источнике колебаний ( i ). Пока волновой фронт, испущенный из точки 0, дойдет до точки А, источник колебаний i окажется в точке В. Чтобы найти выражения для векторной суммы векторов v и c, на чертеже (б) показан вспомогательный прямоугольный треугольник. Воспроизведено из работы [3], где это рис. 1.
Да формула у Акимова получилась та же самая, что и у Замятина (для неподвижного приемника), но в выводе у Замятина хотя бы скорость распространения сигнала была одинаковой во всех направлениях, а у Акимова явно видно, что вывод притянут за уши, т.к. у него, почему то, скорости c и c’ разные, хотя он пишет в подписи к рисунку, что, как и Замятин, рассматривает движение волнового фронта. Но у этого фронта при распространении в какой-то среде может быть только одна скорость распространения, а не разные в разных направлениях при отсутствии движения среды. К тому же, у Акимова мы видим и еще один математический фокус, т.к. в завуалированном виде Акимов здесь демонстрирует в действии ту же фантастическую машину времени, что и Замятин. Ведь скорости c и V у него относятся к настоящему времени, а скорость c’ к будущему времени. Да, чисто с математической точки зрения сложение векторов выполнено правильно, но в нашем случае эти вектора нельзя складывать, т.к. у нас это не отвлеченные вектора, а векторы конкретных скоростей. А в таком случае мы можем складывать векторно скорости тела движущегося одновременно по двум координатам, чтобы найти суммарный вектор скорости, который позволит вычислить координаты точки, куда придет тело за то же время, что и двигаясь отдельно по каждой из координат, т.е. мы рассматриваем движение в одном и том же времени. А у Акимова получается, что из точки В в точку А тело (фронт волны) движется уже в будущем времени, когда движение со скоростями c и V уже закончилось, т.е. ни о каком векторном сложении скоростей тут не может быть и речи.
И его утверждение о том, что частота v0 (у него используется эквивалентная ей длина волны λ) является частотой передатчика, которая с учетом эффекта Доплера по его формуле, учитывающей движение источника сигнала, получается для приемника другой, тоже является ошибочным. Ведь у Акимова за v0 берется частота сигнала при его движении из точки 0 в точку А (то же самое и у Купряева), но это не частота передатчика, которая должна согласно эффекту Доплера при движении источника сигнала приниматься на приемнике уже другой величиной. Это частота сигнала, распространяющегося в направлении на приемник, т.е. из точки 0 в точку А, которая является частотой сигнала передатчика уже промодулированной движением источника и определится она согласно формуле Доплера как v(0А) = v0 / (1-V*cos(Q)/c). И в том случае, если у нас приемник неподвижен, то он эту частоту и будет принимать. А, если говорить о формуле Акимова (4*), то этой частоте у него соответствует длина волны λ, но у Акимова она, почему-то, считается исходной частотой передатчика, которую надо опять подвергнуть преобразованиям согласно его формуле, т.е. промодулировать еще раз. Но в таком случае я вообще затрудняюсь сказать, что он определяет как λ'. Таким образом, вывод формулы для эффекта Доплера у Акимова не только не имеет никакого отношения к эффекту Доплера, но и выполнен, мягко говоря, антинаучными методами.
А теперь давайте посмотрим, что же придумал Купряев, чтобы защитить от Акимова (Замятина) формулу Лоренца. Проанализируем только начало его вывода формулы для эффекта Доплера, т.к. ясно, что дальше нечего и смотреть. В работе [2] Купряев пишет
«Излучаемые источником сферические волны распространяются в пространстве со скоростью света c. Какой период tau “колебания” волн зафиксирует неподвижный наблюдатель P ?
Обозначим через Q угол между направлением распространения волны и положительной осью X в системе отсчета S. Пусть начало колебания источника, приходится на момент времени t=0, когда источник находится в начале координат системы отсчета S. После завершения полного цикла колебания (периода T), источник переместится в точку с координатами (VT,0,0) и начинает излучать вторую волну. Волны, разделенные промежутком времени T и расстоянием VT, будут, таким образом, распространяться в неподвижном пространстве как две расширяющиеся сферы: с центром в начале координат (0,0,0) и с центром в точке с координатами (VT,0,0). Дальнейшая судьба источника нас не интересует.
Пусть первая волна, испущенная источником в момент времени t=0, достигает наблюдателя в момент времени NT в точке с координатами (N*c*T*cosQ, 0, N*c*T*sinQ), где N – число длин волн (необязательно целых), укладываемых на этом расстоянии. (Источник к этому моменту времени может находиться где угодно, например, на расстоянии NVT от начала координат S и совершенно не интересует.) Радиус первой волны (с центром в начале координат (0,0,0)) в момент времени NT составляет NcT.
Вторая волна, испущенная источником в момент времени t=T, очевидно, имеет радиус (N-1)*c*T с центром в точке с координатами (VT,0,0) и достигает наблюдателя в момент времени NT+tau. Радиус второй волны увеличивается при этом на величину c*tau. Нужно найти tau.»
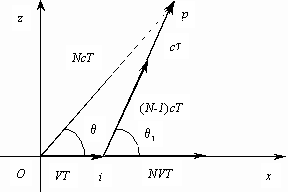
Рис. 5. Схема к расчету эффекта Доплера при неподвижном приемнике Р и движущимся со скоростью V источнике. Воспроизведено из работы [2].
Тут мы видим, что Купряев не стал совершать ошибку Замятина и вычислять время движения первого фронта мифической волны до приемника, чтобы через это время началось распространение второго фронта или Акимова, у которого используется мифическая скорость с’ для движения второго фронта волны, а рассматривает движение второго фронта волны ровно после одного колебания с той же скоростью. Только использует при этом не период колебания передатчика, как надо было сделать, а использует период уже промодулированного сигнала. А вот дальше опять начинается фантастика с машиной времени, но не явная, как у Замятина и Акимова, а в виде утверждения Купряева о том, что расстояние между точками i и Р у нас будет (N-1)*c*T + tau*с. Уж хоть бы написал, что на время tau увеличится период N колебаний, и то было бы больше похоже на правду. Но, нам на этом пути движения волны не известны ни период колебания этих волн, ни количество волн, которое уложится на этом отрезке, и по этому здесь нет никакого решения. А вот при гипотезе Купряева о том, что у нас между точками О и Р и точками i и Р будет одинаковое количество колебаний, но с разным набором длин волн есть решение, но оно является полным произволом.
При этом если бы речь у нас шла о теоретическом выводе какого-то закона, который потом мы будем экспериментально проверять по эффектам, которые следуют из этого закона, то в данном случае возможны различные гипотезы. А здесь у нас рассматривается теоретическое доказательство справедливости уже существующего закона для расчета эффекта Доплера, поэтому, мы можем использовать только бесспорные утверждения. А в данном случае за время tau при разных частоте передатчика, скорости источника и угле Q у нас может быть произвольное количество колебаний. Единственный случай, который здесь мог бы представлять интересен это когда между точками O и P будет укладываться одна длина волны, т.е. при N=1. Тогда у нас расстояние между вторым положением источника и приемника будет (N-1)*c*T + tau*с =0 + tau*с, но в этом случае нельзя принять, что Q1=Q, т.к. это можно сделать только при очень больших N. Да и в этом случае предположение, что за время tau будет сделано одно колебание тоже будет ошибочным. Поэтому, весь вывод Купряева построенный на его фантастическом утверждении является ошибочным и дальше можно не читать, т.к. там пошла голая математика, где он подобно тому, как мы находили dt в численном примере рассматривая формулу Замятина, находит tau, а потом, используя ее, находит выражение для частоты принимаемого сигнала (формула 12*), которую умножает и делит на бесконечность и получает формулу Лоренца.
Давайте лучше, используя эту формулу Лоренца, которой должны соответствовать все преобразования Купряева, проверим его фантастическое заявление. Для этого используем данные нашего численного расчета на рис 2. У нас там было ОР=100 м, с=20 м/с, V=10 м/с, Q=30 градусов, XP=86,6 м, а YP=50 м. А вот частоту давайте возьмем побольше, чтобы N не было равно 1. Пусть частота сигнала распространяющегося из точки О в точку Р будет v(0P)=1 Гц. Тогда N=100/20/1=5, а частота передатчика (согласно формуле Лоренца) будет v0 = v(0P) * (1 – V * cos(Q)/c) = 0,567 Гц. Теперь найдем угол Q1 и расстояние между точками i и P. Q1=arctg(50/76)=33,13 градуса. iP=YP/sinQ1=91,48 м. А теперь, используя заявление Купряева, найдем tau=(iP – (N-1)*T*c) / c = 0,57 с. Далее найдем (согласно формуле Лоренца) частоту сигнала, который будет распространяться от передатчика из точки i в точку P, т.е. v(iP) = v0 / (1 – V * cos(Q1)/c) = 0,975 Гц. Следовательно, период колебаний этого сигнала будет T(iP)= 1/v(iP)= 1,025 с, что никак не соответствует заявлению Купрява о том, что он будет равен tau, т.е. 0,57 с. Но, если бы даже он сделал более правдоподобное заявление, что на время tau увеличится период N колебаний, то и тогда ответ бы был не правильным, т.к. тогда T(iP)= ((N-1)*T(OP)+tau)/N = 0,915, что тоже не равно 1,025. Да, далее Купряев пишет, что углы Q и Q1 будут примерно равны при очень больших N, но как бы не было велико N, его заявление всегда будет оставаться ошибочным, кроме случая, когда N равно бесконечности, т.е. когда период колебаний будет равен нулю и не будет вообще никаких колебаний, а будет только деление бесконечности на бесконечность и бесконечная благодать.
Но, если бы даже Купряев правильно определил отношение периодов принимаемого сигнала при его движении из точки О и из точки i, то и в этом случае эффект Доплера у него был бы рассчитан не правильно из за той же ошибки, что была у Акимова. Ведь в эффекте Доплера нам надо найти изменение частоты именно передатчика, но Купряев, зачем-то, используя преобразования Галилея, находит частоту источника в движущейся системе отсчета и приходит к выводу, что она будет такой же, как и в покоящейся системе координат. Но, это частота самого передатчика при этом не изменится, а частота волн распространяющихся в разных направлениях из-за частотной модуляции при движении источника будет разной. А он, как и Акимов, дает формулу для вычисления величины на которую изменится период сигнала передатчика, уже промодулированный движением источника при его распространении из точки О, по сравнению с периодом сигнала передатчика, промодулированного движением источника, при его распространении из точки i.
А вот если бы Акимов и Купряев ясно себе представляли, что эффект Доплера это частотная модуляция сигнала передатчика движущимся источником с последующей частотной модуляцией этого (уже промодулированного источником) сигнала еще и приемником, то они не сделали бы этой ошибки, а именно – не принимали бы за исходный сигнал передатчика сигнал уже промодулированный источником. А Купряев ясно пишет, что у него период T= Ti, т.е. он тоже принимает, что из точки О в точку P у него сигнал распространяется именно с частотой передатчика, но на самом деле из точки О в точку P будут распространяться волны с частотой v(ОP) = v0 / (1 – V*cosQ/c), а не с частотой передатчика, которая будет v0. Таким образом, период этих колебаний будет не 1/v0, а 1/v(ОP) и, следовательно, вторая волна у него начнет распространяться из точки i, когда передатчик с частотой v0 еще не успеет сделать целое колебание. Более того, т.к. у него получилась формула для частоты сигнала принимаемого из точки i в функции от частоты сигнала принимаемого из точки О, то его формула в функции от частоты передатчика должна выглядеть так, как дано ниже, а это точно не формула Лоренца (2), где v0 это именно частота передатчика. И получается, что и Купряев зачем то, как и Акимов, опять подверг преобразованиям (согласно формуле Лоренца) частоту сигнала распространяющегося из точки О в точку P.
v(iP) = v(ОP) * (1 – V * cos(Q)/c) = v0 * (1 – V * cos(Q)/c)^2
Ну, а теперь давайте вернемся к формуле Эйнштейна и потом проверим все эти формулы по данным вычислительных экспериментов, которые проведем на программе Dopler2, где я по сравнению с программой Dopler1, убрал расчеты по формуле Замятина и добавил расчеты по формуле Эйнштейна. Так вот, что касается этой формулы. Здесь, чтобы говорить о замедлении темпа течения времени, надо определиться относительно чего мы будем фиксировать это замедление, т.е. нам нужно какое-то эталонное время. И здесь утверждение СТО о том, что все системы отсчета равноправны, нам ничего не дает, т.к. нам надо рассмотреть два варианта замедления времени относительно его эталонного значения. Вот в ОТО, например, с замедлением времени все понятно и оно определяется относительно темпа течения времени вдали от гравитирующих масс, т.е. за эталонное значение принимается темп течения времени, когда полностью отсутствует этот эффект. Очевидно, и при рассмотрении нашей задачи нам надо задаться эталонным течением времени, когда полностью отсутствует этот эффект, т.е. в абсолютно неподвижной системе отсчета (АСО). А в таком случае у нас получается, что формула (4') дает явно абсурдный результат (не говоря уже о том, что формула (4) вообще противоречит утверждению о замедлении времени на источнике сигнала). Давайте рассмотрим два варианта вычислений по формуле (4') изменения частоты принимаемых на приемнике сигналов от передатчика, расположенного на источнике, когда этот эталонный передатчик, покоясь в АСО, т.е. при эталонном темпе течения времени, генерирует сигналы с частотой 1 Гц.
Первый вариант. Приемник покоится в АСО, а передатчик движется перпендикулярно радиус-вектору соединяющему их (продольный эффект Доплера отсутствует) со скоростью 0,866*с, что дает значение релятивистского множителя 0,5. В эталонном времени передатчик сделает за 10 с 10 колебаний, но, т.к. темп течения времени на источнике будет в 2 раза меньше, то за этих 10 эталонных секунд передатчик сделает только 5 колебаний, что мы и зарегистрируем на приемнике в эталонном времени, т.е. все согласно формуле (4'). А теперь давайте во втором варианте примем, что это у нас источник покоится в АСО, а приемник движется со скоростью 0,866*с. Таким образом, передатчик за 10 эталонных секунд и сделает 10 колебаний, но, т.к. темп течения времени на приемнике будет в 2 раза меньше темпа течения эталонного времени, то мы на приемнике зарегистрируем эти 10 колебаний за 5 секунд и получится, что частота принимаемых сигналов не уменьшится в 2 раза, а наоборот увеличится. И здесь мы видим полную абсурдность формулы (4'), где используется относительная скорость в релятивистском множителе. Естественно, эти же рассуждения можно применить и к формуле (4). Поэтому, если и пользоваться формулой Эйнштейна для учета замедления темпа течения времени, то формулой (4) при покоящемся источнике, а формулой (4') при покоящемся приемнике, но это противоречит принципу относительности, т.к. здесь требуется АСО, чтобы узнать, какой формулой пользоваться.
Хотя, если мы рассмотрим вопрос замедления темпа течения времени в ОТО, то там все будет логично. Передатчик, находящийся на массивном источнике, будет генерировать частоту меньше чем 1 Гц и мы это зафиксируем на Земле, которая, будем считать, практически не создает гравитационного поля сопоставимого с полем создаваемым на источнике, как гравитационное красное смещение. А, если передатчик будет находиться на Земле и будет генерировать частоту 1 Гц, а мы будем фиксировать эти сигналы на массивном приемнике, где будет замедление темпа течения времени, то мы зафиксируем частоту больше 1 Гц, т.е. зафиксируем гравитационное синее смещение. Аналогичные результаты мы получим и в том случае, если будем интерпретировать эффект смещения спектров излучения атомов в красную сторону при нахождении атомов на массивных телах с использованием эффекта покраснения фотонов, т.к. при приближении к массивному телу фотоны будут не терять энергию, как при вылете от массивного тела, а наоборот увеличивать свою энергию. А, т.к. их энергия определяется согласно формуле Планка, как h*v, то при неизменной величине h у нас будет возрастать их частота и, следовательно, мы будем также наблюдать смещение спектров излучения в синюю сторону.
Вообще-то, как я постоянно пишу, все эти эффекты с замедлением времени я считаю фокусами Эйнштейна, но, т.к. мы анализируем его формулу, то приходится это делать по его правилам. А здесь мы видим, что в этих правилах что-то не ладно и формулы (4) и (4'), где присутствует релятивистский множитель ответственный за замедление времени, являются явно ошибочными. Да и экспериментальное подтверждение замедления времени от скорости в поперечном эффекте Доплера сделанное в 1938 году Айвисом и Стилуэллом не убедительно, т.к. эксперимент, проведенный в 1989 году Победоносцевым, Крамаровским и Паршиным, не подтвердил в этом эксперименте замедления времени. Но даже, если этот эффект и существует и мы будем в формуле (4') учитывать только замедление темпа течения времени на источнике, движущимся относительно приемника, то не понятно почему мы в этой формуле не учитываем замедление времени согласно ОТО. И по аналогии с гравитационным красным смещением, которое дает ОТО, поперечный эффект Доплера можно было бы назвать скоростным красным смещением согласно СТО, т.к. и там и там этот эффект уменьшения частоты передатчика расположенного на источнике объясняется замедлением времени и оба этих эффекта не зависят от направления движения источника. А, т.к. последнее, т.е. именно разность скоростей вдоль линии соединяющей источник и приемник, является краеугольным камнем эффекта Доплера, то оба этих эффекта от замедления времени не имеют прямого отношения именно к эффекту Доплера.
И именно такой подход на практике мы и наблюдаем у релятивистов, когда они замедление времени прихода импульсов от двойных пульсаров учитывают как сумму двух замедлений времени, т.е. от гравитационного красного смещения, которое дает ОТО, и от поперечного эффекта Доплера, который дает СТО, (см. формулу (9*) в приложении 4 и графики на рис. 31, 32 и 34 в работе [10]), а релятивистский множитель в формуле (4') не учитывают, когда по частоте принимаемых от пульсара сигналов находят относительную скорость пульсара. Таким образом, мы и здесь видим, что поперечный эффект Доплера не имеет никакого отношения именно к эффекту Доплера, да и само экспериментальное подтверждение этого эффекта, т.е. эффекта замедления времени, проводилось в 1938 году Айвисом и Стилуэллом при наблюдении продольного эффекта Доплера, т.к. экспериментально наблюдать этот эффект именно при движении приемника перпендикулярно источнику практически не возможно. Таким образом, надо сделать однозначный вывод о том, что де факто поперечный эффект Доплера является просто мифом СТО и, говоря именно об эффекте Доплера, надо всегда понимать его именно в классической трактовке, где этот эффект отсутствует.
Об отсутствии этого эффекта говорят и авторы работы [6], которые проанализировали и множество других экспериментальных данных, где различные исследователи пытались доказать наличие этого эффекта. Конкретно они пишут
Считается, что экспериментальным подтверждением наличия сжатия времени в движущейся
системе, а, следовательно, и справедливости всей теории относительности, является эксперимент Г.Айвса и Д. Стилуэлла, выполненный в 1938 г., и якобы косвенно подтверждающий наличие
"поперечного" эффекта Доплера.
Суть эксперимента сводилась к следующему. Измерялись смещения частоты света от движущегося пучка атомов водорода с двух его концов по направлению скорости пучка и против.
По этим смещениям находилась зависимость средней длины волны jт скорости атомов. По характеру зависимости делался вывод о наличии "поперечного" эффекта Доплера.
Однако, не трудно заметить, что экспериментаторы наблюдали смещения частоты, вызванные
тем, что атомы в сфокусированном пучке из-за действия кулоновских сил, а также разных углов вылета атомов из протонной пушки, летят не по прямой, а по кривой (ломанной) линии, а это приводит к смещению частоты в красную сторону. При неизменных условиях фокусировки пучка значение средней длины волны зависит от скорости атомов. Что и наблюдалось в эксперименте.
Никакого подтверждения существования "поперечного" эффекта Доплера в этом эксперименте нет.
Хотя экспериментальные данные, приведенные в работе [7], на которые указывает и автор работы [5], говорят вроде бы о том, что релятивистский множитель в формуле для продольного эффекта Доплера должен присутствовать, но на этом я остановлюсь ниже. А сейчас давайте посмотрим, какие результаты покажут различные формулы для эффекта Доплера в вычислительных экспериментах для условного сигнала и потом для звука и света. Вычислительные эксперименты будем проводить на программе Dopler2, где рассмотрим движение источника и приемника так, как это изображено на рис. 6, но при этом рассмотрим не распространение искусственных ударных волн Замятина, как на рис. 2, а распространение обычных волн генерируемых с заданной частотой v0 передатчиком. Конкретно на рис. 6 v0=0,2 Гц и за один условный период T00=5 с, который используется в расчетах для начала передачи сигнала в начале каждого периода колебаний передатчика, он делает одно целое колебание. А мы в тот момент времени, когда сигнал достигает движущегося приемника, фиксируем время и потом находим промежутки времени между этими соседними зафиксированными моментами времени, т.е. определяем наблюдаемый период принимаемого сигнала.
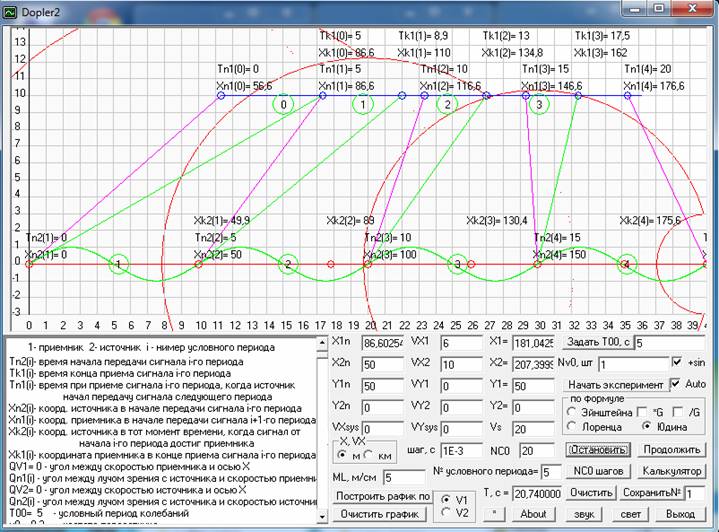
Рис. 6. Вычислительный эксперимент по распространению волн от движущегося источника 2 и принимаемых движущимся приемником 1. В зеленых кружках указаны номера условных периодов между моментами времени, когда передатчик сделал одно колебание и приемник принял сигналы от этого колебания. Скриншот программы Dopler2.
А по различным формулам для эффекта Доплера мы можем определить частоту принимаемого сигнала только в конкретных положениях приемника, поэтому мы находим эту частоту в начале приема условного периода и в конце, а потом находим среднее значение для этого условного периода и сравниваем с наблюдаемым значением, полученным по разности времени прихода сигнала . И ниже в табл. 1 я привожу данные, которые получились при исходных данных заданных на рис. 6. При этом для данных, рассчитанных по формуле Эйнштейна, я сначала привожу значения, которые получаются по его формуле без релятивистского множителя, а потом умноженными на этот множитель и деленными. Как видим, совпадение наблюдаемых данных с расчетными имеется только при расчете по моей формуле, а все остальные дают очень большую ошибку.
Табл. 1. Наблюдаемые и расчетные данные при распространении отвлеченного сигнала.
|
№ периода |
наблюдения |
Юдин |
Лоренц |
Эйнштейн |
Эйнштейн*G |
Эйнштейн /G |
|
1 |
0,256 |
0,256 |
0,224 |
0,218 |
0,214 |
0,223 |
|
2 |
0,242 |
0,241 |
0,206 |
0,205 |
0,201 |
0,209 |
|
3 |
0,221 |
0,221 |
0,192 |
0,190 |
0,186 |
0,194 |
|
4 |
0,201 |
0,202 |
0,183 |
0,178 |
0,175 |
0,182 |
|
5 |
0,189 |
0,189 |
0,179 |
0,171 |
0,168 |
0,175 |
Такой же вычислительный эксперимент проведем и для распространения звуковых волн, а, т.к. звук это волны с частотой 17-20000 Гц, то примем для вычислительного эксперимента v0=10000 Гц. Все остальные данные заданы, так как показано на скриншоте программы на рис. 7, а полученные результаты приведены в табл. 2. Как видим, и здесь совпадение наблюдаемых данных с расчетными имеется только при расчете по моей формуле, а все остальные дают очень большую ошибку.
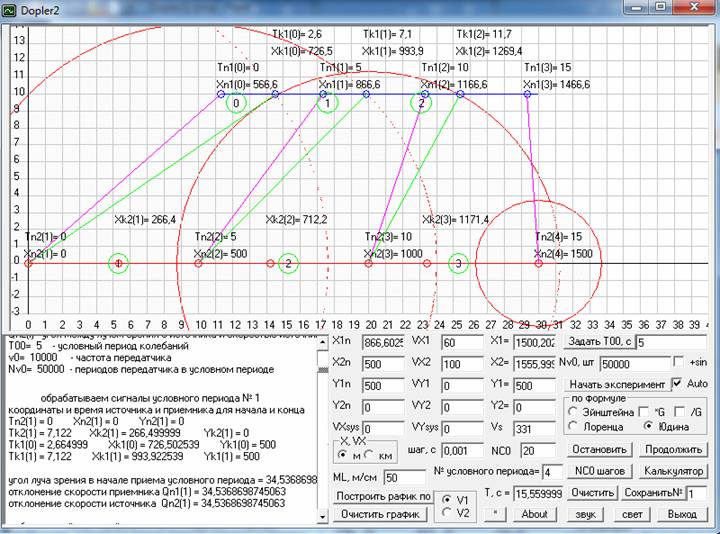
Рис. 7. Вычислительный эксперимент по распространению звуковых волн от движущегося источника 2 и принимаемых движущимся приемником 1. Скриншот программы Dopler2.
Табл. 2. Наблюдаемые и расчетные данные при распространении звукового сигнала.
|
№ периода |
наблюдения |
Юдин |
Лоренц |
Эйнштейн |
Эйнштейн*G |
Эйнштейн /G |
|
1 |
11208,3 |
11201,8 |
10646,2 |
10548,3 |
10471,0 |
10626,2 |
|
2 |
10888,5 |
10873,7 |
10171,7 |
10150,7 |
10076,3 |
10225,7 |
|
3 |
10403,7 |
10406,5 |
9733,9 |
9704,2 |
9633,0 |
9775,8 |
|
4 |
9904,9 |
9921,9 |
9443,0 |
9348,7 |
9280,1 |
9417,7 |
|
5 |
9552,9 |
9567,1 |
9286,3 |
9130,0 |
9063,1 |
9197,4 |
Теперь тот же вычислительный эксперимент проведем и с распространением света, а, т.к. свет это волны с частотой 3,9-7,5 *10^14 Гц, принимаем v0= 5^14 Гц. Все остальные данные заданы, так как показано на скриншоте программы на рис. 8, а полученные результаты приведены в табл. 3. Единственное, что хочу отметить особо, это то, что вследствие большой скорости света решение уравнений, описывающих движение источника и приемника, а так же распространение волн велось здесь с шагом 0,00001 с (для отвлеченных волн на рис. 6 и для звука на рис. 7 было 0,001 с). Как видим, и здесь тот же самый результат и никаких особых свойств у света при применении к нему моей формулы для эффекта Доплера мы не наблюдаем, т.е. утверждение о том, что эффект Доплера для света отличается от этого же эффекта для распространения других волн, не соответствует действительности.
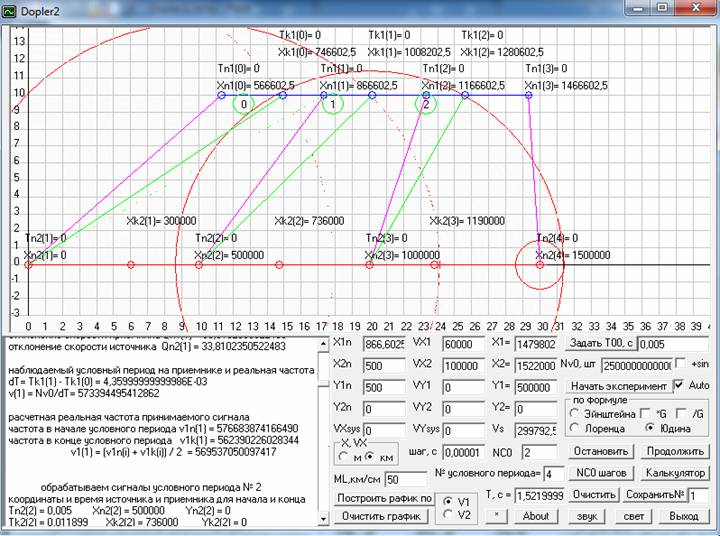
Рис. 8. Вычислительный эксперимент по распространению световых волн от движущегося источника 2 и принимаемых движущимся приемником 1. Скриншот программы Dopler2.
Табл. 3. Наблюдаемые и расчетные данные при распространении светового сигнала.
|
№ периода |
наблюдения |
Юдин |
Лоренц |
Эйнштейн |
Эйнштейн*G |
Эйнштейн /G |
|
1 |
573,4 |
569,5 |
536,4 |
530,3 |
525,5 |
535,1 |
|
2 |
550,7 |
550,7 |
509,6 |
508,3 |
503,8 |
512,9 |
|
3 |
524,1 |
524,1 |
485,5 |
483,7 |
479,3 |
488,0 |
|
4 |
496,0 |
496,8 |
469,7 |
464,0 |
459,9 |
468,2 |
|
5 |
476,2 |
477,1 |
461,3 |
452,0 |
447,9 |
456,0 |
А теперь давайте вернемся к якобы экспериментальному подтверждению формулы Эйнштейна для чисто продольного эффекта Доплера [5,7]. Для этого давайте построим график изменения принимаемой частоты в функции от скорости источника (изменяемой от минус скорости света до плюс скорости света), хотя в экспериментах рассматривали движение лучей источника в обоих направлениях при скорости минус 0,338 и плюс 0,338 скорости света. На рис. 9 Вы видите как изменяется принимаемая частота при ее расчете по двум формулам - моей или Лоренца 3 и 4 и Эйнштейна 1 и 2. Прямая 1 отвечает формуле (4) без релятивистского множителя, а кривая 2 с ним. И кривая 4 отвечает изменению частоты по формулам (2) и (3) при задании скорости источника в покоящейся системе, т.е. в АСО, а кривая (3), если вся система еще и движется со скоростью 0.033 скорости света, что больше предполагаемой скорости всей Солнечной системы, но все же возможно. Напоминаю, что у меня кругом в расчетах положительной считается скорость вдоль луча зрения с источника на приемник. Как видим, хорошее совпадение данных будет и по формуле СТО и по классической формуле (если учесть скорость системы) и таким образом говорить о якобы экспериментальном подтверждении эффекта замедления времени в движущейся системе пока рановато. А при рассмотрении общего эффекта Доплера формула Эйнштейна, как мы видели, совсем не пригодна, даже с учетом замедления времени.
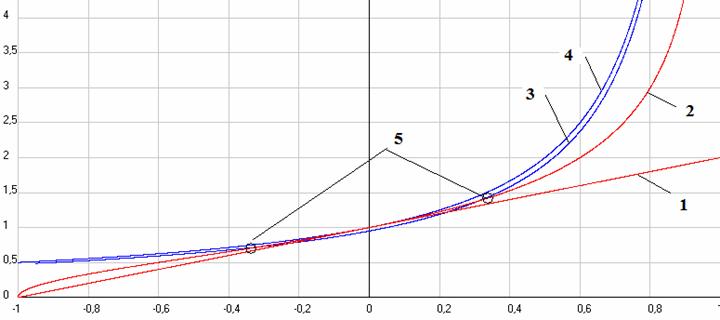
Рис. 9. Изменение принимаемой частоты в долях от исходной при ее расчете по двум формулам - моей или Лоренца 3 и 4 и Эйнштейна 1 и 2 при изменении скорости источника и неподвижном приемнике, а 5 это экспериментальные данные. Скриншот программы Dopler2.
А вывод по этой статье можно сделать такой. Вопрос об эффекте Доплера действительно не такой простой, как могло бы показаться на первый взгляд, т.к. пока очень многие путаются в этом вроде бы элементарном вопросе. А введение в этот эффект еще и поперечного эффекта Доплера еще больше запутало этот вопрос. Но я надеюсь, что мои пояснения позволят Вам разобраться с этим эффектом, а мое уточнение формулы (2), где я предлагаю брать не проекции скоростей источника и приемника на радиус-вектор, соединяющий текущие положения источника и приемника, а на радиус-вектор, соединяющий положение источника сигнала с учетом запаздывания сигнала по координатам, т.е. положение следа источника, и текущее положение приемника, не очень усложнило разбор этого вопроса. Но самое главное это, конечно же, то, что предлагаемая мною формула (3) позволяет получить самый точный результат для общего эффекта Доплера и, таким образом, можно сказать, что это уже окончательная формула для этого эффекта, и других формул (напоминаю, что было их больше десяти) больше не будет и, следовательно, больше не будет путаницы в этом вопросе. А лично я могу больше не беспокоится по поводу того, что я не учел какой-то эффект при выводе формулы для учета динамического давления гравитации из-за того, что у меня получилась формула (1) схожая с формулой (3), и могу спокойно приступать к проведению вычислительных экспериментов по выявлению влияния динамического давления гравитации на смещения параметров орбит планет.
Список литературы
1. – А.Г. Замятин Принцип близкодействия Свердловск, 1988, 153 с. http://yadi.sk/d/mpuZzuId1xkL5
2. – Н.В.Купряев //Классический эффект Доплера// http://www.sciteclibrary.ru/rus/catalog/pages/8803.html
3. – О.Е.Акимов //О формуле, описывающей классический эффект Доплера// http://sceptic-ratio.narod.ru/fi.htm#Doppler
4.- Дж.Х. Тэйлор (мл.) Двойные пульсары и релятивистская гравитация (Нобелевская лекция. Стокгольм, 8 декабря 1993 г.) Успехи физических наук, Июль 1994 г. Том 164, №7
5. - Н.М. Акельев //СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ А. ЭЙНШТЕЙНА – ВЕЛИЧАЙШАЯ АФЕРА В ИСТОРИИ ФИЗИКИ И АЛЬТЕРНАТИВНАЯ ЕЙ КОНЦЕПЦИЯ ЛОРЕНЦА-ФИДЖЕРАЛЬДА-ПЛАНКА // Волгоград, 2013, 166 с http://akelevnm.narod.ru/aboutsto.htm
6 - У.И. Франкфурт, А.М. Френк ОПТИКА ДВИЖУЩИХСЯ ТЕЛ. М.: Наука, 1972 ссылка
7. - C. Novotny and other Sub-Doppler laser spectroscopy on relativistic beams and tests of Lorentz invariance. PHYSICAL REVIEW A 80, 022107, 2009
8. – А.Эйнштейн К электродинамике движущихся тел. Собрание научных трудов. Том 1. М.: Наука, 1965, 701 с.
9.- Е.А. Бутяев Загадки природы Гл. 4 О противоречивости различных интерпретаций красного смещения http://butjaev.narod.ru/BIB/gl4.pdf
10. - С.Ю. Юдин //Влияние скорости гравитации на смещения параметров орбит планет// Волгоград, 2013, 144 с. http://modsys.narod.ru