…………………. СКОРОСТЬ ГРАВИТАЦИИ
Часть 1 -.О РАВНОДЕНСТВИЯХ ГИППАРХА И ПТОЛЕМЕЯ
………………………….вторая редакция 09.04.2012 (исправленная)
С. Ю. Юдин …http://modsys.narod.ru.. . .modsys@narod.ru
Сегодня мы не найдем пожалуй не одной работы, посвященной Птолемею или Гиппарху, где бы ни говорилось о том, что Гиппарх определил моменты равноденствий правильно, а Птолемей не правильно и, по этому, прецессию (предварение равноденствий из за прецессии Земной оси при вращение Земли) Гиппарх определил очень точно (в пределах нескольких процентов), а Птолемей определил очень не точно (ошибка составляет 50%). Но при этом забывают упомянуть, что, используя каждый свои даты равноденствий и летнего солнцестояния, они определили продолжительности сезонов года (весны и лета), а по ним получили одни и те же значения эксцентриситета орбиты Земли и положение ее перигелия. При этом, и Гиппарх и Птолемей по современным представлениям определили не правильно значения эксцентриситета орбиты Земли (ошибка составляет 20%) и правильно значение долготы перигелия (используя при этом в расчетах неправильное значение эксцентриситета). Данную неувязку современных теорий с данными наблюдений древних астрономов можно бы было, как всегда, объяснить недостаточной грамотностью древних астрономов (в свете современных теорий) и не точностью их приборов, но здесь другой случай. Ведь все исламские астрономы (кроме АльХорезми) опять таки определили эксцентриситет орбиты Земли согласно современным теориям движения планет очень точно, а данные европейских астрономов (даже в XVII веке) и АльХорезми (IX век) совпали с данными Гиппарха и Птолемея.
Но, прежде чем перейти к загадке правильного, с точки зрения современных теорий движения планет, определения моментов равноденствия исламскими учеными, жившими в Азии в X … XIV веках, и неправильного с точки зрения современных теорий, живших в Европе (Испания), а также всех других европейских ученых до XVII века включительно, т.е. включая и Коперника и Кеплера, хотелось бы пояснить, откуда у меня возникла эта проблема. Дело в том, что сейчас я пытаюсь по экспериментальным данным наблюдений за планетами и Солнцем определить скорость распространения гравитации. Влияние этой скорости отражается на изменении параметров эллиптических орбит планет и со временем такие параметры, как наклон плоскости орбиты к эклиптике, эксцентриситет эллипса орбиты и другие немного изменяются. Эти изменения очень маленькие и трудно поддаются измерению, по этому их вычисляют за период в 100 лет и называют вековыми изменениями. В таком случае, естественно, было бы сравнить современные значения параметров орбит с теми параметрами, какие были тысячу или даже две тысячи лет тому назад, т.к. за такой промежуток времени эти изменения должны стать заметными.
Можно было бы и не вычислять самому эти вековые изменения параметров орбит, а просто воспользовался данными, которые уже получены современными астрономами и заложены в их теории, но их теории, как будет показано ниже, противоречат большинству данных древних астрономов, по этому я и решил сам определить вековые изменения параметров орбит. А получается такое противоречие по тому, что в современных теориях параметры орбит планет получены обработкой только современных данных наблюдений. Более того, они получены не прямой обработкой данных наблюдений, а из математических моделей, построенных с использованием различных физических теорий и, следовательно, в первую очередь отражают физические теории, а потом уже данные наблюдений (подробный анализ смотрите ниже). А начал я определять параметры орбит по таблицам древних астрономов, т.е. астрономов доньютоновской эпохи, чтобы хотя бы в общих чертах увидеть изменения параметров орбит на большом промежутке времени.
Естественно, в этих таблицах, кроме таблиц XVII века, при расчете эфемерид, т.е. положений планет на заданный момент времени в системе координат текущей эпохи, используется геоцентрическая подвижная система координат и планеты движутся не по эллипсам, а по различным эксцентрам, но положения планет в полярной системе координат по двум углам рассчитываются в этих таблицах довольно таки точно. Я, например, рассчитал по ним даже несколько солнечных и лунных затмений, которые были в наше время, и результаты почти по всем таблицам были удовлетворительные. А для определения по этим таблицам эллиптических параметров орбит планет в гелиоцентрической системе координат я в программе Solsys6 сделал дополнительную форму (подпрограмму), на которой для определения этих параметров использую методы многофакторного планирования. А, т.к. параметры орбит всех планет зависят от параметров орбиты Земли, с которой эти планеты и наблюдаются, то я начал с определения параметров орбиты Земли для моментов времени, в которых были созданы эти таблицы. Если кого-то интересует методика извлечения параметров орбит планет из таблиц, то скачать программу Solsys6 можно с зеркала моей домашней страницы здесь http://modsys.narod.ru из раздела Программы.
В результате у меня получилось, что угол наклона орбиты Земли к плоскости эклиптики и угол восходящего узла, полученные по этим таблицам и преобразованные к стандартной эпохе J2000, точно совпали с данными современных теорий. Вообще-то, если созданная мною методика определения параметров орбит верна, то такой результат мы и должны были получить, т.к. в таблицах получаются геоцентрические эклиптические координаты планет и Солнца для текущей эпохи и Земля в них априори движется в плоскости эклиптики. Следовательно, используя современные формулы преобразования координат к стандартной эпохе J2000, мы и должны были получить современные значения этих параметров. Полученные мною значения положения перигелия орбиты Земли не очень сильно отличаются от современных данных, а вот значения эксцентриситета орбиты Земли получились сильно отличающимися от заложенных в современные теории (кроме данных Аль Баттани). Я пытался найти и размер большой полуоси эллипса, но не удачно, т.к. для Земли по данным наблюдений за Солнцем это сделать, наверное, не возможно (полученные мною данные будут даны ниже). А вот данные по угловой скорости движения планет у меня получились очень противоречивые (объяснение этому смотрите ниже, при рассмотрение методик создания теорий движения планет).
Здесь уже можно было бы сделать вывод, о том, что параметры орбит планет заложенные в современные теории не соответствуют действительности для времени до 1800 года, но
параметры орбиты Земли, полученные мною по таблицам Аль Баттани, практически совпали с параметрами современных теорий. По этому, надо было провести дополнительное исследование и выяснить, кто же был не прав – Аль Баттани, или все остальные астрономы доньютоновской эпохи, таблицы которых я использовал. Для этого я решил ознакомиться с методикой, по которой астрономы экспериментально определяли эксцентриситет эксцентра и положение афелия Солнца, а потом по их экспериментальным данным самому рассчитать эти параметры и уточнить их с учетом систематических погрешностей, которые были в их измерениях и в их методике. Давайте посмотрим, что из этого получилось, а если кто-то не очень силен в астрономии, то, прежде чем перейти к этому вопросу, полезно будет прочитать следующие два абзаца.
Моменты равноденствий человечество стало определять, наверное, за несколько тысяч лет до нашей эры. Это нужно было для того, чтобы определить продолжительность тропического года и знать моменты начала времен года, для проведения сельскохозяйственных работ. Но нас больше интересует то, что по этим моментам, мы можем определить положение в пространстве воображаемой линии пересечения плоскости эклиптики, по которой движется Земля, и плоскости экватора Земли. Это необходимо для того, чтобы определить положение осей в экваториальной декартовой системе координат, в которой мы можем фиксировать положения небесных объектов в любой момент времени. Ось X в момент весеннего равноденствия (ВР), если мы находимся в северном полушарии на освещенной Солнцем стороне Земли, будет направлена в сторону Солнца, ось Z перпендикулярно экватору в направление северного полюса, а ось Y перпендикулярно плоскости XZ на восток. В момент осеннего равноденствия (ОР) ось Z сохранит свое направление, а направление осей X и Y будет определяться, наоборот, в направление от Солнца и на запад. Кроме того, в точках ВР и ОР геометрическое Солнце будет всходить почти точно на востоке, а заходить почти точно на Западе и, вследствие этого продолжительность дня и ночи будет приблизительно одинаковой. Но моменты равноденствия никто не определяет по продолжительности дня и ночи т.к. сам термин «равноденствие» носит чисто условный характер, а величина промежутков дня и ночи будет обусловлена и многими другими факторами (рефракция, высота над уровнем моря, движение Земли за сутки по эклиптике).
Надо также сказать, что древние астрономы не знали декартовой системы координат и пользовались полярными горизонтальной, экваториальной и эклиптической системами координат, в которых положение небесных объектов они фиксировали с помощью двух углов. Угол между осью X и направлением на объект в плоскости XY в экваториальной системе координат это прямое восхождение (в эклиптической долгота), а угол между плоскостью XY и направлением на объект это склонение (в эклиптической широта). В горизонтальной системе координат положение в плоскости горизонта от направления на Юг в сторону Запада это азимут, а угол между плоскостью горизонта и направлением на объект это высота.
И хотя такая система координат с фиксацией положения осей в эпохе даты, является относительной, т.к. положение оси X относительно неподвижных звезд со временем немного меняется, но ее создание было большим достижением древних астрономов и позволяет нам и сейчас использовать их данные наблюдений, зная на какой угол повернулась ось X. Этот угол называется прецессией, т.е. предварением равноденствий, и из-за прецессии равноденствия наступают каждый год немного раньше. Первым среди известных нам астрономов на это обратил внимание Гиппарх (140 лет до н.э.), но это явление в древнем Вавилоне было известно и задолго до него. Гиппарх даже вычислил почти точное значение прецессии, т.к. за то время, когда у греков закрепились обозначения в экваториальной системе координат (примерно 400 лет до н.э.) точка ВР сместилась от своего первоначального положения (направление на первую звезду в созвездие Овна – находиться на кончике рога барана) на несколько градусов, т.к. за 100 лет прецессия составляет 1,4 градуса. Сейчас точка ВР находится уже в созвездие Рыб, но во избежание путаницы в полярной системе координат направление оси X продолжает обозначаться знаком Овна (^j^).
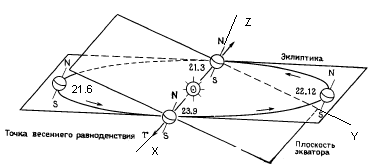
Рис.1. Положения Земли в моменты равноденствий и солнцестояний. Воспроизведено (с изменениями) из работы [12].
А теперь давайте рассмотрим как же древние астрономы (примерно с V века до н.э., т.е. с момента, когда у нас есть их данные наблюдений) определяли моменты равноденствий и солнцестояний. Простейшим астрономическим прибором является гномон, т.е. колышек установленный строго вертикально. По длине его тени астрономы определяли моменты зимнего и летнего солнцестояний. Если точка наблюдения находится на широте больше чем угол наклона экватора к эклиптике, то в момент солнцестояния, отбрасываемая им тень будет самой короткой в момент летнего солнцестояния и самой длинной в момент зимнего солнцестояния. Более сложным прибором был меридианный круг, который состоял из двух колец расположенных в одной плоскости и вращающихся относительно друг друга. Устанавливался он по отвесу вертикально и строго в плоскости меридиана, т.е. так, чтобы был направлен на Солнце, когда гномон отбрасывал самую короткую тень за день, т.е. в 12 часов. На одном круге имелись деления от 0 до 360 градусов, а на другом были на противоположных сторонах закреплены две призмы, которые указывали градусы, на которые внутренний круг был повернут относительно наружного (неподвижного) в тот момент, когда тень от одной призмы падала на другую. Птолемей описывает также квадрант, который является как бы четвертью меридианного круга, и устанавливается также по отвесу и в плоскости меридиана, но здесь имеется четверть только неподвижного круга с градусами от 0 до 90. А высота Солнца определяется по тому на какое деление падает тень от цилиндрика закрепленного точно в середине круга, от которого отрезали эту четверть.
Но самым интересным для нас инструментом (почему станет ясно дальше) является экваториальное кольцо, которое устанавливалось строго в плоскости экватора Земли.
Принцип действия экваториального кольца такой, что зимой освещается нижняя (южная) сторона кольца, а летом верхняя (северная) а в моменты равноденствий освещаются обе стороны кольца. Вообще-то, если бы Солнце было точечным источником света, то такого бы не наблюдалось (из-за толщины кольца), но вследствие дифракции и того, что видимый диаметр Солнца составляет 0,54 градуса, мы можем наблюдать такой момент. У исламских астрономов тоже были приборы подобные квадранту, но, обычно они имели очень большие размеры и были стационарными, что увеличивало точность наблюдений, а для наблюдений в произвольном месте они использовали различные астролябии. Описывать устройство астролябии не имеет смысла, т.к. к решению нашей задачи это не имеет отношения, а вот то, как они определяли моменты равноденствий стоит описать. Делалось это по траектории солнечного зайчика, который попадал в помещение через отверстие в крыше и перемещался внутри помещения по сферической поверхности, где предварительно было определено место экватора.
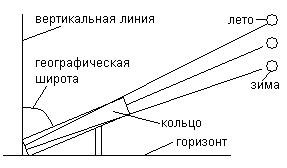
Рис.2. Схема установки экваториального кольца и траектории движения лучей Солнца летом, зимой и в моменты равноденствий.
Естественно, если момент равноденствия наступал не днем, а ночью, то наблюдать момент равноденствия непосредственно не возможно ни на экваториальном кольце, ни с помощью солнечного зайчика. В таком случае замеряли на сколько угловых минут отклонялся луч Солнца в день после этой ночи и в день перед этой ночью, а потом, интерполируя эти отклонения, находили время, когда было равноденствие. А для измерения продолжительных отрезков времени тогда использовались водяные и солнечные часы или горящие свечи, а также величина прямого восхождения того или иного небесного объекта, т.к. было известно в какое время этот объект проходит через местный меридиан. Например, Солнце в 12 часов дня, а середины знаков зодиака через каждые 2 часа.
А теперь давайте, наконец-то, перейдем непосредственно к экспериментальным данным. В таблице 1 я привожу параметры орбиты Земли, которые я получил, обрабатывая данные эфемерид полученных по таблицам древних астрономов [5] и современных теорий. Таблицы тоже являются теориями движения планет, но фенологическими, по которым производится расчет двух углов в полярной системе координат, определяющих положение планеты в пространстве относительно Земли. Здесь и далее я использую обозначение для эксцентриситета эллипса Eks, а для эксцентриситета эксцентра Eks2. При использование теории движения по эллипсу и по эксцентру примерно одинаковые результаты видимого движения планет получаются, когда Eks2=2* Eks и чем меньше значение Eks, тем меньше эти различия. По этому, т.к. значения Eks для планет Солнечной системы очень маленькие, мы можем полностью доверять значениям параметров эллиптических орбит планет полученных обработкой данных таблиц эфемерид древних астрономов.
Вот только у древних астрономов не всегда правильно были учтены вековые изменения параметров орбит, по этому полученные по их теориям данные будут больше соответствовать тому году, когда эти таблицы были созданы и для долготы города, где они были созданы. Коротко поясню, почему это будет так. Координаты всех планет в таблицах определяются исходя из направления на точку весеннего равноденствия а также (в геоцентрических таблицах) от положения апогея Солнца. А, т.к. оба эти значения со временем изменяются, то, чем дальше от даты, для которой определены эти параметры, тем будет больше погрешность, т.к. не только сами величины апогея и направления на точку весеннего равноденствия для конкретных дат определены авторами таблиц с погрешностью, но и изменение со временем этих величин также определены с какой то погрешностью. А т.к. во всех таблицах время дается местное, то необходимо знать долготу города, для которого они составлены. По этому я по имеющимся у меня данным попытался определить время и город создания перечисленных ниже таблиц, которые были в моем распоряжении.
Almagest – 132-147 год, Клавдий
Птолемей (87-165?), около Александрии (Египет).
В своей работе Птолемей использовал работы не только греческих ученых Аратуса,
Евдокса, Архимеда, Калиппа и особенно Гиппарха с его эпициклами и обширными
данными наблюдений, но и работы египетских и вавилонских астрономов. Как,
указывается в литературных источниках, быстрее всего Птолемей значение апогея
Солнца не определял сам и просто взял его по данным Гиппарха, т.к. считал, что
апогей не смещается, а отсюда получается, что использовать эти таблицы надо не для
147 г. н.э., а для 150 г. до н.э., когда жил Гиппарх. Кроме того, многие
астрономы, после Лапласа, пишут о том, что Птолемей определил
теоретическую долготу Солнца с ошибкой в 1 градус. Момент осеннего
равноденствия, установленный Птолемеем в 14 час 25 сентября 132 г. точно соответствует принятой Птолемеем (ошибочной) продолжительности тропического года (если
отсчитывать от момента осеннего равноденствия, найденного Гиппархом в 146 г. до н.э.). По этому, я рассчитаю по таблицам Птолемея параметры орбит планет и для 147 г н.э. и для 150 г. до н.э.
Handy – 500-700?, индийские астрономы?, г. Арина? – сейчас г. Уджайн (Индия).
Это более поздняя версия таблиц Птолемея сделанных (судя по названию) в Индии,
куда Альмагест попал в 4-5 веке вместе с учеными, которые покинули Александрию
после разрушения ее научного центра в 391 г. И быстрее всего, это просто перевод таблиц Птолемея, а полученные по ним данные для 0, 300 и 500 годов
подтверждают этот вывод, т.к., полученные по ним данные, полностью совпадают с
данными Almagest. По этому, в дальнейшем использовать эти таблицы я не буду.
AlKhwarizmi – 824 год, Мухаммад Ибн Мусса Аль Хорезми (780-850?), Багдад?
(Ирак) или Кордова? (Испания). Аль Хорезми в своей работе использовал не только
Альмагест, но и труды индийских астрономов, т.к. сам переводил на арабский язык
некоторые их работы, по этому применял и десятеричную систему счисления
индийцев, где ввел цифру ноль, и их синусы и тангенсы, вместо шестидесятеричной
системы Птолемея с его таблицей хорд. Хотя Аль Хорезми работал в Багдаде, но он
использовал много трудов индийских астрономов, по этому за нулевой меридиан им
приняты координаты города Арина – сейчас г. Уджайн в штате Мадхья-Прадеш
(Индия) и, следовательно, время в его таблицах соответствует этому меридиану,
хотя позже Аль Хорезми за нулевой меридиан стал принимать, как и Птолемей,
Канарские острова. А, что касается даты создания таблиц, то, 824 год это год
написания его трактата о календарях, но это единственная дата, которая
проставлена однозначно в его работах. Вот только, эти таблицы не являются
оригинальной версией его таблиц, т.к. оригинальная версия не сохранилась. Более
того, известно, что у него в Зидже афелий Солнца был 77,92 градуса (возможно,
что это данные индийских астрономов), а по таблицам для 800 года получается
81,07, что очень подозрительно. Ведь до того, как Аль Бируни занялся вопросом о
смещение афелия Солнца, считалось, как он пишет, что он не смещается. И Аль
Бируни в своем исследование приводит данные различных авторов (около десяти) от
81 до 84 градусов для 833-1017 годов, но не упоминает при этом Аль Хорезми и
его 77,92 градуса. Таким образом, в используемых мною таблицах долгота афелия
получается вроде как уже с прецессией от 622 года, что как-то не очень обычно
(хотя сам термин //обычно// не очень применим для таблиц Аль Хорезми, т.к. это
только вторые самостоятельные таблицы после таблиц Птолемея). А, кроме того, в
этих таблицах используется для прецессии теория Сабита ибн Курры (826-901), но
таблицы Аль Хорезми должны были быть созданы до того, как Курра, судя по дате
рождения, смог бы вырасти, чтобы создать свою теорию, что еще больше запутывает
этот вопрос. Могу еще добавить, что на латынь астрономические таблицы, основы
тригонометрии и Алгебру Аль Хорезми перевели только в 12 веке, а сами таблицы в
1007 году переработал для Европы Маджрити, который, как пишут, только привел их
к полудню меридиана Кордовы. В общем, задача датировки этих таблиц и
определения места, для которого они должны применяться, очень сложная, но
надеюсь, что авторы различных версий таблиц Аль Хорезми не сильно подкорректировали
его данные по параметрам орбит и это остались именно таблицы Аль Хорезми, а,
судя по полученным мною данным, возможно использование этих таблиц и для 1000 года.
Кстати в кхмерских таблицах SEAC (Combodian) http://www.thep.lu.se/~larsg/SEAC.zip апогей
Солнца принят также, как и в таблицах Аль Хорезми 80 градусов и эксцентриситет
эксцентра 0,03888, что соответствует эксцентриситету эллипса 0,01944. Наверное,
эти таблицы составлены по данным таблиц Аль Хорезми и попали в Юго-Восточную
Азию из Китая, где использовались таблицы Аль Хорезми.
AlBattany – 910 год, Мухаммад Аль Баттани (858-929), Ракка – сейчас Халеб
(Сирия).
Эти таблицы полностью базируются на таблицах Птолемея, но Аль Баттани существенно
уточнил параметры кинематической модели Птолемея, по этому, его таблицы, как и
таблицы Аль Хорезми, отличались более высокой точностью, чем таблицы Птолемея.
При этом он не только разработал таблицу котангенсов, но и начал применять
тригонометрию на сфере, по этому его считают одним из основателей
тригонометрии. А, после перевода его работ на латинский язык, а позже на
испанский, он стал самым известным в Европе исламским ученым. Как известно, его
таблицы существовали в двух вариантах и, быстрее всего, у нас более поздняя
версия, но, как пишут, эти варианты мало чем отличаются. А, как пишет Наллино,
на сегодняшний день сохранился только один экземпляр таблиц на арабском языке и
быстрее всего он был написан в 1100 году. Но, как показывают полученные мною
данные, параметры орбит в этих таблицах все же больше соответствуют 900 году,
т.е. примерному году создания оригинальной версии.
Toledan – 1080 год, Ибрагим Аз Заркали (1029-1087), Толедо (Испания).
Это европейская копия таблиц Аль Баттани, которые, как и многие другие научные
работы попали в Европу через арабскую Испанию, которая тогда входила в
Кордовский халифат, т.е. была частью исламской империи (численность населения в
столице халифата Кордове была около 500 тыс. человек, в Багдаде 1500 тыс. чел,
а в Париже 100 тыс. чел.). И, хотя в 1085 г. Толедо был завоеван королями Кастилии, он еще долго оставался центром научной мысли в Европе. Но первыми
европейскими таблицами были, все-таки, таблицы Аль Хорезми (с учетом и
выдержками из таблиц Аль Баттани), пересчитанными Маслама ибн Ахмадом для
меридиана Кордовы. При этом, в Толедских таблицах, просматривается и влияние
других арабских таблиц, например, по вычислению прецессии, т.к. Аль Баттани
отрицал для прецессии теорию Сабита ибн Курры, которая использована в Толедских
таблицах. Я думаю, что, наверное, к 1080 г. эти таблицы и можно отнести, но, судя по полученным мною по этим таблицам параметрам орбиты Земли для 800 и 1080
годов, изменения, внесенные в оригинальные таблицы Аль Баттани не пошли на пользу
этим таблицам и результаты по этим таблицам для любого года получаются хуже,
чем по таблицам Аль Баттани, хотя и близки к ним. В дальнейшем использовать эти
таблицы я не буду.
Alfonso – 1252 год, под руководством короля Кастилии Альфонса Х, Толедо (Испания).
Таблицы составлены коллективом авторов, во главе которых стоял Исаак бен
Сайд. Эти Альфонсийские (Альфонсовы) таблицы были первыми чисто европейскими
таблицами, хотя основывались на таблицах Птолемея и Толедских таблицах
аз-Заркали, и были приведены к первому году правления Альфонсо X. Как
известно, оригинальная версия этих таблиц сохранилась в Париже только частично
и, по этому, это какая-то более поздняя их копия, которая возможно и приведена
к более позднему времени, но я буду их использовать для 1252 года.
Prutenic – 1551 год, Э. Рейнгольд (1511-1553), Нюрнберг.
Это первые гелиоцентрические таблицы после публикации в 1543 году Коперником
своей теории, но выполненные также как и таблицы Птолемея, с дифферентами и
эпициклами и отпечатаны в 1551 г. в Тубингене. Наверное, их можно применить к
1540 году, но из-за множества ошибок эти таблицы дают очень не стабильные
результаты, по этому использовать их я не буду (вернее технически не могу).
Ticho – 1600 год, Тихо Браге (1546-1601), Ураниенборг (Дания).
Rudolphino – 1627 год, Кеплер (1571-1630), Ураниенборг (Дания).
Т. Браге составил свои таблицы, после того как перебрался в 1599 году из своей,
оставшейся без финансирования, обсерватории Ураниенборг на острове Вэн около
Копенгагена к королю Рудольфу 2 в столицу Римской империи – Прагу. Но он их
успел закончить только для Солнца и Луны, по этому я эти таблицы в полном
объеме использовать не могу. Затем эти таблицы, после открытия своих законов,
доделывал его ученик Кеплер. Т.к. его таблицы базируются на астрономических
наблюдениях Т. Браге, то разумнее их применять для 1600 г.
Streete – 1661 год, Стрит (1622-1689), Лондон
Wing – 1668 год, Винг (1619-1668?), Лондон
Т.к. таблицы и Стрита и Винга составлены примерно в одно и тоже время и при
этом они использовали примерно одни и те же данные наблюдений, для определения
параметров орбит планет в своих таблицах, то чисто по техническим причинам,
чтобы точки не сливались на графике, разнесем их немного по времени. Для таблиц
Стрита примем 1620 год, а для таблиц Винга 1640 год. Не смотря даже на то, что,
например, сами таблицы Стрита были опубликованы только в 1664 как отдельное
приложение к его книге по астрономии, а второй (исправленный) выпуск книги с
таблицами появился уже в 1710. Кстати, очень интересный факт - Стрит не имел
никакого университетского образования и не был членом ни одного из научных
обществ, но при этом имел связи с астрономами в Англии и за границей.
New0,
New1,
New2
– 1896 год, Ньюком (1835-1909), Вашингтон
Эта аналитическая теория, т.е. теория с использованием законов Ньютона для аппроксимации данных наблюдений, заменила аналитическую теорию французского астронома Леверье. Теория New2 (впрочем как и теория Леверье) с небольшими уточнениями используется и сейчас наравне с различными численными теориями, но я в своей работе пользуюсь теорией New0, т.к. меня интересуют только постоянные воздействия от других планет, приводящие к смещению параметров орбит планет, хотя в 6-ой версии программы Solsys у меня была и New1. Индексы 0, 1 и 2 здесь означают 0- учитываются только постоянные воздействия от других планет, 1- учитываются как постоянные, так и 1-е периодические возмущения от других планет, 2- учитываются как постоянные, так и 1-е и 2-е периодические возмущения от других планет.
JPL2 – 1997 год, Лаборатория Реактивного Движения (подразделение НАСА), Вашингтон.
Это численная теория, т.е. полученная решением системы дифференциальных уравнений, описывающих движение планет, численными методами на компьютере и оформленная в виде эфемерид DE405, данные для которых рассчитываются по аппроксимациям данных полученных в численной теории. В настоящее время известны так же такие эфемериды как ЕРМ2004 (Россия) и INPOP06 (Франция), но все подробности того, как они получены не раскрываются и, например, в JPL это является коммерческой тайной, известной лишь нескольким сотрудникам. Но, не смотря на это, эфемериды DE405 в настоящее время являются де-факто эталоном не только для всех теорий, но даже все данные наблюдений бракуют, если они расходятся с этими эфемеридами.
JPL0 - Эта теория похожа по описанию на аналитические теории, но получена она аппроксимацией не экспериментальных данных наблюдений, а расчетных данных численной теории, т.е. эфемерид DE405, но без учета периодических воздействий от планет и по этому имеет индекс 0.
Как видим, с таблицами от Птолемея до Альфонсовых включительно есть некоторая
неопределенность, как по авторству этих таблиц или, скажем так, степени
редактирования их в более позднее время другими астрономами, так и по некоторым
астрономическим постоянным, использованным в них, но будем надеяться, что
переписчики, переводчики и модернизаторы этих таблиц вносили в них не очень большие
изменения, и то время, для которого я рекомендую их использовать, даст хотя бы
ориентировочные значения параметров орбит планет для этого времени, которые я
привожу в таблице 1.
Таблица 1. Параметры орбиты Земли (в эпохе даты), полученные по данным эфемерид таблиц древних астрономов и современных теорий.
|
название таблиц, теорий |
год |
долгота перигелия AlfaP |
эксцентриситет орбиты Eks |
|
Almagest (Птолемей) |
140 |
65,29 |
0,02076
|
|
AlKhwarizmi (АльХорезми) |
800 |
83,29 |
0,01934
|
|
AlBattani (АльБаттани) |
900 |
82,56 |
0,01732
|
|
Alfonso (Альфонсовы) |
1252 |
88,62 |
0,01890
|
|
Rudolphine (Кеплер) |
1600 |
95,77 |
0,01800
|
|
Streete (Стрит) |
1620 |
96,18 |
0,01732
|
|
Wing (Винг) |
1640 |
96,44 |
0,01788
|
|
New0 (Ньюком) |
1900 |
101,2208 |
0,01675
|
|
JPL0 (НАСА) |
2000 |
102,9377 |
0,01671
|
Но, кроме таблиц древних астрономов, в нашем распоряжение имеются и некоторые экспериментальные данные наблюдений, по которым древние астрономы определяли параметры орбит планет для своих теорий. В таблице 2 приведены такие данные по продолжительности сезонов года, а в таблице 3 параметры, которые получаются из данных определения моментов равноденствий и летнего солнцестояния при использовании методики, которой пользовались древние астрономы. Здесь надо заметить, что в таблице 2 для первых наблюдений продолжительность года быстрее всего дана с округлением, т.к. и Гиппарх и Птолемей пишут о том, что продолжительность тропического года (от равноденствия до равноденствия) меньше 365,25 дней на 1/300 часть. Известно им было и то, что тропический год отличается от звездного, продолжительность которого определяется относительно неподвижной системы координат, а не относительно линии равноденствий, которая смещается со временем.
Таблица 2. Продолжительность сезонов года.
|
Автор, город и источник |
год |
весна |
лето |
осень+ зима |
итого |
|
Метон и Евктемон, Афины [3] |
-431 |
95 |
92 |
178 |
365 |
|
Калипп, Афины [4] |
-350 |
94 |
92 |
179 |
365 |
|
Вавилонские астрономы [4] |
-150 |
94,5 |
92,73 |
178,03 |
365,26 |
|
Гиппарх, Родос [1,3] |
-140 |
94,5 |
92,5 |
178,25 |
365,25 |
|
Птолемей, Александрия [1] |
140 |
94,542 |
92,458 |
178,25 |
365,25 |
|
Бану Муса, Багдад [2] |
833 |
93,683 |
93,017 |
178,542 |
365,242 |
|
Халид ал Мервази и др. Багдад [2] |
844 |
93,91 |
93,156 |
- |
- |
|
Аль Баттани, Рака [2] |
883 |
93,583 |
93,031 |
- |
- |
|
Сулейман ибн Исма, Балха [2] |
889 |
93,4585 |
93,0403 |
178,9586 |
365,4572 |
|
Абу Вафа, Багдад [2] |
975 |
93,502 |
93,119 |
- |
- |
|
Аль Бируни, Джурджания [2] |
1016 |
93,466 |
93,05 |
- |
- |
Таблица 3. Параметры орбиты Земли, рассчитанные по продолжительности сезонов года.
|
автор |
год |
дней |
весна |
лето |
AlfaP |
Eks2 |
Eks |
|
Евктемон |
-431 |
365 |
95 |
92 |
56,306 |
0,04654 |
0,02327 |
|
Калипп |
-350 |
365 |
94 |
92 |
60,253 |
0,03469 |
0,01735 |
|
Вавилон |
-150 |
365,26 |
94,5 |
92,73 |
68,95 |
0,04238 |
0,02119 |
|
Гиппарх |
-140 |
365,25 |
94,5 |
92,5 |
65,429 |
0,04137 |
0,02069 |
|
Птолемей |
140 |
365,25 |
94,5417 |
92,4583 |
64,532 |
0,04167 |
0,02084 |
|
Бану Муса 1 |
833 |
365,25 |
93,683 |
93,042 |
81,113 81,386* |
0,03569 0,03569* |
0,01785 0,01785 |
|
Бану Муса 2 |
833 |
365,242 |
93,683 |
93,017 |
80,725 |
0,03554 |
0,01777 |
|
Мервази |
844 |
365,25 |
93,91 |
93,156 |
80,362 80,370* |
0,03874 0,03880* |
0,01937 0,01940 |
|
Аль Баттани |
883 |
365,25 |
93,583 |
93,031 |
82,12 82,127* |
0,03463 0,03400* |
0,01732 0.01700 |
|
Сулейман 1 |
889 |
365,25 |
93,4585 |
93,0403 |
83,837 83,850* |
0,03351 0,03350* |
0,01676 0,01675 |
|
Сулейман 2 |
889 |
365,4572 |
93,4585 |
93,0403 |
83,669 |
0,03260 |
0,01630 |
|
Абу Вафа |
975 |
365,25 |
93,502 |
93,1194 |
84,530 84,596* |
0,03452 0,03450* |
0,01726 0,01725 |
|
Аль Бируни |
1017 |
365,25 |
93,466 |
93,05 |
83,896 85,218* |
0,03365 0,03429* |
0,01683 0,01715 |
|
Ньюком |
1900 |
365,2435 |
92,832 |
93,608 |
101,450 101,221** |
0,03351 0,03429** |
0,01675 0,01675 |
|
JPL (НАСА) |
2000 |
365,2435 |
92,759 |
93,65 |
103,241 102,938** |
0,03346 0,03342 ** |
0,01673 0,01671 |
* - параметры, рассчитанные самим Аль Бируни при тех же исходных данных
** - значения параметров, заложенные в аналитические теории планет Ньюкома и Лаборатории Реактивного Движения (JPL), а приведенные продолжительности сезонов и всего года рассчитаны мною по этим теориям.
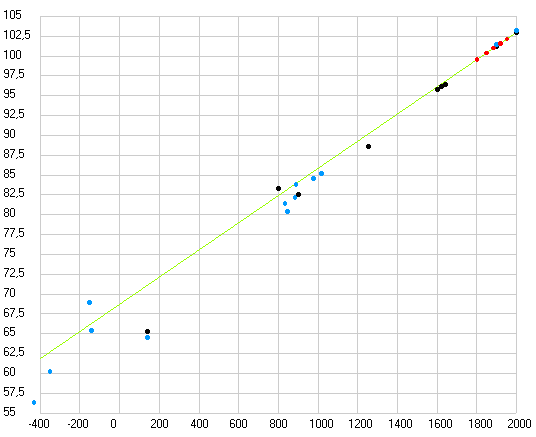
Рис. 3. Долгота перигелия орбиты Земли по данным таблиц древних астрономов и двум современным теориям (черные точки), рассчитанная по продолжительности сезонов года (голубые точки) и полученная при обработке данных различных обсерваторий с 1800 по 1983 годы (красные точки). Прямая линия отражает данные современных теорий.
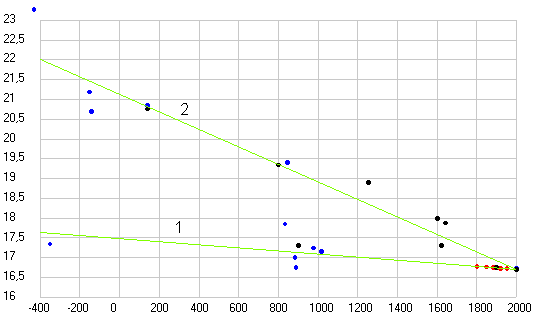
Рис. 4. Эксцентриситет орбиты Земли (увеличено в 1000 раз) по данным таблиц древних астрономов и двум современным теориям (черные точки), рассчитанный по продолжительности сезонов года (синие точки) и полученный при обработке данных различных обсерваторий с 1800 по 1983 годы (красные точки). Прямая 1 построена по современным теориям (объединяет нижнюю группу точек), а прямая 2 аппроксимирует верхнюю группу точек.
Как видим все точки, полученные как из таблиц, так и прямым расчетом по продолжительности сезонов года для значения долготы перигелия орбиты Земли (афелия Солнца) хорошо ложатся на прямую линию, но все они лежат немного ниже значений заложенных в современные теории движения планет. А вот точки эксцентриситета орбиты Земли (Солнца) не все ложатся на одну прямую. Те, что получены из таблиц (кроме таблиц Аль Баттани) ложатся на одну прямую (2) и она отстоит далеко от прямой, отражающей параметры, заложенные в современные теории. А, точки, полученные прямым расчетом, разделились. Все точки мусульманских астрономов, рассчитанные по данным Аль Бируни (кроме Халида Мервази) лежат вблизи современных теоретических данных (1), а все точки астрономов домусульманской эпохи (кроме Калиппа) и после них совпадают с данными, полученными из таблиц (2).
Таким образом, в согласовании двух групп вековых изменений эксцентриситета орбиты Земли остается теперь надеяться только на данные наблюдений нескольких последних столетий, которые возможно будут изменяться по какой-то прямой проходящей между полученными нами двумя зависимостями 1 и 2. В таком случае можно будет предположить, что отклонение данных наблюдений древних астрономов от данных современных наблюдений вызвано ошибками в измерениях древних астрономов, как в одну, так и в другую сторону. Данные последних столетий, конечно же, охватывают очень маленький период наблюдения для заметных изменений параметров орбит, но будем надеяться, что высокая точность этих наблюдений позволит нам получить более-менее достоверные результаты.
Вот только путь к началу обработки этих данных у меня оказался длиною в год, т.к. вначале я не мог найти данных по Солнцу, а сейчас выяснилось, что эти данные надо еще и дорабатывать. А обнаружилось это так. На сайте Парижского бюро долгот http://www.imcce.fr/host/podb/index.html и на сайте НАСА http://iau-comm4.jpl.nasa.gov/plan-eph-data/index.html я нашел данные наблюдений за всем планетам, но данных по Солнцу там не было. И первыми данными по Солнцу, которые я нашел, были данные Николаевской обсерватории http://www.mao.nikolaev.ua/ccd_1/cat_r.php , но они были оформлены в виде таблиц HTML, а затем я нашел печатный отчет Парижской обсерватории за 1861 год http://www.archive.org/details/annalesdelobser02verrgoog . И вот тут у меня возникла потребность в написание программы, которая бы читала данные наблюдений, оформленные в виде таблиц Excel и записанные там в любом формате, а потом записывала бы их в файл в формате, который используется в Парижском бюро долгот (я его называю формат BDL).
Связано это с тем, что моя программа Solsys, на которой я обрабатывал все данные наблюдений за планетами, была приспособлена для работы только с файлами в формате BDL. И первоначально я и сделал программу ObsData для чтения данных из таблиц Excel, где они могут быть записаны в произвольном формате, и для последующей их записи в файл в формате BDL. Но потом я нашел данные по Солнцу и на сайте НАСА, где они были записаны в файлах в формате Лаборатории реактивного движения (JPL) и добавил возможность преобразовать данные и из этого формата в формат BDL. А сейчас мне прислали и данные уже в формате BDL http://a-dovgiallo.narod.ru/SUN_1800_1969.rar и вроде бы острая потребность в этой программе отпала, по этому случись это раньше, то этой программы могло и не быть. Ее могло не быть, по крайней мере в этом виде, и если бы я раньше нашел данные в формате JPL, т.к. на самом деле они у меня давно были, но я из-за путаницы JPL с нумерацией Луны и Солнца в этих файлах и в эфемеридах DE405 не смог их своевременно идентифицировать как данные по Солнцу. Да и данные в формате BDL, которые мне прислали, оказывается, тоже имеются на сайте Парижского бюро долгот, но выложены они на FTP сервере без лишней рекламы и по этому узнать о том, что они там есть, можно только тупо просмотрев все папки самому.
Только вот работать с данными, даже уже выложенными на сайте Парижского бюро долгот в формате BDL, не очень удобно и я решил создать 2-ю форму программы для их доработки. Например, данные у них выложены в обратной последовательности, т.е. начиная с самых последних наблюдений, а работать с ними гораздо удобнее в прямой последовательности. Или, например, у них имеется явная ошибка в указание вида времени наблюдения, т.к. кругом указано ET, а как я выяснил должно быть указано UT, что при учете эфемеридной поправки приведет к искажению полученных результатов. А вот анализ одних и тех же данных, но из разных источников, например, обсерватории USNO на сайтах JPL и Парижского бюро долгот или Леверье в его отчете и на сайте Парижского бюро долгот окончательно убедили меня в необходимости создания второй формы программы.
Выяснилось, что в одних и тех же данных, опубликованных в разных местах, имеются нестыковки, которые без этой программы даже обнаружить было практически не возможно. Например, сравнивая данные наблюдений за Меркурием обсерватории USNO на 6’’ телескопе с 1913 по 1969 годы, но выложенные на сайтах JPL (в моей нумерации файл USNO1_G_60) и Парижского бюро долгот (файл USNO1_G_40) я обнаружил странные расхождения. Например, для наблюдений до 1949 года идут различные отклонения во времени наблюдения, но почти все менее 1 сек, а с 1949 года наблюдается или точно нулевое отклонение или точно 0,864 сек. Хотя есть и исключения, например, время наблюдений 26.9.1951 и 16.1.1952 года оба отличаются на 2,592 сек. И это при том, что расхождения почти кругом по долготе или нулевые или 0,015 или 0,030 или 0,045 угловых секунд, а по широте или нулевые или 0,01 угл.сек. Хотя и с координатами не все так гладко, по тому, что после 1955 года по широте расхождения становятся в интервале до 0,5 угл. сек, а по долготе с 1913 по 1918 год имеются расхождение почти кругом точно 1,2 угл. сек, а, например, для 9.11.1937 получается даже 209,7 угл. сек. Не говоря уже о том, что, например, в файле JPL есть данные по широте от 24.10.1929 и по долготе от 23.3. 1931, а в файле Парижского бюро долгот эти данные отсутствуют.
А, сравнивая данные наблюдений за Солнцем обсерватории USNO на 6’’ телескопе выложенные на сайте JPL (файл USNO0_G_60) и Парижского бюро долгот (файл USNO0_G_46), я обнаружил, не только аналогичные систематические расхождения в данных, например, частенько по долготе точно 1,2 угл. сек или по широте точно на 0,01 угл. сек, но и не единичные, а многочисленные пропуски в данных или по времени наблюдения, или по долготе или по широте в данных на сайте Парижского бюро долгот. Как то не очень верится, что все эти нестыковки всего-навсего небрежность таких аккуратных людей как астрономы, да еще при наличие у них компьютеров. Хотя, именно ошибками в работе компьютерной программы (аналогичной ObsData) и можно объяснить очень некачественный перевод данных наблюдения из одного формата в другой. И, быстрее всего, основная масса данных именно на сайте Парижского бюро долгот является копией данных с сайта JPL, но в другом формате, а такой вывод можно сделать по тому, что в одних и тех же данных пропуски по некоторым координатам имеются только на сайте Парижского бюро долгот.
Вообще то, теоретически можно предположить, что это не французская программа дает систематические погрешности и ошибки при конвертации данных наблюдений, а моя программа ObsData, т.к. в ней дата и время наблюдения сначала (после чтения данных из файла) всегда переводятся в юлианскую дату, а при записи переводятся обратно в формат BDL. Точно также и долгота и широта сначала переводятся в градусы, а потом в формат BDL. Но доказательством того, что именно программа французов работает не корректно, а не моя, является то, что при переводе с помощью программы ObsData, геоцентрических координат Меркурия обсерватории USNO на 6’’ телескопе сначала в топоцентрические, а потом опять в геоцентрические никаких расхождений этих данных с исходными не обнаружено (если не считать округления в последней значащей цифре угловых секунд). Точно также и при переводе данных по UT в данные по LT и потом назад опять таки нет никаких расхождений в датах и времени в формате BDL этих данных с исходными. Вот только радости от того, что правильно работает именно моя программа у меня мало, т.к. получается, что почти все опубликованные данные наблюдений имеют одного хозяина, а именно JPL, о порядочности сотрудников которой у меня сложилось не очень хорошее мнение.
Вот так и была создана программа ObsData, предназначенная для чтения данных наблюдения за планетами и Солнцем, которые записаны в произвольном формате, и для последующей автоматической записи их в одном из стандартных форматов, а конкретно в формате, который используется в Парижском бюро долгот (я его называю формат BDL). А можно и современные данные, уже записанные в файл в формате BDL, преобразовать из одной системы координат в другую, например, заданные в стандартной эпохе B1950 в эпоху даты или стандартную эпоху J2000, или топоцентрические экваториальные координаты преобразовать в геоцентрические. Или можно упорядочить данные по дате наблюдения, разбить их на несколько файлов или объединить в одном файле из двух, например, с разными датами наблюдений или с данными отдельно по широте и по долготе. Можно и сравнить между собою данные из нескольких файлов или данные из файла с данными, рассчитанными по аналитической теории JPL0 или численной (эфемериды DE405), а результаты сравнения можно посмотреть или в численном виде или на графике и при этом результаты в численном виде можно также записать в файл вместе со статистикой. А, т.к. в программе уже был режим сравнения данных наблюдения с расчетными данными, то я добавил еще и кнопку для расчета координат планет на произвольную дату по эфемеридам DE405.
Ну, а, для тех, кого сами данные наблюдений мало интересуют, эта программа может быть полезна в плане программирования, т.к. в тех случаях, когда код может быть полезен в плане обучения программированию я всегда вместе с исполняемыми файлами выкладываю и исходный код. В данном случае я его выкладываю на языке программирования Visual Basic 6.0. В коде Вы найдете не только примеры работы с файлами последовательного доступа или с таблицами Excel, но и код типовых функций перевода экваториальных координат в эклиптические и обратно, горизонтальных в экваториальные и обратно, из одной эпохи в другую, расчета поправок по рефракции, нутации, параллаксу, звездной и планетной аберрации, перевода календарных дат в юлианские и обратно и многое другое. А кого-то может быть заинтересует алгоритм сортировки данных или простейшая аналитическая теория JPL0, по которой можно рассчитывать координаты планет на любую дату. В общем, смотрите сами. А более подробно, как с возможностями программы, так и с порядком работы Вы можете ознакомиться непосредственно при работе программы, нажав кнопку About. Скачать программу ObsData можно с зеркала моей домашней страницы здесь http://modsys.narod.ru из раздела Программы.
А после того, как я наконец то нашел данные наблюдений различных обсерваторий за Солнцем с 1800 по 1983 год и написал программу ObsData, я, используя эту программу, преобразовал данные наблюдений к формату BDL и привел их все к всемирному времени UT и упорядочил по датам наблюдения. Затем я, с использованием программы Solsys, отбраковал эти данные по критерию разности расстояния между расчетным значением положения Земли (использовалась теория JPL0) и положением, получающимся из данных наблюдений. А затем с использованием программы ObsData объединил отбракованные данные в один файл и обработал эти суммарные данные наблюдений за Солнцем на программе Solsys. В результате я получил значения параметров орбиты Земли, которые привожу в таблице 4.
Таблица 4. Параметры орбиты Земли (в эпохе даты) по данным наблюдений различных обсерваторий с 1800 по 1983 год.
|
Годы наблюдений |
К-во наблюдений |
долгота перигелия AlfaP |
эксцентриситет орбиты Eks |
|
1800-1847 |
6763 |
99,6077 |
0,016781 |
|
1848-1883 |
8910 |
100,3664 |
0,016767 |
|
1884-1919 |
9243 |
100,9976 |
0,016750 |
|
1920-1951 |
13045 |
101,6123 |
0,016733 |
|
1952-1983 |
5441 |
102,1491 |
0,016722 |
Как мы видим, данные наблюдений последних столетий (на рис. 3 и 4 красные точки) подтверждают справедливость современных теорий и данные наблюдений мусульманских астрономов 9-12 веков по эксцентриситету орбиты (остальные параметры хоть и имеют разброс в данных, но там не выявляется никакой закономерности). Таким образом, и современные данные наблюдений не позволяют решить вопрос о разделение данных наблюдений древних астрономов по эксцентриситету орбиты Земли на две группы. Но, неужели древние астрономы, использующие экваториальное кольцо и гномон, а также король точности, как его называли, Тихо Браге уже в 17-м веке, используя меридианный круг, просто делали ошибки в своих наблюдениях, а мусульманские астрономы (кроме Аль Хорезми) оказались в своих наблюдениях гораздо точнее их.
Давайте теперь попробуем разобраться логически, как же могло произойти такое разделение значений эксцентриситета орбиты Земли на правильные и не правильные (по перигелию тоже имеется разделение данных на две группы, но не такое явное). А вариантов такого разброса в параметрах орбит может быть только два. Либо сама методика определения параметров орбит по продолжительности сезонов года, которой пользовались до 17-го века, содержит серьезные погрешности, либо имеются большие систематические погрешности в методике определения продолжительности сезонов года. А после 17-го века имеются систематические ошибки или в методике определения параметров эллиптической орбиты по 3-м произвольным наблюдениям или в определение координат Солнца в этих 3-х точках. Здесь надо сказать, что все астрономы до мусульманской эры (включая Аль Хорезми) пользовались методикой расчета параметров орбит, изложенной в Альмагесте, а вот начиная с Аль Баттани пользовались как этой методикой, так и более современной, которая позволяла устранить трудность определения даты летнего солнцестояния. Но у нас большие отклонения от современных значений получились именно для этого промежутка времени, если не считать астрономов XVII века. По этому, имеет смысл хотя бы кратко ознакомиться с этими методиками древних астрономов (более подробно можно почитать в Альмагесте Птолемея или в Каноне Масуда Аль Беруни, но начать лучше с методики Птолемея в современной трактовке в Этюдах по истории планетных теорий Идельсона [6]).
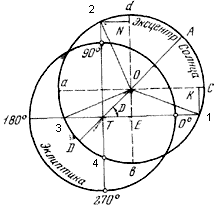
Рис. 5. Схема к методике расчета параметров орбиты Солнца (Земли). Воспроизведено (с изменениями) из работы [6].
Как мы уже знаем, Птолемей для отражения видимого неравномерного движения Солнца вокруг Земли использовал теорию простого эксцентра Гиппарха, которая идентична теории движения эпицикла по дифференту. И хотя теория эксцентра с эквантом была бы поточнее, но в то время такой точности от теории движения Солнца не требовалось. Суть этой теории состоит в том, что Солнце движется равномерно по эксцентру, который смещен относительно центра мира, где находится Земля на величину эксцентриситета эксцентра OT. И теперь, наблюдая из центра эклиптики (мира) T, где находится Земля, за движением Солнца, мы увидим, что в точке афелия Солнца (A) оно движется медленнее, чем в точке перигелия (D). Если мы говорим о гелиоцентрической орбите Земли вокруг Солнца (при движение по кругу эклиптики), то будет происходить тоже самое, только в точке (A) будет находиться перигелий Земли, а в точке (D) афелий. На Рис.5 точкой 1 отмечена точка весеннего равноденствия (начало сезона весны), точкой 2 момент летнего солнцестояния (начало лета), точкой 3 осеннее равноденствие (начало осени) и точкой 4 зимнее солнцестояние (начало зимы).
Расчет положения афелия Солнца и эксцентриситета эксцентра начинается с того, что мы переводим, исходя из продолжительности года, продолжительность сезонов весны (дуга 1-2) и лета (дуга 2-3) в градусную меру. Например, для данных Гиппарха это будет 93,14 и 91,17 градусов. Теперь находим сумму этих углов, вычитаем из нее 180 градусов и делим пополам. Получается 2,156 градуса. Это дуга 1-C. Теперь из угла весны вычитаем угол 90 градусов и найденную дугу 1-C. Получится дуга d-2 равная 0,986 градуса. Если принять радиус эксцентра равным единице, то в этом масштабе отрезки 1-K=O-E и 2-N=T-E будут равны синусам найденных двух дуг. Теперь по теореме Пифагора можем найти гипотенузу T-O, которая и будет равна эксцентриситету эксцентра. А, зная все три стороны треугольника TOE, используя любую тригонометрическую функцию найдем угол 1TA, т.е. долготу афелия. Как видим, ничего сложного здесь нет, но так как мне приходилось многократно пересчитывать различные варианты, я написал специально для этого маленькую программку Ptolemey. А, т.к. все данные у древних астрономов приведены в шестидесятиричной системе счисления, я оснастил ее функцией перевода этих данных в привычную нам десятиричную систему счисления. По этому, если кто-то надумает проверить мои расчеты, то можете скачать программу Ptolemey (вместе с исходниками на языке программирования Visual Basic 6.0.) с зеркала моей домашней страницы здесь http://modsys.narod.ru из раздела Программы.
Как видно из таблицы 3 для тестового расчета в 2000 году эта методика дает некоторую небольшую погрешность, которая равна нулю только в точках, когда афелий или перигелий находятся около точек равноденствий или солнцестояний, но существенно повлиять на результат эта погрешность не может. Более того, если мы учтем погрешность, которую дает эта методика на промежутке от -400 до 2000 годов и проведем на рисунках 3 и 4 рядом с прямыми, отражающими современные теории, еще две прямые с учетом погрешности, которую дает эта методика, то результат будет еще хуже, т.к. в этом случае данные древних астрономов будут еще больше отличаться от современных теорий. Таким образом, сама методика Птолемея для обработки данных наблюдений в разделение данных на две группы ни при чем и остаются только систематические погрешности, связанные с получением экспериментальных данных по продолжительности сезонов года. Для того, чтобы найти эти систематические погрешности, нам надо в первую очередь посмотреть как определялось положение небесного экватора на географической широте fi = 33 градуса северной широты (см. рис. 6).
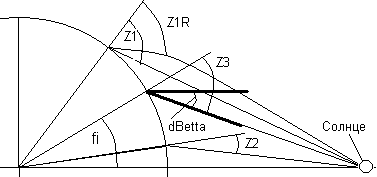
Рис. 6. Схема к расчету положения установки экваториального кольца.
Обратимся к Альмагесту Птолемея, где он пишет, что для этого надо замерить зенитные расстояния в моменты зимнего Z1 и летнего Z2 солнцестояний, а затем взять среднее значение Z3, которое и будет соответствовать положению экватора. Но, как видно из рисунка, это положение экваториального кольца не будет параллельно экватору, а будет немного наклонено к нему под углом dBetta. Расстояние от экватора до плоскости кольца будет H=R3*sin(fi)=6378*sin(33)=3474 км. Отсюда dBetta-= arctg(H/R30)= arctg(3474/150000000)= 0,00133 градуса. Естественно, об этой погрешности знали древние астрономы, т.к. им хорошо было известно, что Земля круглая, и они даже знали примерный ее диаметр по данным Эратосфена. Так Птолемей, описывая различные климатические зоны, пишет, что за 66 параллелью, т.е. за северным полярным кругом, должны наблюдаться полярный день и полярная ночь, а на северном полюсе день и ночь должны длиться по пол года. И это при том, что никаких сведений об этих землях у него не было, а о том, что происходит на 64 параллели он знал только, что там живут неизвестные скифские племена и все.
Но, расстояние до Солнца древние астрономы занизили на порядок, например, Птолемей в 20 раз (1160-1260 радиусов Земли), и по этому, если они и делали поправку на угол dBetta, то наоборот увеличивали погрешность. Дело в том, что они считали, что параллакс Солнца был от 2,3 до 3 угловых минут (сейчас принято 8 угловых секунд). При этом эта погрешность будет не только для экваториального кольца, но и для других астрономических инструментов при переводе топоцентрических горизонтальных координат в геоцентрические экваториальные или эклиптические. К сожалению, я не знаю как было установлено экваториальное кольцо Гиппарха, который выполнил на нем серию наблюдений, по этому я рассмотрю как отразятся на точности определения моментов равноденствий и солнцестояний различные погрешности, возможные при этом. Для этого обратимся к рис. 7 и по нему произведем прикидочный расчет возникающих систематических погрешностей для конкретной географической широты. Если мы возьмем широту 33 градуса, то она будет не более чем на 2…3 градуса отличаться от широты всех мест, где древние астрономы проводили свои наблюдения (кроме Тихо Браге, данные которого использовали Кеплер, Стрит и Винг).
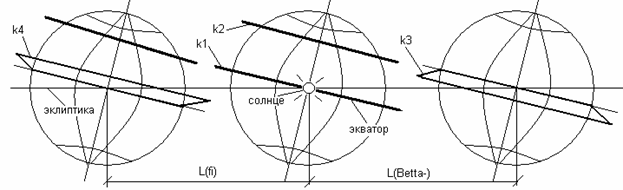
Рис. 7. Схема к расчету систематических погрешностей измерений.
На рисунке в среднем положение мы видим, как будет видна Земля со стороны Солнца в момент весеннего равноденствия (ВР) и, если мы опояшем всю Землю по экватору экваториальным кольцом k1, то в этот момент будут освещаться обе его стороны (северная и южная). Если же мы установим такое кольцо k2 параллельно плоскости экватора, но на широте 33 градуса, то в момент равноденствия из-за параллакса будет продолжать освещаться южная сторона кольца. А для того, чтобы у этого кольца стали освещаться две стороны, Земля должна пройти дальше от точки ВР на расстояние L(fi). Расстояние от экватора до кольца будет H= R3*sin(fi)= 6378*sin(33)= 3474 км. При наклоне экватора к эклиптике под углом 23,5 градуса L(fi)=H/sin(23,5)= 8712 км и с учетом скорости движения Земли равной 29,8 км/с, время запаздывания при фиксации ВР будет dt(H)=L(fi)/V3=8712/29,8=292 сек = +0,00338 дня.
Теперь рассмотрим случай, когда на экваторе в момент ВР находится кольцо k3. Ясно, что в этот момент уже будет освещена северная сторона, а момент, когда будут освещены обе стороны кольца наступит раньше точки ВР. Учитывая, то, что наклон экватора меняется на 23,5 градуса за четверть года, но меняется не равномерно (быстро вблизи точек равноденствия и медленно около солнцестояний) найдем скорость изменения наклона экватора только за 1/8 года вблизи точек равноденствия Vbetta= 23,5*sin(45)*8/365,25= 0,364 град/день. Таким образом, за счет наклона кольца к экватору момент равноденствия будет наступать раньше на dt(Betta-)= dBetta-/Vbetta= 0,00133/0,364= -0,00365 дня. А суммарное запаздывание будет dt(H)+ dt(Betta-)= 0,00365-0,00338= 0,00027 дня = 23 сек, т.е. никакого запаздывания не будет и это только погрешность прикидочного расчета. Что касается моментов летнего солнцестояния (ЛС) и зимнего (ЗС), то ни наклон кольца, ни его высота над плоскостью экватора никак ни отразятся на точности определения этих моментов, т.к. для этих целей используется не экваториальное кольцо, а гномон (вертикальный колышек). А теперь, когда мы поняли, как влияет угол наклона экваториального кольца на погрешность измерения момента равноденствия, давайте рассмотрим более сложный случай с рефракцией и аберрацией.
Как мы видим на рис. 6, зенитное расстояние зимой Z1 будет значительно больше, чем летом Z2 и по этому рефракция будет уже не несколько угловых секунд, как летом, а значительно больше, а по этому погрешность в определение положения экваториального кольца будет значительной. Рефракция при зимнем солнцестоянии будет Ref(Z1)= Ref(33+23,5)= 57,1*tg(56,5)= 0,0249 градуса и, следовательно, после определения Z1 и Z2 мы получим, что положение экваториального кольца получится на половину Ref(Z1) выше, чем мы рассчитали первоначально при отсутствии рефракции (принимаем Ref(Z2) равной нулю). Таким образом, угол dBetta+ будет 0,0249/2-0,00133= 0,01112 градуса и, следовательно, края кольца будут не опущены к экватору, а приподняты вверх. Это приведет к тому, что такое кольцо k4, установленное на экваторе, в момент равноденствия будет продолжать освещаться с южной стороны, и, следовательно, мы будем иметь эффект запаздывания на время dt(Z1)= dBetta+/Vbetta= 0,01112/0,364= 0,03055 дня. Но, если мы это кольцо k4 поместим на широте места наблюдения, то здесь уже появится рефракция в момент наблюдения равноденствий, т.к. Z3 не будет равно нулю, как на экваторе. В этом случае искривленный луч света будет уже заглядывать за край кольца и это даст эффект опережения момента наблюдения. Рефракция в момент наблюдения Ref(Z3)= Ref(33)= 57,1*tg(33)= 0,0103 градуса и, следовательно, dt(Z3)= Ref(Z3)/Vbetta= 0,0103/0,364= -0,0283 дня.
Теперь давайте рассмотрим погрешность определения момента ВР от аберрации. Т.к. мы считаем, что Солнце у нас неподвижно, то, следовательно, планетной аберрации у нас не будет и нам надо учесть только звездную аберрацию. Вообще-то, Солнце у нас не является абсолютно неподвижным и по предварительным данным движется со скоростью 19,4 км/с относительно местной группы звезд, а те со скоростью 225 км/с относительно центра нашей галактики, а тот со скоростью 155 км/с относительно местной группы галактик, а те со скоростью 635 км/с относительно реликтового излучения. Итого получается около 370 км/с, что на порядок больше скоростей, которые мы учитываем, но, как я сказал, во-первых, эти данные приблизительные, а, во-вторых, никто не знает, что делать с этими скоростями, по этому, в современных теориях и при обработке данных наблюдений их никто не учитывает. Таким образом, мы, как и все, учтем только звездную аберрацию от скорости Земли, которая приводит к тому, что источник света мы всегда видим немного дальше по ходу движения, чем он находится на самом деле. И, если мы обратимся к рис.7, то у нас в момент равноденствия свет от Солнца будет падать на Землю немного слева, т.к. Земля у нас движется влево. Это приведет к тому, что в момент равноденствия у нас будет освещаться южная сторона кольца, т.е. будет запаздывание в определении момента равноденствия.
Таким образом, Земле потребуется время dt(A), чтобы пролететь расстояние L(A), аналогично запаздыванию dt(H), где надо было пролететь расстояние L(fi), чтобы свет проходил параллельно плоскости экватора. Находим расстояние L(A)= V3*R30/Vsv= V3*150000000/300000= V3*500 сек и время запаздывания dt(A)=L(A)/V3= V3*500/V3= 500 сек = +0,00578 дня. Теперь, когда мы нашли влияние всех факторов по отдельности на момент фиксации события, давайте просуммируем эти эффекты для нужных нам положений. При этом, надо учесть, что эффект от аберрации всегда будет давать запаздывание, а эффекты от высоты кольца над экватором, наклона кольца и рефракции, при определение времени ОР, будут давать эффект противоположный эффекту при ВР.
dt(ВР)= dt(H) - dt(Betta-) + dt(Z1) – dt(Z2) + dt(A)= 0,00338 - 0,00365 + 0,03055 - 0,0283 -0,00578= - 0,0038 дня = - 5,472 мин
dt(ОР)= dt(H) - dt(Betta-) + dt(Z1) –dt(Z2) + dt(A)= -0,00338 + 0,00365 - 0,03055 + 0,0283 -0,00578= - 0,00776 дня = - 11,174 мин
Следовательно, истинный момент ВР будет на 5,5 мин позже замеренного древними астрономами на экваториальном кольце, а истинный момент ОР будет позже на 11,2 мин. Я даже не стал в соответствие с этими систематическими ошибками наблюдений древних астрономов производить перерасчет получающихся параметров орбиты Земли, т.к. это незначительная погрешность. Правда, в работе [3] говориться, что из-за рефракции у древних астрономов истинный момент ВР будет на 15 минут раньше момента, получившегося из измерений, а для ОР на 15 минут позже, но, к сожалению, я не видел расчетов автора, чтобы судить о том, чьи расчеты верны и даже не знаю о наблюдениях с помощью каких инструментов он пишет, но быстрее всего речь идет о меридианном круге, а не об экваториальном кольце. Хотя и эти 15 минут практически никак не повлияют на параметры орбиты Земли в начале нашей эры, т.к. здесь нужны часы. Более того, если принять, что истинный момент ВР будет на 15 минут раньше, а ОР на 15 минут позже, то на положение перигелия это практически никак не отразиться, а вот эксцентриситет при этом должен увеличиться, т.е. на рис. 3 экспериментальные точки будут еще дальше от современных теоретических значений, т.е. это может только приподнять точки расположенные около прямой 1 (см. рис.4).
Таким образом, мы видим, что и систематические ошибки измерений не позволяют приблизиться данным древних астрономов к данным современных теорий и это тоже не решает загадку их значительного расхождения с данными по современным теориям. Возможен, правда, еще один вариант систематических ошибок измерения – это деформация фундамента и самого экваториального кольца после его установки. Ведь о самих (случайных) ошибках измерения склонения на меридианном круге Птолемей писал, что в то время они могли доходить до 0,1 градуса, что по его словам равносильно ошибке во времени фиксации равноденствия в 0,25 дня, т.е. 6 часов, что мы и видим по округлениям дат равноденствия Гиппархом до 6 часов. И далее он утверждает, что такая случайная ошибка возможна для инструментов, которые постоянно используются для измерений и постоянно подстраиваются по измерениям. А для таких инструментов как экваториальное кольцо ошибка может быть еще больше из-за того, что однажды установленные они могут со временем немного изменять свое положение. И в подтверждение этого он пишет, что особенно это заметно у более большего и древнего медного кольца, т.к., проводя на них измерения, он заметил, что «иногда вогнутые их поверхности одновременно освещаются два раза во время одного равноденствия». Я здесь не совсем понял, что такое вогнутые поверхности, но очевидно это северная и южная стороны кольца.
Вот только, говоря о том, что в наблюдениях такой эффект иногда наблюдался, Птолемей косвенным образом подтвердил, что эти экваториальные кольца были установлены точно хотя бы в одной плоскости, т.к. такой эффект действительно возможен из-за рефракции, но на кольце установленном без бокового крена. Хотя, возможно я здесь ошибаюсь и возможны такие комбинации углов в наклоне кольца к экватору и его бокового крена, а также изменения в течение дня величины рефракции и деформации медного кольца при его нагревание, когда этот эффект тоже будет наблюдаться, но в любом случае это не является явным подтверждением того, что эти кольца были установлены не точно или изменили со временем свое положение. Но все же исключать возможность изменения положений колец у древних астрономов нельзя и, если мы имеем серию наблюдений на одном кольце в течение нескольких лет, то этот эффект можно заметить, т.к., как мы выяснили выше, практически никаких существенных систематических ошибок измерения в наблюдениях на экваториальном кольце быть не должно. При этом, ошибки, вызванные деформацией медного кольца от нагрева Солнцем, следует считать случайными, т.к. деформации кольца утром, днем и вечером будут разные.
В таблицах 5, 6 и 7 я привожу известные мне данные по датам определения летнего солнцестояния (ЛС) и осеннего (ОР) и весеннего (ВР) равноденствий. Причем моменты равноденствий и солнцестояний с помощью экваториального кольца, отверстия в крыше и гномона определялись только где-то до 800 года, а потом только с помощью меридианного круга (в различных вариантах). Из имеющихся у нас данных такой проверке можно подвергнуть только данные Гиппарха, выполненные на экваториальном кольце, т.к., во-первых, они даны для значительного промежутка времени, а, во-вторых, достаточно представительны. Гиппарх приводит даты 6-и ОР и 3-х ВР, а кроме этого он пишет, что еще 11 наблюдений ВР согласовались с приведенными им с избытком в 0,25 дня, что и должно было быть при использовании им календаря без високосных годов.
Вообще-то, работать с данными древних астрономов очень трудно не только из-за применявшейся ими шестидесятиричной системы счисления, но и из-за очень большого разнообразия применявшихся ими календарей. По этому, в таблицах 4, 5 и 6 я привожу не только их даты по Юлианскому календарю (даты до 4.10.1582 г совпадают с современным Григорианским календарем, а затем согласно декрету от 24 февраля папы Григория 13 (1502-1585) обязывалось католикам после четверга 4 октября 1582 года считать следующий день сразу пятницей 15 октября), но и по Египетскому календарю, т.е. по 365 дней в году от 12 часов пополудни эры Набонассара, т.е. от 26.2.725 г. до н.э. и юлианские даты. Даты по Египетскому календарю я привожу по тому, что он используется в таблицах Птолемея и в некоторых расчетах Аль Бируни, а, кроме того, он нам пригодится при рассмотрение данных Гиппарха, т.к., хотя годы (как я понял) он приводит по календарю Калиппа, но дни и месяцы почему-то приведены из Египетского календаря. При этом время (дробная часть дня) я указываю от 0 часов, т.е. от полуночи, как это принято сейчас, а 5 дней в конце года, которые в Египетском календаре не входили ни в один из 12 месяцев по 30 дней, я приплюсовываю к 12-у месяцу (Месоре), а у Гиппарха они считаются 5-ю днями эпагемен.
А использование юлианских дат, которые идут сплошным счетом в днях от 12 часов пополудни 1 января 4713 г до н.э. очень удобно при расчете по датам наблюдений продолжительности сезонов весны и лета, т.к. не надо задумываться сколько дней в конкретном месяце или году. При этом, обращаю Ваше внимание, на то, что когда у меня записан минус первый год, то это 2-ой год до н.э.. Связано это с тем, что нулевого года в Юлианском и Григорианском календарях нет, т.к., когда Дионисий Малый (500-556, Италия) предложил вести счёт годов не от 29 августа 284 г., т.е. возведения на престол Диоклетиана, а от Рождества Христова, т.е. новой эры или Года Господа (Anno Domini), то он просто, как и все европейцы, тогда, не знал нулей и по этому у него после первого года н.э. сразу идет первый год до н.э., но для астрономических вычислений такой год всегда используется (просто в программах пересчета учитывают историческую нелепость).
Таким образом, например, запись ОР от 27 сентября 162 года до н.э. соответствует данным Гиппарха за 30-е Мессоре 17-го года 3-го периода Калиппа, т.е. 30-е Мессоре 586-го года эры Набонассара, а дробная часть даты это время от ноля часов этого дня, которое соответствует указанию Гиппарха, что это событие было в этот день вечером. Этой календарной дате соответствует юлианская дата, отсчитываемая от 12 часов дня по Гринвичскому времени JD=1662522,17, а не 1662522,25, как это соответствует местному времени но острове Родос, где Гиппарх наблюдал это равноденствие. При этом, учитывая то, что при переводе дат наблюдения от одного местного времени к другому, различные авторы использовали очень даже разные значения их географической долготы, я решил использовать некоторые усредненные долготы городов, что с одной стороны вносит погрешность в данные, приведенные конкретным автором, но позволяет хоть как то согласовать между собою данные из различных источников. Конкретно я использовал следующие поправки при переводе местного времени ко всемирному, т.е. ко времени Гринвича : Афины -0,06 дня, Александрия и Родос -0,08, Дамаск, Рака и Самарра -0,1, Джурджания -0,17 и Газна -0,19 дня.
Таблица 5. Данные наблюдений летних солнцестояний.
|
год
|
Автор, город, источник |
Египетский календарь от 0 часов местного времени
|
Юлианский календарь от 0 часов по времени Гринвича |
юлианская дата от 12 часов по времени Гринвича
|
|
-431 |
Метон и Евктемон, Афины, [1] |
21,25.07.316 |
27,19.06.-431 |
1563812,69 |
|
-279 |
Аристарх Самосский, Афины, [1] |
28,75.08.468 |
26,69.06.-279 |
1619330,19 |
|
-134 |
Гиппарх, Родос, [1] |
04,50.10.613 |
26,42.06.-134 |
1672290,92 |
|
140 |
Птолемей, Александрия, [1] |
12,10.12.887 |
24,99.06.140 |
1772368,39 |
|
994 |
Абу Махмуд Ходженди, Багдад, [2,11] |
01,52.07.1742 |
16,80.06.994 |
2084283,30 |
|
1016 |
Аль Бируни, Джурждания, [2] |
07,40.07.1764 |
16,21.06.1016 |
2092318,71 |
|
1900 |
Теория Ньюкома, Лондон |
05,91.02.2649 |
08,91.06.1900 |
2415192,41 |
|
2000 |
Теория JPL, Лондон |
30,07.02.2749 |
08,07.06.2000 |
2451716,57 |
Таблица 6. Данные наблюдений весенних равноденствий.
|
год
|
Автор, город, источник |
Египетский календарь от 0 часов местного времени
|
Юлианский календарь от 0 часов по времени Гринвича |
юлианская дата от 12 часов по времени Гринвича
|
|
-145 |
Неизвестный, Александрия, [1] |
27,46.06.602 |
24,35.03.-145 |
1668178,85 |
|
-145 |
Гиппарх, Родос, [1] |
27,25.06.602 |
24,14.03.-145 |
1668178,64 |
|
-134 |
Гиппарх, Родос, [1] |
30,00.06.613 |
23,89.03.-134 |
1672196,39 |
|
-127 |
Гиппарх, Родос, [1] |
01,75.07.620 |
23,64.03.-127 |
1674753,14 |
|
140 |
Птолемей, Александрия, [1] |
07,54.09.887 |
22,43.03.140 |
1772273,93 |
|
1290 |
Профатиус Юдэус, Франция, [11] |
10,17.06.2038 |
13,17.03.1290 |
2192301,67 |
|
1303 |
Профатиус Юдэус, Франция, [11] |
13,33.06.2051 |
13,33.03.1303 |
2197049,83 |
|
1900 |
Теория Ньюкома, Лондон |
08,07.11.2648 |
08,07.03.1900 |
2415099,57 |
|
2000 |
Теория JPL, Лондон |
02,31.12.2748 |
07,31.03.2000 |
2451623,81 |
Таблица 7. Данные наблюдений осенних равноденствий.
|
год
|
Автор, город, источник |
Египетский календарь от 0 часов местного времени
|
Юлианский календарь от 0 часов по времени Гринвича |
юлианская дата от 12 часов по времени Гринвича
|
|
-161 |
Гиппарх, Родос, [1] |
30,75.12.586 |
27,67.09.-161 |
1662522,17 |
|
-158 |
Гиппарх, Родос, [1] |
31,25.12.589 |
27,17.09.-158 |
1663617,67 |
|
-157 |
Гиппарх, Родос, [1] |
31,50.12.590 |
27,42.09.-157 |
1663982,92 |
|
-146 |
Гиппарх, Родос, [1] |
34,00.12.601 |
26,92.09.-146 |
1668000,42 |
|
-145 |
Гиппарх, Родос, [1] |
34,25.12.602 |
27,17.09.-145 |
1668365,67 |
|
-142 |
Гиппарх, Родос, [1] |
34,75.12.605 |
26,67.09.-142 |
1669461,17 |
|
132 |
Птолемей, Александрия, [1] |
07,51.03.880 |
25,52.09.132 |
1769539,02 |
|
139 |
Птолемей, Александрия, [1] |
08,58.03.887 |
26,22.09.139 |
1772095,72 |
|
829 |
Абу Мансур, Багдад, [2] |
25,53.08.1577 |
19,41.09.829 |
2024111,91 |
|
832 |
Халид Мервази, Дамаск, [2] |
25,97.08.1580 |
18,87.09.832 |
2025207,37 |
|
859 |
Мухаммед и Бану Муса, Самарра, [2] |
02,50.09.1607 |
19,38.09.859 |
2035068,88 |
|
882 |
Аль Баттани, Ракка, [2] |
08,05.09.1630 |
18,95.09.882 |
2043469,45 |
|
888 |
Сулейман ибн Исма, Балх, [2] |
09,58.09.1636 |
18,39.09.888 |
2045660,89 |
|
974 |
Абу Вафа, Багдад, [2] |
29,71.09.1722 |
17,59.09.974 |
2077071,09 |
|
1016 |
Аль Бируни, Джурджания, [2] |
10,54.10.1764 |
17,38.09.1016 |
2092411,88 |
|
1019 |
Аль Бируни, Газна, [2] |
11,29.10.1767 |
18,10.09.1019 |
2093507,60 |
|
1020 |
Аль Бируни, Газна, [2] |
11,50.10.1768 |
17,31.09.1020 |
2093872,81 |
|
1900 |
Теория Ньюкома, Лондон |
09,51.05.2649 |
10,51.09.1900 |
2415286,01 |
|
2000 |
Теория JPL, Лондон |
03,72.06.2749 |
09,72.09.2000 |
2451810,22 |
Давайте построим по этим данным наблюдений графики, чтобы наглядно посмотреть всю картину того, как у нас изменяются продолжительности сезонов года. Ведь если бы древние астрономы умели строить графики, то Гиппарх наверняка бы заметил, что с его датами ОР не все в порядке. Здесь надо сразу сказать, что и с интерпретацией данных наблюдений Гиппарха и Птолемея тоже не все так однозначно. Например, Стрит вообще по тексту Альмагеста понял, что Гиппарх все свои наблюдения производил в Александрии и дату его первого ВР определил по наблюдению неизвестного астронома (см. таблицу 6). А Аль Бируни почему-то определил дату его 2-го наблюдения ОР на день позже. Я уже не говорю о том, что обе даты ОР Птолемея у него получились в таблице, содержащей даты ОР на 240 дней позже. Причем это не просто описка, т.к. эта ошибка дублируется и в соседней колонке при другом расчете. А с другой стороны Аль Бируни на нескольких страницах, показывая незаурядные познания в календарях, доказывает, что Птолемей на несколько часов указал не правильно продолжительность сезонов года из-за того, что даты наблюдения ВР, ЛС и ОР, которые он берет подряд, при том календаре, что он использовал, попадают в другой год.
Отсюда надо сделать вывод, что к данным, которые приводят древние астрономы (или их соратники переписчики и переводчики) надо относиться очень осторожно. По этому, давайте не будем использовать уже готовую табличку данных Гиппарха и Птолемея, кочующую из одного издания в другое, а попытаемся сами определить даты их наблюдений используя доставшийся нам текст Альмагеста (подлинник утерян). Начнем с данных Гиппарха и воспроизведем его даты сначала в Египетском календаре (см. рис.8), что будет больше соответствовать тексту оригинала, который в Альмагесте выглядит для ОР так «В 17 году 3-го периода Калиппа при заходе Солнца, затем через 3 года, в 20 году, в первый день эпагомен утром, когда оно долженствовало быть в полдень, так что получается разница в ¼ часть дня. Через 1 год, в 21 году [равноденствие наблюдалось] в 6 часов, что согласовалось с предыдущим наблюдением. Через 11 лет, в 32 году оно было в полночь с 3-го на 4-й день эпагомен, а долженствовало быть утром, так что опять получилась разница в ¼ дня. Через 1 год, в 33 году, в 4-й день эпагомен оно было утром, что также было согласно с предыдущим наблюдением. Через 3 года, в 36 году, в 4-й день эпагомен оно было вечером, а должно было быть в полночь, так что опять получается разница в ¼ [дня].»
И для ВР так «В 32 году третьего периода Калиппа 27 Мехира утром. И круг, говорит он, который в Александрии, был одинаково освещен с обоих сторон около 5-го часа. Таким образом, уже различные наблюдения одного и того же равноденствия дали разницу приблизительно в 5 часов. А следующие, говорит он, вплоть до 37 года согласовались с избытком в ¼ дня. А через 11 лет [после наблюдения в 32 году], в 43 году, 29 Мехира после полуночи, предшествующей 30-му, он говорит было весеннее равноденствие, которое соответствовало наблюдению в 32 году. Как он утверждает, оно опять согласовалось с наблюдениями последних лет вплоть до 50 года. Тогда оно произошло в первый день Фаменота около захода Солнца приблизительно на 1 1/2 ¼ день позже, чем в 43 году, что согласуется с 7 предыдущими годами».
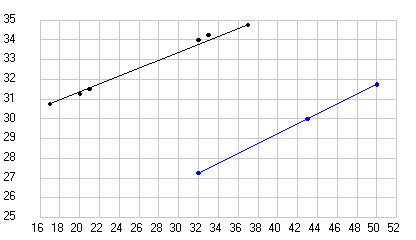
Рис. 8. Моменты весеннего и осеннего равноденствий Гиппарха в Египетском календаре.
Здесь надо дать некоторые пояснения для людей не знакомых с исчислением времени у древних астрономов. Когда Гиппарх говорит об утре или вечере, то это по современному будет 6 часов и 18, т.к. при равноденствиях день примерно равен ночи. Это же обстоятельство облегчает нам и расчет времени, когда оно дается в часах. Дело в том, что у древних астрономов весь день и вся ночь всегда были равны 12 часам не зависимо от того летняя это ночь (8 часов) или зимняя (16 часов) и, соответственно, для дней. Но в нашем случае мы будем иметь 12 астрономических часов равных 12 реальным часам и, когда Гиппарх говорит, что 3-е ОР было в 6 часов, то это значит, что оно было по прошествии 6 часов дня, т.е. по нашему в 12 часов. Если принять это во внимание, то данные на рис.8 полностью соответствуют описанию в Альмагесте, но по ним трудно увидеть в чем причина такого не соответствия ОР. А вот в датах Юлианского календаря на рис.9 видно, что первые три наблюдения ОР явно не согласуются с 3-мя последними.
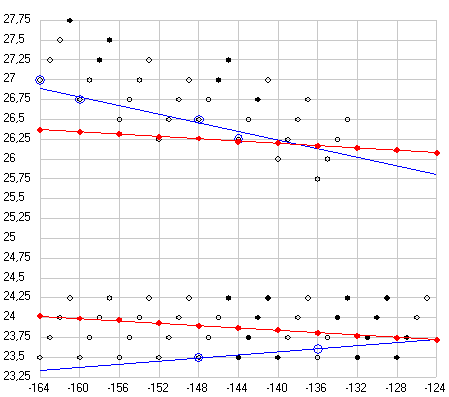
Рис. 9. Моменты весеннего и осеннего равноденствий Гиппарха в Юлианском календаре (точки - экспериментальные данные, кружки - аппроксимация, красная линия – даты в високосные годы по теории Ньюкома).
Как мы видим, данные ВР имеют очень хорошую повторяемость, в соответствие с Юлианским календарем, и мы можем легко достроить недостающие точки для любого нужного нам года, а вот данные ОР однозначно не интерпретируются. Ведь по первым трем наблюдениям мы имеем один график изменения моментов ОР, а по трем вторым наблюдениям другой. Возможно, это связано с тем, что как пишут многие авторы, три первых наблюдения сделаны не Гиппархом, а может быть даже и на другом экваториальном кольце, а может быть это вызвано какими то нелинейными систематическими ошибками. Т.е. из тех данных, что Гиппарх приводит, можно из различных предположений получить совершенно разные данные.
Да, случайные ошибки у древних астрономов, конечно же, были, но, судя по данным Гиппарха, они составляли не более нескольких часов, а по расчетам [8] они должны были для согласия с современными теориями составлять для момента ВР -0,49 дня, а для момента ОР -0,15 дня (при отсутствие ошибки в моменте ЛС). Да, в этом случае мы получим AlfaP=66,0345 и Eks=0,01758, что соответствует современным данным, но в таком случае это уже будут не случайные ошибки, а систематические, т.к. у них должен быть строго заданный знак отклонения. А, учитывая, то, что знак здесь должен быть один и тот же, такие ошибки не могут быть и систематическими, т.к. отклонения в положение экваториального кольца для ВР и ОР приводят к противоположному эффекту. Таким образом, ни случайные ошибки, ни систематические ошибки в наблюдениях Гиппарха не позволяют согласовать его данные наблюдений с современными теориями, но с другой стороны его данные в том виде, как мы их изобразили на графике, плохо согласуются и между собою.
Можно, правда, предположить, что нестыковка в датах ОР вызвана всего-навсего округлением Гиппархом даты до четверти дня, а это целых 6 часов., т.е. с допуском +/- 3 часа. Если мы примем эту гипотезу и проведем прямую между двумя первыми високосными годами 3-х первых наблюдений и двумя вторыми високосными годами 3-х вторых наблюдений, то мы согласуем первые 3-и наблюдения со вторыми 3-я при максимальной ошибке в датах менее 1/8 дня, т.е. уложимся в интервал округлений, которым пользовался Гиппарх. Но отсюда сразу становится ясно, что даты ОР уменьшаются явно быстрее, чем это следует из современных теорий (см. красную линию, которая отражает даты в високосные годы). И на интервале от -164 года до -124 года эта разница составит 0,78 дня, что может быть объяснено только деформацией фундамента под южной опорой экваториального кольца. В результате у нас при ОР южная сторона кольца освещается все позже и позже. Но ведь подобный эффект должен был наблюдаться и при ВР, когда северная сторона кольца должна была освещаться все раньше и раньше. И действительно по данным ВР такой эффект наблюдается, но скорость деформации фундамента получается в 2 раза меньше, если не учитывать замечания Гиппарха о том, что ВР в -134 году было не ровно в полночь, а после полуночи и последнее наблюдение было быстрее всего после захода Солнца, а не просто около захода Солнца примерно через 1,75 дня, как пишет Гиппарх, т.к. если бы он успел его зафиксировать до захода Солнца, то он бы так и написал, что оно было до захода Солнца.
Интересно отметить и то, что первое наблюдение в -145 году было утром, но явно зафиксировать момент ВР Гиппарх мог только когда Солнце уже взошло, т.е. осветило кольцо, по этому, весьма вероятно, что сам момент наступил еще до того, как Солнце осветило кольцо. Но оставим первое наблюдение на месте, а вот второе наблюдение в -134 году, при допуске Гиппарха в 3 часа, мы можем спокойно перенести на 2 часа позже полуночи. В таком случае у нас получается, что опережение ВР с -164 по -124 годы составит 0,69 дня, т.е. получится примерно то же самое, что и при ОР. И истинные значения ОР и ВР должны получиться только в момент установки экваториального кольца, когда деформации фундамента еще не было. Судя по датам наблюдений можно предположить, что это было не раньше -161 года, но, чтобы согласовать данные наблюдений различных авторов, мы будем приводить их только для високосных годов и в таблицу ниже запишем по две точки ВР и ОР для -164 и -124 годов.
А, что касается данных наблюдений самого Птолемея, то по их описанию в Альмагесте они хорошо идентифицируются и разночтений с современной трактовкой этих дат у меня нет. Вызывает правда некоторое подозрение высокая точность в определение моментов ВР, ОР и ЛС, которая составляет у него около часа, что, по моему мнению, очень высокая точность для равноденствий, определенных на экваториальном кольце, и для ЛС, определенного по гномону на широте Александрии, где тень очень короткая. Но к анализу данных Птолемея, а также приведенных им дат ЛС Метона с Евктимоном и Аристарха Самосского, где как выяснится вопросов больше, чем по данным Гиппарха, мы вернемся позже, после того как нанесем на один график и данные наблюдений всех остальных астрономов. При этом, мы так же, как и с датами Гиппарха, приведем их к ближайшему високосному году, чтобы не было ошибки из-за смещения дат равноденствий по Юлианскому календарю от года к году на 0,25 дня. А кроме этого в таблицах 5*, 6* и 7* дополним данные таблиц 5, 6 и 7 еще и расчетными датами, полученными по наблюдаемому равноденствию и по приведенной авторами продолжительности сезонов года (такие даты в таблицах я буду отмечать звездочкой).
Таблица 5* Даты летних солнцестояний в високосные годы
|
Год и автор |
Пересчет или расчет даты наблюдения |
|
-432 Метон и Евктимон |
27,19.06.-431 – 0,25 = 26,94.06.-432 |
|
-280 Аристарх Самосский |
26,69.06.-279 – 0,25 = 26,44.06.-280 |
|
-132 Гиппарх |
26,42.06.-134 – 0,5 = 25,92.06.-132 |
|
140 Птолемей |
24,99.06.140 = 24,99.06.140 |
|
832* Халид Мервази |
18,87.09.832 – 93,16 = 17,71.06.832 |
|
860* Бану Муса |
18,63.09.860 – 93,02 = 17,61.06.860 |
|
880* Аль Баттани |
18,45.09.880 – 93,03 = 17,42.06.880 |
|
888* Сулейман ибн Исма |
18,39.09.888 – 93,04 = 17,35.06.888 |
|
972* Абу Вафа |
17,09.09.972 – 93,12 = 15,97.06.972 |
|
1016 Аль Бируни |
16,21.06.1016 = 16,21.06.1016 |
|
1900 теория Нькома |
08,91.06.1900 = 08,91.06.1900 |
|
2000 теория JPL |
08,07.06.2000 = 08,07.06.2000 |
Таблица 6* Даты весенних равноденствий в високосные годы
|
Год и автор |
Пересчет или расчет даты наблюдения |
|
-164* Гиппарх |
23,25.03.-164 с графика на рис. 9 по Гринвичу |
|
-124* Гиппарх |
23,65.03.-124 с графика на рис. 9 по Гринвичу |
|
140 Птолемей |
22,43.03.140 = 22,43.03.140 |
|
832* Халид Мервази |
18,87.09.832 – 187,07 = 15,80.03.832 |
|
860* Бану Маса |
19,38.09.859 – 0,75 = 18,63.09.860 -186,71 = 15,92.03.860 |
|
880* Аль Баттани |
18,95.09.882 – 0,50 = 18,45.09.880 -186,61 = 15,84.03.880 |
|
888* Сулейман ибн Исма |
18,39.09.888 – 18б,5 = 15,89.03.888 |
|
972* Абу Вафа |
17,59.09.974 – 0,50 = 17,09.09.972 – 186,62 = 14,47.03.972 |
|
1016* Аль Бируни |
17,38.09.1016 – 186,52 = 14,86.03.1016 |
|
1020* Аль Бируни |
17,31.09.1020 – 186,52 = 14,79.03.1020 |
|
1288 Профатиус Юдэус |
13,17.03.1290 – 0,50 = 12,67.03.1288 |
|
1304 Профатиус Юдэус |
13,33.03.1303 – 0,75 = 12,58.03.1304 |
|
1900 теория Ньюкома |
08,07.03.1900 = 08,07.03.1900 |
|
2000 теория JPL |
07,31.03.2000 = 07,31.03.2000 |
Таблица 7* Даты осенних равноденствий в високосные годы
|
Год и Автор |
Пересчет или расчет даты наблюдения |
|
-164* Гиппарх |
26,81.09.-164 с графика на рис. 9 по Гринвичу |
|
-124* Гиппарх |
25,72.09.-124 с графика на рис. 9 по Гринвичу |
|
132 Птолемей |
25,52.09.132 = 25,52.09.132 |
|
140 Птолемей |
26,22.09.139 – 0,75 = 25,47.09.140 |
|
828 Абу Мансур |
19,41.09.829 – 0,25 = 19,16.09.828 |
|
832 Халид Мервази |
18,87.09.832 = 18,87.09.832 |
|
860 Бану Муса |
19,38.09.859 – 0,75 = 18,63.09.860 |
|
880 Аль Баттани |
18,95.09.882 – 0,50 = 18,45.09.880 |
|
888 Сулейман ибн Исма |
18,39.09.888 = 18,39.09.888 |
|
972 Абу Вафа |
17,59.09.974 – 0,50 = 17,09.09.972 |
|
1016 Аль Бируни |
17,38.09.1016 = 17,38.09.1016 |
|
1020 Аль Бируни |
17,31.09.1020 = 17,31.09.1020 |
|
1900 теория Ньюкома |
10,51.09.1900 = 10,51.09.1900 |
|
2000 теория JPL |
09,72.09.2000 = 09,72.09.2000 |
Теперь выведем все эти даты на один график (Рис.10) и аппроксимируем (на глаз) даты ВР, ЛС и ОР прямыми линиями, не забывая о том, что в двух датах Гиппарха (-164 и -124 годы) мы должны проводить линию ближе к первым точкам. Но, прежде чем приступить к анализу получающихся зависимостей, я хочу прокомментировать то обстоятельство, что данные Абу Вафы я продублировал со сдвигом в пол дня, т.к. по тем данным, что приводит Аль Бируни, получается, что продолжительности сезонов Абу Вафа определил правильно, а дату своего ОР привел не правильно. Я не знаю, чья тут ошибка (или описка) Абу Вафы или Аль Бируни, но, я считаю, что дату ОР, которую приводит Аль Бируни, я интерпретировал правильно. Даты всех ОР Аль Бируни приводит в таблице, где он сначала дает долготы всех городов, где были сделаны эти наблюдения, затем указывает время наблюдения (день или ночь) и день недели, когда было сделано наблюдение, дату и месяц (по месяцам персов и по месяцам коптов) и неполный год наблюдения по эре Набонассара, т.е. текущий год. А далее в этой таблице он указывает время наблюдения по эре Набонассара приведенное к долготе Газны и началу суток от полудня в годах и сутках (получается что то наподобие юлианских дат).
Так вот от эры Набонассара до наблюдения Абу Вафы, как он пишет, прошел 1721 год и 268,276 суток. Давайте рассчитаем юлианскую дату этого наблюдения JD=JD0+1721*365+268,276 = 2077071,276, где JD0 = 1448638,0 это юлианская дата 1 тот (по нашему январь) 1 года эры Набонассара. Теперь отсюда легко найти, что это было 30,276.09.1722 года эры Набонассара и 18,276.09.974 года нашей эры (время я пока даю от 12 часов дня текущего дня, т.е. так, как это было принято до 20-го века), что соответствует сделанным мною записям в таблице 7 с учетом разницы во времени между Багдадом и Газной и Лондоном и Газной. Таким образом получается, что Абу Вафа наблюдал это равноденствие в Багдаде 30 пахона 1722 года, что соответствует указанию Аль Бируни в начале таблицы, где он также сообщает, что это было дневное время суток пятницы. Конкретно у нас получится, с учетом разницы во времени между Багдадом и Газной, что после полудня 30 пахона прошло 0,206 суток, т.е. примерно 5 часов после полудни, а ночь наступает в 6 часов после полудни. Таким образом, полученная мною дата наблюдения полностью соответствует всем данным о ней Аль Бируни.
А продолжительности сезонов, полученные разными астрономами, Аль Бируни дает в Каноне Масуда просто в сутках (без указания дат наблюдения) по этому в этих данных, часть из которых дана в таблице 2, я ошибиться не мог. Следовательно, и даты ВР и ЛС Абу Вафы я вычислил правильно (см. таблицы 6* и 7*). Но, как мы видим, все три точки Абу Вафы хорошо согласуются с данными всех остальных астрономов, только при условии, что дата осеннего наблюдения была на пол дня позже. Просто ошибиться во времени дня ни Абу Вафа ни Аль Бируни не могли и по этому такое расхождение во времени наблюдения я могу объяснить только тем, что или Абу Вафа или Аль Бируни просто указали не тот год наблюдения. Если мы примем, что это был 972 или 976 год, т.е. високосный год, то все встанет на свои места, т.к. разница во времени наблюдения ОР между этими годами и 974 годом как раз и будет плюс пол дня. Хотя может быть такое смещение вызвано и не правильным учетом параллакса Солнца (пояснения см. ниже).
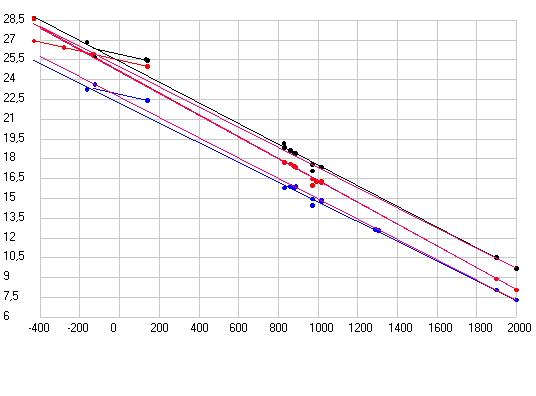
Рис.10. Даты наблюдения весенних (синие точки) и осенних (черные точки) равноденствий и летнего солнцестояния (красные точки) древних и современных астрономов в датах Юлианского календаря, а две серые прямые это аппроксимация дат ВР и ОР рассчитанных по теории Ньюкома.
Я думаю, что, если бы древние астрономы умели строить графики, то Аль Бируни сразу бы заметил эту нестыковку с датой ОР Абу Вафы, точно также как Гиппарх бы заметил нестыковку в датах своих ОР. Но при этом бы и все астрономы обратили внимание на странные даты ВР, ЛС и ОР Птолемея, которые хорошо согласуются с датами наблюдений Гиппарха, но странным образом смещены на 0,93 суток, что практически не возможно объяснить ошибками наблюдения при использовании тех инструментов, которыми пользовался Птолемей. А, как он пишет, для этого он использовал описанные им инструменты (экваториальное кольцо, гномон, меридианный круг и квадрант). А если мы посмотрим на даты 4-х наблюдений ЛС, приведенных Птолемеем, то сразу возникает мысль обратиться в детективное агентство для расследования того, как эти 4-е наблюдения из которых три не правильные ухитрились просто идеально лечь на одну прямую с принятой Гиппархом продолжительностью года равной 365,25 -1/300. Я, например, кроме как фальсификацией данных наблюдений все это объяснить не могу.
Конечно же, утверждать с полной уверенностью, что первым физиком-теоретиком (я их называю математико-физиками или матфизиками, а их теории математической физикой или матфизикой, по тому, что на первом месте у них математика, а потом уже все остальное и в том числе здравый смысл и совесть) был не Макс Планк, а Птолемей из-за недостаточности независимых данных того времени я не могу, но приведенные им данные наблюдений и некоторые его комментарии наталкивают на такое утверждение. Например, он пишет «Теперь, что касается древности [наблюдений], то следовало бы сравнить данные наблюдения летнего солнцеворота, проведенных Метоном и Евктемоном, а также проведенных после них Аристархом с нашими. Однако вследствие того, что наблюдения солнцеворотов не являются достаточно точными и, кроме того, данные упомянутых лиц должны рассматриваться лишь как приблизительные (так по видимому думал и Гиппарх), мы опустили их. Для предложенного сравнения мы взяли наблюдения равноденствий, а из них, ради их большей точности, - сделанные Гиппархом, а именно те, которые он считал наиболее надежными».
Однако, уже на следующей странице мы видим, что он использует эти данные для подтверждения верности своих наблюдений, а именно он пишет «И если мы из-за древности сравним данные наших наблюдений, вычисленных с наибольшей точностью, с данными летнего солнцеворота, полученными Метоном и Евктемоном (записанными довольно поверхностно), то мы получим то же самое». Не понятно только почему Птолемей считает эти данные записанными довольно поверхностно. Ведь у Аль Бируни (кстати, со ссылкой на Альмагест) написано, что «Они наблюдали его утром в воскресенье двадцать первого дня седьмого месяца коптов в триста шестнадцатом году Набонассара». А про наблюдение Аристарха Аль Бируни пишет «[Это] было на закате Солнца в воскресенье двадцать восьмого [дня] восьмого месяца четыреста [шестьдесят] восьмого года. Т.е. точность описания этих солнцестояний точно такая же, как и у Гиппарха, описания наблюдений которого я приводил выше и которые он считает полными.
И потом, если до наших дней дошли сведения о продолжительности сезонов года Метона и Евктемона, то они, равно как и сами даты наблюдения равноденствий, конечно же, были в распоряжение Птолемея. Ведь в то время в Александрийской библиотеке, где работал Птолемей, были работы практически всех ученых. По этому, не понятно кто мешал Птолемею использовать даты равноденствий Метона и Евктемона, если он считал даты солнцестояний не точными. Ведь, если предположить, что Метон и Евктемон определили даты равноденствий в соответствие с нашей аппроксимацией данных на рис. 10, то, рассчитав по их продолжительностям сезонов года (см. таблицу 2) две даты ЛС от ВР = 28,49 и от ОР = 28,80, а потом, взяв среднее значение, мы получим дату 28,645.06.-432 года, которая хорошо согласуется с нашей аппроксимацией (на рис. 10 красный квадрат). Так что доводов в пользу того, что Птолемей, как настоящий математико-физик просто рассчитал свои даты наблюдений предостаточно.
Но, быстрее всего, Птолемей действительно производил наблюдения, но получил другие данные, которые приводили к тому, что афелий Солнца сместился относительно положения Гиппарха. А, если в его распоряжение были и очень противоречивые для того отрезка времени данные Калиппа и Вавилонских астрономов (а они обязательно должны были у него быть), то единственным разумным решением в такой ситуации было принять, что афелий со времен Гиппарха не переместился. Очевидно, по этому, он и заговорил в Альмагесте о возможных ошибках в определение равноденствий, а свои даты просто рассчитал по данным Гиппарха, т.к. астрономом-практиком он был не очень хороший, а в квалификации Гиппарха он не сомневался. А, после принятия такого решения, он даже не стал определять по данным своих же собственных наблюдений продолжительность сезонов года, а принял ее для расчета параметров орбиты Солнца такой, как она получилась у Гиппарха.
А, если мы еще вспомним и координаты звезд, которые Птолемей приводит в своем звездном каталоге, где ясно видно, что эти координаты получены просто пересчетом (с учетом принятой им прецессии) координат, приведенных Гиппархом, то станет ясно, что для аппроксимации дат наблюдения данные Птолемея использовать категорически нельзя. А в этом свете и даты ЛС Метона и Евктемона, а также Аристарха (взятые нами из работы Птолемея) из выборки следует исключить. Тогда мы получим следующие зависимости для ВР, ЛС и ОР по Гринвичскому времени, где дробная часть дня это время от 0 часов этого дня, как это принято сейчас.
ВР = 7,31 – 0,74750 * dT
ЛС = 8,069 – 0,83046 * dT
ОР = 9,719 – 0,78463 * dT
Где dT = (JD – J2000) / 36525 – время в столетиях от юлианской даты наблюдения до юлианской даты стандартной эпохи J2000 (можно вычислять и в годах, как год наблюдения минус 2000 год и все это деленное на сто).
Предвидя возможные замечания о том, что зависимости дат ВР и ОР полученные из современных теорий идут почти параллельно (разница между датами в -400 году и 2000 году составляет, соответственно, 18,30 дня и 18,47 дня), а полученные мною зависимости явно не параллельны друг другу (разница получается 17,94 и 18,83 дня), и, следовательно, зависимости в современных теориях более точные, чем мои, отвечу заранее, что эти две прямые и не должны быть параллельными. Это было бы возможно только в том случае, если бы орбита Земли была окружностью и тогда скорость движения Земли по орбите была бы одинаковой и весной и осенью. А при движение по эллипсу она постоянно изменяется и зависит, как от величины эксцентриситета, так и от угла поворота эллипса в плоскости эклиптики, т.е. от долготы перигелия, которые изменяются и по современным теориям и изменялись по теориям древних астрономов. И на рисунке 10* я привожу зависимость изменения дат равноденствий в -400 году при разных значениях эксцентриситета орбиты Земли, где видно, что чем будет больше эксцентриситет орбиты Земли, тем больше будет неравномерность угловой скорости Земли по орбите. При этом, две зависимости дат ВР и ОР будут все дальше отстоять друг от друга на рис.10, т.к. при этом даты ВР будут уменьшаться, а ОР увеличиваться.

Рис.10* Зависимость дат ВР (синие точки) и ОР (черные точки, а 36 сентября на графике это 6 октября) в 401 году до н.э. от величины эксцентриситета (увеличен в 100 раз), где даты рассчитаны по теории Ньюкома с фиксированными значениями эксцентриситета.
Аналогичное влияние на смещение дат равноденствий будет оказывать и поворот эллипса, т.е. смещение его перигелия, т.к. точки ВР и ОР, расположенные на оси Х (см. рис. 1 и 5) будут одна приближаться к перигелию (ОР), а другая удаляться (ВР) при начальном значение AlfaP=62 градуса и, следовательно, скорость движения Земли будет в одном случае увеличиваться, а в другом уменьшаться. Следовательно, истинностью этих двух зависимостей изменения дат равноденствий (по теории Ньюкома и полученных мною) следует считать не их максимальную параллельность, а их максимальное приближение к экспериментальным точкам. Хотя, возможно, что прямая ОР и должна пройти немного ближе к прямой полученной по теории Ньюкома, т.к. даты исламских астрономов все таки лежат ниже полученной мною зависимости, но это не принципиально. По этому, давайте сейчас, используя уже полученные мною зависимости дат ВР и ОР, рассчитаем усредненные значения продолжительностей сезонов года, а по ним, используя методику Птолемея, параметры орбиты Земли и все эти данные поместим в таблицу 8. А затем, дополним параметры орбит на рис. 3 и рис. 4 этими усредненными параметрами орбит (рис. 3* и рис. 4*).
Весна = 92,759 + 0,045833 * dT
Лето = 93,650 – 0,082958 * dT
Таблица 8. Расчетные значения продолжительности сезонов года и полученные по этим значениям параметры орбиты Земли.
|
год |
dT |
весна |
Лето |
AlfaP |
Eks |
|
-400 |
-24 |
94,750 |
92,550 |
64,79 |
0,022215 |
|
-200 |
-22 |
94,584 |
92,642 |
67,11 |
0,021473 |
|
0 |
-20 |
94,418 |
92,733 |
69,58 |
0,020765 |
|
200 |
-18 |
94,252 |
92,825 |
72,22 |
0,020101 |
|
400 |
-16 |
94,086 |
92,917 |
75,05 |
0,019483 |
|
600 |
-14 |
93,920 |
93,008 |
78,03 |
0,018912 |
|
800 |
-12 |
93,755 |
93,100 |
81,20 |
0,018404 |
|
1000 |
-10 |
93,589 |
93,192 |
84,54 |
0,017951 |
|
1200 |
-8 |
93,423 |
93,283 |
88,03 |
0,017558 |
|
1400 |
-6 |
93,257 |
93,375 |
91,69 |
0,017237 |
|
1600 |
-4 |
93,091 |
93,467 |
95,46 |
0,016988 |
|
1800 |
-2 |
92,925 |
93,558 |
99,32 |
0,016811 |
|
2000 |
0 |
92,759 |
93,650 |
103,25 |
0,016716 |
|
2200 |
2 |
92,593 |
93,742 |
107,21 |
0,016700 |
|
2400 |
4 |
92,427 |
93,833 |
111,15 |
0,016759 |
|
2600 |
6 |
92,261 |
93,925 |
115,05 |
0,016902 |
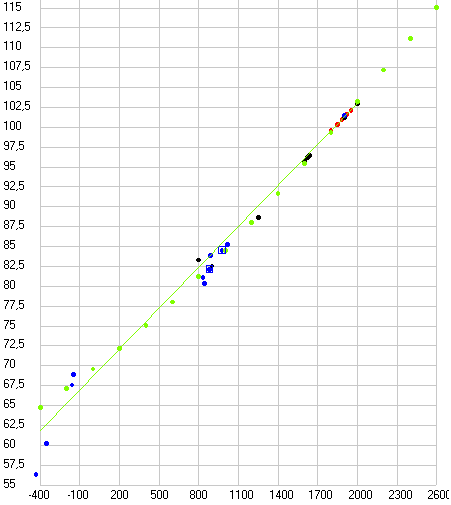
Рис.3* Долгота перигелия орбиты Земли по данным таблиц древних астрономов и двум современным теориям (черные точки), рассчитанная по продолжительности сезонов (синие точки), полученная при обработке данных различных обсерваторий с 1800 по 1983 годы (красные точки) и светло зеленые точки – по данным таблицы 8 (прямая линия построена по теории JPL0).
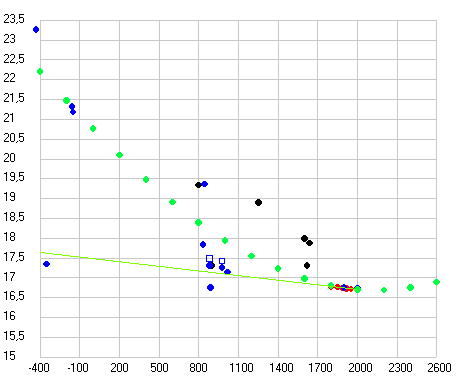
Рис. 4* Эксцентриситет орбиты Земли (увеличено в 1000 раз) по данным таблиц древних астрономов и двум современным теориям (черные точки), рассчитанный по продолжительности сезонов (синие точки), полученный при обработке данных различных обсерваторий с 1800 по 1983 годы (красные точки) и светло зеленые точки – по данным таблицы 8 (прямая линия построена по теории JPL0).
Как видим, теперь все становится на свои места и получается, что данные древних астрономов не противоречат современным данным, но получается, что данные мусульманских астрономов отклоняются от расчетных данных в одну сторону, а европейских в другую. Теперь, попробуем решить и эту загадку, а начнем мы с более подробного ознакомления с методиками исламских астрономов и с полученными ими данными наблюдений. Рассмотрим экспериментальные данные с 833 года по 1020 год, которые приводит Аль Бируни в Каноне Масуда (ссылку дать не могу, т.к. в Интернете этой работы и даже 6-ой книги Канона Масуда, где рассматривается этот вопрос, нет). Правда, он не приводит данных непосредственных измерений, а только уже получившиеся окончательные результаты и в основном по продолжительности сезонов года. Более того, Аль Бируни, скажем так, очень произвольно обращается с экспериментальными данными продолжительностей сезонов года, не говоря уже о том, что в его расчетах постоянно возникают подозрительные арифметические ошибки.

Рис. 11. Хронология жизни исламских астрономов (воспроизведено из работы [8])
Например, он указывает полученную им продолжительность сезонов весны и лета 93,446 дня и 93,05 дня, и несколькими страницами позже подтверждает эти данные, указав суммарную их продолжительность, но в своем расчете он использует эту продолжительность весны и совсем другую продолжительность лета. Это, правда, одна из немногих (таких как дата 2-го ОР Гиппарха или даты ОР Птолемея) грубая арифметическая ошибка, которую я заметил, а основная масса ошибок в его расчетах связана, быстрее всего, или с погрешностями используемых им тригонометрических таблиц или с методикой определения расчетной продолжительности года. Так, например, из-за неясности в расчетной продолжительности года в расчете параметров орбиты Солнца у Аль Бируни по одним и тем же данным Птолемея (Гиппарха) в Хронологии получился результат AlfaA=65,44154 и Eks2=0,041387 , а в Каноне Масуда AlfaA=65,45212 и Eks2=0,039901 (комментарии к работам Аль Бируни можно посмотреть здесь [9]).
Или возьмем пример с использованием данных Бану Мусы. Он указывает найденные им длительности сезонов весны, весны+лета и осени+зимы. Отсюда легко найти для расчета параметров орбиты Солнца продолжительности и всего года и лета, но он идет другим путем. Он задается продолжительностью всего года 365,25 дня, затем вычитает сезоны осень+зима и находит сезоны весна+лето, а затем уже, вычитая сезон весны, находит сезон лета. Согласитесь, что методологически верно было бы из уже известного сезона весна+лето вычесть весну и найти лето, а продолжительность года в расчетах использовать опять таки согласующуюся с экспериментальными данными.
Такая же неясность в расчетах у него и при обработке данных Сулеймана, где известны экспериментальные продолжительности всех сезонов и года целиком, но он использует продолжительности сезонов весны и лета экспериментальные, а продолжительность года теоретическую. При этом в разных вариантах расчета получаются немного другие данные. Сравните результаты по расчету Аль Бируни с результатами, которые получаются при использование только экспериментальных данных Бану Мусы и Сулеймана (в таблице 3 это расчеты 2). Да, основная масса различных ошибок в его расчетах не приводит к большим отклонениям в полученных значениях параметров орбиты Солнца, но при этом меня настораживает то обстоятельство, что все эти ошибки, почему-то, всегда приводят к одному результату, т.е. к увеличению полученного значения долготы афелия Солнца, смещение которого Аль Бируни и доказывал. Посмотрите таблицу 3, где я привожу рассчитанные мною по данным Аль Бируни значения параметров орбит и в знаменателе (со звездочкой) привожу значения, полученные самим Аль Бируни по этим же данным.
По этому, я очень настороженно отношусь к данным исламских астрономов, которые приводит Аль Бируни. И, если ознакомится с работами Морозова, Фоменко и Постникова, где они не совсем бесспорно утверждают даже то, что почти все работы и почти до 14-го века являются подделками более позднего времени, то эта настороженность только усилится, т.к. их замечания по некоторым работам являются очень весомыми. Но, если, все же, считать, что Канон Масуда не подделка, то и здесь я считаю, что, задавшись целью сдвинуть афелий Солнца, Аль Бируни предвзято относился к экспериментальным данным различных авторов. И в Каноне Масуда он приводит только данные тех авторов, которые подтверждают его теорию о смещение афелия. Доказательством этого может служить, например, то, что несколькими годами раньше у него в распоряжение были те же самые данные наблюдений, а он в своей Хронологии писал, что «… перемещение апогея подтверждается наблюдениями одних ученых, равно как отрицается наблюдениями других. Я говорю это не для отрицания /перемещения апогея/, а чтобы напомнить о /неясной/ сути его обстоятельств». Так почему же мы не видим в Каноне Масуда данных, которые бы отрицали перемещение афелия Солнца. Более того, теперь он пишет, что у всех ученых, кроме индийских, после Птолемея афелий смещается и приводит эти данные. А единственные отличные от всех остальных данные, которые он приводит, это полученные исламскими астрономами в Багдадском квартале Шамассия, где и так ясно, что в измерениях была какая то ошибка (наверное вытекающая из теории прецессии Сабита ибн Курры), т.к. там получилось AlfaP=61,5 градуса, что даже меньше чем у Птолемея.
И уж совсем не понятно, почему он не приводит данных из Зиджа Аль Хорезми, где у него AlfaP=77,92 градусов. И это при том, что его Зиджу он посвятил три огромные работы, где в основном защищает Аль Хорезми от нападок других астрономов и в то же время мы находим в Каноне Масуда данные вообще неизвестных астрономов (так и написано - автор данных не известен). Правда, в комментариях к Зиджу [10] делается предположение, что возможно это значение Аль Хорезми заимствовал у индийских астрономов, идеями которых он очень увлекался, но это никак не меняет сути дела, т.к. тогда получается, что и у индийских астрономов афелий смещался (хотя в таблицах Handy он действительно принят как у Птолемея). Здесь же стоит заметить, что полученное нами по таблицам AlKhwarizmi значение AlfaP=83,293 градуса (см. табл. 1) является результатом того, что или мы пользовались усовершенствованным вариантом таблиц AlKhwarizmi, или таблицы были составлены им после написания Зиджа, но и это в любом случае, свидетельствует о том, что у него афелий тоже смещается.
В то же время Аль Бируни пишет, что данные о началах и серединах времен года, полученные в течение 200 лет до него, близки к данным Птолемея и не противоречат друг другу. И он считает, что следствием этого является то, что «избыток /расстояние/ между центрами над двумя минутами малая величина, которая не остается постоянной из-за невозможности проверки наблюдений». А ведь нас как раз и интересует вопрос о величине эксцентриситета эксцентра, т.е. о расстоянии между центрами (с долготой афелия все более-менее ясно), но, как мы видим, Аль Бируни этот вопрос не только мало интересовал, но к тому же он считает, что, по имеющимся в то время данным, определить его точное значение не возможно. Тут же следует заметить, что всем параметрам орбиты Солнца обычно всеми древними астрономами посвящается целая глава, но эксцентриситету эксцентра никогда, т.к. эта малая величина при существующей тогда точности наблюдений не оказывала практически никакого влияния на координаты Солнца. Впервые отдельную главу (две страницы) я нашел в работе Риччиоли [7], где он даже приводит сводную таблицу значений эксцентриситета эксцентра и эллипса различных авторов, но в основном за 15 и 16 века, т.е. в то время, когда он работал.
Здесь надо также заметить и то, что, начиная примерно с Аль Баттани (см. рис. 11), исламские астрономы стали для нахождения параметров орбиты Солнца использовать не только описанную нами выше методику Птолемея, но и методику, немного отличающуюся от нее. Связано это с тем, что момент ЛС зафиксировать очень трудно, т.к. в это время высота Солнца изменяется очень медленно, по этому, астрономы стали фиксировать моменты середины весны и середины лета и по ним находить параметры орбиты Солнца. Примерно эту же методику использовали и астрономы XVII века (но по трем произвольным точкам), хотя многие уже использовали гелиоцентрическую модель Солнечной системы и планеты двигались у них по эллипсам.
К, сожалению, учитывая неоднозначность данных исламских ученых, приведенных в Каноне Масуда, я не вижу большого смысла в разборе возможных методологических ошибок этой методики, например, погрешности от рефракции или от параллакса при определение высоты Солнца в середине сезонов, хотя она будет очень существенной. Дело в том, что в то время по данным Аль Бируни расстояние от Земли до Солнца было 1233 диаметров Земли. Это примерно в два раза больше, чем у Птолемея, но сейчас это расстояние оценивается как 11719 диаметров Земли. Интересно заметить, что примерно эти же данные использовались и астрономами даже в начале XVII века (включая Тихо Браге), т.к. они считали, что параллакс Солнца был от 2,3 до 3 угловых минут. И только в начале XVII века Кеплером параллакс Солнца был уменьшен до 1 минуты, а в середине XVII века Джереми Хорокс до 15 угловых секунд и Стрит в своих таблицах использует уже это значение, но сейчас принято считать параллакс Солнца равным 8 угловым секундам. И, если кому-то это интересно, то он может провести такой анализ, ознакомившись с этой методикой в 6-ой книге Канона Масуда, а также в работе Стрита [11].
В этой же работе Стрит пишет, что только из-за не правильного значения параллакса Солнца, например, даты ВР и ОР Аль Баттани должны быть сдвинуты на 15 минут. Следовательно, продолжительности и весны и лета должны увеличиться на 15 минут. Если мы пересчитаем параметры Аль Баттани и Аль Бируни с этой поправкой, то получим значение эксцентриситета эксцентра отмеченное на рис3* и рис.4* синими квадратиками. Как видим, этой поправки не достаточно и сдвиг ВР и ОР должен быть примерно на 1 час. Следовательно, Стрит что то не так посчитал. К сожалению, я не могу сказать какова будет у Аль Баттани и Аль Бируни реальная ошибка не только от параллакса, но и от рефракции, т.к. не знаю точной методики определения ими координат Солнца при наблюдениях, а одна фраза Аль Бируни вообще приводит меня в замешательство. Определяя широту Солнца в Газне во время двух ОР он пишет «… я измерил высоту [Солнца] в меридиане с помощью квадранта, диаметр которого девять локтей … я нашел ее при помощи алидады несколько больше, чем 56 градусов и 43 угловых минуты, а при помощи отвеса – 56 градусов и 44 угловых минуты. Дополнение широты города [в этом случае] – 56 градусов и 25 угловых минут». Отсюда получается, что у него параллакс Солнца минус 19 угловых минут при переводе топоцентрических координат в геоцентрические, но такого не может быть. По этому, я вообще затрудняюсь сказать зачем он уменьшал широту Солнца даже если это у него как то связано с переводом горизонтальных координат в экваториальные.
Но, если предположить, что Стрит разобрался со всеми этими тонкостями, то возможно он при расчете сдвига даты на 15 минут не учел, что при методике исламских ученых ошибка в параллаксе Солнца будет двойной, т.к. она отразиться на дате середины сезонов весны и лета, и при этом рассчитанные начало весны и конец лета сдвинутся в два раза дальше, чем середины этих сезонов (при неизменной дате ЛС). К тому же, рассчитывая эту поправку, Стрит в любом случае определяет ее не верно, т.к. и сам использует не правильное значение параллакса Солнца (15 угловых секунд вместо 8), по этому сдвиг дат ВР и ОР должен быть как минимум в два раза больше и отклонение наблюдаемых значений от теоретических должно уменьшиться еще больше. И, если к этому прибавить поправку от рефракции, которая, как я писал выше, ссылаясь на работу [3], приведет к тому, что истинный момент ВР будет еще на 15 минут раньше момента, получившегося из измерений, а момент ОР еще на 15 минут позже, то в сумме мы получим почти 1 час. Таким образом, не только случайные, но и систематические ошибки в определение параметров орбиты Солнца у исламских ученых были и, следовательно, отклонение их данных от полученных нами расчетных данных вполне можно объяснить этими ошибками.
А теперь давайте посмотрим почему данные европейских астрономов примерно с 15-го века оказались завышенными. Причины здесь могут быть те же самые, т.к. значение параллакса Солнца у них были тоже завышены, но рефракцию примерно с 1600 года они уже стали учитывать (Тихо Браге и Кеплер). И здесь очень интересно отметить расхождение данных по эксцентриситету Стрита от всех остальных данных, т.к. они практически приблизились к нашим расчетным данным. А ведь, например, Кеплер и Стрит использовали для определения параметров орбиты одни и те же данные наблюдений и в основном это были данные Тихо Браге. Следовательно, расхождение в полученных ими значениях можно объяснить только тем, что Кеплер брал параллакс Солнца равный 1 угловой минуте, а Стрит 15 угловых секунд. И, если бы он взял правильное значение параллакса, т.е. 8 угловых секунд, то его данные приблизились бы еще ближе к нашим расчетным значениям.
Но это все теоретические предположения, базирующиеся на расчетах других астрономов, а при методике определения параметров орбиты Солнца по трем наблюдениям сделанным в разное время возможны отклонения параметров орбиты и в другую сторону. Эта же методика используется и сейчас, но она не дает ошибки, т.к. отсутствуют ошибки в самих данных наблюдений, а если в них имеется систематическая ошибка, то результат будет зависеть от выбора точек на орбите. Например, Стрит использовал наблюдения Тихо Браге в апреле, июле и сентябре, а если бы он использовал наблюдения в апреле, сентябре и январе, то должен был бы получить другую орбиту. А в том, что в параметрах орбиты Солнца, полученных астрономами в 16-17 веках, имеется систематическая ошибка, нет никаких сомнений. Ведь, если мы посмотрим на характер изменения эксцентриситета орбиты, полученный при обработке данных наблюдений за последние 200 лет, то становится ясно, что за 200 лет с 1800 до 1600 года он не мог так резко изменится. К тому же и такой разброс в данных Кеплера и Стрита говорит о том, что не все ладно с их методиками.
Но, чтобы окончательно убедится в том, что отклонения
параметров орбиты Солнца, полученных астрономами в 16-17 веках, объясняются
именно систематическими ошибками (не говоря уже о случайных) в учете параллакса
Солнца необходимо проанализировать саму методику проведения наблюдений и
методику учета поправок от рефракции и от параллакса (не считая аберрации). Но,
к сожалению, я и здесь не обладаю полной информацией о том, как все это
делалось в то время, по этому самостоятельно такой анализ провести не могу. А
хотелось бы для успокоения души обработать на программе Solsys
и данные Тихо Браге (при условие, что будет четко известно какие поправки в них
внесены). Ведь хотя принципиальная конструкция астрономических приборов,
которыми пользовался Тихо Браге, такая же, как и у приборов, описываемых
Птолемеем, но точности его измерений составляла 2…3![]() угловых минуты против нескольких десятков минут у его
предшественников. А по обширности его база наблюдательных данных далеко
превосходили все ранее сделанное до него.
угловых минуты против нескольких десятков минут у его
предшественников. А по обширности его база наблюдательных данных далеко
превосходили все ранее сделанное до него.
Но всех данных наблюдений Тихо Браге, приведенных к современному виду и собранных в одном месте я не видел. Можно конечно попытаться собрать эти данные из разных работ и выяснить как они были получены, но это уже, наверное, тема целого исследования, по тому, что, например, часть его наблюдений приводит в своей работе Стрит, но они почему то противоречат наблюдениям приведенным в работе Риччиоли [7] даже по высоте (хотя некоторые значения совпадают) и в таблицах 9-1 и 9-2 я привожу несколько наблюдений Тихо Браге из этих двух работ. А, если учесть, что почти все данные наблюдений Тихо Браге приведены в работах написанных на латыни, то для меня такая работа по приведению их к одному виду вообще не разрешима.
Таблица 9-1. Данные наблюдений за Солнцем Тихо Браге в марте и сентябре по данным Стрита.
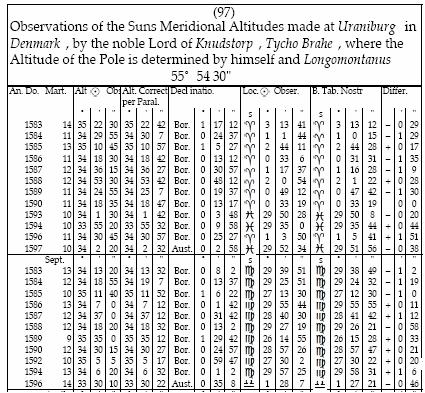
Таблица 9-2. Данные наблюдений за Солнцем Тихо Браге в марте и сентябре по данным Риччиоли.
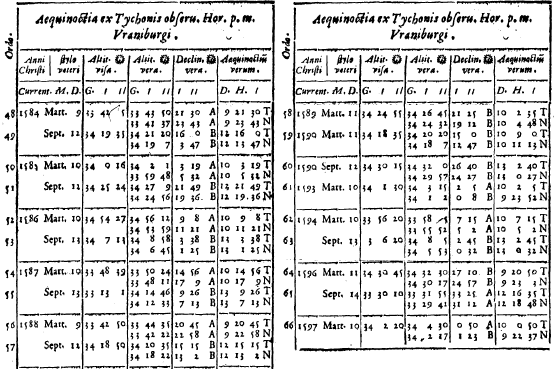
Но, как бы там в дальнейшем не решился вопрос с обработкой данных Тихо Браге и других астрономов того времени, например, Региомонтана, а основную для себя задачу я решил, т.е. я устранил противоречие в эксцентриситете орбиты Земли между данными древних астрономов и современных и теперь я для нахождения скорости гравитации могу найти истинные значения вековых смещений параметров орбиты Земли на интервале в 2000 лет, а не те, которые заложены в современные теории планет. А решить эту задачу надо было по тому, что от этого зависят не только истинные значения вековых смещений параметров орбиты Земли, но и, не смотря на малость величины эксцентриситета орбиты Земли, параметры орбит всех остальных планет. Ведь если мы обработаем современные данные наблюдений за Меркурием следующих обсерваторий Гринвичской, Парижской, USNO, CAPE и Оксфордской за период с 1770 по 1969 годы как с современными значениями вековых смещений параметров орбиты Земли, так и с теми, что я первоначально получил по данным древних астрономов (см. рис. 3 и 4), то мы получим совершенно разные значения вековых смещений параметров орбиты Меркурия (см. рис. 12 и 13).
Да, сейчас у меня на рис. 3* и 4* получились квадратичные зависимости изменения параметров орбиты Земли, отличающиеся от полученных первоначально на рис. 3 и 4, где у меня были линейные зависимости, но я обработал данные наблюдений с этими зависимостями, а не с квадратичными, чтобы более наглядно показать влияние характера изменения зависимости параметров орбиты Земли на параметры других планет. К тому же, полученные мною на рис. 3* и 4* квадратичные зависимости нуждаются в уточнение, по этому нет смысла использовать на этом этапе более сложные зависимости. А уточнить их надо по тому, что они после 2000 года получаются экстраполяцией продолжительности сезонов года, но у нас первичны не сезоны года, а параметры орбиты. По этому, надо после 2000 года получить параметры орбиты Земли на математической модели Солнечной системы, в которой должна использоваться скорость гравитации, полученная обработкой данных наблюдений до 2000 года. И возможно, что после 2000 года, например, эксцентриситет будет не увеличиваться по параболе, а экспоненциально приближаться к какому то значению, но в любом случае можно утверждать то, что в современных теориях (по крайней мере, до 2000 года) параметры орбиты Земли определены не верно.
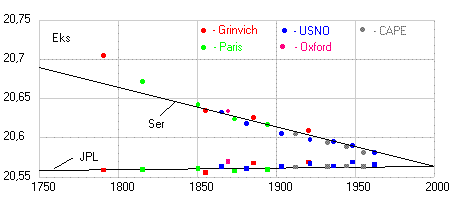
Рис 12. Изменение эксцентриситета
орбиты Меркурия в стандартной эпохе J2000 по данным оптических наблюдений пяти обсерваторий с
разными параметрами орбиты Земли (Ser – с моей предварительной (линейной) теорией – кружки, JPL – с теорией
JPL0
– квадратики). На рисунке значения увеличены в 1000 раз.
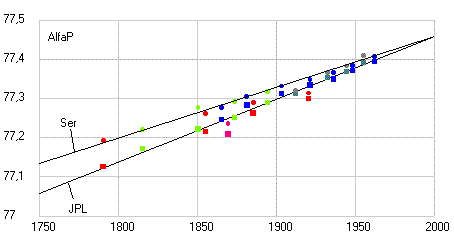
Рис 13. Изменение аргумента перигелия орбиты
Меркурия в стандартной эпохе J2000 по данным оптических наблюдений пяти обсерваторий с
разными параметрами орбиты Земли (Ser – с моей предварительной (линейной) теорией – кружки, JPL – с теорией
JPL0
– квадратики).
А из данных на рис. 12 и 13 получается, что,
задав нужные функции изменения параметров орбиты Земли, можно, обрабатывая одни
и те же данные оптических наблюдений за планетами, получить практически любые
нужные параметры орбит других планет. Надо, например, для Меркурия 43 угловых
секунды аномального смещения перигелия – пожалуйста. Надо для Меркурия 20
угловых секунд аномального смещения перигелия – пожалуйста. А у меня по
полученной мною предварительной теории Земли для аномального смещения перигелия
Меркурия получилось 65 угловых секунд (со знаком минус) в столетие. Для тех,
кто не в курсе, могу сообщить, что все физические теории тяготения, которые
создавались с конца 19-го века, т.е. после получения сначала Леверье, а потом Ньюкомом
аномального смещение перигелия Меркурия в 43 угловые секунды за 100 лет, и до
настоящего времени проверяются по критерию именно этого смещения. И в таблице
10 я привожу значения аномальных остатков полученных как самим Ньюкомом [13] при
обработке данных наблюдений, так и мною (с помощью программы Solsys) из его
теории New0 (с поправкой Холла в законе Ньютона, изложенной в [15]),
а также значения, которые дают различные физические теории тяготения (теория
Зееленгера чисто астрономическая).
Таблица 10. Аномальные остатки смещения перигелиев четырех внутренних планет
полученные из теории планет Ньюкома для фиксированной эклиптики J2000, которые
не объясняются теорией Ньютона, но объясняются другими теориями в дополнение к
смещению уже объясненному теорией Ньютона (в скобках указан источник, откуда
взяты данные).
|
Автор и источник |
Меркурий |
Венера |
Земля |
Марс |
|
Ньюком (Роузвер) |
41,2 |
-7,3 |
6,0 |
8,0 |
|
Ньюком (Юдин) |
40,9 |
10,2 |
15,4 |
0,8 |
|
Эйнштейн (Субботин) |
43,0 |
8,6 |
3,8 |
1,4 |
|
Гербер (Хайдаров) |
43,0 |
8,6 |
3,8 |
1,4 |
|
Ритц (Роузвер) |
41,0 |
8,0 |
3,4 |
- |
|
Мах (Зайцев) |
43,0 |
23,0 |
17,0 |
11,0 |
|
Зеелингер (Роузвер) |
41,3 |
7,3 |
4,2 |
6,3 |
Таким образом, все современные теории, базирующиеся, как на теории Ньютона (как с поправкой Холла, так и без нее, т.е. Ньюкома и Леверье), так и на общей теории относительности (DE405, INPOP06, ЕРМ2004), где кругом скорость распространения гравитации принимается равной бесконечности (кстати, вопреки постулатам самой теории относительности о том, что никакая скорость взаимодействия не может быть больше скорости света) являются по большому счету искусственными теориями. Почему же так получилось, что в этих теориях заложены не правильные значения вековых смещений параметров орбит планет, и в то же время полученные с их помощью данные всех устраивали. Объясняется это особенностью расчета координат планет по современным теориям. Дело в том, что в настоящее время с различными вариациями известны две методики определения параметров орбит планет по наблюдательным данным. Типичными результатами применения первой методики являются теория Птолемея и законы Кеплера, а второй аналитические теории планет Леверье и Ньюкома и полученные численными методами эфемериды JPL. А т.к. классификации этих методик я нигде не встречал, то, во-первых, мне придется дать им названия, допустим, кинематическая и динамическая или физическая, т.е. с использованием физических законов, а, во-вторых, мне же придется и указать на их отличия.
До тех пор пока не были сформулированы три механических закона Ньютона и закон всемирного тяготения физических методик быть не могло. И по этому даже Кеплер, открывший в 1609 году два своих первых закона и в том числе о движение планет по эллипсам использовал кинематическую методику. При кинематической методике, например, Птолемей, аппроксимируя данные наблюдений, находил непосредственно параметры орбит в геоцентрической системе координат (радиусы эпициклов и деферентов), предполагая равномерное вращение различных сфер с этими параметрами, а современные астрономы поступают иначе. Они по данным наблюдений находят оптимальные параметры их математических моделей, построенных с использованием физических теорий, где используется та или иная модификация закона притяжения Ньютона. При этом, в кинематической методике угловая скорость планет рассчитывалась по нескольким реперным точкам, т.е. по 2-м или 3-м наблюдениям планет сделанным на очень большом интервале времени. Например, в начале нашей эры и в 17-м веке и получалось, что положения планет по углу поворота они удовлетворительно описывали на всем этом интервале при использование в качестве аргумента солнечного времени UT. А при современной методике скорость определяется исходя из физических законов и принятой системы масс планет, где главную роль, конечно же играет принятое значение массы Солнца.
При этом параметры математической модели (массы планет) подбираются так, чтобы удовлетворительно аппроксимировать данные наблюдений за 100...200 лет, а далее идет чистый расчет по полученной математической модели. При этом, т.к. параметры орбит планет за 200 лет изменяются не значительно, то практически любой физический закон, положенный в основу математической модели, позволяет удовлетворительно аппроксимировать данные наблюдений. Естественно, при учете периодических возмущений от других планет, т.к. их влияние на координаты планеты будет во много раз больше влияния от изменения параметров орбит. Но вот при интерпретации расчетных данных современных теорий на большие промежутки времени возникают реальные проблемы. И дело здесь не в том, что эллипсы орбит со временем немного смещаются в пространстве и, следовательно, со временем немного изменяются параметры орбит, например, аргумент перигелия или угол восхождения. Такое смещение обеспечивается причинно-следственной связью физических моделей и, следовательно, при обработке данных наблюдений мы при этом априори принимаем закон изменения вековых смещений параметров орбит, вытекающий из этих физических теорий, но это конкретное смещение, как я писал, не очень сильно влияет на расчетные положения планет и к тому же основное смещение параметров орбит дает и закон Ньютона. Основная проблема возникающая в современных методиках получения теорий планет это использование в них математического, т.е. равномерно текущего, времени (его еще называют эфемеридным временем ET), которое отличается от реального солнечного времени наблюдений UT. По этому, для расчета координат планет по современным теориям приходится опытным путем подбирать эфемеридную поправку ET-UT для уточнения времени наблюдения для этих теорий и всегда можно ее подобрать так, что для какого-то конкретного наблюдения мы получим нужный нам результат.
Суть же моей методики, вернее несколько модифицированной кинематической
методики древних астрономов, которую я применял для обработки данных оптических
наблюдений за последние 200 лет и данных, полученных из таблиц древних
астрономов, состоит в том, что, так же как, например, у Кеплера заранее
задается, что планеты движутся по эллиптическим орбитам, параметры которых не
меняются на ограниченном промежутке времени (кроме средней аномалии), и их
координаты в разные моменты времени сравниваются с данными наблюдений. При этом
у меня в качестве аргумента кругом используется естественное солнечное время UT. Вот только
в отличие от Кеплера при подборе оптимальных значений пяти параметров
эллиптической орбиты планеты я применяю методы многофакторного планирования,
которые позволяют автоматизировать этот процесс, а не искать их оптимальное
соотношение простым перебором всех возможных вариантов. Расписывать подробно теорию
многофакторного планирования я не буду. Кому интересно ознакомится с этим очень
мощным статистическим методом обработки данных можете посмотреть это скачав
программу Solsys или в моей
книге [16], а можно и в моих темах на форумах, например, здесь http://www.astronomy.ru/forum/index.php/topic,31389.msg675343.html#msg675343
.
И, если можно получить вполне удовлетворительные данные, например, по времени затмений древних наблюдений с помощью современных теорий (с учетом эфемеридной поправки ET-UT), то и по современным затмениям можно точно также получить удовлетворительные данные с помощью теорий древних астрономов (чаще всего опять же с учетом эфемеридной поправки ET-UT). При этом, замечу, что создаваемая мною кинематическая теория планет не нуждается в эфемеридной поправке. И если мы сравним, например, время солнечных затмений 136 года до н.э. и 2006 года н.э., рассчитанное по современным теориям и по теориям древних астрономов, то мы не увидим больших отличий в полученных данных. При этом лучше сравнивать солнечные затмения, т.к. они видны только в узкой полосе и в точно заданное время в отличие от лунных затмений, которые видны с очень многих точек на Земле и древним астрономам приходилось очень субъективно определять фазу затмения, которую они наблюдают в своем пункте. При этом, как будет показано далее, точность расчета затмения определяется не столько точностью параметров орбит Земли и Луны и даже не тем геоцентрическая это теория или гелиоцентрическая или движутся Земля и Луна по эллипсам или по эксцентрам (эпициклам), а периодом времени, за который использовались данные наблюдений для создания теорий, продолжительность которого оказывает влияние на определение средней угловой скорости планет и Луны.
Но, обо всем об этом позже, а сейчас давайте рассмотрим конкретное солнечное затмение, которое наблюдалось в Вавилоне 15 апреля в 136 году до н.э. по Григорианскому (Юлианскому) календарю. Это одно из немногих затмений, которое описано очень точно и по этому здесь нельзя расхождения наблюдаемых данных и расчетных объяснить не точностью сведений. Описывается оно так. Тень двигалась с Юго-Запада на Северо-Восток. Началось затмение через 96 минут после восхода Солнца (это будет примерно 7 часов 10 минут местного времени LTet). Затмение стало полным через 72 минуты и от начала затмения до конца прошло 140 минут. Результаты расчетов поместим в таблицу 11, но местное время LT восхода и фаз затмения будем указывать не по всемирному солнечному времени LTut, а с учетом эфемеридной поправки ET2-UT , т.е. LTet. При этом, к уже устоявшемуся понятию эфемеридной поправки для корректировки угла поворота планет вокруг Солнца и Луны вокруг Земли ET1-UT введем еще одну эфемеридную поправку для корректировки угла поворота Земли вокруг своей оси ET2-UT (в таблице они обозначены как ET1 и ET2). А теперь сравним данные наблюдений с расчетными данными, используя программу Solsys7 (в 6-ой версии, которая выложена у меня на сайте сейчас, этой формы нет).
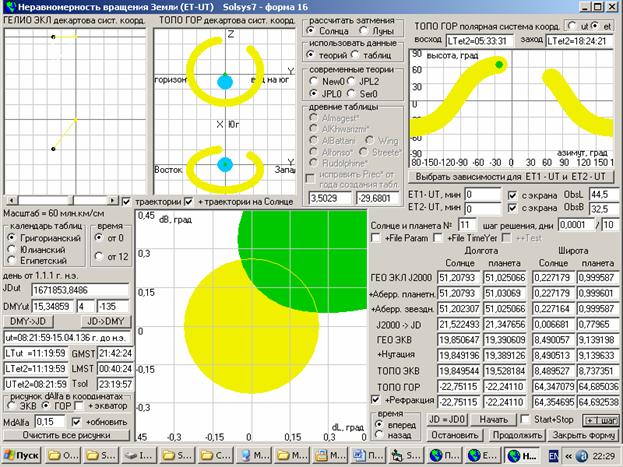
Рис. 14 Скриншот формы 16 программы Solsys7 с расчетом солнечного затмения 15 апреля 136 г. до н.э. по теории JPL0 без эфемеридных поправок (максимальная фаза затмения).
В программе Solsys для современных теорий, где рассчитываются геометрические координаты планет, в эти данные вносится погрешность от звездной и планетной аберрации, затем эклиптические гелиоцентрические координаты переводятся в экваториальные геоцентрические и в них вносится погрешность от нутации, а для теорий JPL еще и переводятся координаты из стандартной эпохи J2000 в эпоху даты. Далее координаты переводятся в экваториальные топоцентрические, а потом в горизонтальные. А вот в таблицах древних астрономов приводятся видимые геоцентрические эклиптические координаты, по этому их надо только перевести в экваториальные топоцентрические, а потом в горизонтальные, чтобы сравнить расчетные данные с данными наблюдений. Но кроме этого в теориях и в докеплеровских таблицах надо еще учесть рефракцию (про таблицы Prutenic ничего определенного сказать не могу, т.к. созданы они в 1551 году, а атмосферную рефракцию первым начал учитывать Вольтер (1430-1504) и теоретически Рейнгольд мог ее учесть, но точных данных об этом у меня нет).
Время начала и конца затмения определяется в программе визуально по анимации отражающей движение Луны относительно Солнца, координаты которого на анимации остаются неизменными. Визуальный способ, конечно же, вносит некоторую ошибку в точность определения этих моментов, но для моих исследований меня эта точность вполне устраивает. При этом, анимацию можно воспроизвести, как в горизонтальных координатах, так и в экваториальных. Лучше, конечно же, воспроизводить в горизонтальных координатах, т.к. в описаниях затмений говорится откуда и куда двигалась тень так как ее наблюдали, и по этому в горизонтальных координатах я и определял время и фазу затмений в таблицах 11 и 12. При этом фаза затмений определялась мною не по площади перекрытия дисков Луны и Солнца, а по перекрытию их диаметров и в тех случаях, когда не получалось полного затмения, я указывал время максимальной фазы затмения. Для таблиц до Кеплера, когда астрономы еще не учитывали атмосферную рефракцию, хотя о ней писал еще Птолемей, я при расчетах горизонтальных координат не делаю поправку на рефракцию.
Здесь надо заметить, что моя программа дает еще небольшую погрешность при расчете положения объектов относительно центра Солнца, обусловленную тем, что как горизонтальные, так и экваториальные координаты являются конической системой координат. Вследствие этого истинное расстояние между двумя точками по долготе или азимуту с увеличением склонения или высоты получаются все меньше и меньше (аналогично уменьшению расстояния между двумя меридианами при приближение к северному полюсу Земли). Точный учет этого обстоятельства при воспроизведении анимации затмений требует очень существенного усложнения кода программы, но полученная при этом поправка будет микроскопической по сравнению с приближенным решением, примененным мною для учета этого явления. А суть приближенного решения сводится к тому, что я воспроизвожу при анимации положение объектов относительно Солнца (по разности координат их центров) в прямоугольной системе координат, но истинное расстояние по долготе или азимуту вычисляю с учетом склонения или высоты центра Солнца. А т.к. воспроизводится очень маленький участок сферы с размерами по координатам менее 1 градуса (видимый диаметр Солнца 0,52 градуса), то можно считать этот участок примерно квадратным.
И две маленьких ремарки к данным таблицы 11. По Альфонсовым таблицам дата Вавилонского затмения получается не 15-го апреля, а 14-го, но это не ошибка самих таблиц. Это ошибка Ларса Гисленда, который переложил эти таблицы в формат таблиц Excel, а при переложение допустил ошибку в формуле определения юлианской даты в один день для дат до нашей эры, хотя в его таблицах Стрита в этой же формуле эта ошибка уже исправлена. Теория JPL2 (эфемериды DE405) были созданы для использования с 1600 по 2200 годы, а ее упрощенный вариант JPL0 (для использования с 1800 по 2050 годы http://ssd.jpl.nasa.gov/txt/p_elem_t1.txt ), а для промежутка с -3000 по 3000 годы была создана немного отличающаяся от нее теория JPL2 (эфемериды DE406 и для Луны отдельно LE406) и их упрощенный вариант JPL0 http://ssd.jpl.nasa.gov/txt/p_elem_t2.txt , но различия в них настолько малы, что я не стал перегружать свою программу Solsys7 еще и вариантом работы с этими эфемеридами, а использовал упрощенный вариант эфемерид DE405 (JPL0) и для расчета затмения для 136 года до н.э. Например, эксцентриситет орбиты Земли по двум упрощенным вариантам этих теорий получается 0,01765 и 0,01751, но никак не 0,0204, как это должно быть. Кроме того, JPL не приводит данных упрощенного варианта по Луне, по этому я использую для нее, также как и для теории New0 упрощенную теорию Брауна.
Таблица 11. Параметры солнечного затмения 15.04.-135 года наблюдавшегося в Вавилоне (долгота 44,5 в.д., широта 32,5 с.ш.) и полученные по данным эфемерид таблиц древних астрономов и современных теорий. Для теории Ньюкома эфемеридные поправки рассчитаны только по формуле Далмау, а для таблиц по формуле Далмау, но отсчет идет не от 1800 года, а от года создания таблиц. Время дано местное (Вавилон) солнечное. Звездочкой отмечены данные с исправленной прецессией.
|
Название таблиц, теорий
|
Фаза в %
|
Восход |
Начало |
Начало полного |
Конец |
Итого |
|
Наблюдаемые данные |
100 |
05:34 |
07:10 |
08:22 |
09:30 |
02:20 |
|
JPL0 ET1=0 ET2=0 |
30 |
05:33 |
10:37 |
11:20 |
12:23 |
01:46 |
|
Джонс ET1=182,5 ET2=0 |
99 |
05:34 |
06:41 |
07:41 |
08:46 |
02:05 |
|
Джонс ET1=0 ET2= -182,5 |
99 |
05:34 |
06:41 |
07:41 |
08:46 |
02:05 |
|
Далмау ET1=196,5 ET2=0 |
100 |
05:34 |
06:27 |
07:24 |
08:29 |
02:02 |
|
Далмау ET1=0 ET2= -196,5 |
100 |
05:34 |
06:27 |
07:24 |
08:29 |
02:02 |
|
JPL0 ET1=156,0 ET2=0 |
90 |
05:34 |
07:10 |
08:09 |
09:18 |
02:08 |
|
New0 ET1=0 ET2=0 |
30 |
05:33 |
10:36 |
11:21 |
12:21 |
01:45 |
|
New0 ET1=196,5 ET2=0 |
100 |
05:34 |
06:26 |
07:23 |
08:28 |
02:02 |
|
Almagest ET1=0 ET2=0 |
96 |
05:37 |
07:08 |
08:13 |
09:23 |
02:15 |
|
Almagest ET1=3,9 ET2=0 |
96 |
05:37 |
07:03 |
08:08 |
09:17 |
02:14 |
|
Almagest* ET1=0 ET2=0 |
99 |
05:34 |
07:08 |
08:14 |
09:24 |
02:16 |
|
AlKhwarizmi ET1=0 ET2=0 |
20 |
06:39 |
14:17 |
15:20 |
16:01 |
01:44 |
|
AlKhwarizmi ET1=45,9 ET2=0 |
35 |
06:39 |
12:50 |
14:07 |
15:02 |
02:12 |
|
AlKhwarizmi* ET1=0 ET2=0 |
10 |
05:42 |
15:19 |
15:51 |
16:24 |
01:05 |
|
AlBattany ET1=0 ET2=0 |
86 |
05:32 |
06:27 |
07:27 |
08:34 |
02:07 |
|
AlBattany ET1=56,2 ET2=0 |
76 |
05:32 |
05:32 |
06:27 |
07:26 |
01:54 |
|
Alfonso ET1=0 ET2=0 |
77 |
05:42 |
07:53 |
08:57 |
10:10 |
02:17 |
|
Alfonso ET1=101,0 ET2=0 |
99 |
05:43 |
06:06 |
07:04 |
08:08 |
02:02 |
|
Alfonso* ET1=0 ET2=0 |
77 |
05:36 |
07:55 |
09:02 |
10:15 |
02:20 |
|
Rudolphine ET1=0 ET2=0 |
92 |
05:34 |
06:47 |
07:47 |
08:52 |
02:05 |
|
Rudolphine ET1=158,0 ET2=0 |
70 |
05:35 |
04:19 |
05:07 |
05:57 |
01:44 |
|
Rudolphine* ET1=0 ET2=0 |
92 |
05:35 |
06:46 |
07:46 |
08:51 |
02:05 |
|
Streete ET1=0 ET2=0 |
95 |
05:34 |
07:23 |
08:27 |
09:37 |
02:13 |
|
Streete ET1=161,6 ET2=0 |
67 |
05:35 |
04:47 |
05:36 |
06:26 |
01:39 |
|
Streete* ET1=0 ET2=0 |
97 |
05:32 |
07:24 |
08:28 |
09:39 |
02:15 |
|
Wing ET1=0 ET2=0 |
92 |
05:34 |
06:51 |
07:51 |
08:58 |
02:07 |
|
Wing ET1=165,4 ET2=0 |
70 |
05:35 |
04:16 |
05:03 |
05:54 |
01:38 |
Как мы видим, применение современных теорий, полученных с использованием динамической методики, для древних затмений дает очень плачевные результаты. Сейчас эти ошибки объясняются тем, что Земля замедляет скорость вращения вокруг своей оси и по этому по современным теориям для заданного солнечного времени наблюдения (UT) получается, что Земля откручивается назад (для древних наблюдений) на угол меньше, чем надо. Следовательно, надо при заданной в теории постоянной угловой скорости вращения Земли отвернуть ее назад еще ну угол, который она сделает за время ET2 - UT, где ET это эфемеридное (равномерно текущее) время, которое используется или при аналитическом моделировании (New0) или при численном, т.е. на компьютере (JPL2). Ведь один оборот вокруг своей оси Земля делает за 24 солнечных часа (UT) и сейчас и делала миллиард лет назад, но вот продолжительность этих часов, если измерять продолжительность солнечного часа атомными часами, будет различной. И согласно палеонтологическим исследованиям (по отложениям ракушек) миллиард лет назад Земля делала один оборот за 18 часов (при условии, что не меняется период обращения Земли вокруг Солнца).
Таким образом, и планеты вокруг Солнца и Луна вокруг Земли за один солнечный час (при их неизменной по атомным часам угловой скорости орбиты) повернутся в разное историческое время на разные углы, т.к. продолжительность солнечного часа будет разной. Сама продолжительность суток изменяется на очень маленькую величину (примерно на 1,5 – 2,0 миллисекунды в столетие и, например, за три тысячи лет изменение продолжительности суток составит примерно 0,05 секунды), но разница между прошедшим солнечным временем и эфемеридным за несколько тысячелетий составит уже часы. А, т.к. при расчете эфемерид (координат) планет по современным теориям у нас как раз и используется время, прошедшее от какой то стандартной эпохи, для которой зафиксировано положение планет и их угловая скорость, до даты, для которой мы рассчитываем координаты, то нам как раз и надо знать какая разница между эфемеридным и солнечным временем набежала за этот промежуток времени по солнечным (календарным) часам. По этому, при расчете по современным физическим теориям нам надо обязательно учесть набежавшую разницу во времени, которая называется эфемеридной поправкой ET-UT.
Вот только рассчитывать теоретически эту поправку астрономы пока не умеют и по этому просто подбирают нужное значение эфемеридной поправки, чтобы согласовать время наступления солнечных или лунных затмений, рассчитанных по современным теориям, со временем, зафиксированным в древних хрониках, а для будущего приходится только гадать, как эта поправка будет изменяться. Но, как видно по данным на рис. 15, аппроксимировать нужное для современных теорий значение эфемеридной поправки можно очень большим количеством различных выражений. Сейчас наиболее широко известны эмпирические формулы для расчета эфемеридной поправки (для прошлого) Джонса (была официально одобрена Международным астрономическим союзом в 1952 г. и применялась в расчетах до 1986 г.) и Далмау (1997 г.), а также табличные данные Стефенсона (1997 г.). В приведенных ниже формулах ET-UT получается в секундах при времени T (в столетиях), отсчитываемом от начала 1900 г. у Джонса и от начала 1800 г. у Далмау. Обе зависимости имеют вид параболы, вершина которой находится около 1814 года, что, в общем-то, странно, т.к. согласно определению скорость течения эфемеридного и солнечного времени принимается равной в 1900 году и, следовательно, расхождения между ними должны идти как две ветви параболы от 1900 года. Но, может быть, такая странность объясняется скачкообразным изменением скорости вращения Земли именно в 1814 году, например, падением метеорита типа Тунгусского, и тогда зависимость Далмау является более объективной для прошлого.
ET-UT = 24.349 + 72.318*T + 29.950*T2 (Джонс)
ET-UT= 31.5*T2
(Далмау)
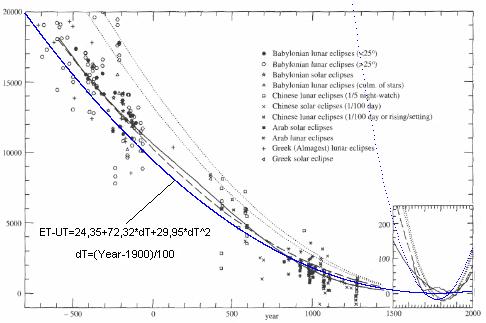
Рис. 15 Величина эфемеридной поправки необходимая для современных теорий для согласования экспериментальных данных солнечных и лунных затмений начиная с 700 г. до н.э. (взято из работы Стефенсона). Рисунок дополнен мною аппроксимацией этих данных зависимостью Джонса.
Но астрономы при расчете координат планет и Луны при учете эфемеридной поправки для прошлого не доворачивают Землю назад на время ET-UT, а наоборот доворачивают планеты и Луну вперед. Что в принципе из-за Луны даст тот же самый эффект при рассмотрении солнечных и лунных затмений (смотрите данные JPL0), т.к. при той же самой поправке для поворота планет вокруг Солнца и Луны вокруг Земли ET1-UT и для поворота Земли вокруг своей оси ET2-UT получаются одни и те же данные. Я же предпочитаю при расчетах использовать поправку ET2-UT, которая влияет на расчетные значения местного солнечного (LTet) и звездного (LMSTet) времени, которые я использую для преобразований геоцентрических координат в топоцентрические и экваториальных координат в горизонтальные, а местное солнечное календарное время LTut я оставляю без изменений. Дело в том, что один и тот же эффект от такой замены поворота Земли вокруг своей оси на поворот планет будет только при одном условие, когда угловые скорости обращения планет вокруг Солнца и Луны вокруг Земли будут оставаться неизменными. А вот это условие не является доказанным и судя по тому, что, например, Луна удаляется от Земли на 3,8 сантиметра в год мы должны иметь (согласно закону сохранения энергии) замедление ее вращения. Хотя сейчас кругом пишут, что Луна ускоряет свое вращение за счет крутящего момента, который создают приливы.
Но, если по Луне есть хоть какие-то данные, то вот по планетам этот вопрос совершенно не изучен. И, если они изменяют свою скорость обращения вокруг Солнца (в равномерно текущем времени), то необходимо учитывать эту поправку отдельно от поправки для угла поворота Земли вокруг своей оси. По этому, я и разделил поправку ET-UT на две ET1-UT и ET2-UT, которые должны рассчитываться по разным формулам, но как получить эти формулы я пока ума не приложу. Дело в том, что по данным затмений их не получить, т.к. они взаимосвязаны и эффект от поворота Луны вокруг Земли и Земли вокруг своей оси получается один и тот же. Возможно, что-то удастся получить по данным транзита планет по диску Солнца, но, я не встречал таких данных наблюдений примерно до 1600 года (может быть без телескопа нельзя и увидеть транзит Меркурия и Венеры, хотя Авиценна утверждал, что он в XI веке наблюдал транзит Венеры, а Ибн Баджах говорил о том, что он в XII веке наблюдал и транзит Венеры и транзит Меркурия). Так, что мое разделение эфемеридной поправки на две остается пока чисто теоретическим вопросом. По этому в таблицах 11, 12 и 13 я кругом (кроме расчета в таблице 11 по JPL0 и в таблице 12 по Almagest) даю расчет только при использование поправки ET1-UT, т.е. так как это и принято у астрономов сейчас (для таблиц используется поправка Далмау не от 1800 года, а от года создания таблиц).
А вот для таблиц древних астрономов (при расчете в прошлое)
вопроса по эфемеридным поправкам не существует в принципе, т.к. эти теории
создавались с использованием кинематической методики, а не динамической (с
использованием законов физики), как современные теории. При создании
современных теорий, чтобы начать вычисления, надо задать начальные условия
(координаты и скорости) на конкретную дату (обычно берется дата создания
теорий), а древние астрономы задавали две пары координат на две конкретных даты,
а скорость вычисляли среднюю за весь период имеющихся у них данных наблюдений,
т.е. между этими датами. Обычно они использовали данные от начала нашей эры и
до даты создания таблиц, по этому при расчете координат на начало нашей эры они
и получали координаты, которые реально наблюдались в это время. И, как видно из
таблицы 11, эфемеридная поправка почти у всех только ухудшает результат. А вот
при расчете координат для будущего и для таблиц древних астрономов надо
использовать какую-то эфемеридную поправку, но как ее рассчитывать, если
угловая скорость бралась средней за период, за который имелись данные
наблюдений, не понятно. Здесь только с таблицами Птолемея более менее ясно,
т.к. у него в историческом плане данные наблюдений были за очень не большой
промежуток времени и ошибка в определение времени T для
формулы Далмау будет не большой. Посмотрим как повлияет эфемеридная поправка на
данные таблиц древних астрономов для современного затмения.
Возьмем, например, фотоотчет о солнечном затмение в п. Кировский Астраханской области http://fomalhautpskov.narod.ru/bestobservation/sun_eclipse_29_03_06.html , в котором хоть и отсутствует время окончания затмения, но это именно данные наблюдений, а не расчетные данные, которые мы всегда и в любом виде можем найти на сайте НАСА. А кроме того, по приведенным в отчете данным, легко найти и время окончания затмения. Автор указывает, что начало затмения было в 14:12:37, а начало фазы полного затмения было в 15:22:57 и, следовательно, прошло 1:10:20. Если предположить, что и от окончания фазы полного затмения (15:25:49) прошло 1:10:20, то получится, что окончание затмения было в 16:36:09, а общая продолжительность была 2 часа 23 минуты и 32 секунды. Эти данные хорошо согласуются и с отчетами нескольких экспедиций наблюдавших затмение на горе Эльбрус, например, здесь http://www.astrogalaxy.ru/download/foto292006.zip , согласно которым начало и конец затмения были примерно в 14:03 и 16:27 (время отличается из-за долготы точек наблюдения), т.е. продолжительность составила 2 часа 24 минуты.
Таблица 12. Параметры солнечного затмения 29.03.2006 года наблюдавшегося в п. Кировский Астраханской области (долгота 48,153 в.д., широта 45,874 с.ш.) и полученные по данным эфемерид таблиц древних астрономов и современных теорий. Для теорий JPL2, JPL0 и New0 эфемеридные поправки рассчитаны по кусочной аппроксимации экспериментальных данных последнего времени, а для таблиц по формуле Далмау, но отсчет идет не от 1800 года, а от года создания таблиц (значение ET1=100 минут для таблиц Птолемея взято произвольно). Время дано всемирное (Гринвич) солнечное. Звездочкой отмечены данные с исправленной прецессией.
|
Название таблиц, теорий
|
Фаза в %
|
Восход |
Начало |
Начало полного |
Конец |
Итого |
|
Наблюдаемые данные |
100 |
05:47 |
10:13 |
11:23 |
12:36 |
02:23 |
|
JPL2 ET1=0 ET2=0 |
100 |
05:47 |
10:13 |
11:25 |
12:35 |
02:22 |
|
JPL2 ET1=1,3 ET2=0 |
100 |
05:47 |
10:12 |
11:23 |
12:33 |
02:21 |
|
JPL0 ET1=0 ET2=0 |
100 |
05:47 |
10:11 |
11:22 |
12:31 |
02:20 |
|
JPL0 ET1=1,3 ET2=0 |
100 |
05:47 |
10:09 |
11:20 |
12:29 |
02:20 |
|
New0 ET1=0 ET2=0 |
100 |
05:47 |
10:11 |
11:22 |
12:31 |
02:20 |
|
New0 ET1=1,3 ET2=0 |
100 |
05:47 |
10:09 |
11:20 |
12:29 |
02:20 |
|
Almagest ET1=0 ET2=0 |
58 |
05:32 |
12:29 |
13:23 |
14:20 |
01:51 |
|
Almagest ET1=183,0 ET2=0 |
94 |
05:32 |
08:28 |
09:44 |
10:58 |
02:30 |
|
Almagest* ET1=0 ET2=0 |
60 |
05:47 |
12:24 |
13:21 |
14:20 |
01:56 |
|
Almagest* ET1=183,0 ET2=0 |
100 |
05:47 |
08:14 |
09:30 |
10:47 |
02:33 |
|
Almagest* ET1=0 ET2= -183,0 |
100 |
05:47 |
08:14 |
09:30 |
10:47 |
02:33 |
|
Almagest* ET1=100,0 ET2=0 |
75 |
05:47 |
10:11 |
11:21 |
12:29 |
02:18 |
|
AlKhwarizmi ET1=0 ET2=0 |
95 |
05:22 |
09:17 |
10:33 |
11:46 |
02:29 |
|
AlKhwarizmi ET1=76,4 ET2=0 |
75 |
05:22 |
07:36 |
08:41 |
10:11 |
02:35 |
|
AlKhwarizmi* ET1=0 ET2=0 |
100 |
05:46 |
08:57 |
10:16 |
11:34 |
02:37 |
|
AlKhwarizmi* ET1=76,4 ET2=0 |
70 |
05:46 |
07:18 |
08:23 |
09:52 |
02:34 |
|
AlBattany ET1=0 ET2=0 |
80 |
05:54 |
11:37 |
12:42 |
13:50 |
02:13 |
|
AlBattany ET1=64,2 ET2=0 |
90 |
05:54 |
10:11 |
11:24 |
12:36 |
02:25 |
|
Alfonso ET1=0 ET2=0 |
100 |
05:50 |
10:08 |
11:22 |
12:33 |
02:25 |
|
Alfonso ET1=29,9 ET2=0 |
90 |
05:50 |
09:28 |
10:41 |
11:57 |
02:29 |
|
Alfonso* ET1=0 ET2=0 |
98 |
05:59 |
10:00 |
11:16 |
12:29 |
02:29 |
|
Alfonso* ET1=29,9 ET2=0 |
88 |
05:59 |
09:21 |
10:33 |
11:52 |
02:31 |
|
Rudolphine ET1=0 ET2=0 |
95 |
05:47 |
10:31 |
11:40 |
12:48 |
02:17 |
|
Rudolphine ET1=8,7 ET2=0 |
98 |
05:47 |
10:20 |
11:30 |
12:37 |
02:17 |
|
Rudolphine* ET1=0 ET2=0 |
95 |
05:47 |
10:31 |
11:40 |
12:48 |
02:17 |
|
Rudolphine* ET1=8,7 ET2=0 |
98 |
05:47 |
10:20 |
11:30 |
12:37 |
02:17 |
|
Streete ET1=0 ET2=0 |
96 |
05:47 |
10:26 |
11:36 |
12:45 |
02:19 |
|
Streete ET1=7,8 ET2=0 |
100 |
05:47 |
10:16 |
10:27 |
12:35 |
02:19 |
|
Streete* ET1=0 ET2=0 |
96 |
05:47 |
10:26 |
11:36 |
12:45 |
02:19 |
|
Streete* ET1=7,8 ET2=0 |
100 |
05:47 |
10:16 |
11:27 |
12:35 |
02:19 |
|
Wing ET1=0 ET2=0 |
96 |
05:47 |
10:39 |
11:48 |
12:56 |
02:17 |
|
Wing ET1=7,0 ET2=0 |
98 |
05:47 |
10:29 |
11:39 |
12:47 |
02:18 |
Что касается современных теорий, то у них результаты получаются отличные, что, собственно говоря, и должно быть. При этом теории JPL0 и New0 дают практически один и тот же результат, т.к. для обеих теорий планет я использую одну и ту же теорию Луны (Брауна), а именно Луна оказывает самое заметное влияние на параметры затмения. А вот таблицы древних астрономов показывают очень разные результаты. Более-менее современные таблицы 17 века Кеплера, Стрита и Винга тоже показывают хорошие результаты, что в принципе тоже было предсказуемо, т.к. эфемеридная поправка здесь меньше 10 минут и не оказывает большого влияния, а вот у остальных таблиц при значительной эфемеридной поправке результаты очень противоречивые. Таблицам Птолемея, АльХорезми и АльБаттани поправка пошла на пользу, а в Альфонсовых таблицах наоборот немного ухудшила результат. Но, не смотря на это, просматривается явная потребность во введение своей эфемеридной поправки и для таблиц древних астрономов. Вот только как ее корректно определять для этих таблиц, когда угловая скорость планет бралась не на дату создания таблиц, а средняя за период, за который имелись данные наблюдений, как я уже писал, я не знаю (да и за какой период использовались авторами таблиц данные известно не всегда).
Но расчетные данные таблиц древних астрономов (при расчете в будущее) можно улучшить не только за счет эфемеридной поправки, но и подкорректировав значение прецессии заложенное в них. Это надо сделать по тому, что из-за недостаточного количества экспериментальных данных в таблицах древних астрономов (кроме таблиц 17 века) у них получается очень плохой прогноз прецессии для будущего (кстати, напомню, что современные астрономы до сих пор не могут прогнозировать эфемеридную поправку). И для таблиц, где прецессия рассчитывается отдельно, я в программе Solsys7 сделал опцию исправления прецессии от даты создания таблиц, а в таблицах Птолемея прецессия не вычисляется отдельно, но ее можно тоже исправить, т.к. мне известно его значение прецессии и его значение долготы первой звезды в созвездие Овна на дату составления его таблиц. По всем таблицам, где прецессия рассчитывается отдельно, а не является составной частью других расчетов, например, долготы Солнца, я построил графики ее изменения (см. рис. 16). А по остальным таблицам я определил дату летнего солнцестояния, т.е. день, когда геоцентрическая эклиптическая долгота Солнца в таблицах получается ровной 90 градусов, и тоже построил графики по этим зависимостям (см. рис. 17).
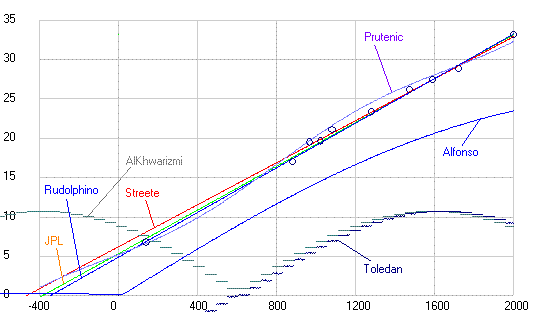
Рис. 16 Прецессия по данным таблиц древних астрономов и по современным данным (JPL) или непосредственно от первой звезды в созвездие Овна (гамма Aries), т.е. той, что расположена на роге барана, (JPL, Streete, Rudolphine, Prutenic) или от начального значения прецессии стандартной эпохи (Alfonso от рождества Христова, т.е. от 1.1.1 г., AlKhwarizmi, Toledan от Хиджры, от даты введения мусульманского календаря, т.е. от 15 июля 622 г.). Точками на рисунке отмечено значения прецессии (долгота точки весеннего равноденствия) от первой звезды в созвездие Овна по данным различных авторов (в скобках указаны год и значение прецессии). Птолемей (137 – 6,67), Аль Баттани (880-17,01), Аль Суфи (964-19,53), Аль Бируни (1020-19,67), Омар Хайям (1079-21,1), Насреддин Туси (1270-23,42), Улугбек (1437-26,2), Тихо Браге (1590-27,456), Фламестид (1720-28,9), современные данные (2000-33,2).
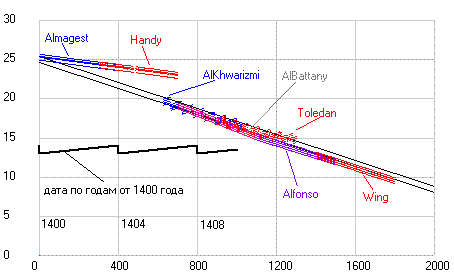
Рис. 17 Даты летнего солнцестояния (по Юлианскому календарю в июне месяце) рассчитанные по таблицам древних астрономов около ориентировочного года создания таблиц. Две черные линии это интервал изменения даты по современным теориям в соответствие со спецификой Юлианского календаря. (Продолжительность года в Юлианском календаре не совпадает с астрономической продолжительностью года и из-за этого дата летнего солнцестояния каждый год смещается примерно на четверть дня, а потом в високосный год возвращается примерно на начальной место, и вследствие этого у меня получаются сразу четыре зависимости по каждой таблице. По этому, чтобы картинка не превратилась в сплошное месиво, я построил графики не на всем интервале от нулевого до 2000 года, а только за 400 лет вблизи примерной даты создания таблиц.)
Как мы видим, фантазия древних астрономов в прогнозировании прецессии была просто безграничной (от линейной зависимости до самых экзотических зависимостей). И, если в Прусских таблицах прецессия увеличивается практически линейно только с небольшими колебаниями по синусоиде (амплитуда 1,19 градуса, период 3400 лет), то в Альфонсовых таблицах принимает ближе к 2000 году явно не линейный характер, а в таблицах AlKhwarizmi и Toledan вообще используется прецессия по теории Курры, т.е. изменяется периодически от хиджры, т.е. от года переселения пророка Мухаммеда из Мекки в Медину (622 год). Причем, если в Толедских таблицах она изменяется по синусоиде, то в таблицах АльХорезми только по положительным половинкам синусоиды (получается почти циклоида).
И хотя теория Куры уже где-то в 13 веке была признана ошибочной, но мы видим, что и в Прусских и в Альфонсовых таблицах прослеживается ее влияние и прецессия в этих таблицах не носит строго линейный характер. Но и линейная зависимость прецессии от времени не является гарантией правильности результатов, т.к., например, Птолемей занизил значение прецессии в 1,5 раза. А кроме разных видов прецессии мы видим у древних астрономов и разные значения долготы первой звезды в созвездие Овна для одного и того же года. Например, европейские астрономы (используя практически одни и те же данные) определяют разное значение долготы этой звезды для стандартной эпохи рождества Христова (мусульманские астрономы используют в качестве стандартной эпохи 14.7.622 года). Так Стрит указывает на 1.1.1. года долготу 6,27 градуса, Кеплер 4,95, а в Альфонсовых таблицах принято 7,85. И это не смотря на то, что Птолемей в его каталоге звезд указывает для 20 июля 137 года долготу Aries = 6,67 градуса.
Но, как следует из приведенных данных, все таблицы (кроме Almagest и Handy), дают удовлетворительные данные по прецессии для того интервала времени, для которого я определял параметры орбиты Земли по наблюдениям за Солнцем. И даже таблицы AlKhwarizmi и Toledan, которые я использовал с 800 по 1100 годы, тоже дают удовлетворительные данные, т.к. синусоида имеет примерно линейный участок от 622 года, от которого, как от стандартной эпохи, она отсчитывается. А время проведения эксперимента при этом я брал таким, чтобы не перейти на следующую ступеньку в синусоиде, т.к. в этих таблицах прецессия изменяется скачкообразно. По этому, и полученные мною ранее по этим таблицам данные, например, по значениям долготы перигелия, которые зависят от прецессии, можно считать соответствующими реальным параметрам орбиты Земли на дату составления таблиц.
В своей программе Solsys7 я использую для корректировки прецессии в таблицах древних астрономов формулы для расчета прецессии из работы [12], которые мало отличаются от данных JPL, а, т.к. на графиках у меня кругом приводятся данные по теориям JPL , я для обозначения современных данных по прецессии использую обозначение JPL. Для сравнения я приведу ниже и формулу Ньюкома [15] (обозначение New) и формулу JPL (в формулах я уберу коэффициенты у dT^3, T1^2 и T1, которые вносят микроскопические поправки, чтобы формулы были читаемыми и по структуре идентичными).
PrecNew = (5025,641 + 2,223 * T1) * dT + 1,072 * dT^2
PrecJPL = (5029,097 + 2,222 * T1) * dT + 1,111 * dT^2
Здесь T1- дата, от которой отсчитывается прецессия, а T2- дата до которой она рассчитывается. И при этом получается dT = T2-T1, а T1 и T2 определяются по формуле
T1, T2 = (JD – JD0) / 36525
Здесь JD – юлианская дата для моментов времени T1 или T2, а JD0(New) = 2415020 и JD0(JPL) = 2451545, т.е. это юлианские даты стандартных эпох J1900 и J2000. Если мы по формулам прецессии будем ее рассчитывать для будущего времени, то dT будет положительным и прецессия тоже будет положительной, а если будем считать в прошлое, то получим отрицательную прецессию. Давайте посчитаем, какая будет по этим формулам прецессия от 2000 года до нулевого.
PrecNew = (5025,641 + 2,223 * (+1)) * (-20) + 1,072 * (+400) = - 100128,48
PrecJPL = (5029,097 + 2,222 * (0)) * (-20) + 1,111 * (+400) = - 100135,57
Соответственно, суммарная прецессия в градусах получится -27,813 и -27,816, а средняя будет 50,00634 и 50,00688 угловых секунд в год. В общем, пользоваться можно как одной, так и другой формулой, т.к. разница будет не большой, как на интервале в 2000 лет, так и для мгновенной прецессии. Например, в 2000 году разница будет (5025,641 + 2,223 * (+1) - 5029,097) / 100 = 0,01233 угловых секунд за год. И, как следует из этих формул, если пренебречь небольшим квадратичным членом, прецессия носит линейный характер и увеличивается на 2,222 угловых секунды в год. И хотя, как мы видим (см. таблицу 12), корректировка прецессии в таблицах древних астрономов дает по сравнению с эфемеридной поправкой не значительное улучшение результатов, но все же, например, в таблицах Птолемея позволяет значительно улучшить время восхода Солнца, от которого идет отсчет времени в описание этого затмения, хотя на положение Луны относительно Солнца это никак не сказывается.
А общий вывод по данным таблиц 11 и 12 можно сделать такой, что, не только, подобрав для прошлого времени эфемеридную поправку, можно для практических расчетов солнечных и лунных затмений пользоваться современными теориями, но при определенной доработке и подобрав свою эфемеридную поправку можно пользоваться и таблицами древних астрономов для настоящего времени. Дело в том, что древние астрономы особое внимание уделяли именно теориям Луны и Солнца, т.к. с их использованием можно рассчитывать солнечные и лунные затмения, но вот теориям планет они уделяли гораздо меньше внимания. Связано это еще и с тем, что создать геоцентрические теории для Луны и Солнца относительно просто, а вот с планетами гораздо сложнее. И результаты таблицы 13, где рассматривается транзит Венеры 8.6.2004 года, подтверждает мой вывод о точности геоцентрических теорий планет древних астрономов (таблицы 17-го века гелиоцентрические). Здесь в геоцентрических таблицах только в Альфонсовых таблицах удается хоть и с ошибкой в один день воспроизвести транзит Венеры. А для таблиц АльБаттани, АльХорезми и Птолемея я указываю только дату и время, когда в экваториальных координатах долгота Венеры была равна долготе Солнца и даю отклонение по широте, которое при этом получилось, т.к. самого транзита мы не наблюдаем вообще.
Таблица 13. Наблюдаемые и расчетные данные транзита Венеры по диску Солнца 8.6.2004 года (наблюдаемые данные по всемирному времени UT взяты здесь http://www.venus2004.org/fr/galerie.php http://www.venus2004.org/comprendre/d/dossier432-1.php?langue=2 http://eclipse.astronomie.info/transit/venus , расчетные данные в топоцентрических экваториальных координатах получены при наблюдение из точки с координатами ObsL=15 и ObsB=50 градусов).
|
Название таблиц, теорий |
Начало |
Конец |
Итого |
|
Наблюдаемые данные |
05:20 – 08.06.2004 |
11:23 – 08.06.2004 |
06:03 |
|
JPL2 ET1=1,2 ET2=0 |
05:17 – 08.06.2004 |
11:24 – 08.06.2004 |
06:07 |
|
JPL0 ET1=1,2 ET2=0 |
05:22 – 08.06.2004 |
11:28 – 08.06.2004 |
06:06 |
|
New0 ET1=1,2 ET2=0 |
05:25 – 08.06.2004 |
11:32 – 08.06.2004 |
06:07 |
|
Wing ET1=0 ET2=0 |
04:12 – 08.06.2004 |
12:04 – 08.06.2004 |
07:52 |
|
Streete ET1=0 ET2=0 |
17:04 – 08.06.2004 |
01:18 – 09.06.2004 |
08:14 |
|
Rudolphine ET1=0 ET2=0 |
00:54 – 07.06.2004 |
15:01 – 07.06.2004 |
04:07 |
|
Alfonso ET1=0 ET2=0 |
13:56 – 09.06.2004 |
21:09 – 09.06.2004 |
07:13 |
|
AlBattany ET1=0 ET2=0 |
dB= -0,4 02:34 – 26.06.2004 |
||
|
AlKhwarizmi ET1=0 ET2=0 |
dB= +6,2 06:00 – 18.05.2004 |
||
|
Almagest ET1=0 ET2=0 |
dB= -0,8 00:56 – 23.06.2004 |
||
Хотя при современных знаниях можно создать и очень точные геоцентрические теории для планет и даже если планеты при этом будут двигаться не по эллипсам, а по эксцентрам (эпициклам) с эквантом. Например, используя мою геометрическую методику определения параметров орбит можно создать геоцентрическую теорию планет, которая будет давать для прошлого результаты даже лучше, чем дают современные теории. Связано это с тем, что в такой теории не нужна будет эфемеридная поправка, которая даже при удачном подборе для одних наблюдательных данных дает значительную ошибку для других данных (см. рис. 15). Да, если мы сравним движение планет по эллипсу с эксцентриситетом 0,2 и по эксцентру с эксцентриситетом 0,4 (что в среднем для планет много), то ошибка будет большой как по углу (максимум 1,7 градуса), так и по расстоянию (максимум 30000 тыс. км). А, если применить движения по эксцентру с эквантом, то эта ошибка уменьшится в несколько раз. Посмотрите на рис.18, где на графике выводится ошибка при движение по простому эксцентру, т.е. без экванта, по сравнению с движением по эллипсу.
Рис. 18 Скриншот формы 14 программы Solsys7 для сравнения движения по эллипсу и по простому эксцентру, т.е. без с экванта. На графике даны отклонения по углу (красные линии) и по расстоянию (синие линии) как для движения по простому эксцентру, так и с эквантом.
И хотя, ошибка даже при движение по эксцентру с эквантом получается для угла максимум 0,6 градуса, а по расстоянию максимум 4000 тыс. км (2,7%), что многовато, но, таких казусов, которые получаются по таблицам древних астрономов для современных наблюдений транзита Венеры по диску Солнца (см. таблицу 13), не будет. Можно конечно и дальше усложнять геоцентрическую теорию уменьшая ошибку и древние астрономы оставили нам богатое наследие различных таких усложнений, а, например, Птолемей применил для движения Меркурия даже эксцентр с двумя фокусами, что уже совсем близко к эллипсу. Но в любом случае теория при этом получится очень сложной для понимания и по этому я не вижу смысла в создании современной геоцентрической теории с использованием кинематической методики и буду делать гелиоцентрическую теорию с движением по эллипсам. Хотя можно сделать и гелиоцентрическую теорию с движением не по эллипсам а по овалам Кассини (отличие от эллипса заключается в том, что неизменным остается не сумма расстояний до двух фокусов, а сумма их квадратов), но при существующих эксцентриситетах орбит планет линии эллипса и овала Кассини практически совпадут и это опять таки только усложнит теорию не добавив ей ничего нового.
А приведенные мною выше хвалебные высказывания в адрес геоцентрических и гелиоцентрических теорий древних астрономов, полученных с использованием геометрической методики, во-первых, являются констатацией того факта, что геометрическую методику создания теорий планет рано списали в запас, а, во-вторых, отдают дань уважения древним астрономам, сумевшим при том уровне развития науки и техники создать вполне работоспособные теории (даже для нашего времени). Конечно же, в древних теориях все обстоит не очень хорошо даже с воспроизведением современных затмений (не говоря уже о транзитах планет), но, как мы видели по данным таблицы 11, и у современных теорий есть проблемы с воспроизведением древних затмений. По этому, для улучшения сходимости наблюдательных данных по затмениям с расчетными данными необходимо не только уточнить современные теории планет, но и пересмотреть все, что связано с замедлением вращения Земли (а возможно и планет вокруг Солнца), а также уточнить теорию Луны. А, в свете рассматриваемого нами вопроса, мы можем со спокойной совестью сказать, как любили писать древние астрономы, - пусть на этом сердце успокоится. И хотя, возможно я еще вернусь к вопросу эфемеридных поправок для физических теорий, но это уже будет отдельное большое исследование, которое надо будет рассматривать как самостоятельную работу не связанную с определением скорости распространения гравитации (в свете которой написана эта статья).
А в этом исследовании мы видим, что не большие отличия в теориях древних астрономов от современных теорий по параметру эксцентриситета орбиты Земли получаются не заметными в практическом плане, например, при расчете солнечных или лунных затмений, но они очень существенны для нас в теоретическом плане для определения скорости гравитации. Именно по этому я так долго старался согласовать теории древних астрономов с современными теориями по параметру эксцентриситета орбиты Земли, а удалось это сделать только благодаря бесценным данным по равноденствиям Гиппарха. И только после разрешения противоречия по древним и современным теориям я могу со спокойной совестью приступать к определению по вековым смещениям параметров орбит планет скорости распространения гравитации. Конкретно я планирую нахождение скорости распространения гравитации производить по вековым смещениям параметров орбит за последние 200 лет (примерно линейная зависимость и данные наблюдений не вызывают больших вопросов), а потом произведу проверку полученной мною динамической (физической) теории по вековым смещениям параметров орбит за период в 2000 лет, где смещения будут уже явно не линейными. О том, что из этого получится, Вы узнаете в следующей статье, а о промежуточных результатах я как всегда буду сообщать на форумах. И в заключение хочу выразить благодарность Сергею Хартикову (модератор Астрофорума) и Вадиму Чазову (сотрудник ГАИШ) за оказанную помощь при рассмотрение некоторых специфических вопросов по астрономии.
Список использованной литературы
1. - К.Птолемей //Альмагест или математическое сочинение в тринадцати книгах// http://naturalhistory.narod.ru/Person/Antic/Ptolemey/Almag_ogl.htm
http://hbar.phys.msu.ru/gorm/almagest/text/book.htm
http://www.astromyth.tau-site.ru/books/almagest.djvu
http://ilib.mirror1.mccme.ru/djvu/klassik/almagest.djvu
2.- Аль Беруни //Канон Масуда// Книга 6.
3. – Р.Ньютон //Преступление Клавдия Птолемея// http://portvein777.narod.ru/DATA/editor_forew.htm
http://hbar.phys.msu.ru/gorm/almagest/almanewt.htm
4.- Курс лекций А.И.Еремеевой по истории и методологии астрономии http://fsf.tsu.ru/science/aspirant/aspirant/ref.pdf не качает
5.-Таблицы древних астрономов оформленные в виде таблиц Excel 2003 с сайта автора этих файлов http://www.thep.lu.se/~larsg/astromodels.zip http://home.thep.lu.se/~larsg/download.html
(файлы адаптированные мною для русскоязычного Excel http://modsys.narod.ru/Arhiv/astromodels_ser.zip и конвертер дат Египетского календаря использующегося в таблицах Птолемея и его таблицы на Java Script http://www.phys.uu.nl/~vgent/astro/almagestephemeris.htm )
6.- Н.И.Идельсон //Этюды по истории планетных теорий// http://naturalhistory.narod.ru/Person/Lib/Idelson/Index.htm
7.- Riccioli Giovanni Battista //Astronomiae reformatae tomi duo, quorum prior observationes, hypotheses et fundamenta tabularum, posterior praecepta pro vsu Tabularum Astronomicarum, et ipsas Tabulas Astronomicas CII., continet. Prioris tomi in decem libros diuisi, Argumenta Pagina sequenti exponuntur//.
http://visualiseur.bnf.fr/CadresFenetre?O=NUMM-51331&M=pagination&Y=Image
8. -В.А.Бронштейн //Клавдий Птолемей// http://naturalhistory.narod.ru/Person/Antic/Ptolemey/Bron_16.htm
9. – Б.А.Розенфельд, М.И.Рожанская, З.К.Соколовская //Абу-р-Райхан ал-Бируни// http://naturalhistory.narod.ru/Person/Lib/Biruni/Index.htm
10. – А.Ахмедов // О «Зидже» Аль Хорезми// http://naturalhistory.narod.ru/Person/Srednevek/Horezmi/Horezmi_Ogl.htm
11. – T.Streete //A new theorie of the celestial motions, London, 1661// и комментарий Ларса Гислена http://www.thep.lu.se/~larsg/Streete.zip
12. – О.Монтенбрук, Т.Пфлегер Астрономия с персональным компьютером, М.:Мир, 1993.
13. – Н.Т.Роузвер, Перигелий Меркурия. От Леверье до Эйнштейна: Пер. с англ. – М. : Мир, 1985. – 246 с. ( http://bourabai.kz/articles/roseveare/index.htm - некоторые фрагменты этого текста связанные с формулами не до конца отредактированы).
14. – E.Myles Standish and James G.Williams. //Orbital Ephemerides of the Sun, Moon, and Planets// http://iau-comm4.jpl.nasa.gov/XSChap8.pdf
(в переводе Вадима Чазова http://vadimchazov.narod.ru/text_htm/xsru00.htm )
15. – Г.Н.Дубошин Справочное руководство по небесной механике и астродинамике. 2-е изд. М. : Наука, 1976. – 864 c. http://www.astrolib.ru/files/6/Duboshin-Sprav_Ruk_po_Neb_Meh.pdf
16. - Юдин С.Ю. Моделирование систем и оптимизация их параметров. - Волгоград: Электронный вариант книги (http://modsys.narod.ru/ ), 2003. - 208с.