Эксперимент Майкельсона-Морли

МЕХАНИКА ДЛЯ КВАНТОВОЙ МЕХАНИКИ

Часть 8. Об Эксперименте Майкельсона-Морли

первая редакция 02.02.2022

С. Ю. Юдин http://modsys.narod.ru . . modsys@yandex.ru

Аннотация 1

Введение 2

1. Исторический обзор экспериментов выполненных на установке Майкельсона 4

2. Математическая модель установки Майкельсона 12

3. Математическая модель установки Юдина 24

4. Теория интерференции 27

5. Теоретическая проверка результатов выполненных на установке Майкельсона 43

6. Исследования выполненные на установке Юдина 52

Выводы 70

Список литературы 71

Послесловие 73

Аннотация

Анализ конструкции интерферометра Майкельсона, показал, что он совершенно не пригоден для обнаружения эфирного ветра, как в научном плане, так и в техническом, т.к. данная конструкция в научном плане не позволяет обнаружить полупериодический эффект, для обнаружения которого этот интерферометр и создавался, а в техническом плане не позволяет задать нужные параметры установки, чтобы, зная их, правильно интерпретировать полученный результат. К тому же и теория этого эксперимента оказалась совершенно не пригодной для интерпретации полученных экспериментальных данных, т.к. смещение полос в этом эксперименте должно происходить не от разности времени движения двух лучей от источника света до экрана, которая практически никак не влияет на смещение полос, а в первую очередь от разности координат падения двух лучей на экран и от эффекта Доплера. Поэтому мне пришлось с нуля создавать свою теорию этого эксперимента и практически с нуля теорию интерференции, т.к. то, что написано по этой теории в учебниках не выдерживает никакой критики. Ведь даже сами авторы учебников пишут, что их теория интерференции нарушает закон сохранения энергии, а их объяснение почему это допустимо достойно юмористической передачи, а не учебников.

А, используя свою теорию интерференции, я смог не только объяснить почему все экспериментаторы получали смещения полос меньше, чем ожидали, но и показал, что кроме обычных полос, которые мы можем наблюдать, например, при интерференции на тонких пленках, на этом интерферометре могли наблюдаться и, как я их назвал, "составные" полосы. При этом эффект Доплера приводит к смещению полос при малейшей скорости вращения экспериментальной установки и этот периодический эффект многократно превосходит по величине полупериодический эффект от различных направлений движения установки. Учитывая основные недостатки конструкции интерферометра Майкельсона, я создал свою конструкцию интерферометра для определения абсолютной скорости Земли, которая является симметричной и поэтому на ней должен наблюдаться именно полупериодический эффект. К сожалению, и в моей конструкции интерферометра наблюдается эффект Доплера не только от линейного движения прибора, но и при его повороте, а поэтому практически невозможно из общего смещения полос выделить именно то, что объясняется различным направлением движения установки. К тому же в математических моделях своей установки и установки Майкельсона я не предусмотрел учет эффекта Доплера от вращения установки и поэтому вынужден сейчас прекратить дальнейшие исследования. Но после того, как я придумаю способ точной фиксации смещения полос при различных направлениях движения своей установки, я продолжу это исследование.

Ключевые слова - эксперимент Майкельсона-Морли, теория интерференции, эффект Доплера, опровержение СТО.

Введение.

Эксперимент Майкельсона-Морли, который был выполнен этими учеными в 1887 году и является повторением эксперимента Майкельсона, который он выполнил в 1881 году, является одним из самых известных физических экспериментов, который в корне изменил все дальнейшее развитие физики, т.к. его результат позволил Пуанкаре и Лоренцу создавать математические химеры, которые уже не воспринимались учеными как фантазии оторванные от реальности. Да, конечно же, основы для создания этих математических химер заложил Лагранж, который свой сложный математический метод уменьшения уравнений, описывающих механические системы, сумел значительно упростить, используя экстремали Эйлера и его математическую интерпретацию принципа наименьшего действия, который считался тогда научным физическим принципом. И, в результате, как написал Герц, "к концу 19 столетия физика отдала предпочтение другому способу мышления". А в конечном итоге это вылилось в то, что Эйнштейн, упростив до уровня обывателя понятие математических химер Пуанкаре и Лоренца, создал теорию относительности, где допускались любые фантазии, т.к. чисто математически их можно было обосновать. Ну, а потом тот же Эйнштейн, опираясь на математическую химеру Планка, создает и так называемую квантовую механику, в которой нет никакой механики, а есть только статистика.

О глупостях Эйнштейна в его теории относительности, которые он обильно разбросал в своих многочисленных статьях, я подробно написал в своей статье "О принципах относительности", где опровергаю эти его глупости не только логически, но и многочисленными вычислительными экспериментами. Ну, а разбор того как же Эйнштейн сформулировал свой знаменитый принцип относительности является апофеозом литературного творчества Эйнштейна, т.к. в конце концов он, как унтер-офицерская вдова, сам себя и высек, сформулировав при создание общей теории относительности (ОТО) этот принцип так, что он в этой формулировке хоронит свою специальную (частную) теорию относительности (СТО), которая и является именно теорией относительности, т.к. ОТО не имеет к ней никакого отношения, а является одной из многих теорий гравитации, которая построена на совсем другом принципе. Очень подробно я написал в своей статье "О формуле Планка и кванте действия" и о творчестве другого мошенника, где наглядно показал, что формула Вина, в которой Планк добавил ничего не значащую единичку и потом назвал ее своей формулой, не только не очень удачно аппроксимирует экспериментальные данные, но и не содержит в себе никакой научной основы, т.к. статистика это не раздел физики, а раздел математики. Ну, а откровения Планка, где он напрямую пишет, что занимался просто подгонкой решения под нужный результат и при этом даже изобрел нужную ему формулу энтропии, назвав ее именем Больцмана, чтобы все думали, что изобрел ее Больцман, окончательно ставят крест на том, что его формула имеет какое-то отношение к науке.

Ну, а вот сейчас я решил разобраться и с творчеством Майкельсона и конкретно с теорией его эксперимента известного как эксперимент Майкельсона-Морли. Вообще-то, теория этого эксперимента, которая должна была объяснять результаты получающиеся при проведении натурного эксперимента, была настолько безграмотной, что у меня даже язык не поворачивается назвать ее теорией (при этом я ни сколько не хочу умолять заслуг Майкельсона, как инженера). Но в то время маховик, запущенный Лагранжем, набирал обороты и основная масса ученых стремилась быть в мейнстриме того времени "сказку сделать былью", т.е. описать все физические явления исходя из чистой математики, вооружившись различными лагранжианами и принципом наименьшего действия, а на физическую сторону явлений стали мало обращать внимания. Например, еще в 1927 году Хедрик на конференции в Калифорнии, где Майкельсон, Лоренц, Миллер и другие обсуждали результаты экспериментов различных авторов на установках собранных по схеме Майкельсона, опираясь на работу Риги, сделал доклад о том, что при движение зеркал угол отражения будет не такой как в статике и привел формулу для расчета "эффективного" угла наклона зеркал. А так же он сообщил о том, что этот эффект должен привести к тому, что при повороте установки полосы и не должны смещаться, т.е. эта поправка полностью перечеркивала теорию Майкельсона.

Поэтому, естественно, ни кто и не подумал вносить эту поправку в теорию этого эксперимента, т.к. интерпретация его результатов с использованием существующей теории этого эксперимента, созданной Майкельсоном, полностью устраивала математико-физиков, которые к тому времени окончательно задушили физику в своих объятиях. И здесь у меня вызывает вопросы позиция самого Майкельсона, который до конца своих дней считал, что Земля движется сквозь неподвижный эфир, но ничего не сделал для того, чтобы улучшить свою теорию эксперимента, которая бы показала, что в его экспериментах и не должно было наблюдаться смещение полос в интерферометре. Ведь он отлично знал и об аберрации света и об изменении угла наклона движущихся зеркал, т.к. они с Морли писали об этом в дополнение к своей статье 1887 года. Естественно, что он знал и об эффекте Доплера и поэтому мог бы все это учесть в своей модернизированной теории эксперимента, а он вместо этого в дополнение к статье стал предлагать новые конструкции приборов, которые бы позволили определить скорость Земли в неподвижном эфире. Единственное объяснение такого его поведения, которое ко мне приходит на ум, это то, что наверное это оказалось для него слишком сложно сделать чисто математически.

Поэтому, я первым делом постарался создать максимально адекватную математическую модель установки Майкельсона, на которой он проводил свои натурные эксперименты, а так же добавил в теорию этого эксперимента свой расчет интерференционной картинки, которая должна получаться на экране при падение на него двух лучей света с теми параметрами (скорость, частота, фаза, время движения, угол падения), которые получаются при проведении вычислительного эксперимента на математической модели установки. Ну, и, естественно, я сам выполнил несколько натурных экспериментов на установке собранной по схеме Майкельсона, чтобы иметь представление о том, что могли наблюдать ученые, проводившие на ней натурные эксперименты. А, убедившись в полной бесполезности установки, собранной по этой схеме для проведения научных исследований, я разработал свою схему установки для проведения натурных экспериментов, которые могут обнаружить движение Земли сквозь неподвижный эфир, в котором распространяются все взаимодействия между телами и различные излучения, например, свет.

Да, и моя установка пока не позволила обнаружить это движение, но за счет того, что она позволяет проводить на ней именно научные исследования, т.к. первоначальная схема предложенной мною установки позволяет значительно изменять эту схему для проведения узко направленных экспериментов. При этом, моя установка позволяет с удовлетворительной точностью задавать углы наклона зеркал и влиять на параметры лучей света на отдельных этапах их пути от лазера до экрана, а установка по схеме Майкельсона не позволяет этого сделать и, следовательно, приходится только гадать каковы были эти параметры. Надеюсь, что мне сейчас удастся так модернизировать мою установку, что она все таки позволит отделить полупериодический эффект от периодического эффекта и тогда можно будет на ней проводить натурные эксперименты по определению абсолютной скорости Земли. Ну, а многочисленные вычислительные эксперименты выполненные мною на математической модели установки по схеме Майкельсона, позволили сделать однозначный вывод, что в натурных экспериментах на этой установке мы и не должны были наблюдать заметного смещения интерференционных полос при движение всей установки вместе с Землей в различных направлениях. Таким образом, эти вычислительные эксперименты подтвердили результаты полученные различными авторами при проведение натурных экспериментов на этой установке. И, следовательно, никаких объективных причин для создания теории относительности как не существовало, так и не существует сейчас. А все эксперименты, выполненные после создания теории относительности, доказывают ее справедливость только при неправильной интерпретации полученных результатов, как, например, все эксперименты по доказательству релятивистской формулы эффекта Доплера, которые я подробно рассмотрел в своей статье "эффект Доплера".

1. Исторический обзор экспериментов выполненных на установке Майкельсона.

Вообще-то, первоначально этот эксперимент задумывался для определения скорости света, но трактовка результатов этого эксперимента привела к тому, что он теперь рассматривается как эксперимент по определению абсолютной скорости Земли в неподвижном эфире, сквозь который она движется. Ведь до этого эксперимента в науке было веками устоявшееся мнение, что все тела движутся сквозь неподвижный эфир. Правда, до этого были и другие эксперименты, например, Физо, которые говорили о том, что все не так однозначно и возможно, что эфир увлекается движущимися телами или полностью или частично, но само существование неподвижного эфира при этом ни кем не оспаривалось. Вот только ученые конца 19-го и начала 20-го века не правильно интерпретировали результаты экспериментов Майкельсона, Физо и других подобных им, а в результате была создана теория относительности, которая отрицает возможность определения абсолютных скоростей, хотя для вращательного движения еще Ньютон доказал, что это возможно и теоретически и практически. Здесь надо сразу сказать, что и в течение всего 20-го века предпринимались попытки определить абсолютную скорость Земли с использованием интерферометра Майкельсона, но опять таки с теми же теоретическими ошибками, которые не позволяли этого сделать.

Сначала Майкельсон выполнил в 1881 году эксперимент на своей установке интерферометра один [1], а затем в 1887 году на усовершенствованной установке совместно с Морли [2]. Однако самый заметный практический вклад по проведению этого эксперимента внес, конечно-же, Миллер [3]. Он не только проводил эти эксперименты на протяжении нескольких десятилетий, но его эксперименты являются самыми корректными из всех выполнявшихся на установке Майкельсона когда либо. А проводили этот эксперимент десятки различных ученых, которые изменяли длину плеч интерферометра, откачивали воздух из колб, где двигались лучи, совершенствовали оптическую систему и т.д., но суть эксперимента оставалась одна и та же. И результаты они при этом получали опять таки практически одни и те же, где у них теоретические значения смещений полос в интерферометре никак не соответствовали наблюдаемым значениям при той теории эксперимента, которую они все использовали. Некоторые из этих результатов я привожу ниже, где экспериментальные значения в разных отчетах немного отличаются от приведенных мною. При этом Демьянов [4] при проведении в 60-х годах экспериментов, использовал свой вариант установки, где на обратном пути лучи двигались по другой траектории (или в воздухе, как и у всех до него, или в воде), а так же он рассчитывал смещение полос по своей формуле.

Таблица 1. Результаты по смещению интерференционных полос при развороте установки на 180 градусов полученные различными авторами на установке Майкельсона.

Автор и год______________суммарная длина плеча______теория________эксперимент

Майкельсон 1881_________________1,2_________________0,04_________0,004...0,015

Майкельсон и Морли 1887_________11,0________________0,4__________0,005...0,010

Морли и Миллер 1902...1906_______32,2________________1,13__________0,007...0,015

Миллер 1921...1924_______________32,0________________1,12__________0,007...0,040

Миллер 1925...1926_______________32,0________________1,12_____________0,044

Демьянов 1968 (воздух)____________3,0_________________0,01_____________0,01

Демьянов 1971 (вода)_____________0,15_________________0,085____________0,11

Суть эксперимента Майкельсона иллюстрирует рис. 1a, где свет от источника Q направляется на полупрозрачное стекло (а можно сказать полупрозрачное зеркало) M, т.е. на стеклянную пластину немного посеребренную сверху, которое делит его на два луча расходящиеся под углом 90 градусов. Один луч идет к одному зеркалу S1, а второй к другому зеркалу S2, где они отражаются и опять попадают на полупрозрачное зеркало M, а затем опять вместе попадают в объектив зрительной трубы F, где мы наблюдаем интерференционную картину. При этом первый (горизонтальный) луч трижды проходит через полупрозрачное зеркало M, где скорость света в стекле меньше, чем в воздухе, а второй луч только один раз, и поэтому на пути второго луча помещают стеклянную пластину P, которую он проходит два раза. А, т.к. толщина этой пластины такая же, как и у пластины полупрозрачного зеркала M, получается, что, при равенстве горизонтального и вертикального участков пути, которые называют плечами интерферометра, время движения лучей при покоящейся установке должно быть одинаковое. Здесь зеркала S1 и S2 и полупрозрачное зеркало M показаны в двух положениях. Положения S1, S2 и M соответствуют моменту разделения луча света от источника Q на два луча, а положения S1", S2" и M" моментам времени, когда лучи касались этих поверхностей при движении всей установки вправо.

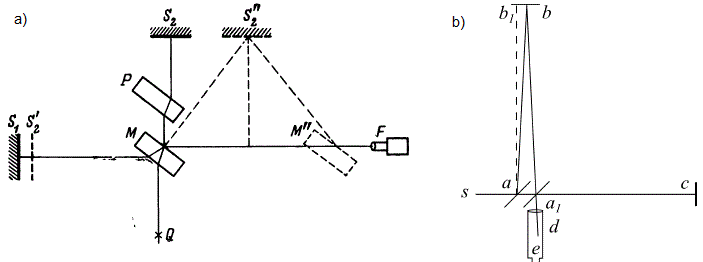
Рис. 1. Схема эксперимента Майкельсона-Морли a) - воспроизведено из работы [5] и схема этого эксперимента приведенная в работе самих авторов b) - воспроизведено из работы [2].

И, исходя из того, что при разном направлении движения всей установки у нас будет разность времени движения двух лучей до экрана, теоретики этого эксперимента делали вывод о том, что при этом должна быть разность фаз двух лучей, попадающих на экран (или в объектив телескопа). А, следовательно, при повороте установки на 90 или 180 градусов мы должны наблюдать сдвиг полос возникающих при явлении интерференции двух лучей, т.к. эти лучи у нас получены делением одного и того же луча источника света и, следовательно, они когерентны. Да, теория этого эксперимента неоднократно критиковалась и во времена самого Майкельсона и продолжает критиковаться сейчас, но адекватной теории этого эксперимента я так и не видел. Например, как пишет Франкфурт [5], Потье уже в том же 1881 году указал Майкельсону на то, что ".. в опыте не учтено движение зеркала вместе с Землей. Майкельсон внес исправления и получил результат в два раза меньше". И тот же Франкфурт [5] пишет, что "Лоренц считает, что опыт Майкельсона не опровергает его теорию. Он показывает, что действительное значение смещения должно быть вдвое меньшим, чем было указано, и попадало бы в область ошибок, а это значит, что если бы и был эфирный ветер меньше 30 км/с (как следует по Лоренцу), то Майкельсон его бы не обнаружил.". А, т.к. научный авторитет Лоренца в то время был очень большим, то и теорию этого эксперимента стали частенько называть теорией Лоренца.

В общем отношение к эксперименту Майкельсона было тогда мягко говоря очень прохладным. Поэтому в 1887 году он повторил свой эксперимент совместно с Морли на усовершенствованной установке и с теорией эксперимента, которая учитывала сделанные выше замечания и давала результат смещения полос в два раза меньше чем его теория 1881 года. А вся теория эксперимента у него отражается двумя уравнениями для времени движения двух лучей (Т1 для горизонтального и Т2 для вертикального) от пластины М до зеркал и обратно в туже точку на пластине М по формулам (1.1) для 1881 года и по формулам (1.2) для 1887 года, где L это длина плеч интерферометра, т.е. расстояние от центра пластины М до зеркал, а V и Vs это скорости установки и света в абсолютной системе отсчета (АСО), т.е. в неподвижном эфире.

T1= 2*L*Vs / (Vs^2 - V^2)

T2= 2*L / Vs (1.1)

T1= 2*L*Vs / (Vs^2 - V^2)

T2= (2*L / Vs) * [1 + V^2 / (2*Vs^2)] (1.2)

В расчете 1881 года он принял, что при движении установки в АСО вправо вертикальный луч будет двигаться строго перпендикулярно горизонтальному лучу и упадет в туже точку на стеклянной пластине М откуда он вылетел, т.к. в расчетах он использовал одинаковый путь L проходимый лучами в ИСО установки. Но эту ошибку элементарно заметить, т.к. вертикальный луч, если будет двигаться строго вертикально, не вернется в туже точку на стеклянной пластине М, т.к. она за время его движения сместится вправо, как это показано на рис. 1a. А вот, если мы примем, что вертикальный луч, вылетев из стеклянной пластины М, будет двигаться так, как это изображено на рис.1a, то уравнения 1.2 действительно будут теперь правильно отражать время движения двух лучей. И здесь остается только один вопрос - с какого перепугу вертикальный луч, если он упал на стеклянную пластину снизу строго вертикально, вылетит из нее сверху под углом, а не строго вертикально. А вот ответа на этот вопрос я ни у кого не видел. И поэтому, как я предполагаю, мы и видим у разных авторов разное описание этого эксперимента. До этого мы рассматривали схему эксперимента 1881 года на рис. 1a, которую дал Франкфурт (исходя из чисто словесного описания данного эксперимента Майкельсоном в его работе 1881 года, т.к. там он не привел схему расположения элементов установки в разные моменты времени), но уже с исправлением, которое позволяет вертикальному лучу вернуться в ту же точку на пластине М.

А на рис.1b мы видим несколько другую схему, которую привели в своей работе Майкельсон и Морли в 1887 году, где мы видим, что в отличие от описания на рис. 1a у них источник света расположен не внизу, а слева. Но это все равно ничего не меняет принципиально, т.к. и здесь мы видим, что горизонтальный луч, двигаясь от источника света "s" строго горизонтально к стеклянной пластине "а", которая тоже движется вправо, затем вылетает из нее, к зеркалу "с" строго вдоль оси X, а вот вертикальный луч, отразившись от стеклянной пластины "а" и летящий к зеркалу "b" движется почему-то не строго вдоль оси Y. Т.е. и тут остается тот же вопрос - с какого перепугу вертикальный луч, если он упал на стеклянную пластину слева строго горизонтально, отразился от нее не строго вертикально, хотя угол наклона пластины 45 градусов. Я здесь пока не останавливаюсь на подробностях всего этого процесса, т.к. луч, влетающий в пластину, сначала преломляется и потом под другим углом падает на пластину и отражается, а затем при выходе из пластины опять преломляется. Но в результате он вылетит из пластины под углом отражения, который будет равен углу падения луча влетающего в пластину. Поэтому тут та же проблема, что и со схемой на рис. 1a, хотя Майкельсон с Морли и попытались ее замаскировать, т.к. анализировать эту проблему по их рисунку сложнее.

Да, чисто теоретически можно добиться того, чтобы в схеме, например, на рис. 1a вертикальный луч вернулся на пластину М в ту же точку, откуда вылетел. Для этого надо, например, наклонить зеркало от которого он отражается, но при движении всей установки влево зеркало надо будет опять таки развернуть в другую сторону, что практически не осуществимо. При этом, тоже самое надо будет делать и с траекторией горизонтального луча, если у нас установка будет двигаться вертикально, т.е. надо будет верхнее зеркало вернуть в исходное положение, а разворачивать левое зеркало, что тем более не осуществимо. Правда, тут есть и другой вариант добиться того, чтобы вертикальный луч вернулся на пластину М в ту же точку, откуда вылетел. Для этого надо изменить прицельный угол, но в таком случае у нас и луч двигающийся горизонтально, тоже, упав на пластину М не под углом 45 градусов, будет двигаться не строго горизонтально. Более того, при движении всей установки влево, у нас должен быть уже другой прицельный угол и его надо будет постоянно изменять при повороте установки, что не возможно сделать практически.

Здесь частично помог бы учет аберрации луча света, т.к. при ее учете не надо крутить никакие зеркала, а знак прицельного угла изменялся бы автоматически при движении установки или влево или вправо (луч отклонялся бы на рис. 1а в сторону движения установки). Да это решает проблему траектории вертикального луча, но при этом горизонтальный луч, отразившись от пластины М, двигался бы уже не горизонтально, т.е. мы видим, что нет физического объяснения чисто математической теории этого эксперимента и поэтому она никак не может быть использована для объяснения результатов полученных в этом эксперименте. Следовательно, теорию этого эксперимента нам придется создавать самим, а для этого посмотрим что еще писали о теории этого эксперимента. Например, как я уже упоминал, Хедрик [6], опираясь на работы Риги, предложил учесть то, что при движении зеркал их эффективные углы наклона будут отличаться от углов наклона в статическом положении, т.е. отражение света будет происходить немного под другими углами. А я бы развил предложение Хедрика и сделал предположение, что и преломление света в движущихся пластинах тоже будет происходить при немного других углах наклона этих пластин, чем это наблюдается в статике. Хотя, как пишет Дрюков [20], который рассматривает пробелы в теории преломления и отражения света, выясняется, что в этих явлениях пока не все объяснено строго научно даже при покоящихся стеклах и зеркалах. Так что остается только надеяться, что существующее теоретическое описание этих явлений не дает значительной погрешности для наших экспериментов.

К замечаниям по теории этого эксперимента можно еще добавить и то, что скорость света будет изменятся при движении в средах с разной оптической плотностью, а последняя в свою очередь будет зависеть от частоты света, т.е. желательно бы учесть и дисперсию. А так же надо будет обязательно учесть аберрацию луча источника света, т.к. даже, если расположить источник и линзу, которая фокусирует свет от него в узкий пучок, строго вертикально, то, при движении установки вправо, луч будет вылетать из линзы отклоненным в правую сторону. Ну и, конечно же, в теории этого эксперимента надо учесть эффект Доплера, т.к. ни кто не будет оспаривать тот факт, что свет в лучах, отражаясь от движущихся поверхностей, будет изменять свою частоту и, следовательно, на участках, где он движется, при одинаковом времени движения свет сделает разное количество колебаний. А это в конечном итоге отразится на том сколько сделает колебаний свет в двух лучах пока они долетят от источника света до экрана, что должно напрямую влиять на фазы лучей в момент их падения на экран и следовательно на положения интерференционных полос.

Более того, разная частота света в двух лучах, падающих на экран, приведет к тому, что полосы будут постоянно смещаться в одну сторону даже, если мы не вращаем установку. И о таком смещении полос пишут практически все, кто проводил натурные эксперименты на установке Майкельсона. Но это постоянное смещение полос все экспериментаторы считали просто погрешностью измерений и различными статистическими методами устраняли эту, как им казалось, систематическую погрешность. И только в работах последнего времени, например, в работах [7, 8, 10] говорится о том, что в теории этого эксперимента обязательно надо учесть явление эффекта Доплера. Вот только о том как его учесть при многократном переотражение света от движущихся поверхностей ни кто не пишет. И здесь только работа [7] заметно отличаются от общего мейнстрима не менее бестолковой, чем сам этот эксперимент, критики. Здесь авторы не только сделали грамотный обзор известных работ по этому эксперименту и сделали подробный разбор ошибок в теории эксперимента Майкельсона, но и попытались учесть влияние разности частоты света двух лучей, принятых поверхностью экрана, на результаты эксперимента, что позволило им даже получить по данным Миллера (см. рис.2) скорость Земли 1365 км/с.

Здесь на графике скачки смещений соответствуют моментам времени когда при наблюдении центральная полоса смещалась слишком далеко от центра окуляра и Миллер клал на одно из плеч интерферометра грузик, чтобы плечо сдеформировалось и полосы сместились назад. Поэтому я могу в отличие от авторов работы [7] объяснить постоянное смещение полос и деформацией конструкции установки. Ведь их установки были очень громоздкими и тяжелыми. Кстати, я и сам наблюдал заметное постоянное смещение полос в покоящейся установке своей конструкции после того как я производил регулировку зеркал, но со временем остаточные деформации в креплениях зеркал пропадали и полосы переставали смещаться. Поэтому все эксперименты я выполнял только, если после последней регулировки зеркал прошли сутки и интерференционная картинка не испортилась. И на записях экспериментов на моей покоящейся установке, которые я проводил непрерывно в течение нескольких часов, а иногда и суток, например, вот в этом файле [22], я наблюдал только незначительное смещение полос то в одну то в другую сторону, что можно объяснить небольшими колебаниями температура в подвале, где я проводил эксперименты.

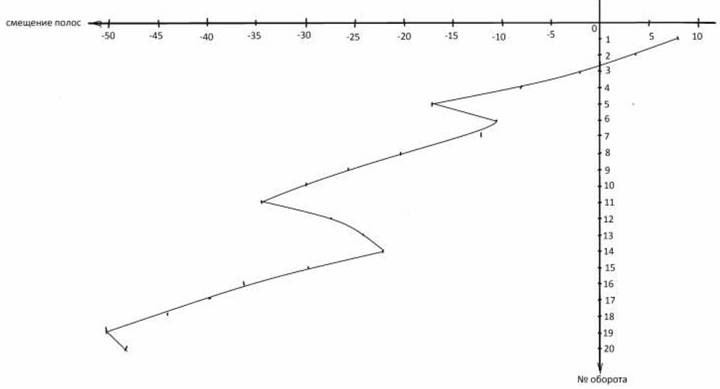
Рис.2. График смещения полос в десятых долях их ширины в интерферометре Майкельсона за время его поворота на 20 оборотов (примерно 14 минут) построенный по данным экспериментов Миллера. Воспроизведено из работы [7].

Поэтому я сделал запись положения полос в течение двух с половиной часов и на покоящейся установке Майкельсона [23], когда после регулировки зеркал прошло несколько суток, и в результате я увидел, что полосы все равно сместились в одну сторону на 9 полос. А такой результат можно объяснить не остаточными деформациями в элементах установки, а только другими эффектами, например, температурными расширениями деталей крепления зеркал, т.к. при весьма значительной тепловой (инфракрасной) мощности натриевых горелок, которые применялись ранее, вполне могло происходить значительное нагревание зеркал и их креплений. Но я применял маломощный лазер (5 милливатт), который не мог значительно нагреть зеркала, а вот то, что я для подсветки установки при записи на вэбкамеру ее положения поместил под установкой лампу накаливания 60 ватт, это вполне могло привести к температурным деформациям. Тогда я решил повторить этот эксперимент без подсветки установки и у меня получилось смещение полос максимум на 1-у полосу в течение двух часов непрерывной записи [24]. Поэтому я пока не буду делать окончательных выводов по поводу постоянного смещения полос в установке Майкельсона. Тем более, что, во-первых, экспериментировал я с ней очень мало, а, во-вторых, эффект Доплера оказался очень сложно поддающимся описанию при многократном переотражение света от движущихся поверхностей и у меня нет пока уверенности в том, что принятая экраном частота света в двух лучах будет разной, а не будет равна частоте лазера.

А вот как учесть эффект Доплера именно в теории Майкельсона я нашел в работе [10], где автор правильно пишет о том, что надо учитывать не только время движения двух лучей, но и их индивидуальную частоту, которая будет разной в горизонтальном и в вертикальном лучах. Ведь только тогда у нас получится правильно рассчитать разность фаз двух лучей падающих на экран. К сожалению, на этом положительные замечания по этой работе кончаются, т.к. далее идут сплошные глупости. При этом автор статьи при подгонке решения задачи под нужный результат переплюнул даже таких мошенников как Планк и Эйнштейн и сумел получить, используя данные наблюдений Майкельсона с Морли и Миллера, значения скорости Земли, соответственно, 32,2 км/с и 29,97 км/с, что в 4-е раза больше, чем получили сами авторы этих экспериментальных данных. А сделал он это очень просто - заявил, что Майкельсон не правильно рассчитал в своей теории эксперимента суммарное количество колебаний света в двух лучах по времени движения лучей с постоянной частотой на всех участках их путей до экрана, т.к. ошибочно использовал в расчете частоту в два раза больше реальной частоты. Это сразу дало ему результат в два раза больше, чем было в теории Майкельсона. Затем, он заявил, что на самом деле смещение полос будет в два раза больше, чем наблюдалось в эксперименте и в результате, найденная экспериментаторами скорость Земли, т.е. примерно в 7,5 км/с, превратилась у него в 30 км/с.

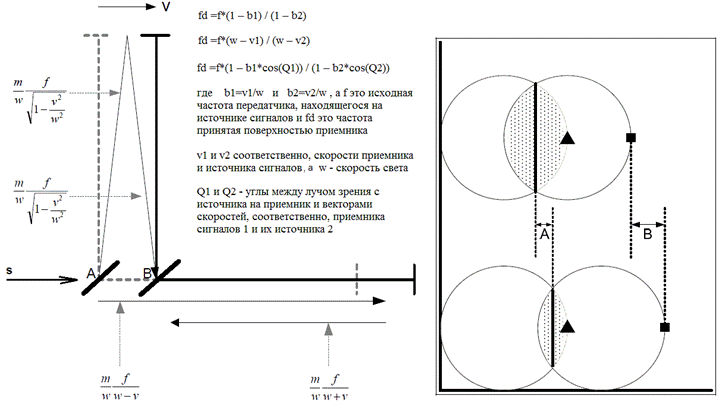
Рис. 3. Слева схема к расчету по теории Майкельсона (см. схему на рис. 1b) с указанием количества колебаний света в лучах , которое пропорционально частоте света в лучах согласно его формулам (1), (2) и (5) для расчета эффекта Доплера (воспроизведено из работы [10]), где я дорисовал положение полупрозрачной пластины в точках A и B, когда лучи вылетели из нее и когда они вернулись к ней, а также источник света s и добавил текст с формулой Лоренца для расчета эффекта Доплера (сверху две эквивалентные формулы для продольного эффекта, а ниже для общего случая). Справа реальное и наблюдаемое смещение интерференционных полос, объясняемое смещением пятен двух лучей при их падение на экран (воспроизведено так же из работы [10]).

А сейчас давайте посмотрим на научный уровень знаний этого сказочника, который полученным результатом не хотел опровергать СТО, как может показаться некоторым читателям, т.к. СТО предсказывает нулевое смещение интерференционных полос, а хотел своим расчетом именно подтвердить правильность СТО, но в своей трактовке. Давайте начнем с того, как же этот грамотей определил частоту света в горизонтальном луче летящем вправо и после отражения от зеркала влево. Исходя из его формул на рис. 3 получается, что частота света от источника s, просто пройдя напрямую через полупрозрачное стекло почему то стала больше f (здесь у него f это не частота передатчика, а уже частота света, летящего к полупрозрачной пластине, т.е. уже излученная движущимся источником s). Ведь даже, если мы рассмотрим согласно формулам эффекта Доплера процесс переизлучения света полупрозрачной пластиной, то у нас частота принятая пластиной, как приемником, будет f1= f * (w-v), а частота излученная пластиной, как источником, будет f2= f1 / (w-v)= f * (w-v) / (w-v)= f. А теперь давайте рассмотрим частоту света в луче отраженном от зеркала. Здесь частота света принятая поверхностью зеркала будет опять f1= f * (w-v), а частота излученная зеркалом, как источником, будет f2= f1 / (w+v)= f*(w-v) / (w+v). Здесь в знаменателе будет +v, т.к. cos(180)= -1, т.е. и эта частота у него рассчитана не правильно.

Таким образом, мы видим, что формулы (1), (2) и (5) примененные Брайном в его работе для расчета эффекта Доплера, которые, с учетом примененных им коэффициентов, превратились в количество колебаний света на отдельных участках пути лучей, не имеют к эффекту Доплера никакого отношения, а просто повторяют формулы Майкельсона для времени (или пути) пройденного лучами, но в хитрой интерпретации Брайна. И в результате этих хитрых пересчетов Брайн заявил, что Майкельсон, определяя разность фаз двух лучей, завысил это расчетное значение в два раза, т.к. завысил в два раза частоту, используемую в расчете. А далее он рассматривает правый рис. 3, где он смещение линии пересечения двух световых пятен лучей на экране объявляет наблюдаемым положением интерференционных полос и заявляет, что, т.к. сами пятна сместились в два раза дальше, чем линия пересечения пятен, то, следовательно, расчетное значение смещения интерференционных полос было тоже завышено Майкельсоном в два раза. Да, смещение пятен падения лучей на экран оказывает влияние на смещение полос, но не то о котором пишет Брайн, который оказывается слабо разбирается и в интерференции. А далее, суммируя два своих вывода, Брайн заявляет, что расчетное значение смещения полос было завышено Майкельсоном в 4-е раза, а при том смещении, что наблюдалось в экспериментах, у нас получается скорость Земли в 4-е раза больше, чем заявили авторы этих экспериментов. Вот на таком научном уровне подтверждается экспериментально справедливость не только новых релятивистских теорий, как у Брайна, но и теории относительности в изложении Эйнштейна. Хотя, вынужден признать, что научный уровень Эйнштейна был все таки выше. Вот только, к сожалению, таких специалистов создавать релятивистские теории, как Эйнштейн и Брайн, хватает и среди специалистов, создающих эфирные теории.

К критике теории эксперимента Майкельсона пожалуй следует отнести и некоторые недостатки самой установки, т.к. они влияют на выводы сделанные при любой теории этого эксперимента. Например, многие авторы писали о том, что во время проведения эксперимента самопроизвольно изменялась ширина полос видимых в окуляре телескопа (примеры фотографий полос даны на рис. 4 слева). А это приводило к тому, что даже полосы, которые на самом деле не смещались, смещались в окуляре трубы телескопа при изменении их ширины и из этого можно было сделать вывод, что произошло смещение первоначальных полс, т.е. с первоначальной их шириной, а не с видимой сейчас. Более того, как пишет Миллер [3] во всех экспериментах наблюдалось не только смещение полос при повороте установки на 180 градусов, т.е. наблюдался полупериодический эффект, но и смещение полос при повороте установки на 360 градусов, т.е. полнопериодический эффект. Что касается первого эффекта, то именно он и должен был наблюдаться согласно теории этого эксперимента, поэтому тут вроде все логично, но вот откуда взялся второй эффект это для всех экспериментаторов было загадкой. Причем, как пишет Миллер, смещение полос при этом эффекте было тем больше, чем были уже наблюдаемые полосы, и он даже приводит эту зависимость (см. рис. 4 справа). Но как бы оно там ни было, а этот эффект значительно искажает результаты наблюдений даже, если мы при обработке данных скорректируем их на этот эффект. Поэтому я считаю саму схему интерферометра Майкельсона теоретически не правильной.

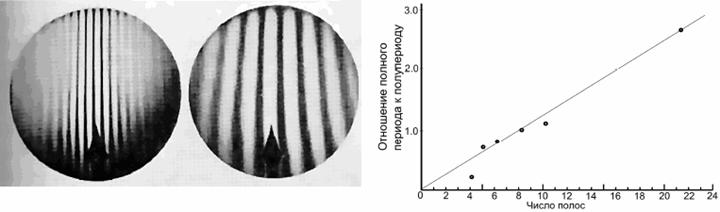
Рис. 4. Интерференционные полосы наблюдавшиеся в окуляре телескопа при неизвестных углах наклона зеркал (слева) и влияние числа наблюдаемых при проведение экспериментов в окуляре полос на величину смещения полос от полнопериодического эффекта (справа). Воспроизведено из работы [3].

И, конечно же, я считаю огромным недостатком интерферометра Майкельсона то, что мы не можем не только определить ширину полос, наблюдаемых в экспериментах, и то в какую сторону они должны смещаться, но мы даже не можем сказать какие это полосы - обычные или, как я их назвал, составные, а это тоже влияет на результат. Подробно о составных полосах я расскажу позже, а сейчас просто скажу, что при моментальной фотографии они состоят из нескольких отдельных полос, которые очень быстро движутся в пределах ширины этой полосы и поэтому мы визуально воспринимаем их как обычные сплошные полосы. Да, я согласен, что у многих авторов экспериментов с интерферометром Майкельсона не было в то время лазеров, видеокамер и компьютеров, которые позволяют значительно уменьшить погрешности измерений в экспериментах, но от неправильной теории эксперимента, как и от неграмотной конструкции интерферометра не спасут никакие компьютеры. Поэтому, хотя группа ученых из Колумбийского университета [9] и провела в 2003...2005 году повтор эксперимента Майкельсона-Морли с использованием современных приборов и с записью данных наблюдений в файлы, но полученные ими данные все равно не согласуются с теорией этого эксперимента созданной Майкельсоном. А, заканчивая обзор рассмотренных нами экспериментов, выполненных на установке Майкельсона, надо сделать однозначный вывод о том, что все экспериментаторы наблюдали какое-то смещение полос, обусловленное абсолютной скоростью движения Земли сквозь неподвижный эфир, но правильно интерпретировать полученные ими данные не смогли.

2. Математическая модель установки Майкельсона

Прежде, чем приступить к описанию математической модели установки Майкельсона, я дам свои определения таким понятиям, как модель, математическая модель и вычислительный эксперимент. Под моделью следует понимать копию объекта, находящуюся с ним в определенном объективном соответствии, способную замещать его на определенных этапах познания и практической деятельности человека и дающую при ее исследовании информацию о самом моделируемом объекте, т.е. об оригинале. При этом под объектом в смысле объективной реальности следует понимать различные системы: механические, физические, биологические, социально-экономические и т.д., а под системой следует понимать ограниченное множество элементов объединенных причинно-следственными и функциональными связями, позволяющими ей функционировать определенным образом. И, если охарактеризовать объект с точки зрения теории отражения, то он подвергается внутренним и внешним воздействиям и реагирует на них изменением своего состояния в виде различных показателей работы (показателей функционирования).

Но не надо путать модели с имитаторами (симуляторами), которые тоже являются копиями объекта, но в отличие от моделей, они не могут замещать объект при его познании и, следовательно, не могут дать новой информации о самом объекте, а могут только выдать уже известную информацию, но в другом виде. Таким образом, имитаторы могут быть использованы только для оптимизации параметров систем и только в тех условиях, при которых они были получены. Т.е. с помощью моделей можно проводить как синтез систем, так и их анализ, а с помощью имитаторов, только синтез. Это объясняется тем, что, например, математические имитаторы не раскрывают сущности явлений, т.е. их взаимную внутреннюю связь, а только выдают формальный результат, который должен получиться при функционировании системы. А вот математические модели отражают объективное влияние параметров системы на показатели ее функционирования вследствие внутренней логики объекта. Т.е. в отличие от моделей, где отражена и форма и содержание, в имитаторах, в общем случае, отражена только форма. При этом наличие в математических моделях логической структуры позволяет не только прогнозировать показатели работы системы, но и экстраполировать выводы, вытекающие из структуры модели, на структуру самого объекта.

Математические модели это количественные идеальные модели, которые построены на принципах стандартной логики и в их основе всегда лежат законы. Если в их основе заложены объективные законы, т.е. законы природы, то данная модель всегда обладает прогностической функцией, т.е. с помощью нее мы можем уверенно прогнозировать будущее. Если же в математической модели имеются как объективные, так и субъективные законы, т.е. законы поведения человека или законы налогового кодекса, то прогнозировать будущее с помощью таких математических моделей можно только с какой-то вероятностью в расчете на то, что эти законы либо не будут меняться, либо будут меняться по известным нам правилам.

Природа, при проявлении тех или иных эффектов, не решает уравнения, описывающие различные явления, и не создает в зависимости от того, какое будет решение, тот или иной внешний эффект, т.е. результат этого решения. Она просто воспроизводит эти явления и нужные эффекты проявляются сами. Поэтому все эффекты, которые могут проявиться в объекте, можно воспроизвести и с помощью численного решения системы уравнений, составляющих математическую модель объекта, когда не ищут ответы на конкретные вопросы, как при аналитическом решении, а просто воспроизводят отдельные явления природы по этим уравнениям. И, если при совместном решении этих уравнений должен проявиться тот или иной эффект, то он обязательно и проявится, например, явление резонанса, хотя в самом уравнении, описывающем ускорения груза, подвешенного на пружинке, при воздействие на него внешней периодической силы нет формулы отражающей явление резонанса. И в этом смысле математическая модель это заменитель природы и каков будет ответ математической модели до проведения на ней вычислительного эксперимента не знает даже создатель этой модели.

Таким образом, вычислительный эксперимент это такой же эксперимент как и на самом объекте, но только не натурный, а вычислительный, т.е. выполненный на математической модели этого объекта. При этом даже натурный эксперимент не обязательно выполнять на самом объекте и с гораздо меньшими затратами (при удовлетворительной точности данных) мы можем получить нужные результаты, проведя натурный эксперимент на материальной модели. Например, при определение аэродинамического сопротивления самолета, мы можем продувать в аэродинамической трубе не сам самолет, а его уменьшенную копию, т.е. материальную модель, используя при этом свойство масштабности. Но, гораздо больше информации и гораздо больше возможностей мы получаем, экспериментируя не с материальной моделью, а с идеальной моделью и конкретно с математической. Ну, а более подробно о классификации различных моделей и имитаторов вы можете посмотреть в моей статье "Модели и имитаторы" [11], чтобы вы не путали модели с имитаторами, т.е. симуляторами, т.е. симулянтами выдающими себя за модели.

Таким образом, при создании математической модели установки Майкельсона наша задача состоит в том, чтобы грамотно описать с математической точки зрения все явления природы, которые будут наблюдаться при проведении натурного эксперимента на этой установке. И, как я уже писал выше, нам надо учесть следующие явления природы

- аберрацию луча лазера, т.е. его отклонение от геометрической оси лазера при движении лазера в направлении перпендикулярном оси лазера.

- изменение скорости света при его движении в средах разной оптической плотности

- отражение света от движущихся зеркал

- преломление света в движущихся стеклах

- эффект Доплера при отражении света от движущихся зеркал

Выше я упоминал еще и о дисперсии, т.е. о влиянии частоты света на оптическую плотность среды и как следствие на скорость света в этой среде, но сейчас я убрал моделирование этого явления из уже созданной математической модели, т.к. в процессе ее тестирования возникли вопросы по самой частоте отраженной от движущихся поверхностей. К тому же сам этот эффект дисперсии очень незначительный и заметно проявляется пожалуй только в сигналах от пульсаров, где излучение разной частоты проходит от пульсаров до Земли очень большие расстояния и поэтому мы фиксируем заметное расхождение во времени прихода сигналов разной частоты. А вот о явлении звездной аберрации, которую чаще всего называют просто аберрацией, т.е. искажением видимого положения источника света, мы все знаем по наблюдениям за звездами в телескоп, который движется вместе с Землей. Здесь, чтобы увидеть свет от звезд, который будет проходить путь от объектива до окуляра, нам надо немного наклонять телескоп по ходу движения Земли, чтобы свет мог пройти этот путь в трубе. И тоже самое нам надо будет сделать, например, с отрезком обычной трубы, если мы хотим, чтобы капли дождя, которые падают вертикально, пролетели сквозь эту трубу, если мы вместе с трубой быстро движемся на автомобиле.

Так вот, тоже самое происходит и со светом, который проходит от лазерного диода до линзы, которая фокусирует луч, например, в дешевых китайских лазерных модулях, которые я использовал в натурных экспериментах. К сожалению, аберрация луча лазера воспринимается очень трудно и поэтому я остановлюсь на этом вопросе подробно. Если бы у нас не было аберрации луча лазера, т.е. луч вылетал бы из него строго вдоль геометрической оси лазера, то мы в простейшем эксперименте при повороте лазера на 180 градусов наблюдали бы смещение его луча на экране при движение лазера вместе с Землей со скоростью 30 км/с то в одном направлении относительно неподвижного эфира, то в другом. Это наглядно демонстрирует схема на рис. 5, где у нас показаны положения лазера и экрана, на который падает его луч, в двух положениях. В положении 0 луч вылетает из лазера, а в положении 1 он достигает экрана. Если бы вся экспериментальная установка двигалась вертикально, т.е. под углом А=90 градусов, как это отражено на среднем рисунке, то у нас бы не было никакого смещения луча относительно середины экрана. Но, если установка будет двигаться или вправо А=0 или влево А=180, как это отражено на крайних рисунках, то за то время пока луч будет лететь в АСО от лазера до экрана последний сдвинется в сторону и мы увидим на экране смещение луча или влево или вправо относительно центра экрана, т.е. луч у нас как бы будет отклонятся на угол В или влево или вправо.

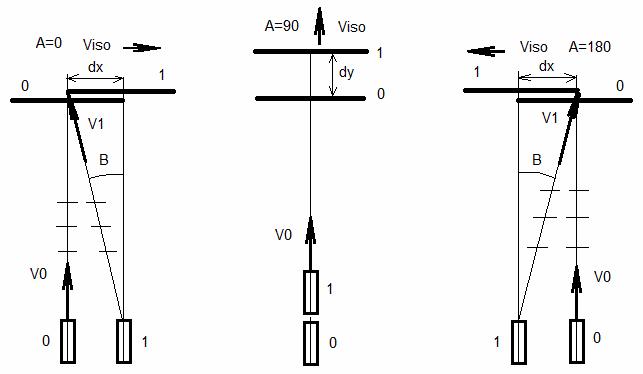
Рис. 5. Схема движения луча лазера, вылетающего из него строго вдоль геометрической оси лазера, при разной скорости движения экспериментальной установки в неподвижном эфире.

Чтобы проверить это, я выполнил простейший эксперимент, где разместил на вращающейся платформе лазер и на расстоянии 1,9 м от него экран, роль которого выполняла вэбкамера (без оптики) с размером матрицы по ширине 5,8 мм. А, чтобы не сжечь матрицу вэбкамеры, я поместил после лазера светофильтр, который ослаблял яркость луча, и на экране ноутбука я видел вот такое изображение пятна лазера, а запись изображение при вращение установки вы можете посмотреть в видеофайле [25].

Рис.6. Изображение на матрице вэбкамеры пятна луча лазера.

Как видно из видеофайла записи этого эксперимента, где установка делает несколько оборотов, никакого смещения пятна по экрану не происходит, а согласно расчету по схеме на рис. 5 пятно должно было смещаться на 0,19 мм, т.е. на 3,25 % от ширины экрана в одну сторону и на столько же в другую. При разрешении матрицы 3 мкм/ пиксель и при размерах матрицы 1920*1080 пикселей суммарное смещение пятна в двух крайних положениях должно было составить 125 пикселей, что не возможно не заметить. Но в видеофайле мы видим, что пятно стоит как вкопанное и если бы не изменение освещенности экрана, когда при вращении установки на матрицу падал свет от лампочки освещения, то можно было бы подумать, что это не видео, а фотография. Поэтому я даже в конце эксперимента резко остановил вращение установки, чтобы изображение закачалось. А объяснение такого результата должно быть таким. Свет от светодиода, расположенного в фокусе линзы идет до нее как сферическая волна, а потом выходит из нее узким почти параллельным пучком, который отклоняться от вертикального направления, как это изображено на рис. 7.

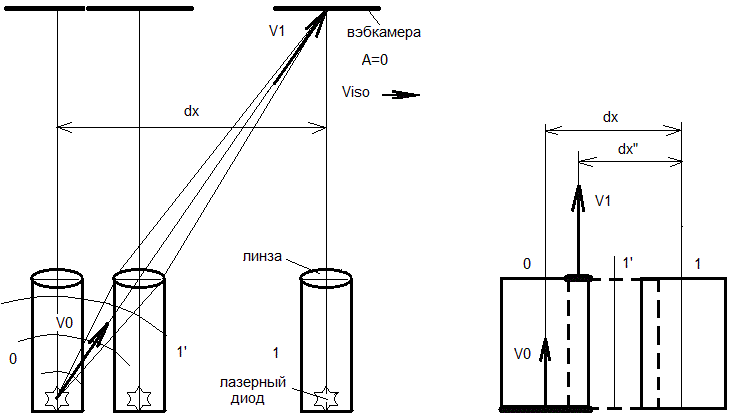
Рис.7. Движение луча лазера при движение всей установки вправо перпендикулярно геометрической оси лазера. От точечного источника создающего сферические волны через линзу (левый рисунок) и плоских волн от нижнего торца цилиндра лазера (правый рисунок).

Я, к сожалению, не специалист в геометрической оптике, поэтому могу только предположить, что все будет так, как изображено на этом рисунке (на левой схеме), где гомоцентрический пучок лучей света (т.е. в нем все лучи сходятся в одной точке), преобразуется линзой опять в гомоцентрический пучок лучей. Здесь получается, что в момент времени dt', когда фронт сферической волны от светодиода достигнет линзы лазерного модуля, и сам лазер и вэбкамера будут в положении 1', нам надо использовать в расчетах направление скорости луча V0 при вылете из светодиода на центр линзы, а тогда и дальше при вылете из линзы скорость луча V1 будет направлена в центр матрицы вэбкамеры. И таким образом за время dt, когда луч достигнет вэбкамеры, вся установка сместится относительно неподвижного эфира на расстояние dx и на матрице мы и не должны будем зафиксировать никакого смещения пятна лазера. Здесь надо заметить, что вообще-то в расчете сделанном мною для плоских волн, вылетающих строго вдоль геометрической оси лазера на рис. 5, смещение пятна лазера должно быть немного меньше 6,5% от ширины матрицы, т.к. согласно правому рис.7 у нас не весь фронт плоской волны при движение лазера вправо или влево будет вылетать из него.

В этом случае лазер вместе с вэбкамерой точно также будет изображен в трех положениях 0, 1' (лазер нарисован пунктирной линией) и 1, а фронты волн света будут двигаться в эфире, т.е. в АСО, вдоль геометрической оси лазера. Вот только в положении 1' у нас не весь фронт волны, вылетевший со скоростью V0 от нижнего торца лазера, сможет вылететь из лазера, а только его часть, т.к. часть луча упрется в левую стенку цилиндра. А вылетевшая часть луча со скоростью V1 продолжит путь до вэбкамеры. А, когда она ее достигнет, то это уменьшенное пятно лазера будет смещено относительно центра матрицы вэбкамеры на расстояние dx", что будет немного меньше расстояния dx, которое было мною рассчитано выше по рис. 5. Но в любом случае хоть какое-то смещение мы должны были при этом наблюдать, а кроме того при этом должен был изменяться размер пятна, т.к. при А=90 у нас на экране должно было быть полное изображение пятна, а при А=0 и А=180 только его часть. Вот только ничего этого я не наблюдал, а, следовательно, надо принять, что во всех экспериментах, где луч света формируется с использованием оптики от точечного источника в узконаправленный пучок, у нас всегда будет аберрация луча источника света. И при этом угол отклонения луча лазера будет определятся так же, как и при аберрации на телескопе, т.е. тангенс этого угла будет равен отношению скорости лазера к скорости света.

Теперь давайте рассмотрим явление изменения эффективного угла наклона зеркал при их движении. Здесь так же, как и при покоящихся зеркалах, угол падения будет равен углу отражения, но рассчитываться эти углы будут не относительно угла наклона зеркал в статике, а относительно эффективного угла наклона зеркал, который при их движении будет зависеть от скорости движения зеркал. Как я уже писал, одним из первых на этот эффект обратил внимание Хедрик [6] на конференции по эксперименту Майкельсона-Морли, где он привел и формулы для расчета этого эффективного угла. И в этом явлении нет ничего необычного, т.к. , например, и угол отскока мяча от движущейся поверхности тоже не равен этому углу при отскоке от покоящейся поверхности, хотя физика данного явления и будет совсем другой. А какова физика нашего явления демонстрирует левый рис. 8, где показано, что, когда один край плоской волны касается зеркала или стекла, плоскость которых не перпендикулярна направлению движения луча света и при этом она движется, то другой край коснется этой поверхности не одновременно с первым краем. Здесь фронт волны AZ движется вправо и зеркало AL тоже движется вправо. В данный момент времени поверхности зеркала коснулся нижний край фронта волны, а через время dt, когда зеркало сместится на расстояние v*dt в положение A'L' и верхний край фронта волны пройдет расстояние c*dt и тоже коснется поверхности зеркала. Таким образом для плоской волны эффективный угол наклона зеркала α определится по двум точкам в пространстве A и L'. Аналогично, если фронт будет падать с правой стороны, то эффективный угол наклона зеркала будет γ.

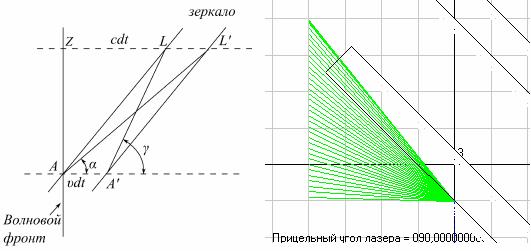
Рис.8. Падение фронта плоской волны на поверхность движущегося зеркала. Левый рисунок воспроизведен из работы [6], а правый это скриншот программы Maikelson1.

Я создавая свою математическую модель решил не полагаться на различные известные формулы, а именно моделировать все физические эффекты и поэтому смоделировал и процесс падения фронта волны на движущиеся поверхности, как это отражено на правом рис. 8. Здесь фронт волны движется снизу вверх и падает на движущееся вверх полупрозрачное зеркало 3, которое изображено в момент, когда его коснулся правый фронт волны. А далее в программе моделируется одновременное движение со своими скоростями зеркала и левого края фронта волны до тех пор пока левый край фронта не коснется поверхности зеркала. Но на рисунок при анимации выводится только текущее положение левого края фронта, которое соединяется зеленой линией с точкой в пространстве, где правый край фронта волны коснулся зеркала. И после определения эффективного угла в момент касания лучом зеркала дальнейшая анимация движения лучей и зеркал начнется именно с того места, где правый край фронта коснулся поверхности зеркала, за который принимается точка в пространстве, где центр этого луча коснулся поверхности зеркала. При этом заданная для анимации ширина зеркала никак не влияет на сам расчет, т.к. движение левого края фронта продолжается до тех пор пока не станет минимальным расстояние между точкой (край фронта) и линией поверхности зеркала заданной уравнением прямой.

После выполнения нескольких тестовых расчетов на математической модели я получил при скорости зеркала V=3000 м/с и скорости света в вакууме Vs=30000 м/с (при его движении в воздухе снизу вверх) результаты приведенные в таблице ниже. При этом угол наклона зеркала 3 в статике был Alfa3=135 градусов, а основной шаг решения уравнений был 1*10^-7 с, который для повышения точности расчета при приближении лучей света к зеркалам и стеклам уменьшался еще в 1*10^5 раз. Затем я сравнил полученные мною результаты с теми, что получаются по формулам (2.1), приведенным Хедриком в работе [6]. Как видим, по этим формулам эффект получается близким к тому, что я получил при моделировании процесса падения плоской волны на движущееся зеркало. Но при наших реальных расчетах, где, хотя отношение скорости Земли к скорости света будет не 0,1 как в тестовом примере, а 0,001, т.е. разница в углах будет в 100 раз меньше, расхождение с расчетом по формулам (2-1) все равно я считаю большими, т.к. при реальной частоте света 4,614*10^14 Гц, что в 10^8 раз больше частоты в тестовом примере, даже незначительные отклонения в угле отражения приведут к заметному отклонению в путях, пройденных лучами, и в координатах падения лучей на экран. Поэтому я для проверки получающихся у меня результатов при моделировании этого процесса решил сам вывести формулы (2-2) для расчета динамических углов наклона зеркал AlfaZ в простейших случаях, когда они движутся строго или вдоль движения лучей или перпендикулярно этому направлению.

Таблица 2. Эффективные углы наклона зеркала AlfaZ в тестовом примере, полученные при моделировании процесса падения фронта волны на движущееся зеркало и при аналитическом расчете по формулам, которые я получил сам (2-2) и которые приведены в работе Хедрика (2-1), для случаев движения зеркала и фронта волны или вдоль одной прямой или в перпендикулярных направлениях. При движение установки вдоль оси X углы ее скорости будут 0 и 180 градусов, а вдоль оси Y 90 и 270.

Угол скорости зеркала____________0_______________90____________180_____________270

Численное решение__________131,986263______131,986263_____137,727091______137, 727091

Аналитическое Юдин________131,986263______131,986263_____137,727089______137, 727089

Аналитическое Хедрик_______132,272911______132,272911_____138,013737______138,013737

AlfaZ = arctan(tan(Alfa3) * (1 + VYiso / Vs)) если установка движется вдоль оси Y (2-1)

AlfaZ = arctan(tan(Alfa3) * (1 - VXiso / Vs)) если установка движется вдоль оси Х при Alfa3 < pi / 2

AlfaZ = arctan(tan(Alfa3) * (1 + VXiso / Vs)) если установка движется вдоль оси Х при Alfa3 > pi / 2

Y2 = (X2 - X1) * tan(Alfa3) / (1 + tan(Alfa3) * VXiso / Vs) если установка движется вдоль оси Х

Y2 = Vs * (X2 - X1) * tan(Alfa3) / (Vs - VYiso) если установка движется вдоль оси Y

AlfaZ = arctan(Y2 / (X2 - X1)) (2-2)

А вот здесь мы видим полное совпадение моих аналитических расчетов с численным решением, полученным при моделировании процесса падения фронта волны на движущееся зеркало. Но, при углах движения 180 и 270 градусов у нас получилась погрешность численного расчета в 9-ой значащей цифре, что объясняется тем, что при моделирование этого процесса в приведенном тестовом примере моменты касания краями фронта волны поверхности зеркала определялись по расстоянию края фронта волны до поверхности зеркала с точностью L1*4,614*10^-6, где L1=6,5*10^-3 м длина волны света в этом примере. Да, точность численного решения всегда можно повысить уменьшив шаг решения, но делать это можно до определенного предела, т.к. при очень большом количестве циклов расчета погрешность расчета за счет мусора, который появляется за счет округления последней значащей цифры или на +1 или на -1, может перейти и на предпоследнюю значащую цифру и т.д. А у меня программа Maikelson1 написана на языке программирования Visual Basic 6.0, у которого последней значащей цифрой для данных Double является 15-я цифра. Поэтому при моделировании движения реального света с частотой 4,614*10^14 Гц и длиной волны 650 нм нам обязательно надо будет выполнить несколько тестовых расчетов, чтобы убедиться, что численное решение с заданным шагом решения не приводит к заметным погрешностям связанным с округлением данных в последней значащей цифре.

Здесь многие могут сказать - а зачем производить моделирование процесса падения плоской волны на движущуюся поверхность, если эффективный угол можно рассчитать аналитически. Да, в каких то простейших явлениях я так и делаю, но для этого процесса я не смог получить аналитические формулы расчета угла AlfaZ при произвольном направлении скорости движения зеркала. Но, даже, если бы я их и получил, то мне все равно надо бы было убедиться, что в них нет ошибки, а узнать это мы можем только смоделировав этот процесс. Ведь именно после этого выяснилось, что формулы (2-1) содержат какую то ошибку. Поэтому я в своих моделях всегда стараюсь именно смоделировать какое то отдельное явление, хотя модель не перестает быть моделью, если отдельные явления в ней не смоделированы, а получающийся при этом результат получен по аналитическим формулам. Ну, а что касается эффекта Доплера при многократном переотражение волн от движущихся поверхностей, то мы убедимся, что там пока только моделирование этого процесса может нам дать нужный результат, т.к. пока не существует вообще никаких аналитических формул для описания этого процесса.

А теперь, после того как мы рассмотрели и явление аберрации луча света и изменения угла наклона движущихся зеркал, давайте рассмотрим как эти два явления проявят себя совместно в установке Майкельсона. Сначала давайте рассмотрим на рис. 9 левую схему движения луча, т.е. при движение всей установки со скоростью Viso вправо, и таким образом повторим эксперимент по сносу луча лазера эфирным ветром, как это мы рассматривали на рис. 5. Здесь у нас нулевой результат, который и в этом случае получен мною такого натурного эксперимента, нельзя объяснить аберрацией луча лазера согласно рис.7, т.к. здесь аберрации не будет. Но теперь у нас будет изменение угла наклона движущегося зеркала и поэтому луч света, отразившись от движущегося зеркала, полетит к вэбкамере не под углом A=90 градусов, а под углом A=89,9943 градуса. И, следовательно, когда он достигнет вэбкамеры на расстоянии 1,9 метра, то сместится относительно начального положения вэбкамеры 0, когда и зеркало было в положении 0, вправо на 0,19 мм. Но за это время и сама вэбкамера в положение 1 сместится вправо на 0,19 мм и таким образом луч упадет на матрицу вэбкамеры в тоже самое место, куда он падал при покоящейся установке, т.е. при Viso=0, т.е. никакого смещения пятна лазера на матрице вэбкамеры не должно быть и в этом эксперименте. Аналогично будет и при движении установки в АСО влево, когда луч будет смещаться влево. Т.е. данный результат не может быть объяснен аберрацией луча лазера, как это предполагалось на рис. 7, но теперь он объясняется изменением угла наклона движущегося зеркала.

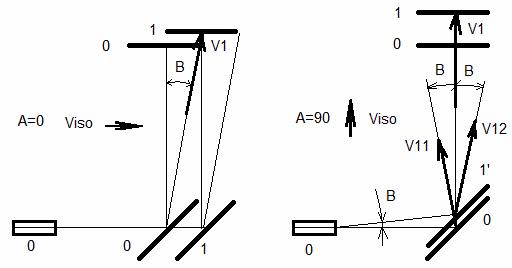
Рис. 9. Совместное действие эффектов аберрации луча лазера и изменения угла наклона движущегося зеркала в установке Майкельсона.

И теперь давайте посмотрим, что дадут эти два эффекта для схемы установки Майкельсона. Здесь при движении установки вправо, как это и отражено на схеме рис. 1b и на левом рис. 9, горизонтальный луч будет двигаться строго горизонтально, а вертикальный луч за счет изменения угла наклона движущейся полупрозрачной пластины действительно отразится от нее так, что полетит вверх немного наклоненным по ходу движения установки и поэтому, отразившись от верхнего зеркала упадет в ту же точку откуда вылетел. А при движении установки вверх у нас теперь уже горизонтальный луч за счет аберрации не только упадет на полупрозрачную пластину не строго горизонтально, а под углом В, но и далее, вылетев из нее, тоже полетит под тем же углом, а, следовательно, когда пластина сместится вверх, он все равно, отразившись от правого зеркала, упадет на пластину в ту же точку откуда вылетел. Но теперь у нас вертикальный луч, отразившись от полупрозрачной пластины, должен полететь не строго вертикально, а в направлении V12, а нам согласно теории Майкельсона надо, чтобы он отразившись полетел строго вертикально. Это достигается за счет того, что у нас и в этом случае изменится угол наклона движущегося зеркала, который здесь станет больше 45 градусов, и за счет этого луч должен был отразиться в направлении скорости V11. А, т.к. у нас численно получается, что здесь угол аберрации равен изменению статического угла наклона зеркала, то от одного эффекта луч должен будет отклониться на угол B вправо, а от другого на угол B влево, и в результате луч полетит строго вертикально, как того и требует теория этого эксперимента созданная Майкельсоном. И, естественно, что и в этом случае мы опять не обнаружим сноса луча лазера эфирным ветром при этом движении установки, т.к. это будет соответствовать средней схеме на рис.5.

А теперь давайте посмотрим как все эти эффекты отразятся на параметрах двух лучей в установке Майкельсона при движении его установки в разных направлениях. Для этого проведем вычислительные эксперименты на математической модели, которую я оформил в виде компьютерной программы Maikelson1. Здесь у меня луч света от лазера 5 вылетает в направление полупрозрачной стеклянной пластины 3, а затем проходит через эту пластину и на верхней ее поверхности, которая является полупрозрачной, делится на два луча. Левый горизонтальный луч 1 отражается от верхней стороны пластины, проходит сквозь нее и затем выйдя из нее летит к зеркалу 1, где он отражается, а затем опять проходит через пластину 3 и выйдя из нее летит в сторону экрана (или трубы телескопа) 6. А вертикальный луч проходит через пластину 3 и летит к компенсационной стеклянной пластине 4, которая в этой схеме компенсирует тройной проход горизонтального луча через пластину 3, а затем, выйдя из нее, летит к зеркалу 2 и, отразившись от него, опять проходит пластину 4 и попав на пластину 3 отражается от нее в сторону экрана. И на рис. 10 приведен скриншоты программы Maikelson1, где на рисунок выводится анимация движения элементов установки и двух лучей, но, т.к. при анимации в программе предыдущие положения элементов установки стираются, то стираются и уже нарисованные траектории движения лучей, которые пересекают движущиеся элементы установки, поэтому на рис. 10 я в этих экспериментах отключил анимацию, чтобы на рисунок выводились только траектории движения лучей от лазера до экрана. Но при этом положения поверхностей стекол, расположенных под эффективными углами наклона, когда их поверхностей касаются лучи света, на рисунок выводятся (зеленые линии) и поэтому вы можете видеть и положения элементов установки в эти моменты времени.

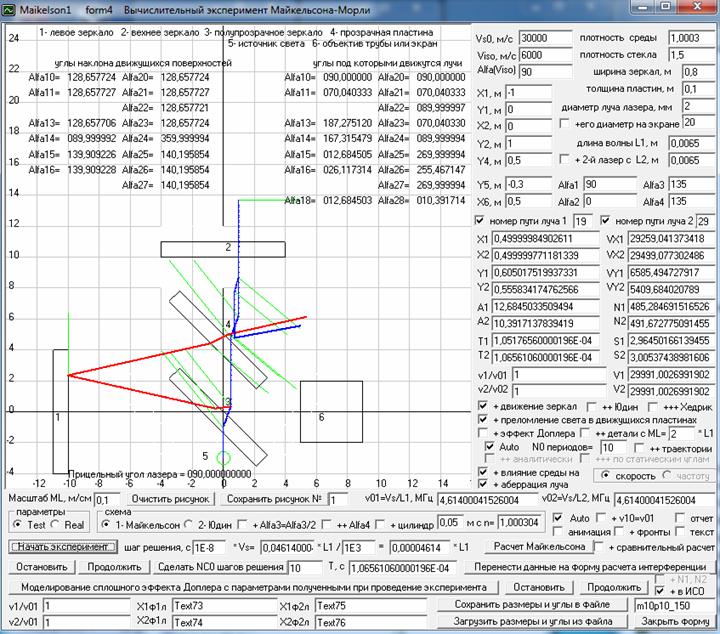
Рис. 10. Траектории движения двух лучей света от лазера до экрана в установке по схеме Майкельсона при ее движение вверх, где положение элементов установки показано в момент вылета лучей из лазера. Скриншот программы Maikelson1, где индексы у углов, приведенных в верхней части рисунка, соответствуют следующим участкам путей, пройденных двумя лучами.

ii = 10 и jj = 20 общий путь до стеклянной поверхности наклонного полупрозрачного зеркала 3 и преломление

ii = 11 движение внутри наклонного полупрозрачного зеркала 3 и отражение

ii = 12 нет

ii = 13 движение внутри наклонного полупрозрачного зеркала 3 влево и преломление

ii = 14 движение свободно влево и отражение от зеркала 1

ii = 15 движение свободно вправо и преломление на пластине 3

ii = 16 движение внутри наклонного полупрозрачного зеркала 3 вправо и преломление

ii = 17 нет

ii = 18 движение свободно вправо до приемника

jj = 21 движение внутри наклонного полупрозрачного зеркала 3 и преломление

jj = 22 движение свободно в вверх и преломление на прозрачной пластине 4

jj = 23 движение внутри прозрачной пластины 4 вверх и преломление

jj = 24 движение свободно в вверх и отражение от зеркала 2

jj = 25 движение свободно вниз и преломление на прозрачной пластине 4

jj = 26 движение внутри прозрачной пластины 4 вниз и преломление

jj = 27 движение свободно вниз и отражение от наклонного зеркала 3

jj = 28 свободно вправо до приемника

В этом тестовом вычислительном эксперименте, чтобы даже визуально было видно различие в траектории движения лучей от пластины 3 и обратно к ней я задал маленькую скорость света в вакууме Vs0=30000 м/с и большую скорость установки Viso=6000 м/с, которая движется под углом Alfa(Viso)=90 градусов, т.е. вверх от источника света 5, как это принято на рис. 1b, а статические углы наклона зеркал я задал Alfa1=90 и Alfa2=0 градусов. Основной шаг решения системы уравнений, описывающих функционирование данной системы, я задал 10^-8 с, т.е. за один шаг лучи света смещаются в абсолютной системе отсчета (АСО), т.е. в неподвижном эфире, на 0,046 длины волны, которая задана L1=0,0065 м, т.е. 6,5 мм. А в те моменты, когда центры лучей подходят близко к поверхностям элементов установки, то для повышения точности решения основной шаг решения уменьшается в 1000 раз. И таким образом погрешность численного решения здесь будет 0,000046* L1. А на рисунке мы даже в масштабе 0,1 м/см видим, что вертикальный луч, возвращаясь к полупрозрачной пластине, не падает на нее в ту же точку откуда он вылетел.

Объясняется это тем, что двигаясь в компенсационной пластине 4, где произошло преломление луча, он двигался под углом Alfa23=70,04 градусов дольше, чем при движении в ней под углом Alfa26=255,47 градусов, когда возвращался отраженный от зеркала 2, т.к. при движении луча вверх он догонял пластину 4, а при движении вниз пластина двигалась ему навстречу. Таким образом, теория этого эксперимента, созданная Майкельсоном, уже только из-за этого не может быть применена для интерпретации результатов натурных экспериментов, а наличие в установке стекол только усложняет теоретические расчеты, не давая никаких положительных эффектов, т.е. позволяющих выявить абсолютную скорость Земли. Ну, и, естественно, мы только от учета эффектов отмеченных галочками на рис. 10, т.е. без учета эффекта Доплера, получаем смещение полос совсем не такое, как предполагалось в теории Майкельсона. Согласно данным нашего вычислительного эксперимента у нас будет время движения 1-го, т.е. горизонтального луча, от лазера до экрана T1=1,0517* 10^-4 с и 2-го, т.е. вертикального луча, T2=1,0656* 10^-4 с (см. на скриншоте в окошках Т1 и Т2), т.е. T1 - T2= -1,38* 10^-6 с, а разность фаз двух лучей рассчитанная по полному времени их движения, которое заложено Майкельсоном в основу теории этого эксперимента, будет dN1=v01*(T1 - T2)= -6,39 периодов.

И, если мы после выполнения этого вычислительного эксперимента нажмем в программе Maikelson1 на кнопку <Расчет Майкельсона>, то мы увидим этот наш расчет для всего пути и расчет по теории Майкельсона, где вычисляется только время движения лучей от момента касания общим лучом верхней стороны полупрозрачной стеклянной пластины 3 до моментов времени, когда два луча, разделившись в этой точке, долетят до горизонтального 1 и вертикального 2 зеркал и отразившись опять вернутся в эту точку на пластине 3. Так вот, по теории Майкельсона для части пути получается T1=6,936* 10^-5 с и T2=6,802* 10^-5, т.е. T1 - T2= +1,33* 10^-6 с, а разность фаз двух лучей dN2=v01*(T1 - T2)= +6,16 периодов. А, если мы теперь, перед тем как нажать на кнопку <Расчет Майкельсона>, отметим чекбокс <+ сравнительный расчет>, то мы увидим тот же расчет для части пути по теории Майкельсона dN2= +6,16 периодов и этот же расчет для части пути по данным вычислительного эксперимента dN3= - 13,15 периода. Таким образом, мы видим, что теория эксперимента созданная Майкельсоном дает абсолютно не правильный результат по смещению полос. И при движении установки в горизонтальной плоскости у нас тоже в вычислительных экспериментах будут получаться результаты отличающиеся от того, что дает теория Майкельсона. А для наглядности того, что пути движения лучей будут отличаться от того, что заложено в теории Майкельсона, я привожу на рис. 11 скриншоты программы с изображением траекторий движения двух лучей и при движении установки в горизонтальном направлении.

При этом, обращаю ваше внимание на то, что в вычислительном эксперименте на рис. 10 мы получили углы движения двух лучей на 8-м участке пути, т.е. при движении к экрану, для 1-го луча Alfa18= 12,68 и для 2-го луча Alfa28= 10,39 градусов, т.е. оба угла одного знака, а это значит, что у нас будут не обычные полосы, расчеты для которых производил Майкельсон, а составные полосы (см. правый рис. 12). А вот на рис. 11 мы видим, что при движении установки вдоль оси Х у нас будут обычные полосы на интерференционной картинке, т.к. здесь два луча имеют разные знаки углов движения и, следовательно, и углов падения на экран. Кстати и при движение установки вниз, т.е. при Alfa(Viso)=270 градусов, у нас тоже получатся углы движения лучей к экрану одного знака (для 1-го луча Alfa18= -10,39 и для 2-го луча Alfa28= -12,68 градусов), но теперь они будут отрицательные.

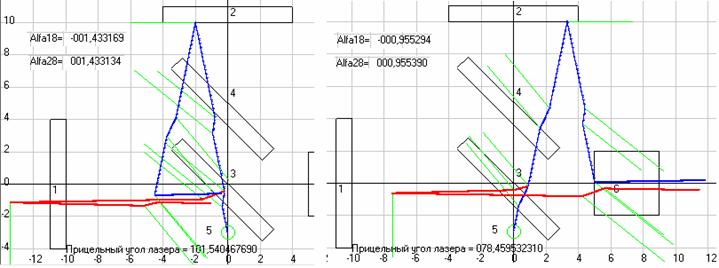
Рис. 11. Траектории движения двух лучей света от лазера до экрана в установке по схеме Майкельсона при ее движении горизонтально, где положение элементов установки показано в момент вылета лучей из лазера. Скриншоты программы Maikelson1, где на левом скриншоте установка движется влево Alfa(Viso)=180, а на правом скриншоте вправо Alfa(Viso)=0.

О том, что такое составные полосы, которые состоят из нескольких обычных полос, я расскажу далее подробно, т.к. в учебниках о них ничего не говорится и поэтому мне пришлось даже придумывать для них название. А здесь я только приведу два примера, когда углы падения лучей будут при повороте установки иметь или разные знаки углов падения лучей на экран или одинаковые. На рис. 12 слева мы видим обычные полосы, о которых говорят во всех учебниках, и здесь они у нас периодически то загораются, то гаснут в одних и тех же местах. Но изменение яркости будет происходить так быстро, что человеческий глаз этого не может заметить и мы будем постоянно видеть эти полосы светящимися. А на правом рисунке у нас эти отдельные полосы будут загораться и гаснуть не в одних и тех же местах, а постоянно смещаясь и мы должны были бы увидеть в тех участках экрана, где будут совпадать или минимумы или максимумы напряженностей двух лучей составные полосы, но мы их будем видеть как единое целое, т.к. визуально мы не сможем наблюдать отдельные полоски. При этом составные полосы будут постоянно смещаться в какую то сторону, а в нашем примере будут смещаться влево вместе с красной синусоидой.

Рис. 12. Варианты интерференционных полос, которые могут наблюдаться. Слева обычные полосы при разных знаках углов падения лучей на экран A1p= -5 и A2p= +5 градусов. Справа составные полосы, которые образуются из нескольких обычных полос при одинаковых знаках углов падения лучей на экран или при большой разности углов падения A1p= +1 и A2p= +21 градусов. Внизу показаны синусоиды изменения напряженности поля двух лучей, которые как бы движутся или навстречу друг другу (слева) или в одну сторону (справа), где на левом рисунке показан момент времени, когда полосы имеют максимальную яркость, т.е. амплитуды синусоиды 1-го луча (красная кривая) совпали с амплитудами синусоиды 2-го луча (синяя кривая). Скриншоты программы Maikelson1.

Но, т.к. до недавнего времени авторы этих экспериментов не использовали лазеры, т.е. и монохроматические и когерентные источники света, то может быть у них была и несколько иная интерференционная картинка, т.е. отличающаяся от той, что я описываю для лазерных источников света. Вот только ни кто из тех, кто проводил натурные эксперименты, не сообщал какие у них были углы наклона зеркал, т.к. их просто не возможно было измерить практически. Только Миллер написал, что у него углы наклона зеркал изменялись от 0 до 4 угловых секунд, т.е. от 0 до 0,0011 градуса, но я не понимаю как он это определил, т.к. он сам же пишет, что изменял угол наклона зеркал регулировочными винтами, которые за один оборот поворачивали зеркало аж на 0,36 градуса. И это касается только изменения относительных углов, а каково было абсолютное значение углов наклона зеркал он тем более не мог знать. А не зная этих углов мы не можем не только определить в какую сторону и на сколько должны смещаться полосы при повороте интерферометра, но не можем определить и ширину полос и даже их вид (обычные или составные).

Таким образом, интерферометр собранный по схеме Майкельсона совершенно не пригоден для проведения научных исследований, где мы должны не гадать на кофейной гуще, а четко знать на сколько полос и в какую сторону должны они смещаться при различных условиях проведения эксперимента. Поэтому я сейчас даже не буду касаться влияния эффекта Доплера на результаты этих экспериментов, хотя в программе у меня предусмотрен и учет этого эффекта при проведении вычислительного эксперимента на математической модели интерферометра Майкельсона (для этого надо перед началом вычислительного эксперимента отметить чекбокс <+ эффект Доплера>). Не буду я сейчас касаться и теории интерференции, которая дает смещение полос даже при одинаковом времени движения лучей, но когда они падают в разные точки на поверхности экрана, как мы это видим на рис. 10 и 11, (только этот эффект не имеет никакого отношения к объяснению на правом рис. 3, хотя небольшое смещение полос при разнице ординат точек падения на экран действительно должно быть), а сразу перейду к описанию интерферометра своей конструкции, который позволяет проводить на нем именно научные исследования, а не играться, как детишки, разглядывая картинки на интерферометре Майкельсона.

3. Математическая модель установки Юдина

При создание своего интерферометра я первым делом решил исключить из него стекла, чтобы лучи весь путь от лазера до экрана двигались только в воздухе. Поэтому для разделения луча от лазера на два отдельных когерентных луча я применил стеклянную треугольную призму, как это изображено на рис. 13, а зеркала использовал металлические, чтобы не было двойного отражения света, как это будет у стеклянных зеркал с посеребренной задней стороной. Если призма установлена так, как изображено на схеме a), то луч лазера 5, упав на ребро призмы 3, разделится на два луча, которые, отразившись от боковых поверхностей призмы, полетят один к зеркалу 1, а второй к зеркалу 2 и отразившись от зеркал полетят к экрану 6. А, если призма установлена так, как изображено на схеме c), то луч от лазера тоже разделится на два луча, но левый луч так и продолжит лететь в направление экрана, а правый луч полетит к экрану отразившись от зеркала 2. Но, если мы в схеме c) на пути первого луча, пролетающего мимо призмы, установим зеркало 4, то он отразится от него и полетит вправо, как это изображено на схеме b). И теперь, если мы установим на его пути еще и зеркало 1, то он отразившись от него полетит к экрану и упадет на него с той же стороны, что и второй луч. К сожалению практика показала, что в схемах b) и c) трудно выставить призму так, чтобы левый луч пролетал строго параллельно грани призмы, поэтому я при дальнейших исследованиях возможно, что поверну призму так, чтобы левая часть луча, падающего на призму, отражалась к правому зеркалу, а правая часть пролетала мимо ребра призмы.

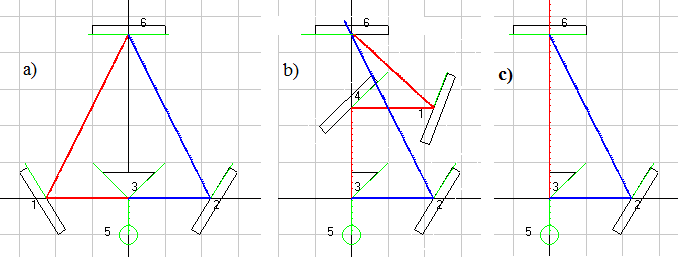
Рис. 13. Схемы движения лучей в установке Юдина для падения лучей на экран с разных сторон (схема a)), когда будут наблюдаться обычные полосы, с одной стороны (схема b)), когда будут наблюдаться составные полосы, и вариант, когда один луч падает перпендикулярно плоскости экрана (схема c)), когда будут тоже наблюдаться обычные полосы.

Преимуществом данной конструкции интерферометра является не столько то, что мы избавились от стеклянных пластин, сколько то, что теперь мы можем точно при проведении натурных экспериментов задавать углы наклона зеркал. Это позволяет нам и определить вид наблюдаемых при интерференции полос и рассчитать теоретически их ширину, а также предсказать на сколько и в какую сторону они должны смещаться. К достоинствам данной конструкции следует отнести и то, что вследствие больших углов падения лучей на экран интерференционная картинка получается более устойчивой к различным деформациям элементов установки. А в интерферометре Майкельсона, где углы падения лучей просто микроскопические, малейшие деформации приводят к очень заметным изменениям интерференционной картинки. Да, при больших углах падения лучей на экран у нас получается ширина полос значительно меньше, чем в установке Майкельсона, поэтому требуется или мощная оптика, чтобы увидеть эти полосы, или использование фото или видео приборов с матрицей высокого разрешения. При этом, как я уже писал выше, различная оптика вообще-то тут не желательна, и поэтому я использую вэбкамеры из которых удаляю оптику.

И на рис. 14 вы видите общий вид моего интерферометра, где изображение с вэбкамеры транслируется на экране ноутбука. При этом, как вы видите, я все таки перед вэбкамерой поместил и оптику, а конкретно объектив от кинопроектора Луч-2, т.к. разрешение матриц моих вэбкамер не очень высокое. Одна вэбкамера, которая дает изображение 640*480 писелей, имеет разрешение 2,2 мкм на пиксель, а другая вэбкамера, которая дает изображение 1920*1080 писелей, имеет разрешение 3 мкм на пиксель. А объектив кинопроектора дает мне увеличение в 48 раз на каждый метр расстояния между ним и вэбкамерой, что позволяет мне уверенно наблюдать даже самые узкие полосы. Но во многих экспериментах я обхожусь и без объектива кинопроектора, направляя лучи от зеркал сразу на матрицу вэбкамеры. При этом, чем дальше находится вэбкамера от зеркал, то при том же расстоянии от треугольной призмы до зеркал, у нас получаются более широкие полосы, т.к. при этом уменьшаются углы падения лучей на экран. Как видно на рисунке, кабель от вэбкамер идет на подвеску, на которой может поворачиваться установка, и при ее вращении кабель делает несколько оборотов вокруг нити подвески, что позволяет избавиться от необходимости передачи сигнала от вэбкамеры через дополнительные электронные устройства на ноутбук расположенный за пределами установки.

Рис. 14. Фотография общего вида установки моей конструкции интерферометра собранного по схеме а) на рис. 13. Установка ориентирована при движение лучей с юга (от лазера) на север (к вэбкамере).

При создании математической модели своей установки я использовал те же физические эффекты, которые рассмотрел при описании математической модели установки Майкельсона за исключением только явления преломления луча света при переходе из среды с одной оптической плотностью в среду с другой оптической плотностью, т.к. у меня тут нет стекол. Но я добавил в свою модель и некоторые варианты учета различных эффектов, таких как, например, эффекта изменения угла наклона движущихся зеркал, где возможны варианты его расчета не только численными методами, но и по аналитическим зависимостям (моим и Хедрика). И точно также в моей модели имеется не только возможность смоделировать эффект Доплера, как в модели Майкельсона, рассматривая движение двух фронтов волн, как это было при рассмотрении движения фронта волны для определения эффективного угла наклона зеркал, но и рассчитать его аналитически (причем в двух вариантах или с использованием статических углов наклона зеркал или динамических). При этом можно изменять количество периодов N0 для моделирования этого эффекта, выводить анимацию этого процесса на экран как с движением только двух фронтов волн отстоящих друг от друга по времени движения на N0 периодов колебаний света, так и с отображением траекторий движения краев этих двух фронтов.

Но самое большое отличие моей модели от модели Майкельсона заключается в моделировании еще и сплошного эффекта Доплера, когда два фронта, вылетевших из лазера, движутся непрерывно до самого экрана, а их направления движения при отражении уже определены при выполнении основного вычислительного эксперимента. Так вот, в модели Майкельсона при этом определяется только частота света принятая различными поверхностями (призмы, зеркал и экрана), а в моей модели определяется и частота света на пути от одной поверхности до другой. Это связано с тем, что эффект Доплера оказалось не так просто определить, если речь идет о многократном переотражение волн от движущихся поверхностей и поэтому на этом эффекте я остановлюсь далее очень подробно при обсуждении экспериментов на моей установке. А сейчас только добавлю, что в моей модели есть два варианта учета влияния плотности оптической среды на параметры самого луча света, т.е. на его скорость и частоту. Что касается уменьшения скорости света в более плотных оптических средах при неизменной частоте, то это считается общеизвестным фактом, но я предусмотрел и вариант расчета когда в более плотных средах уменьшается частота света при неизменной его скорости, что приводит к такому же уменьшению длины волны, как и при уменьшении скорости света. И, хотя это чисто гипотетический эффект, экспериментального подтверждения которому я не встречал в научной литературе, но я решил рассмотреть и его, т.к. в эксперименте с изменением давления воздуха цилиндре, расположенном на пути 2-го луча, именно этот эффект позволяет наиболее просто объяснить смещение полос при одном из вариантов расчета начальных фаз двух лучей при интерференции.

К достоинствам моей схемы установки следует отнести и то, что она позволяет грамотно ее настроить, а не просто крутить туда и сюда зеркала пока не появятся какие ни будь полосы, как делается в установке Майкельсона. Ведь в установке Майкельсона все время сравнивается движение двух лучей в системе движущейся со скоростью Земли при одном положении установки и при повороте ее на 90 градусов, но никак не говориться, а как же настраивалась установка для одинакового времени прихода лучей к экрану. Ведь прежде, чем начинать измерения, надо быть уверенными в том, что зеркала выставлены так, что в покоящейся системе обеспечивают одинаковое время прихода лучей к объективу зрительной трубы. Но этого мы не можем сделать в принципе на установках собранных по схеме Майкельсона, а вот моя установка позволяет это сделать, т.к. при движение установки вверх и вниз лучи пересекаются на приемнике (экране) в одной и той же точке в середине экрана, а при движение вправо или влево смещаются симметрично относительно середины экрана. Это позволяет даже без измерения углов абсолютно точно устанавливать зеркала под одним и тем же углом, а то, что мы при этом не сможем или не захотим очень точно измерить их абсолютные значения не влияет заметным образом на результаты расчетов. В то время, как мы это видели для установки Майкельсона, ошибка в абсолютных значениях углов наклона зеркал приводит к очень заметным расхождениям в получающихся результатах и при этом измерить точно эти маленькие углы очень проблематично.

4. Теория интерференции

К сожалению, говоря об эксперименте Майкельсона-Морли или о подобных ему экспериментах, например, об эксперименте Физо, все обсуждают только теорию этих экспериментов, но ни кто не касается теории интерференции, а там пока неясных вопросов тоже предостаточно. К тому же изложена она в учебниках так бестолково, что я буду ее излагать вместе с теми ошибками, которые я совершал, разбираясь в ней. Сейчас считается, что освещенность какой то поверхности, т.е. интенсивность света на этой поверхности I зависит от квадрата амплитуды напряженности электрического поля световой волны E, падающей на эту поверхность. Но во всех учебниках пишут только то, что I пропорциональна E^2, а как она конкретно зависит от параметров светового луча ни где не говориться. Только авторы учебника [13, стр. 82] пишут "Электромагнитное поле волны определяется обоими векторами E и H. Поэтому выбор вектора E, а не H, сделанный выше при формулировании условия интерференции когерентных волн, нуждается в специальном обосновании. Для решения этого вопроса необходимо выяснить, какой из векторов (E или H) определяет действие на органы зрения, фотопластинки, фотоэлементы и другие приборы ...". И далее, они, рассматривая электронную теорию, пишут, "... действие света на электроны вещества в основном определяется электрическим вектором E электромагнитного поля."

А здесь, даже рассматривая воздействие света только на электроны, они пишут, что это действие света определяется в основном вектором E. Но давайте не будем углубляться в эти тонкости и просто согласимся с утверждением, что интенсивность света I пропорциональна E^2 . При этом, если рассматривается интенсивность света в конкретной точке поверхности, куда падают два некогерентных луча света, считается, что эта суммарная интенсивность будет определяться по формуле (1-1), а напряженности электрического поля двух лучей одинаковой мощности, т.е. с одинаковой максимальной амплитудой колебания напряженности E0, будут определятся по формулам (2). Здесь у нас Q1 и Q2 начальные фазы колебаний света двух лучей в один и тот же момент времени их падения на экран t=0, а w1 и w2 это круговая (циклическая) частота колебаний света.

I= I1 + I2= E1^2 + E2^2 (1-1)

E1=E0*cos(w1*t + Q1)

E2=E0*cos(w2*t + Q2) (2)

Действительно, если исходить из того, что интенсивность света это мощность светового потока, падающего на конкретную площадь поверхности, то все выглядит логично, т.к. две мощности должны просто арифметически суммироваться. Хотя, как мы это видели, анализируя в статье [12], посвященной эффекту Доплера, эксперименты германских ученых с двойным оптическим резонансом, здесь пока еще очень много не ясных вопросов. Ведь у них мощность излучения ионов лития от воздействия на них двух лазеров не увеличивалась в этих экспериментах линейно от суммарной мощности лазеров. Но, давайте будем считать, что у нас при интерференции двух лучей будет линейная зависимость суммарной освещенности от суммы освещенностей двух лучей. При этом, т.к. частота света очень большая, то расстояния между точками на поверхности экрана, куда падают фронты световых волн разной фазы, будут очень маленькие и глаз не заметит, что освещенность в разных точках экрана постоянно меняется. К тому же и время в течение которого глаз способен зафиксировать изменения освещенности очень большое (примерно 0,1 с и мы не замечаем моргания лампочки накаливания даже с частотой 50 Гц) поэтому мы будем видеть равномерно освещенную поверхность. А, если учесть, что две световые волны с разными частотами, т.е. некогерентные, будут изменять общую освещенность в каждой точке экрана со случайной периодичностью, то мы будем видеть, что при падении на экран двух лучей одинаковой интенсивности, общая (средняя) интенсивность света увеличилась в два раза.

Но, если мы рассматриваем случай, когда у нас два когерентных луча света падают на экран, то здесь возникает некоторая периодичность в освещенности различных участков экрана и мы видим интерференционные полосы (если волны света плоские). В тех точках, где максимальные значения интенсивности света обоих лучей будут совпадать, мы увидим светлые участки, а там где совпадут минимальные освещенности мы увидим темные участки. И вот здесь начинается самое интересное, хотя у наших двух лучей одинаковой интенсивности их напряженности электрического поля в конкретной точке экрана будут изменятся точно так же по формулам (2). Если исходить из того, что у нас просто будут суммироваться мощности двух волн в конкретных точках экрана, то можно было бы воспользоваться формулой (1) для суммирования интенсивностей двух лучей и в этом случае, т.е. когда у нас два луча когерентны. Но сегодняшняя теория интерференции гласит, что в этом случае суммарную освещенность надо считать не по формуле (1-1) а по другому и нам предлагают сначала вычислять суммарную амплитуду колебания напряженности электрического поля, а потом уже вычислять суммарную интенсивность света по этой суммарной амплитуде.

Для этого нам предлагают воспользоваться векторной диаграммой сложения амплитуд двух гармонических колебаний действующих в одном направлении, но при разных фазах. Но такое сложение амплитуд двух гармонических колебаний вообще то предполагает наличие объекта, который и совершает эти колебания, например, масса на пружине. Поэтому, например, мне не понятно почему надо делать именно так как будто бы у нас есть какой то элемент, который аккумулирует в себе две амплитуды от внешних воздействий, если не считать, что за такие объекты принимаются электроны материала экрана. Но давайте опять не буде спорить и применим для этого формулу вычисления суммарной амплитуды, а потом уже вычислим интенсивность света по этой суммарной амплитуде Ee полученной по формуле (1-2), где Q2 и Q1 это фазы амплитуды напряженности двух лучей для конкретных точек экрана. Но авторам многих учебников не нравиться и эта формула (1-2) поэтому они, как профессиональные фокусники, ничего не объясняя, достают из рукава формулу (1-3), которую, чаще всего записывают как (1-3') и говорят, что вот именно этой формулой и надо пользоваться при объяснении явления интерференции.

I= Ee^2= (E1 + E2)^2= E1^2 + E2^2 + 2*E1*E2*cos(Q2-Q1) (1-2)

I= E1^2 + E2^2 + 2*sqrt(E1^2*E2^2)*cos(Q2-Q1) (1-3)

I= I1 + I2 + 2*sqrt(I1*I2)*cos(Q2-Q1) (1-3')

Но, например, в Википедии [17], авторы статей в которой должны обобщать все теории, изложенные во всех учебниках, они приводят только формулу (1-2). Хотя тут надо заметить, что я не обратил внимания на то, что там вместо E1 и E2 использованы значения E10 и E20, а это, как будет показано далее, является принципиальным. Ведь у них рассматривается преобразование комплексных амплитуд, а с их использованием получается формула (1-2), где вместо текущей напряженности Е надо использовать амплитуды напряженности Е0. Но потом многие авторы учебников без всяких пояснений, например, Сивухин [18], резко заявляют, что, вводя интенсивности колебаний, этот результат можно записать как (1-3'). А в некоторых учебниках вообще стараются не касаться вывода формулы (1-3) и, например, Иродов [16] ухитрился на одной страничке изложить весь вывод формулы (1-3), а конкретно он сразу записывает уравнение (1-2) и тут же пишет, что его надо использовать как (1-3').

И, наверное, вот тут, сосредоточив свое внимание именно на этом некорректном с моей "механической" точки зрения переходе от уравнения (1-2) к (1-3), я и упустил из вида, что во всех этих уравнениях используются именно амплитуды напряженностей. К тому же формула (1-3) давала хорошую картинку интерференционных полос и при использовании мною в ней текущих напряженностей, т.е. с учетом фаз двух лучей, и поэтому у меня и не возникло сомнений в правильности использования мною в этой формуле текущих напряженностей. И потом, я даже предположить не мог, что в этих формулах используется амплитуда напряженности, т.к. в этом случае мы получаем чисто геометрическую интерпретацию этого явления. Ведь у нас получается статическая картинка и подсчет энергии освещенности полос, рассчитанной по этой формуле, ведет к явному нарушению закона сохранения энергии. Ну и, конечно же, некоторое недоверие к правильности вывода формул (1-2) и (1-3) вызвало у меня и то, что, например, авторы учебников [14, 15, 18] тоже нашли "парадокс" нарушения закона сохранения энергии в ими же рекомендуемой формуле (1-3). Но при этом они пишут, что, только если расстояние между щелями в опыте Юнга будет меньше половины длины волны, то у них получается, что в этом случае на экране не будет темных полос и поэтому энергия двух лучей получится гораздо больше исходной энергии. И здесь интересно то, что заявленного ими парадокса не будет, если смоделировать этот вариант с использованием формулы (1-3) в моей интерпретации (что, как будет показано далее, вполне допустимо), т.к. я при этом получил точно такие же полосы, как и при другом расстоянии между щелями.

Но самое интересное здесь то как эти математико-физики объясняли заявленный ими же энергетический "парадокс". Так Ландсберг [14, стр. 82] пишет "Здесь, конечно, нет никакого нарушения закона сохранения энергии. Мы имеем дело с действительным увеличением энергии, используемой за единицу времени парой когерентных источников благодаря воздействию их друг на друга. Энергия эта доставляется из тех запасов, которые питают наши источники". Ему вторит и Матвеев [15, стр. 170], который пишет "... при расстоянии λ / 2 между двумя источниками излучения мощность их совместного излучения не равна сумме мощностей излучения этих источников в отдельности. ... Различие в энергии полей полностью объясняется изменением мощности излучателей. Например, если полная интенсивность увеличивается в результате интерференции, то мощность взаимодействующих между собой через поле излучателей должна увеличиваться". Я думаю, что только из этих двух цитат сразу становится ясно, каким местом думают современные математико-физики, когда у них лампочка включенная в розетку и луч от которой делится на два, при интерференции этих двух лучей начинает потреблять не только постоянное значение энергии из розетки, но она еще и через волшебное взаимодействие сама с собою начинает черпать энергию из "закромов родины".

И все это при том, что сам же Ландсберг [14, стр. 81] пишет "Максимумы и минимумы освещенности, наблюдаемые в интерференционных картинах, не связаны, вообще говоря, с какими либо превращениями лучистой энергии...". А вот как интересно Матвеев [15, стр. 151] объясняет наличие темных полос на экране - "Это означает, что никакого потока энергии в направлении экрана D от пластины O нет, т.е. весь поток лучистой энергии возвращается в направлении источника S0". Я думаю, что после таких заявлений по описанию физических процессов протекающих при явлении интерференции, у любого нормального читателя возникнут сомнения в правильности вывода математико-физиками формул (1-1), (1-2) и (1-3), а поэтому и у меня не было никакой уверенности, что хоть одна из этих формул правильная. Более того, опережая события скажу, что все эти формулы не правильные, даже, если в них использовать амплитуду напряженности поля, т.е. вместо E1 и E2 использовать значения E10 и E20, как это должно быть по мнению авторов учебников. И при этом применение формулы (1-3) с использованием в ней напряженности поля рассчитанной по формулам (2), как это делал я, дает гораздо более правильные результаты. Поэтому давайте сначала посмотрим, что нам могут дать эти три формулы (1-1), (1-2) и (1-3), при расчете интенсивности света в них по формуле (2), но не в одной точке на экране, а на всей ширине экрана.

Для этого давайте рассмотрим падение двух фронтов плоских волн на экран в разных его точках и под разными углами, как это отражено на рис. 15. В данный момент времени t=0 центр 1-го фронта, движущегося под углом А1 со скоростью V1, упал на экран в точке с координатой Х1, а центр 2-го фронта, движущегося под углом А2 со скоростью V2, упал на экран в точке с координатой Х2. И в данный момент времени у нас начальные фазы напряженности электрического поля в лучах будут, соответственно, Q1 и Q2. Но нам надо рассчитать какие будут фазы у этих лучей, когда их фронты волн упадут в произвольную точку экрана, а для этого нам надо вычислить скорость с которой будет распространяться фиктивная точка пересечения фронтами волн оси абсцисс. Я по аналогии со скоростью перемещения солнечного зайчика при изменении угла наклона зеркала, посылающего солнечный зайчик на экран, назвал скорость перемещения этой фиктивной точки скоростью зайчика напряженности, которая определится по формуле (3). При этом обращаю ваше внимание на то, что и координаты падения двух лучей на экран и углы скоростей и сами скорости лучей, которые у нас получатся при моделировании работы интерферометра в АСО, надо будет перед тем, как производить расчет интерференционной картинки, перевести в ИСО экрана.

Ve= Vs / cos (A) (3)

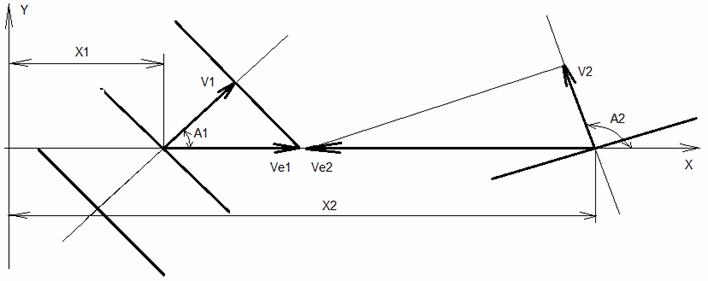
Рис. 15. Падение двух фронтов плоских волн на экран, расположенный горизонтально.

Таким образом, например, фронт 1-го луча, двигаясь по экрану от точки с координатой Х1 со скоростью Ve1, достигнет точки с произвольной координатой Х за время dt1=(X-X1) / Ve1, а фронт 2-го луча, двигаясь по экрану от точки с координатой Х2 со скоростью Ve2, достигнет точки с произвольной координатой Х за время dt2=(X-X2) / Ve2. Как нетрудно заметить, скорость зайчика 1-го луча в нашем случае будет положительной, а скорость зайчика 2-го луча отрицательной и поэтому во всех точках, которые фронты лучей достигнут, двигаясь в направлении скорости своих зайчиков напряженности, фазы напряженности в лучах будут больше их начальных фаз Q1 и Q2, которые были в момент времени t=0, когда центры фронтов коснулись поверхности экрана. При этом, естественно, что фазы напряженности в точках расположенных левее Х1 для первого луча и правее Х2 для второго луча будут меньше начальных фаз, т.к. зайчики напряженности уже прошлись по этим участкам экрана до момента времени t=0. И теперь начальные фазы напряженности для произвольных точек экрана выразятся зависимостями (4-1), где w1 и w1 это круговая частота света двух лучей, а Q1 и Q2 это начальные фазы напряженности в лучах в точках их падения на экран в один и тот же момент времени.

Q31= Q1 + w1*dt

Q32= Q2 + w2*dt2 (4-1)

При этом обращаю ваше особое внимание на то, что здесь Q1 и Q2 это не фазы в лучах света в моменты времени T1 и T2, когда они достигли экрана в установке Майкельсона, а фазы этих лучей для одного и того же произвольного момента времени когда центры двух лучей одновременно коснулись плоскости экрана. На этом вопросе определения начальных фаз двух лучей для расчета интерференционной картинки я очень подробно остановлюсь далее, а сейчас давайте посмотрим какая конкретно у нас будет получаться интерференционная картина с использованием различных формул для двух лучей в тестовом примере, который я рассмотрел в своей статье [12] (в 4-ой редакции), где я для расчетов использовал программу Dopler5. В этой статье я рассмотрел расчет с использованием всех трех формул (1-1), (1-2) и (1-3) для случая, когда у нас напряженность поля в этих формулах определяется по формуле (2), но не с фазами Q1 и Q2, т.е. для точки на экране, куда упали центры лучей, а для произвольных точек на экране, где в этих формулах (2) вместо Q1 и Q2 надо использовать фазы Q31 и Q32 рассчитанные по формуле (4-1). В этих расчетах я принимал в тестовом примере длину волны света в лучах L= 0,002 м и скорость света Vs= 20 м/с. При этом я рассматривал там вертикальное положение экрана, т.е. как в установке Майкельсона, где два луча падают на него слева точно в центр экрана, т.е. в точку с координатами Y1= Y2= 0 и под одинаковыми углами, но с разными знаками, т.е. A1= 1 градус и A2= -1 градус и при этом углы падения лучей тоже будут 1 и -1 градус.

Рис. 16. Изменение освещенности экрана при падение на него двух когерентных лучей при расчете освещенности экрана по формуле (1-1). На левом рисунке когда интенсивность света рассчитывается так же, как и в формулах (1-2) и (1-3), т.е. I=E^2, а на правом по ее удвоенному значению, когда I=2*E^2. На обоих рисунках вверху и внизу максимальная яркость светлых полосок, а на среднем минимальная. Скриншот программы Dopler5. Воспроизведено из работы [12].

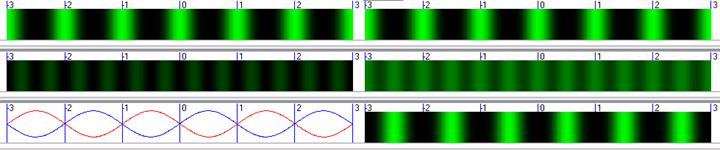
Рис. 17. Изменение освещенности экрана при падение на него двух когерентных лучей. На левом рисунке при расчете по формуле (1-3), а на правом по формуле (1-2). На левом рисунке - вверху максимальная яркость светлых полосок, а на среднем минимальная и на нижнем изменение амплитуды напряженности двух волн при минимальной яркости полос. А на правом рисунке - вверху и внизу максимальная яркость светлых полосок в двух разных положениях на экране, а на среднем рисунке минимальная яркость светлых полосок. Скриншот программы Dopler5. Воспроизведено из работы [12].

Как видим, все формулы (1-1), (1-2) и (1-3) с напряженностью рассчитанной по формулам (2) дают нам интерференционные картинки, которые отличаются только деталями. При этом светлые полоски периодически то появляются, то исчезают с очень большой частотой и поэтому глаз их видит постоянно как не моргающие. Но максимальная яркость полосок, т.е. их освещенность или интенсивность света в них, при расчете по формуле (1-1) получается в два раза меньше, чем по формулам (1-2) и (1-3). Поэтому навряд ли мы сможем их наблюдать визуально. А, если ее уровнять с яркостями последних, т.е. увеличить в два раза, как это дано на правом рис. 16, то у нас получается, что при максимальной яркости светлые полоски, которые будут возникать при совпадении полупериодов изменения напряженности электрического поля двух лучей (соответственно, верхняя и нижняя картинки), практически будут перекрываться, т.е. у нас при визуальном восприятии полосок будет засвечен весь экран и мы не увидим никаких полос. Поэтому формула (1-1) не подходит для построения интерференционной картинки, которую наблюдали в натурных экспериментах.

А вот при использовании формулы (1-2), которая, как и формула (1-1), тоже периодические дает светлые полоски в двух разных местах на экране, т.е. при совпадении полупериодов изменения напряженности электрического поля, а не периодов, как получается по формуле (1-3), полного перекрытия светлых полосок при визуальном восприятии все же не будет. Между ними все таки будет оставаться, хоть и очень тонкая, но все таки темная полоска, т.к. ширина именно светлой полоски будет такой же, как и при расчете по формуле (1-3), т.е. уже, чем при расчете по формуле (1-1). Вот только получающаяся с использованием формулы (1-2) ширина полос, т.е. видимое расстояние между двумя соседними светлыми или темными полосками, не соответствует их расчетному значению полученному ни по упрощенной формуле (5-1), которая приводиться почти во всех учебниках, т.к. выводится с упрощениями для малых углов падения лучей, когда синус угла примерно равен самому углу, ни по более точной формуле (5-2). Хотя и очень редко, но мне встречалась формула, где в знаменателе стоит еще двойка, а тогда значение ширины полос получается в два раза меньше, т.е. это значение будет соответствовать применению формул (1-1) и (1-2) с использованием в них текущих напряженностей, согласно формуле (2). В формулах (5-1) и (5-2) L0 это длина волны света и A1p и A2p это углы падения лучей на экран, а не углы скоростей A1 и A2, которые приведены на рис. 15. Поэтому для рассматриваемого нами примера на рис. 15, когда лучи падают на экран расположенный горизонтально с углами скоростей A1 и A2, углы падения лучей будут А1p=А1 - 90 и А2p=А2 - 90.

B= L0 / (A2p - A1p) (5-1)

B= L0 / (sin(A2p) - sin(A1p)) (5-2)

А вот если мы будем считать рассчитанную нами по формулам (1-1)...(1-3) интенсивность света просто мощностью светового потока на одном квадратном метре освещаемой поверхности и проинтегрируем эту мощность светового потока по всей поверхности экрана за конечный промежуток времени, то мы получим суммарную энергию освещенности всего экрана. Ведь интенсивность света или плотность светового потока, которую в оптике называют освещенностью или светимостью и которая измеряется в люксах, т.е. в люменах на квадратный метр, является аналогом энергетической светимости, которая измеряется в ватах на квадратный метр. Прямого пересчета электрических величин в оптические я не нашел, но между ними все же есть соотношение, т.к. принято, что один люмен равен силе света в одну свечу умноженной на телесный угол в один стерадиан и что одна свеча это сила света, создаваемая источником с длиной волны 555 нм и посылающим свет в одном направлении, которая при этом составляет 1/683 вата на телесный угол. Но у меня в этих трех вычислительных экспериментах результат будет получаться в каких то условных единицах, т.к. я буду задавать единичную ширину экрана и приму максимальную интенсивность света, рассчитанную по формулам (1-1)...(1-3), равной 255 условным единицам. В результате за 0,1 секунды мы получим, по заданным при расчете картинок на рис. 16 и 17 параметрам лучей, следующие значения световой энергии, рассчитанные по разным формулам при численном решении уравнений с шагом по времени 10^-7 с и с шагом суммирования по ширине экрана равном 1/550 его ширины.

E(1-1)=3513 усл. единиц

E(1-2)=5273 усл. единиц

E(1-3)=3519 усл. единиц

Таким образом, мы имеем прямое нарушение закона сохранения энергии с использованием формулы (1-2), т.к. энергия получается гораздо больше, чем это было в этих двух лучах согласно формуле (1-1), энергию излучения по которой мы принимаем за 100%. Более того, формула (1-2) мало пригодна для практических расчетов, т.к. у нас, как и при применение формулы (1-1) с двойной яркостью полос, получается, что будет засвечен практически весь экран и мы визуально не сможем увидеть отдельных светлых полосок. Следовательно, для практического использования остается только формула (1-3), которая при этом не только дает четкие полосы, которые мы сможем увидеть визуально, но она дает и правильное значение видимой ширины полос при встречном движении зайчиков напряженности двух лучей. Забегая вперед скажу, что я проверил в натурных экспериментах расчет по этой формуле видимой ширины полос и это расчетное значение совпало с наблюдаемым. Однако, как я заявил выше, оказывается и формула (1-3) является ошибочной, если в ней использовать текущие напряженности рассчитанные по формуле (2), хотя она и дает результаты, которыми можно пользоваться практически. А выяснилось это при обсуждении мною формул (1-2) и (1-3) на форуме SciTecLibrary [19], где Сергей Цикра написал, что во всех этих формулах E1 и E2 это не текущая напряженность поля в конкретной точке экрана, которая в точке падения лучей на экран изменяется по синусоидальной зависимости согласно формулам (2), а максимальное значение этой напряженности, т.е. это амплитуда напряженности E0.

I= Ee^2= (E1 + E2)^2= E1^2 + E2^2 + 2*E1*E2*cos(Q2-Q1) (1-2)

I= E1^2 + E2^2 + 2*sqrt(E1^2*E2^2)*cos(Q2-Q1) (1-3)

I= (E1 + E2)^2= E1^2 + E2^2 + 2*E1*E2 (1-4)

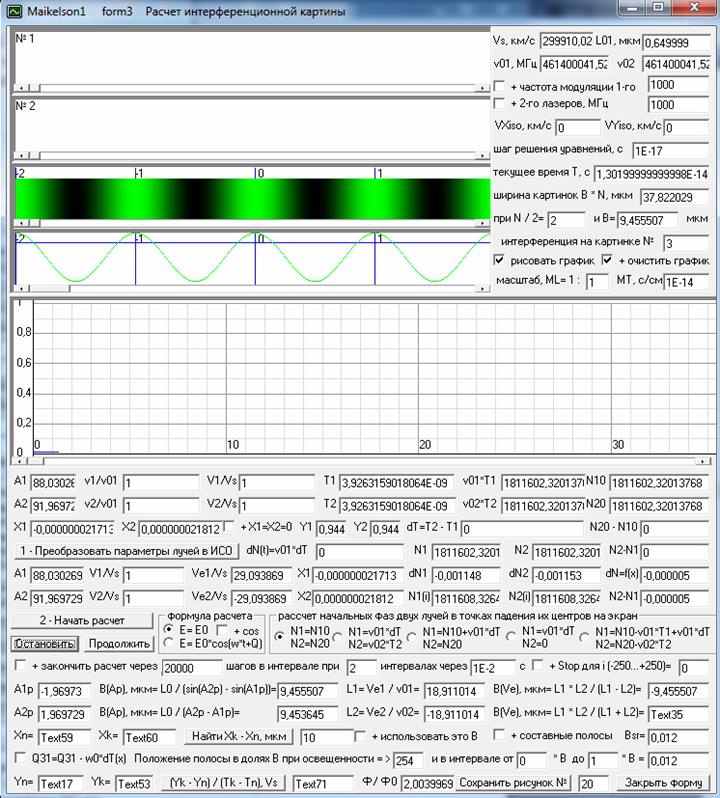
Рис. 18. Интерференционная картинка получающаяся при использовании в формул (1-2) и (1-3) максимальных значений напряженностей двух лучей, т.е. их амплитуд Е0 (включен переключатель <E=E0>). Интерференционная картинка построена по результатам вычислительного эксперимента повторяющего натурный эксперимент, где получена интерференционная картинка изображенная на левой фотографии рис. 19. Скриншот программы Maikelson1.

И, если мы в этих формулах (1-2) и (1-3) вместо E1 и E2 будем использовать амплитуду изменения этих напряженностей, т.е. значение E0, то обе формулы дадут одинаковый результат, т.к. теперь 2*E1*E2 будет равно 2*sqrt(E1^2*E2^2). А при использовании в этих формулах вместо Q1 и Q2 их значений для произвольной точки на экране Q31 и Q32 мы получим статическую интерференционную картинку с максимальной яркостью полос, как это отражено на рис.18, где суммарная напряженность в различных точках экрана (зеленая синусоида) не изменяется со временем. Но она изменяется в разных точках экрана, т.к., хотя напряженности в обоих лучах остаются неизменными (красная и синяя прямые, отражающие амплитуду напряженности, совпали), у нас изменяются конечные фазы напряженностей согласно формулам (4-1).

А далее Сергей Цикра пишет, что динамическая интерференционная картинка у нас получится, если мы будем использовать его формулу (1-4), где и надо использовать именно текущие значения напряженностей E1 и E2, рассчитанные по формуле (2), а не максимальные их значения, т.е. амплитуды, E0. Сейчас у меня в программе Maikelson1 нет расчета по формулам (1-1) и (1-2), которые я использовал при построении интерференционных картинок на рис. 16 и 17 с помощью программы Dopler5. Я в программе Maikelson1 оставил только два варианта расчета или по формуле (1-3) с использованием амплитуд напряженностей (для этого надо в рамке <формула расчета> включить переключатель <E= E0>) или по формуле (1-4) с использованием текущих напряженностей (для этого надо отметить переключатель <E= E0*cos(w*t+Q)>). А для сравнения результатов с теми, что я получил ранее в программе Dopler5 по формуле (1-3) с использованием текущих напряженностей, надо выбрать переключатель <E= E0*cos(w*t+Q)> и отметить чекбокс <+ cos>.

После этого я более внимательно вчитался в то, что пишут авторы учебников, и понял, что они рассматривают не реальную освещенность полос, а фиктивную освещенность по уравнению, которое позволяет производить с ним различные манипуляции для получения некоторых аналитических решений этого уравнения. Ведь в учебниках для суммирования амплитуд колебаний заданных формулами (2) вводятся комплексные амплитуды, а потом уже после их суммирования отделяется вещественная часть амплитуды от мнимой и получаются выражения (1-2) или (1-3), которые в данном случае будут идентичны, т.к. вместо E1 и E2 в них будет E0. Да, с математической точки зрения, наверное, все это сделано корректно, но ведь кроме умения делить и умножать надо еще хоть немного и думать. А здесь у математико-физиков получилась интерференционная картинка, которая не меняется со временем и поэтому нарушается закон сохранения энергии. Более того, например, авторы учебника [13, стр. 25] пишут "б) разность фаз Q2-Q1 не зависит от времени; такие волны и возбуждающие их источники называются когерентными", т.е., переводя этого на русский язык, они заявляют, что, когда нарушается закон сохранения энергии, то, следовательно, у нас имеются когерентные источники света. И для объяснения этого вывода они тоже начинают фантазировать на вольные темы, как мы это видели в цитатах из работ [14, 15], которые я приводил выше. Например, в учебнике Сивухина [19, стр. 196] мы опять видим это нарушение закона сохранения энергии и новые фантазии, позволяющие доказать нам, что на самом деле никакого нарушения закона сохранения энергии нет а "закромами родины", откуда черпается дармовая энергия, у него в объяснениях является волшебный генератор. Конкретно он пишет

"... Когда же d<< λ, то во всех точках пространства складываются колебания, фазы которых практически одинаковы. В этом случае интенсивность результирующего колебания, а с ним и поток результирующего излучения, исходящий от обоих источников, в четыре раза больше соответствующих величин для одного из источников в отсутствие другого. Таким образом, если расстояние между источниками S1 и S2 меньше длины волны λ, то поток лучистой энергии через замкнутую поверхность, окружающую эти источники, больше суммы потоков, которые излучали бы те же, но уединенные источники.

Однако принцип сохранения энергии и не требует равенства этих величин. Источники вместе действительно больше излучают энергии, чем в том случае, когда они находятся далеко друг от друга. Но это увеличение излучения происходит не за счет нарушения сохранения энергии, а за счет работы генератора, который должен поддерживать постоянными амплитуды колебаний в источниках. Если же колебания в источниках свободные, то увеличение излучения приводит просто к более быстрому затуханию этих колебаний."

А теперь посмотрите на рис.18 в текстовое окошко <Ф / Ф0> (это в самом низу). Здесь у меня выводится отношение суммы по всему экрану результирующего излучения, т.е. светимости полос, при интерференции, когда эта светимость рассчитана по формулам (1-2) или (1-3), к сумме светимости по всему экрану от излучения идущего от двух некогерентных источников. Как видим, у нас это отношение получилось в 2-а раза больше и оно будет в 4-е раза больше, как пишет Сивухин, если мы его будем сравнивать с энергией излучения от одного некогерентного источника света. А получается так потому, что мы сравниваем излучение на фиктивной интерференционной картинке с излучением одного реального источника света. А интерференционная картинка у нас будет фиктивной потому что светлые полосы на экране горят постоянно. А, если мы рассмотрим реальную интерференционную картинку рассчитанную по формуле (1-4), то мы увидим, что светлые полосы то загораются то гаснут.

Происходит это потому что два фронта напряженности электрического поля, двигаясь навстречу друг другу со скоростью зайчиков напряженности, которая в этом примере получилась равной 11,5 скоростей света, будут в одних точках экрана совпадать с максимальными напряженностями, а в других с минимальными. Но по мере продвижения зайчиков напряженности в этих точках напряженность будет изменятся по синусоидальному закону и поэтому полосы будут понемногу тускнет, а потом погаснут полностью. А при дальнейшем движение зайчиков фазы напряженностей станут такими, что полосы будут понемногу увеличивать свою светимость, т.е. мы будем видеть, моргающие светлые полосы. И в этом случае энергия излучения этих моргающих полос будет точно равна энергии от двух некогерентных источников, т.е. никакого нарушения закона сохранения тут не будет и поэтому не надо и фантазировать о "закромах родины". В общем, оценить творчество математико-физиков можно только строкой из песни В. Высоцкого "остается только материться". А еще приходят на ум вот эти его строки.

Товарищи ученые! Доценты с кандидатами!

Замучились вы с иксами, запутались в нулях

Только я бы в этих строчках, чтобы не обижать всех ученых и, например, инженеров, которые не только создали массу различных сложных наукоемких изделий, но, например, в царской России при испытании сконструированных ими мостов становились лично под этими мостами, заменил бы слово ученые на математико-физики. Уж этим то точно боятся нечего, т.к. их интегралом не придавит, если они произвели какие то расчеты с ошибками. Поэтому они и не задумываются над результатами, которые у них получились. И тут опять на ум приходят разные сравнения, например, с интермедией Аркадия Райкина, которому сшили бракованный костюм, но на все претензии отвечают просто "Пуговицы пришиты крепко? - крепко. Какие претензии?". Так и у математико-физиков "Ошибок в чисто математических преобразованиях нет? - нет. Какие претензии?".

Мне вообще последнее время стало интересно - а математико-физики хоть когда ни будь при своих преобразованиях включают мозги или они автоматически только делят и умножают. А что делить или умножать - землекопов на километры пути или скорость поезда на глубину траншеи им все равно. Так у них происходит и с начальными фазами двух лучей, падающих на экран, при расчете интерференционной картинки. И, когда первый луч, например, в интерферометре Майкельсона прилетает к экрану в момент времени Т1, а второй немного позже в момент времени Т2, то они не задумываясь отвечают, что разность фаз при построении интерференционной картинки будет v0*(T2-T1), где v0 частота источника света, т.е. разность фаз тут получится в периодах колебаний света. Здесь необходимо заметить, что при построении интерференционной картинки нас действительно не интересуют абсолютные значения фаз двух лучей прилетевших к экрану, а интересует только их разность в произвольный момент времени, когда они одновременно коснулись поверхности экрана.

Но по рекомендациям математико-физиков получается, что, когда два фронта двух лучей в интерферометре Майкельсона вылетели с источника одновременно в момент времени Т=0 с фазами N1=N2=0, то фронт первого луча, прилетев к экрану с фазой N1 в момент времени T1, если он прилетел раньше второго луча, так и будет лежать на экране, как кирпич, и ждать, когда к экрану с фазой N2 в момент времени T2 прилетит второй кирпич, чтобы обняться с ним и проинтерферировать. Вот только луч света не кирпич и поэтому фронт волны первого луча после момента времени Т1 полетит дальше, а в момент времени Т2 на экран упадет фронт первого луча, который вылетел из источника в момент времени dT= T2-T1, и теперь в момент времени Т2 его фаза будет N1 + v0*dT = N2, если мы определили N1 и N2 по времени их движения до экрана с постоянной частотой как N1=v0*T1 и N2=v0*T2. Таким образом в момент времени Т2 у нас на экран всегда будут падать два луча с одинаковыми фазами и, следовательно, никакого смещения интерференционных полос при изменении времени движения двух лучей мы не должны наблюдать.

Тоже самое относится и к теории всех подобных экспериментов, например, опыту Физо по определению увлечения света движущимися средами, где наблюдали смещение интерференционных полос при разной скорости среды в которой двигались два луча. Ведь по сути эта установка Физо (так же, как и его установка по определению скорости света) полностью аналогична установке Майкельсона, т.к. там точно так же луч расщепляется на два луча а потом они проходят один и тот же путь, но при движении в среде, которая течет в разных направлениях их скорости распространения, и потом эти лучи попадают в окуляр телескопа, где наблюдают смещение интерференционных полос. А смещение этих полос интерпретируют как результат разности времени движения двух лучей, но т.к. мы выяснили, что разность времени движения двух лучей не имеет никакого отношения к смещению полос, то и все выводы в этом и подобных ему экспериментах, сделанные по величине наблюдаемого смещения полос, никак не доказывают то, что пытались доказать в этих экспериментах. А в опыте Физо это смещение не доказывает частичное увлечение света движущимися средами. Более того, как выяснил Замятин [21], который повторил этот опыт Физо на современном оборудовании, смещение полос в интерферометре возникает ни от скорости потока воды, в которой двигались лучи света, а от изменения давления воды в трубах при ее разной скорости прокачки.

Но такой вывод об отсутствие смещения полос при разном времени движения лучей будет только в том случае, если на всем пути от источника до экрана частота света в лучах будет неизменной и при этом они всегда будут падать в одну и туже точку на поверхности экрана. Ведь, как мы уже выяснили и время движения зайчиков напряженности от точки их падения на экран до конкретной точки на экране тоже отразится на фазе волны в этой точке по формулам (4-1). И, если у нас частота света будет на различных этапах пути лучей от источника до экрана разной, то определять фазы падения двух лучей на экран при времени их движения до экрана T1 и T2 по формулам N1=v0*T1 и N2=v0*T2 нельзя, а надо суммировать количество колебаний света в лучах на всех участках их путей, где они будут двигаться с разной частотой. При этом я могу даже предположить, как считают многие, что в моменты падения лучей на экран, принятая экраном частота света будет равна частоте покоящегося источника света, но ни кто не будет спорить с тем, что, если первый луч отразится от набегающего на него зеркала, то его частота увеличится, а, если второй луч отразится от убегающего от него зеркала, то его частота уменьшиться и, если он отразиться от зеркала движущегося перпендикулярно скорости луча, то его частота не изменится.

Следовательно лучи света, отразившись от зеркал или граней призмы будут лететь с разными частотами и поэтому я при расчете интерференционной картинки обязательно буду использовать в расчете начальных фаз двух лучей их значения N10 и N20, которые получились суммированием колебаний на всех этапах движения лучей с разной частотой обусловленной эффектом Доплера. И такой расчет будет у меня производиться в программе Maikelson1, если на рис. 18 в рамке <расчет начальных фаз двух лучей в точках падения их центров на экран> будет отмечен первый переключатель. Но для сравнения я буду производить и расчеты начальных фаз по времени, т.е. определяя N1 и N2 как N1=v0*T1 и N2=v0*T2, если будет отмечен второй слева переключатель. А, если мы будем начальную фазу первого луча уточнять на время dT, чтобы найти фазы двух лучей для одного и того же момента времени, то для расчета надо будет отметить третий слева переключатель. Здесь есть еще четвертый и пятый переключатели, но на них я остановлюсь ниже.

А сейчас давайте сделаем вывод о том, что в существующей теории интерференции совершенно не решен вопрос определения начальных фаз двух лучей для одного и того же момента времени, которые нужны для расчета интерференционной картинки. И, чтобы уж закончить с теорией интерференции давайте рассмотрим случай, когда углы падения лучей имеют одинаковые знаки, т.е. зайчики напряженности движутся по экрану не навстречу друг другу, а в одном направлении, но с разными скоростями. Ведь в учебниках ничего не говориться о наблюдаемых при этом полосах, где их визуально наблюдаемая ширина будет шириной, как я их назвал, составных полос, а не обычных полос, о которых мы говорили до этого. Но, чтобы убедится в том, что мы при таких углах падения будем получать именно составные полосы, нам надо убедиться сначала, что мы можем пользоваться формулой (5-2) для определения ширины обычных полос. Поэтому я выполнил несколько опытов на своей установке при разных по величине значениях углов падения лучей на экран, когда они имеют разные знаки, т.е. зайчики напряженности движутся по экрану навстречу друг другу, но с разными скоростями.

И в приведенной ниже таблице 3 я даю сначала расстояния от ребра призмы в моей конструкции интерферометра до левого и правого зеркал в миллиметрах, а потом углы падения лучей в градусах A1p и A2p. Значения ras получены для диаметра луча лазера равного нулю, а mod для диаметра луча лазера 2 мм. Затем я привожу ширину полос в микрометрах Bras, рассчитанную по формуле (5-2) с углами падения ras и Bmod, которые получились при моделировании с реальными углами падения лучей mod на интерференционной картинке, где расчет напряженности велся по формуле (1-4), а начальных фаз лучей по формулам (4-1). И в конце я привожу значение Bnab, которое получено по фотографиям с вэбкамеры в натурном эксперименте и отношение Bmod/Bnab. При этом лучи падали на матрицу вэбкамеры (без оптики) с разрешением 640*480 пикселей, где в одном пикселе 2,2 мкм, не напрямую от зеркал, а пройдя через объектив кинопроектора, который я поместил на расстоянии 0,945 м, от ребра призмы и матрицу вэбкамеры я расположил на расстоянии 0,89 м от объектива. Таким образом, при 48-и кратном увеличении объективом изображения на каждый метр расстояния до матрицы получилось увеличение изображения от объектива в 42,7 раза. При этом, если мы при расчете углов падения ras учтем диаметр луча лазера 2 мм, который на призме делится на два луча по 1 мм, то у нас получится расстояние от ребра призмы, куда упали центры лучей, до зеркала на 0,5 мм больше, а от центров падения лучей на грани призмы до экрана на 0,5 мм меньше, чем от ребра призмы. А в этом случае тангенсы углов падения в 1-ом опыте будут 0,0325/0,9445=0,03441, а арктангенс даст углы 1,970 градуса, т.е. так, как и должно быть в реальном эксперименте, где диаметр лазера был примерно 2 мм.

Таблица 3. Расчетная и наблюдаемая ширина полос при разных углах падения лучей на экран

Опыт_____углы_падения_ras__ углы_падения_mod____Bras____Bmod____Bnab____Bmod/Bnab

1 - 32_32___-1,942___+1,942_____-1,970___+1,970_____9,590____9,456____10,60______0,89

2 - 64_32___-3,873___+1,942_____-3,905___+1,970_____6,407____6,343_____7,03______0.90

3 - 96_32___-5,801___+1,942_____-5,831___+1,970_____4,816____4,781_____5,34______0,89

4 - 128_32__-7,717___+1,942_____-7,744___+1,970_____3,865____3,844_____4,12______0,93

Рис. 19. Фотографии полос при разных углах падения лучей на экран, где на левой фотографии расстояние до левого зеркала 32 мм, на следующей 64, затем 96 и на правой 128, а расстояние до правого зеркала оставалось неизменным 32 мм.

Как видим, у меня в расчете ширины полос имеются какие-то систематические погрешности одной направленности, т.к. имеются существенные расхождения между наблюдаемыми и смоделированными данными, хотя есть и незначительные случайные погрешности. К систематическим погрешностям можно отнести то, что я с какой то погрешностью определил размер пикселей на своих вэбкамерах и коэффициент увеличения изображения объективом кинопроектора, а также то, что длина волны моего лазера могла отличаться от значения (650 нм), приведенного в описании китайскими товарищами, изготовляющими эти лазерные модули. Конечно же отразится на результате в натурном эксперименте и то, что луч лазера у меня расходился, хотя и оставался довольно таки узким, а это при моей схеме интерферометра приводит к тому, что после деления общего луча на ребре призмы на два луча, скорость средних точек этих отдельных лучей уже будет направлена не строго вертикально при их падение на призму, как подразумевалось при моделирование, а под некоторым углом. Да, программа Maikelson1 позволяет учесть эту конусность в расчетах, но я не стал этого делать, чтобы не внести еще большую погрешность в расчетные данные от неправильного определения параметров конуса луча.

Поэтому, конечно же, при проведении точных количественных измерений надо будет уточнить все эти параметры установки. Но, пока нам до этого еще далеко, т.к. у меня осталось еще много чисто теоретических вопросов даже по теории интерференции, например, по определению расчетного значения ширины составных полос. А к случайным погрешностям следует отнести ошибки в измерении расстояний от ребра призмы до точек на зеркалах, куда они падают, и то, что, регулируя углы наклона зеркал, я не мог этого сделать так, чтобы лучи падали точно в середину объектива кинопроектора, т.к. при использовании красного лазера их пятна плохо видны на объективе (да и на зеркалах тоже). И, если вы посмотрите на время проведения этих 4-х опытов на фотографиях полос с вэбкамеры на рис. 19, то увидите, что на перенастройку зеркал у меня ушло всего-навсего чуть больше получаса, т.к. я боялся, что при большой разнице во времени между опытами на их результаты могут повлиять какие то внешние факторы, которые я не смогу учесть. Этим объясняется и то, что полосы в этих опытах получились не очень четкие, хотя, вынужден заметить, что при таких маленьких размерах полос получить их четкие изображения довольно проблематично.

Рис. 20. Изображение интерференционных полос (зеленые полосы) полученных по формуле (1-4) на экране, ширина которого рассчитана для 10-ти полос с шириной полос рассчитанной по формуле (5-2) с углами падения полученными при моделирование, где номера полос нанесены на рисунки. Под рисунками приведены синусоиды изменения напряженности зайчиков для одного из моментов времени. На верхних рисунках картинки для 1-го и 2-го опытов, а на нижних для 3-го и 4-го. Скриншоты программы Maikelson1.

Но я и не стремился при проведении этих опытов к высокой точности, т.к. в случае неправильного расчета ширины полос по формуле (5-2) наблюдаемые и расчетные данные должны были значительно отличаться, а у нас имеется только систематическая погрешность. А теперь давайте немного остановимся на картинках на рис. 20. Что касается 1-го опыта, то здесь все ясно, т.к. при моделировании все полосы загораются одновременно и в одних и тех же местах, а вот в остальных опытах мы видим, что полосы хотя и загораются в одних и тех же местах, но не все одновременно. Например, во 2-м опыте полосы при моделировании загораются и гаснут с номерами через две полосы. А на рисунке изображен момент времени, когда у нас загорелись полосы с номерами -5, -2, +1,+4, а затем они погаснут и загорятся полосы -4, -1, +2,+5 и т.д. В 3-м опыте полосы загораются с периодичностью через одну полосу. На рисунке у нас загорелись полосы -4, -2, 0, +2, +4, а затем они погаснут и загорятся полосы -5, -3, -1, +1, +3, +5. А вот в 4-м опыте я даже не стал искать никакой закономерности, т.к. тут номера светящихся полос изменяются по очень сложной зависимости. Например, на рисунке мы видим яркими полосы -4, -2, +1, +3, а потом могут загореться полосы -4, -1, +1, +4 или -5, 0, +5 или -3, -1, +2, +4 и т.д.

Естественно, при проведении натурных экспериментов мы всего этого не видим, т.к. полосы загораются и гаснут с очень большой частотой и зафиксировать этот процесс мы не можем даже самыми скоростными видеокамерами. А глаз человека вообще может это заметить если периодичность загорания полос будет больше примерно 0,1 с. Таким образом, полученные мною наблюдательные данные не только подтверждают возможность расчета ширины полос по формуле (5-2) и при разных углах падения лучей на экран (если углы имеют разные знаки), т.е. когда полосы загораются и гаснут не только одновременно в одних и тех же местах экрана, но эти данные подтверждают и правильность расчета интерференционной картинки по формуле (1-4). Впрочем, с таким же успехом мы можем использовать и формулу (1-3), но в первоначальном варианте, когда я использовал в ней текущие напряженности, т.к. ширина полос по этой формуле получается точно такая же, как и по формуле (1-4). Единственным отличием здесь будет только ширина самой светлой полоски, что объясняется некоторым искажением строго синусоидальной зависимости суммарной напряженности в различных точках экрана при расчете по формуле (1-3). Например, на рис. 21 показано смещение полос на 0,2 ширины полос при моделировании с использованием этих двух формул, когда у нас задана разность фаз Q2-Q1=0,2. Но это искажение ширины светлой полоски может быть даже достоинством формулы (1-3), т.к. светлая полоска получается более узкой и поэтому у нас более наглядно будет видно смещение полос, хотя программа сама определяет это смещение одинаково точно при расчете по обоим формулам.

Рис. 21. Смещение полос при разности фаз Q2-Q1=0,2. Слева при расчете по формуле (1-4), а справа по формуле (1-3). Скриншот программы Maikelson1.

А вот что касается аналитического расчета ширины составных полос и их смещения, то здесь у меня пока еще есть некоторые вопросы. Ведь вывод формул (5-1) и (5-2) базируется на разности хода двух лучей до произвольной точки на экране, и эта разность принимается равной одной длине волны, т.е. эти формулы выводились для расчета ширины обычных полос, из которых будут состоять составные полосы, а ширина составных полос должна зависеть от разности скоростей зайчиков напряженности. Например, что касается скриншота на левом рис. 22, где у нас углы падения лучей одинаковые, но имеют разные знаки, то здесь ширину обычной полосы можно определить по формуле (5-3) и она будет точно равна значению рассчитанному по формуле (5-2). Я для удобства восприятия прочитанного здесь повторю формулу (5-2) и приведу некоторые параметры двух лучей (у меня здесь принята скорость света в воздухе Vs=299910 км/с, а длина волны моего красного лазера 0,65 мкм, что при данной скорости света будет соответствовать его частоте v01=v02= 4,614*10^14 Гц).

Рис. 22 Варианты интерференционных полос, которые могут наблюдаться. Слева обычные полосы при разных знаках углов падения лучей на экран A1p= +5 и A2p= -5 градусов. Справа составные полосы, которые образуются из нескольких обычных полос при одинаковых знаках углов падения лучей на экран A1p= +5 и A2p= +6 градусов. Внизу показаны синусоиды (красная и синяя) изменения напряженности поля двух лучей, которые как бы движутся или навстречу друг другу (слева) или в одну сторону (справа). Скриншоты программы Maikelson1.

При этом у меня ширина полосы, рассчитанная по формуле (5-2) получилась 3,73 мкм, что соответствует интерференционной картинке рассчитанной с использованием скоростей движения зайчиков по экрану, ширина которого на левом рисунке для четырех полос составит 14,92 мкм. А длина волны зайчиков напряженности двух лучей получается по 7,46 мкм, но здесь, т.к. скорости зайчиков Ve1= -11,47*Vs и Ve2= +11,47*Vs имеют разные знаки, то и L1= Ve1 / v01= -7,46 мкм и L2= Ve2 / v02= +7,46 мкм тоже будут иметь разные знаки, что нам потребуется в дальнейшем. А сейчас мы можем констатировать, что в этом частном случае у нас ширина полос будет равна половине длины волны зайчиков напряженности. Ведь полосы у нас будут светится в те моменты, когда две синусоиды зайчиков напряженности совпадут и в тех местах, где будут максимумы напряженностей (с положительными или отрицательными значениями) появятся две светлые полосы, т.е. на одной длине волны зайчиков напряженности будет две полосы. А сейчас давайте попробуем получить формулу расчета ширины полос для общего случая, когда углы падения будут не равны и, следовательно, у нас будут две синусоиды с разной длиной волны, которые никогда не совпадут.

B= L0 / (sin(A2p) - sin(A1p)) (5-2)

B= (L2 - L1) / 4 (5-3)

B= (L2 * L1) / (L2 - L1) (5-4)

B= (L2 * L1) / (L2 + L1) (5-5)

И поможет нам в этом правый рис. 22, где у нас углы падения имеют одинаковые знаки и незначительно отличаются друг от друга. Здесь получается, что максимумы и минимумы напряженностей двух зайчиков будут примерно совпадать в те моменты времени, когда у нас разность фаз зайчиков напряженности будет равна одному периоду. Поэтому, как ни странно, но для вычисления ширины получающихся при этом составных полос отлично подходит формула (5-2), которая и выводилась для разности хода двух лучей в одну длину волны, т.е. в нашем случае это будет изменение разности фаз на один период. Здесь получается по формуле (5-2) ширина полосы 37,42 мкм и смоделированная мною интерференционная картинка при ширине экрана 74,83 мкм тоже дает ширину составной полосы 37,42 мкм. А объяснить это с точки зрения движения по экрану синусоид зайчиков напряженности можно так. У нас фазы двух зайчиков совпадут в тот момент, когда из за разности скоростей движения двух синусоид их максимумы сместятся друг относительно друга на одну длину волны. Например, при наших значениях скоростей зайчиков Ve1= -11,47*Vs и Ve2= -9,57*Vs и значениях их длин волн L1= Ve1 / v01= -7,46 мкм и L2= Ve2 / v02= -6,22 мкм, у нас до этого момента должно произойти L2 / (L2 - L1)= -5,016 периодов колебаний зайчиков первого луча. Умножаем это на длину волны зайчика первого луча -7,46 мкм и получаем 37,42 мкм. Таким образом, здесь ширину составных полос можно рассчитать и через длину волны зайчиков напряженности по формуле (5-4).

А вот теперь мы можем по аналогии получить не частную формулу (5-3), а общую формулу для определения ширины полос получающуюся при углах падения лучей имеющих разные знаки. И у нас получится формула (5-5), которая тоже дает точно такой же ответ, как и формула (5-2) при встречном движении зайчиков напряженности. Многие могут задаться вопросом - а зачем нам эти зайчики напряженности и полученные с их помощью формулы (5-4) и (5-5), если те же значения ширины полос мы можем получить и по формуле (5-2). На это я могу ответить так. Если вы не хотите вникать в физику рассматриваемых вами явлений, а хотите только делить и умножать, то вам это действительно не нужно. А, если вы хотите вникнуть в суть рассматриваемых явлений, то без зайчиков напряженности это сделать крайне сложно. Например, они нам уже помогли наглядно определить на рис. 15 как будет изменяться фаза в лучах света в разных точках экрана и что ширина полос, рассчитанных для случая на правой картинке рис. 22, не имеет никакого отношения к ширине обычных полос, которые мы наблюдали на левой картинке, а является шириной составных полос. А вот ширину отдельных полос в этом случае нам поможет определить только формула (5-5), которая дает значение 3,39 мкм. Проверяем это непосредственно замеряя расстояние между шестью светлыми полосками в составной полосе и получаем 20,31/6= 3,385 мкм. А далее нам зайчики напряженности позволят разобраться и с другими сложными случаями явления интерференции.

Например, давайте рассмотрим левую картинку на рис. 23, где у нас углы падения значительно отличаются друг от друга, например, в 10 раз или в 20 раз, что гораздо больше, чем в примерах рассмотренных нами на рис. 19 и 20. Здесь у нас углы падения будут -1 и -20 градусов, но почти такая же картинка будет и, если углы будут иметь разные знаки, т.е. +1 и -20. Согласно формулам (5-2) и (5-4) у нас будет расчетная ширина полос 2,00 мкм, но мы видим на рисунке не только эти узкие полоски, а так же и составные полосы ширину которых мы можем определить кликнув мышкой в середины двух соседних составных полос и у нас получится примерно 19 мкм. Таким образом, оказывается, что в этом случае (в отличие от примера на правой картинке рис.22) нам те же формулы (5-2) и (5-4) дают не размер ширины составной полосы, а ширину отдельной обычной полосы. И выяснить это нам помогают значения длин волн зайчиков напряженности, которые получились у нас L1=+37,2 и L2=+1,9 мкм при Ve1=+57,3*Vs и Ve2=+2,9*Vs. Ведь из нижней части картинки видно, что составные полосы образуются в тех местах, где первая синусоида (красная) имеет максимумы и минимумы, т.е. ее ширина определяется длиной волны первого зайчика напряженности. А синусоида второго луча (синяя) делит эти участки первой синусоиды на отдельные полоски, высвечивая только те места, где совпадают ее максимумы или минимумы с максимумами или минимумами первой синусоиды. И отсюда ясно, что ширина составных полос будет примерно равна половине длины волны 1-го зайчика, т.е. 37,2 / 2= 18,6 мкм.

Рис. 23. Варианты интерференционных полос, которые могут наблюдаться у составных полос. Слева при большой разнице углов падения лучей на экран A1p= -1 и A2p= -20 градусов. Справа при разных знаках углов падения лучей на экран и небольшом отличие их по модулю A1p= +5 и A2p= -4 градуса. Внизу показаны синусоиды изменения напряженности поля двух лучей, которые как бы движутся или в одну сторону (слева) или навстречу друг другу (справа). Скриншоты программы Maikelson1.

При этом составные полосы постоянно движутся вместе с 1-ой (красной) синусоидой вправо, но в реальных экспериментах мы этого увидеть не сможем, т.к. скорость смещения синусоиды будет очень большой Ve1=+57,3*Vs, а такую скорость не могут зафиксировать никакие приборы. Таким образом визуально мы при этом должны будем наблюдать на ширине всего экрана только отдельные узкие полоски, которые с очень большой частотой будут загораться и гаснуть в одних и тех же местах на экране в те моменты, когда составные полосы будут с большой скоростью подходить к этим участкам экрана. И примерно такую же картинку мы будем видеть и в том случае, если у нас углы падения будут иметь разные знаки но близкие значения по модулю, например, A1p= +5 и A2p= -4 градуса, как это отражено на правой картинке рис. 23. Здесь у нас получается L1= -7,45 и L2=+9,32 мкм при Ve1= -11,5*Vs и Ve2=+14,3*Vs, а ширина составной полосы измеренная по картинке получится примерно 37,5 мкм (на рисунке мы видим две синее линии между номерами полос -9,-8 и +9,+10 в местах, где я кликнул мышкой в программе и получил после этого ширину двух полос 75 мкм). А вот формулы (5-2) и (5-4) дают нам ширину отдельных полос 4,14 мкм и таким образом мы видим, что и в этом случае в отличие от примера на правой картинке рис. 22 эти формулы дают здесь не ширину составной полосы.

И здесь опять нам на помощь приходит формула (5-5), которая дает значение ширины полосы 37,4 мкм, что очень близко к наблюдаемому нами значению на картинке 37,5 мкм. Но, как и с вариантом составных полос на левой картинке, это опять таки не пригодится нам при проведении натурных экспериментов, т.к. и в этом случае скорость перемещения составных полос по плоскости экрана будет очень большой. А конкретно в этом случае по полученному графику смещения центра составной полосы у меня получается ее скоростью 112*Vs, хотя сумма встречных скоростей зайчиков будет 25,8*Vs, но и это очень много. И таким образом можно сделать вывод о том, что в натурных экспериментах мы сможем наблюдать визуально или фиксировать приборами составные полосы только в том случае, когда углы падения лучей на экран будут иметь один знак и незначительно отличаться по модулю. А во всех остальных случаях мы будем наблюдать обычные полосы. Но, чтобы знать какие полосы мы наблюдаем, надо знать какие у нас в эксперименте были углы падения лучей на экран, а, как я уже писал выше, все, кто проводил эксперименты с интерферометром Майкельсона не могут ответить на этот вопрос. Поэтому нам надо сейчас выяснить на сколько будут смещаться составные полосы при заданной разности фаз двух лучей, т.к. возможно, что в натурных экспериментах наблюдали и смещение составных полос.

Для этого опять обратимся к расчету интерференционной картинки для примера на правой картинке рис. 22, где у нас были углы падения двух лучей A1p= +5 и A2p= +6 градусов. Давайте выполним три расчета интерференционной картинки для трех комбинаций начальных фаз двух лучей 0 и 0; 0,3 и 0; 0,6 и 0, где фазы заданы в долях периодов колебаний света в двух лучах. На верхних картинках рис. 24 отражен 1-ый вариант, на средних 2-ой и на нижних 3-ий. Как видим, и составные полосы при разности начальных фаз двух лучей смещаются на ту же величину, что и отдельные полосы, как это отражено на рис. 21. При этом, если мы зададим угол падения 2-го луча не +6, как на левых картинках, а +4, как это отражено на правых картинках, то у нас смещение составных полос будет происходить при той же разности фаз в другую сторону. Таким образом у нас получается, что, даже, если при проведении натурных экспериментов на установке Майкельсона углы наклона зеркал были такие, что давали составные полосы, то это все равно не должно было отразиться на результатах этих экспериментов, где не фиксировалось направление смещения полос, а определялась только величина этого смещения.

Рис. 24. Смещение составных полос при разности фаз в двух лучах 0, 0,3 и 0,6 периода. Слева при A1p= +5 и A2p= +6 градусов, а справа при A1p= +5 и A2p= +4 градуса. Скриншоты программы Maikelson1.

5. Теоретическая проверка результатов выполненных на установке Майкельсона.

Все экспериментаторы, которые проводили натурные эксперименты на установке Майкельсона, получили примерно одинаковые результаты, которые с использованием теории этого эксперимента, созданной Майкельсоном и подправленной Лоренцем, давали значение абсолютной скорости Земли заниженное примерно в четыре раза по сравнению со значением скорости Земли относительно Солнца. Т.е. даже с точки зрения теории этого эксперимента, созданной Майкельсоном, они получали явно абсурдный результат, но ни кто до сих пор так и не удосужился выяснить почему же так происходит, т.е. ни кто не постарался исправить теорию этого эксперимента, чтобы она давала те значения смещения полос, которые наблюдались при проведение экспериментов. Все они стремились только увеличить длину плеч интерферометра, т.к. с их увеличением прямопропорционально должна была увеличиваться и величина разности времени движения двух лучей до экрана, а согласно использованной ими теории и разность фаз двух лучей, которая должна приводить к увеличению смещения полос. Ведь в первом эксперименте, выполненном Майкельсоном в 1881 году, где у него плечи интерферометра были по 1,2 метра, расчетное смещение полос должно было быть всего-навсего +/- 0,02 ширины полосы, что в сумме давало 0,04 ширины полосы. Я тоже крутанул установку собранную по схеме Майкельсона с плечами по 0,4 м в горизонтальной плоскости, чтобы посмотреть будут ли при этом наблюдаться смещения полос [26]. К сожалению, я при повороте установки на 360 градусов не смог зафиксировать достоверных значений смещения полос (не говоря уже о фиксации смещения полос на сотые доли их ширины), т.к. малейшие колебания почвы, например, от проезжающих на улице машин или мотоциклов, а также микровибрации в подвеске установки из-за наличия сухого трения в материале подвески, приводили к заметному дрожанию полос.

Более того, в этом видеофайле [26] мы видим, что у нас наблюдается и заметное смещение полос в правую сторону при вращение установки против часовой стрелки и смещение полос в левую сторону при вращение установки по часовой стрелке, т.е. наблюдается полнопериодический эффект. А из того, что при вращение установки в разные стороны у нас происходит и смещение полос в разные стороны, напрашивается вывод о влияние на такое смещение полос эффекта Доплера. Да, на зеркале, плоскость которого расположена перпендикулярно радиусу вращения установки, никакого эффекта Доплера не должно быть, но на зеркале, плоскость которого расположена почти параллельно радиусу вращения обязательно должен быть эффект Доплера. И, когда установка вращается против часовой стрелки это зеркало удаляется от падающего на него луча света, а когда она вращается по часовой стрелке наоборот приближается. Следовательно, в одном случае частота второго луча, падающего на экран, будет меньше частоты первого луча, а в другом случае наоборот больше. А это и должно приводить к смещению полос то в одну, то в другую сторону. Поэтому я решил повторить этот эксперимент увеличив скорость вращения установки и для этого перед началом эксперимента закрутил нить, на которой подвешена установка, так, чтобы при раскручивание нити установка делала не один оборот, а несколько оборотов.

Как я и ожидал, результатом этого эксперимента (см. видеофайл [27]) явилось то, что полосы сместились на гораздо большую величину, а это прямо доказывало то, что это смещение вызвано именно эффектом Доплера. Но, тут не все так просто. Если вы внимательно присмотритесь к смещению полос относительно какой то точки на экране, которые все являются пылинками попавшими на матрицу вэбкамеры, то вы заметите, что смещение полос происходит очень не равномерно. Причем скорость их смещения не коррелируется напрямую со скоростью вращения установки, а зависит еще от каких то факторов. Поэтому объяснять в этих экспериментах смещение полос только эффектом Доплера не получится. Возможно, что здесь оказывает свое влияние и аберрация луча лазера от скорости вращения установки, но проверить это сейчас я не могу, т.к. при создание математических моделей установок Майкельсона и своей, я не предусмотрел вращательного движения установок. Возможно, что я этим займусь при следующем этапе своих исследований, а сейчас по тому, что я наблюдаю в этих двух экспериментах, я должен сделать вывод о том, что на собранном мною интерферометре Майкельсона я не могу измерить смещения полос вызванные линейной скорости движения установки при разных углах поворота установки в пространстве.

Поэтому я снимаю шляпу перед гением инженерной мысли и трудолюбием и выдержкой экспериментаторов, которые смогли на установке Майкельсона зафиксировать смещение полос, которое дало хоть какие то результаты по скорости Земли при ее движении в неподвижном эфире. Вот только получали все они этот результат абсолютной скорости Земли используя разность фаз двух лучей прилетающих не одновременно к экрану. Но, как мы выяснили, эта разность времени движения двух лучей до экрана никак не должна была привести к смещению полос. Поэтому интересно выяснить что же конкретно могло приводить к наблюдаемому ими смещению полос. И здесь напрашивается вывод о том, что к этому могло привести смещение фаз, вызванное тем, что при повороте установки лучи падали не все время в одну и ту же точку на экране, а, следовательно, согласно формулам (4-1), у нас должна была изменяться и начальная фаза лучей. Но прежде, чем проводить вычислительные эксперименты для проверки этого предположения, надо выяснить какие углы наклона зеркал могли быть при проведении этих экспериментов и какие при этом получались углы падения лучей на экран. А вот тут у нас возникает главная проблема, т.к., например, Майкельсон и Морли [2] по этому поводу вообще ничего не написали, если не считать вот этих двух цитат

"... зеркала регулировались с помощью винтов в кронштейнах, которые держали зеркала и к которым зеркала прижимались пружинами, регулировка проводилась до тех пор, пока свет от обоих лучей не становился виден в телескоп ...".

"Разница длин двух оптических путей затем ликвидировалась перемещением зеркала e1.Это зеркало имело три вида регулировки; оно регулировалось по высоте и по азимуту так же, как и другие зеркала, но более точно, оно также имело регулировку вдоль направления падающего луча, смещаясь вперед или назад, но оставаясь точно параллельно своей бывшей плоскости."

А Миллер [3] немного пишет о регулировках зеркал, хотя ничего не пишет о регулировке полупрозрачной пластины, но зачем то очень много пишет о том какие лампы он использовал при настройке интерферометров для проведении экспериментов в разные годы. А потом пишет, что " Монохроматические полосы в наблюдениях эфирного ветра никогда не применялись" и даже более того их не надо использовать и при настройки интерферометра, кроме случаев перемонтажа всей установки. Но у Миллера все же есть очень забавные данные об углах наклона зеркал, которых нет в отчетах других экспериментаторов, а конкретно он пишет, что "Ширина полос и число полос в поле зрения прямо зависят от отклонения концевого зеркала. Угол отклонения света на зеркале, как это было в данных эксперимента, составил от 0° до ±4''.", т.е. получается +/- 0,0011 градуса. А простейший расчет по формуле (5-2) показывает, что при таких углах падения лучей на экран (0 и 0,0011 градуса) мы должны были наблюдать полосы шириной около 9 мм, а в таком случае нам не нужна не только труба телескопа, но даже очки. И при этом он написал "К несчастью, ни в каких наблюдениях, сделанных до сих пор, не проводилось числовое измерение ширины полос". Вот только я не пойму, а что же он сам то не проверил какая будет ширина полос при указанных им углах наклона одного из зеркал.

В общем, мы видим, что все экспериментаторы крутили туда и сюда все, что шевелится, до тех пор пока не появлялись четкие полосы, а какие при этом были углы наклона зеркал и полупрозрачной пластины они понятия не имели. Поэтому рискну предположить, что углы наклона зеркал у них были значительно больше. Здесь, правда, есть еще вариант как уменьшить ширину полос при таких маленьких углах наклона зеркал. Для этого надо сделать угол наклона полупрозрачного зеркала не 135 градусов. Например, на левом рис. 25 мы видим, что при угле наклона полупрозрачной пластины 134 градуса, у нас углы падения лучей в статике получаются A1= +2 градуса и A2= -2 градуса. А, если мы обратим внимание на статью Майкельсона 1881 года, то поймем, что основная регулировка производилась именно изменением угла наклона в вертикальной плоскости и угла поворота в горизонтальной плоскости полупрозрачной пластины b. Вот цитата из его статьи [1].

"Зеркала с и d насколько возможно продвигались к пластине b и с помощью винта m выравнивались в пределах двух диапазонов расстояния между точкой на поверхности в и двумя зеркалами. Зажигалась лампа, делалось небольшое отверстие в экране, размещенном перед ней, которое и служило источником света; пластина b, которую можно регулировать в двух плоскостях, двигалась вокруг, пока два изображения точки света, которые отражались зеркалами, не совпадали. Затем фонарь с пламенем натрия размещался в a, и создавались интерференционные полосы. Полосы могли меняться по ширине, положению и направлению небольшим перемещением пластины b, и когда достигалась удобная ширина и максимальная четкость, натриевое пламя устранялось, и его опять заменяла лампа. Винт m затем медленно поворачивался до тех пор, пока вновь не появлялись полосы. Они были, разумеется, цветными, кроме центральной полосы, которая была почти черной."

Таким образом, здесь мы видим, что основная регулировка у него производилась поворотом вокруг вертикальной оси полупрозрачной пластины 3 на левом рис. 25. И доказательством именно этого вывода является то, что все экспериментаторы использовали белый свет, а он дает одну полосу нулевого порядка (как в опыте Юнга со светом на двух щелях), которая отличается от всех остальных полос, если углы падения лучей имеют разные знаки. А проще всего этого добиться немного отклонив полупрозрачную пластину 3 от исходного значения 135 градусов. А все экспериментаторы почему то считали необходимым условием проведения таких экспериментов именно наличие этой полосы нулевого порядка. И, если мы зададим угол наклона полупрозрачной пластины отличный от 135 градусов, то в этом случае у нас углы падения лучей на экран, покоящийся в АСО, всегда будут разных знаков при исходных значениях углов наклона зеркал Alfa1=90 и Alfa2=0 градусов. Но при движение установки в разных направлениях углы падения лучей на экран, покоящийся в АСО, будут постоянно изменяться, т.к. при этом будет и аберрация луча лазера и отклонение эффективных углов наклона зеркал от их статических значений.

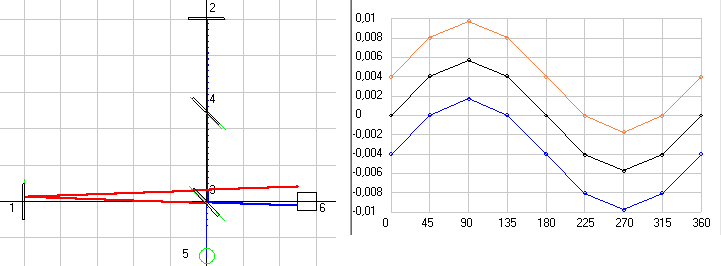
Рис. 25. Слева скриншот программы Maikelson1, где отражены траектории движения света в лучах (первый красный и второй синий) в установке покоящейся в АСО при угле наклона полупрозрачной пластины 3 не 135 градусов, как подразумевается по умолчанию у всех авторов, а 134 градуса. Справа углы падения лучей на экран в АСО при разных углах направления движения Земли с абсолютной скоростью Vz= 30 км/с. Верхняя синусоида это изменение угла падения 1-го луча при угле наклона 1-го зеркала Alfa1=90,002 градуса, а нижняя 2-го луча при угле наклона зеркала Alfa2=0,002 градуса и средняя синусоида для обоих лучей, когда Alfa1=90 или Alfa2=0 градусов. Графики построены с использованием программы Grafik4.

А в этом случае, как мы видим на правом рис. 25, у нас, если одно из зеркал будет отклонятся от 0 или 90 градусов на 0,002 градуса, то возможны случаи, когда при одном угле поворота установки углы падения лучей на экран будут иметь разные знаки (например, при 20 градусах) и мы должны в этом случае наблюдать полосу нулевого порядка, а при другом угле поворота установки (например, при 90 градусах) оба угла падения лучей на экран будут иметь одинаковые знаки и мы в этом случае не должны наблюдать полосу нулевого порядка. Более того, в последнем случае мы должны будем наблюдать составные полосы, которые визуально будут восприниматься как полосы равного угла наклона. Но на самом деле у нас наблюдаемые углы падения лучей на экран при повороте установки изменяться не будут, т.к. после перевода составляющих (по осям координат) скоростей света движущегося в АСО в ИСО экрана у нас будут получаться все время одинаковые углы падения лучей на экран, как это отражено далее в таблицах 4, 5, 6 и 7 для этих углов A1iso и A2iso.

А при проведении натурных экспериментов на установке Майкельсона я при регулировке угла поворота пластины 3 иногда получал и очень странные полосы, которые почему то были не чувствительны к различным вибрациям. И даже, когда я рукой наклонял верхнюю часть зеркал в одну и другую сторону, т.к. корпус крепления зеркал был не абсолютно жестким, эти полосы не пропадали, а только изменяли свой угол наклона на противоположный, как это показано в этом видеофайле [28]. Чем это вызвано я так и не понял, т.к., когда я регулировал пластину 3 с падением лучей не на объектив кинопроектора и потом на экран, а сразу на матрицу вэбкамеры, я таких полос не видел. При этом у меня в установке Майкельсона была пластина полупрозрачная с обоих сторон, которую я вынул из старого CD-ROM, а поэтому при использовании пластины полупрозрачной с одной стороны этих полос может и не быть даже при использовании оптики для увеличения изображения. Хотя, какая бы стеклянная пластина у нас не была, все равно отражение света будет происходить от обоих сторон пластины. Только яркость луча, отраженного от прозрачной поверхности, будет гораздо меньше, чем от посеребренной полупрозрачной.

А теперь давайте вернемся к моей гипотезе о том, что наблюдаемое в этих экспериментах смещение полос могло быть вызвано изменением координат точек падения лучей на экран, что согласно формулам (4-1) должно приводить к изменению фаз в лучах света. На левом рис. 26 представлены графики координат падения лучей в АСО по оси Y при разных направлениях движения Земли, которые показывают, что при абсолютной скорости Земли Vz= 30 км/с у нас координаты их падения периодически изменяются так же, как и изменялись углы падения этих лучей на правом рис. 25. И отклонение угла наклона зеркал от исходного положения Alfa1=90 и Alfa2=0 градусов на 0,002 градуса приводит к синхронному изменению и координат падения лучей. При этом толщина стеклянных пластин практически не влияет на эти отклонения по координатам от исходного положения, но на их исходное положение координат она влияет.

Все эти данные были получены мною при проведении серии вычислительных экспериментов на математической модели установки Майкельсона с длинами плеч по 11 метров, которые и были в эксперименте Майкельсона-Морли в 1887 году. При этом оптическая плотность стеклянных пластин была задана равной 1,5, а их толщина задавалась или 2 мм или 12,5 мм. Конкретно у Майкельсона и Морли толщина стекол была 12,5 мм. А вот экран 6 и прозрачная (компенсационная) стеклянная пластина 4 были размещены мною на расстоянии 1 метр от полупрозрачной пластины 3, т.к. о этих значениях в их статье ничего не говорится. При этом, как мы уже выяснили, ни кто из экспериментаторов не указал в своих статьях какие у них были углы наклона зеркал и полупрозрачной пластины. Поэтому я задал произвольные углы наклона зеркал Alfa1=+90,01 и Alfa2= -0,02, а углы наклона стеклянных пластин Alfa3=135 и Alfa4=135 градусов. И хотя при этом мы будем наблюдать не обычные полосы с наличием полосы нулевого порядка, а составные, где не будет полосы нулевого порядка, нам это ни сколько не помешает определить смещение полос от их исходного положения. А как такие углы наклона зеркал повлияют на результат, я покажу далее в таблицах 4, 5, 6 и 7.

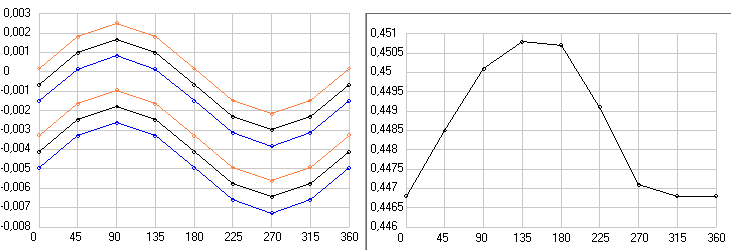
Рис. 26. Слева графики изменения координат падения двух лучей на экран (в метрах) в АСО при разном направление движения Земли с абсолютной скоростью Vz= 30 км/с. Верхние три графика при толщине стеклянных пластин 2 мм, а нижние при их толщине 12,5 мм. При этом средние синусоиды соответствуют углам наклона зеркал Alfa1=90 и Alfa2=0, а верхние углам наклона Alfa1=90,002 и нижние углам наклона Alfa2=0,002. Справа график смещения полос со стеклянными пластинами толщиной 12,5 мм при разном направлении движения Земли с абсолютной скоростью Vz= 30 км/с и Alfa1=90,01 и Alfa2= -0,02. Графики построены с использованием программы Grafik4.

Теперь давайте посмотрим, что ожидали увидеть авторы, проводившие натурные эксперименты, когда они рассматривали движение установки в двух направлениях вместе с Землей при абсолютной скорости установки Vz= +/- 30 км/с и, что получится у нас при моделировании их эксперимента. Согласно данным Майкельсона и Морли они в соответствие с теорией этого эксперимента, созданной Майкельсоном и подправленной Лоренцем, ожидали увидеть смещение полос на +/- 0,02 их ширины, т.е. в сумме должно получиться 0,04 ширины полосы. А математическая модель дает нам график изображенный на правом рис. 26, где при расчете интерференционной картинки использовалась формула (1-4), а начальные фазы двух лучей определялись по 3-ей методике, описанной мною выше и на которой я еще подробно остановлюсь далее, и конечные фазы света двух лучей в разных точках экрана определялись по формулам (4-1). При этом координаты падения лучей полученные в АСО перед их применением в формулах (4-1) как и углы падения лучей и скорости движения зайчиков напряженности приводились к ИСО экрана.

Как видим, у нас тут смещения полос получаются просто микроскопические, т.е. измеряются тысячными долями от ширины полосы, поэтому для более точного их определения программой Maikelson1 мне пришлось сделать ширину экрана равной только двум ширинам полос и увеличить изображение в пять раз, что дало ширину экрана 2500 пикселей (при стандартной ширине 500 пикселей), а также пришлось вычислять среднее значение смещения полос на некотором интервале времени. Обратите внимание на то, что если вы будете самостоятельно повторять данные полученные в этих вычислительных экспериментах, то те же данные по смещению полос вы получите только при том же заданном количестве полос на экране и при том же масштабе, а в противном случае эти данные будут немного отличаться от приведенных мною.

Т.е. при абсолютной скорости движения установки вместе с Землей Vz= +/- 30 км/с у нас получается суммарное смещение полос 0,4508 - 0,4468= 0,004 их ширины. Но ведь у нас Земля движется сквозь эфир не только с ее скоростью относительно Солнца, но еще и с абсолютной скоростью Солнца, которая по разным данным составляет сотни километров в секунду. Давайте примем, что это у нас установка вместе с Землей движется со скоростью Солнечной системы Vss= 300 км/с в разных направлениях (от 0 до 315 градусов) и посмотрим какие у нас будут смещения полос. При этом сделаем четыре серии вычислительных экспериментов. Две серии для наблюдения обычных полос и две серии для наблюдения составных полос. И зададим при этом разные углы наклона зеркал, чтобы получить разные значения ширины как обычных, так и составных полос. Полученные при этом результаты я привожу в таблицах 4, 5, 6 и 7, где A1aso и A2aso это углы падения лучей в АСО, а A1iso и A2iso эти же углы после приведения их к ИСО экрана и B и dB это ширина полос, рассчитанная по формуле (5-2), и смещение полос в долях B. А на графиках рис. 27 я отразил результаты по смещению полос согласно данным этих таблиц.

Таблица 4. Углы падения лучей в АСО и ИСО экрана при разных углах направления движения установки со скоростью Vss=300 км/с для Alfa1=+90,01 и Alfa2= -0,02 и получающиеся при этом ширина полос B и их смещение dB в долях B.

___________0________45_______90_______135_______180______225_______270_______315

A1aso____+0,020____+0,060____+0,077____+0,061____+0,020____-0,020_____-0,037____-0,020

A2aso____+0,040____+0,080____+0,097____+0,081____+0,040____-0,000_____-0,017____-0,000

A1iso____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020

A2iso____+0,040____+0,040____+0,040____+0,040____+0,040____+0,040____+0,040____+0,040

B________1856,7____1862,1____1867,4____1862,1____1856,8____1862,1____1867,5____1862,1

dB_______0,4225____0,4586____0,4709____0,4566____0,4552____0,4665____0,4468____0,4149

Таблица 5. Углы падения лучей в АСО и ИСО экрана при разных углах направления движения установки со скоростью Vss=300 км/с для Alfa1=+90,02 и Alfa2= +0,02 и получающиеся при этом ширина полос B и их смещение dB в долях B.

___________0________45_______90_______135_______180______225_______270_______315

A1aso____+0,040____+0,081____+0,097____+0,081____+0,040____-0,001_____-0,017____-0,001

A2aso____-0,040____+0,001____+0,017____+0,001____-0,040____-0,081_____-0,097____-0,081

A1iso____+0,040____+0,040____+0,040____+0,040____+0,040____+0,040____+0,040____+0,040

A2iso____-0,040_____-0,040____-0,040____-0,040_____-0,040____-0,040_____-0,040____-0,040

B________465,9_____465,5_____465,2_____465,5_____465,9_____465,5_____465,2_____465,5

dB_______0,7982____0,8914____0,8774____0,8456____0,8807____0,8801____0,7795____0,7183

Таблица 6. Углы падения лучей в АСО и ИСО экрана при разных углах направления движения установки со скоростью Vss=300 км/с для Alfa1=+90,01 и Alfa2= +0,01 и получающиеся при этом ширина полос B и их смещение dB в долях B.

___________0________45_______90_______135_______180______225_______270_______315

A1aso____+0,020____-0,061____-0,077____+0,060____+0,020____-0,020_____-0,021____-0,037

A2aso____-0,020____+0,021____-0,037____+0,020____-0,020____-0,060_____-0,061____-0,077

A1iso____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020

A2iso____-0,020_____-0,020____-0,020____-0,020_____-0,020____-0,020_____-0,020____-0,020

B________932,4_____931,1_____929,7_____931,1_____932,4_____931,1______931,1_____929,7

dB_______0,3960____0,4454____0,4422____0,4226____0,4369____0,4401____0,3589____0,3932

Таблица 7. Углы падения лучей в АСО и ИСО экрана при разных углах направления движения установки со скоростью Vss=300 км/с для Alfa1=+90,01 и Alfa2= +0,01 и получающиеся при этом ширина полос B и их смещение dB в долях B.

___________0________45_______90_______135_______180______225_______270_______315

A1aso____+0,020____+0,061____+0,077____+0,061____+0,020____-0,021_____-0,037____-0,021

A2aso____-0,060____+0,101____+0,117____+0,101____-0,060____+0,019_____+0,003____+0,019

A1iso____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020____+0,020

A2iso____+0,060____+0,060____+0,060____+0,060____+0,060____+0,060____+0,060____+0,060

B________929,7_____931,1_____932,4______931,1_____929,7_____931,1_____932,4_____931,1

dB_______0,3657____0,4333____0,4554____0,4359____0,4429____0,4533____0,4070____0,3472

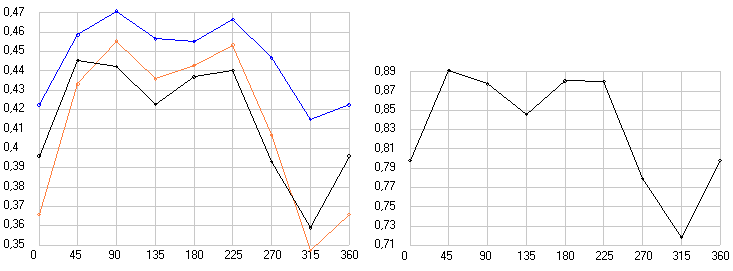
Рис. 27. График смещения полос со стеклянными пластинами толщиной 12,5 мм при разном направлении движения Земли с абсолютной скоростью Vss= 300 км/с. Черные графики - обычные полосы. На левом рисунке при B= 931 мкм (таблица 6, Alfa1=90,01 и Alfa2= +0,01), а на правом при B= 465 мкм (таблица 5, Alfa1=90,02 и Alfa2= +0,02). Цветные графики - составные полосы. Синий график при B= 1862 мкм (таблица 4, Alfa1=90,01 и Alfa2= -0,02), а красный график при B= 931 мкм (таблица 7, Alfa1=90,01 и Alfa2= -0,03). Графики построены с использованием программы Grafik4.

Как мы видим, даже при том, что при разных углах направления движения установки у нас получаются углы падения лучей в АСО то одного знака, то разных знаков, но после приведения составляющих скорости лучей к ИСО экрана у нас получаются все время углы падения лучей не только одного знака, который будет у лучей в покоящейся установке, но и по величине эти углы падения будут все время оставаться одни и те же и поэтому ширина полос должна оставаться неизменной. Правда, здесь я вынужден заметить, что полученные мною расчетные значения ширины полос при разных углах скорости установки хоть и незначительно, но отличались от какого то среднего значения и такие же значения отклонений получались и по моим формулам (5-4) и (5-5), но с другими отклонениями, хотя их величина находится в тех же интервалах. С чем это связано я пока точно сказать затрудняюсь, хотя здесь напрашивается простейший ответ, что это объясняется численным решением системы уравнений математической модели установки с каким то шагом по времени.

Конкретно я задавал при проведении этих вычислительных экспериментов основной шаг решения 1*10^-15 с, что при скорости света 300000 км/с даст путь пройденный лучами за один шаг решения 0,46 длинны волны света. Но при приближении к поверхностям стеклянных пластин, зеркал и экрана я уменьшал этот шаг решения в 1000 раз и, следовательно, погрешность определения координат точек падения центров лучей на эти поверхности и координат краев фронтов волн при определении эффективных углов наклона этих поверхностей составляла всего-навсего 0,00046 * 650 нм= 0,3 нм. Но эта погрешность при определении эффективных углов наклона по разнице координат падения на поверхность центра луча и края фронта волны у нас может вылиться в заметную величину, т.к. при такой ошибке в определении самого угла у нас отклонение луча при его падении на поверхность, находящуюся на расстоянии в несколько метров или десятков метров, будет значительно больше.

Но эти погрешности не помешают нам сейчас сделать качественный анализ полученных данных, т.к., например, для полос шириной 465 мкм, где среднее значение будет 465,525 мкм у меня максимальные отклонения расчетных значений ширины полос получаются +/- 0,35 мкм = 350 нм. А, эти 0,35 мкм составляют всего-навсего 0,075% от ширины полосы, хотя в некоторых расчетах и они могут сыграть свою роль. Поэтому, кому нужны будут более точные значения я рекомендую использовать более мелкий шаг решения, но при этом не забывайте, что в этом случае значительно увеличится время вычислений и могут начать проявлять себя погрешности от округления цифр в последнем знаке. Ведь программа Maikelson1 написана мною на языке программирования Visual Basic 6.0, а у него числовой тип данных Double имеет только 15-ть значащих цифр.

А простейший анализ полученных данных говорит о том, что при любых углах наклона зеркал мы качественно получаем идентичную картину изменения смещения полос при разных углах движения установки. А количественно эти данные отличаются использованием для расчета смещения полос их разной ширины, т.к. при одной и той же разности координат точек, куда будут падать два луча на экране, в метрах у нас эта разность координат будет разной в долях ширины полос, если полосы имеют разную ширину. Например, у нас полосы шириной 931 мкм будут в два раза шире полос шириной 465 мкм, а полосы шириной 1862 мкм будут в четыре раза шире полос шириной 465 мкм, а отсюда у нас и разные значения смещения полос в долях ширины полос при разной их ширине. Очевидно, что точно также и величина смещения полос зависящая от скорости поворота установки, т.е. величина полнопериодического эффекта, тоже будет зависеть от ширины наблюдаемых полос, что подтверждается данными Миллера на правом рис. 4.

Однако в смещение обычных полос и составных есть и некоторое отличие. Если мы рассмотрим обычные полосы (таблицы 5 и 6), то у нас максимальная разность положения полос будет 0,8914 - 0,7183= 0,1731 при ширине полос 465 мкм и 0,4454 - 0,3589= 0,0865 при ширине полос 931 мкм, т.е. во втором случае разность положений полос в долях их ширины будет в два раза меньше, чем в первом случае, т.к. ширина полос будет в этом случае в два раза больше. И точно также у составных полос разность положений будет 0,4554 - 0,3472= 0,1082 при ширине полос 931 мкм и 0,4709 - 0,4149= 0,056 при ширине полос 1862 мкм. Таким образом, при одинаковой ширине обычных и составных полос 931 мкм, мы получаем разные значения интервалов, где наблюдаются смещения полос. Обычные полосы имеют интервал 0,0865 ширины полос, а составные полосы интервал 0,056 ширины полос. А вот с чем это связано я пока не имею даже предположений. Да, многие исследователи писали, что у них иногда изменялась ширина полос прямо во время вращения прибора, а у меня в вычислительных экспериментах этого не может быть.

Но здесь для нас пока важно просто знать, что различия при наблюдении обычных полос и составных все же есть, а какие полосы они наблюдали не столь важно, т.к. мы все равно не знаем какая была ширина полос у всех исследователей, которые проводили натурные эксперименты на установках по схеме Майкельсона. Единственное, что мы можем сказать определенно, так это то, что, наблюдаемые ими значения смещения полос, вполне возможны при рассмотренных нами углах наклона зеркал или в случае отсутствия наклона у зеркал, но наклона полупрозрачной пластины на угол отличный от 135 градусов, если абсолютная скорость Земли, т.е. при ее движении сквозь неподвижный эфир, в котором распространяется свет, составляет сотни километров в секунду. А заодно мы можем по этим данным и подтвердить мое утверждение, что методика расчета начальных фаз двух лучей, которая излагается в учебниках, т.е. по разности времени движения двух лучей от источника света до экрана, является ошибочной, т.к. согласно данным таблицы 8 мы при этом должны были наблюдать в натурных экспериментах смещение полос согласно значениям dN(t) не на сотые доли их ширины, а на десятки полос.

Таблица 8. Разность начальных фаз двух лучей (в колебаниях света) полученная в вычислительных экспериментах данные которых отражены в таблицах 4, 5, 6 и 7, если ее определять по разности времени движения двух лучей от источника до экрана dN(t) и по разности времени движения зайчиков напряженности от координат падения двух лучей на экран по оси Х до точки с произвольной координатой dN(x), где для примера взята точка в середине экрана.

___________0________45_______90_______135_______180______225_______270_______315

dN(t)_4___-18,01____+3,622____+22,35____+3,500____-18,02____-5,710_____+9,500_____-5,580

dN(t)_5___+0,676____-0,433____+8,889____-0,517____+0,733____+35,79_____+60,38____+35,83

dN(t)_6___-8,169____-0,154____+12,93_____-0,271____-8,146____+17,84_____+17,92____+38,70

dN(t)_7___-16,81____+9,380____+27,94____+9,250____-16,84____-9,060______+4,270____-8,920

dN(x)_4___+4,563____+4,526____+4,514____+4,528____+4,529____+4,520_____+4,538____+4,569

dN(x)_5___+8,799____+8,892____+8,878____+8,845____+8,879____+8,879_____+8,779____+8,719

dN(x)_6___+4,397____+4,446____+4,442____+4,423____+4,437____+4,440_____+4,360____+4,393

dN(x)_7___+13,62____+13,55____+13,53____+13,55____+13,54____+13,53_____+13,58____+13,64

А, как я уже писал, кроме расчета dN(t) и dN(x) у меня в программе ведется и расчет N20-N10, где N20 и N10 это количество колебаний света в лучах от момента вылета лучей из источника света до момента касания ими экрана, которое получается суммированием количества колебаний света на каждом шаге решения уравнений. Но, т.к. в этих вычислительных экспериментах я не учитывал эффект Доплера, то у меня значения dN(t) и N20-N10 совпали. А, если учитывать эффект Доплера, то полученные значения N20 и N10 возможно, что будут и другие, а они нужны для расчета начальных фаз по моей 3-ей методике. А кроме того, наличие эффекта Доплера теоретически может объяснить постоянное смещение полос в одну сторону даже при покоящейся установке. Но, как я уже писал выше, быстрее всего, это объясняется нагревом зеркал, т.к., когда я убрал лампу из под установки Майкельсона [24], у меня это смещение практически прекратилось. Поэтому делать окончательные выводы, исходя из полученных мною данных в таблицах 4, 5, 6 и 7 и данных, которые наблюдались в натурных экспериментах, я считаю пока преждевременным. Но вот еще один вывод по данным вычислительных экспериментов мы можем сделать. Для этого давайте выполним еще две серии вычислительных экспериментов, например, с углами наклона зеркал Alfa1=+90,01 и Alfa2= -0,02 и получившиеся смещения полос отразим на рис. 28. Здесь мы будем изменять угол скорости движения только Земли со скоростью Vz= 30 км/с, а скорость всей солнечной системы Vss=300 км/с будем всегда задавать в одном направлении. На левом графике эта скорость будет направлена вдоль оси X, а на правом графике вдоль оси Y.

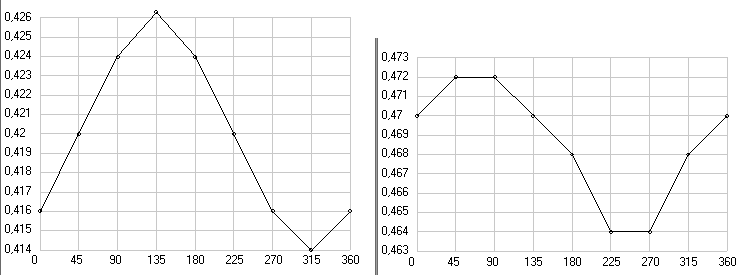
Рис. 28. Графики смещения полос при движении установки со скоростью Земли Vz= 30 км/с при разных углах направления движения Alfa(Vz) и со скоростью Солнечной системы Vss=300 км/с в горизонтальном направлении Alfa(Vss)=0 слева и в вертикальном направлении Alfa(Vss)= 90 справа.

А здесь в отличие от графика на рис. 26, где относительные смещения полос были +/-0,002, мы видим, что относительные смещения полос стали значительно больше и составляют на левом графике +/- 0,006 ширины полосы и на правом графике +/- 0,004 ширины полосы, т.е. в среднем +/- 0,005 ширины полосы. Т.е. мы можем сделать вывод о том, что при том же изменении скорости установки в разных направлениях на величину Vz= 30 км/с у нас при учете еще и постоянного направления движения всей Солнечной системы, интерферометр Майкельсона становится более чувствительным. А полученный нами средний результат +/- 0,005 ширины полосы вполне сопоставим с экспериментальными данными всех, кто проводил натурные эксперименты на установке Майкельсона. Более того, например, Миллер, именно такие эксперименты и проводил в конце своего исследования, когда он измерял смещение полос в разное время года, где скорость Земли изменяла свое направление, а направление скорости Солнечной системы не изменялось. И по этим данным, где у него смещения достигали 0,005 ширины полосы, он пытался определить направление в котором движется вся Солнечная система. Правда у него длина плеч интерферометра была по 32 м, а у меня в вычислительных экспериментах она задавалась 11 м, но здесь надо учитывать, что у меня скорости Vss и Vz задавались в одной плоскости, а, если они будут в разных плоскостях, как это и предполагал Миллер, то результаты будут совсем другие.

При этом, конечно же, гораздо проще выполнить эксперименты с поворотом установки при каком то одном положение Земли в произвольный момент времени, но желательно в 12 часов дня и когда у нас плоскость установки будет совпадать с плоскостью эклиптики, чтобы при повороте установки скорость Земли Vz была в плоскости установки. И при этом у нас будет изменяться не только угол направления движения Земли со скоростью Vz, но будет изменяться и угол под которым будет двигаться вся солнечная Система со скоростью Vss. Вот только лично я, хоть и немного экспериментировал с установкой Майкельсона, но сделал для себя вывод о том, что она очень плохо подходит для определения абсолютной скорости Земли. Поэтому никаких количественных выводов по полученным нами сейчас данным я делать не буду. К тому же, при проведении этих вычислительных экспериментов я совершенно не учитывал эффект Доплера, который обязательно должен повлиять на результат. И поэтому пока можно сделать только качественный вывод о том, что движение установки вместе с Землей сквозь неподвижный эфир должно приводить к смещению полос и это подтверждается данными многочисленных исследователей, проводивших натурные эксперименты на установке Майкельсона.

5. Исследования выполненные на установке Юдина

Прежде, чем приступить к проведению натурных экспериментов на установке своей конструкции, я первым делом измерил величину одного пикселя в вэбкамерах и коэффициент увеличения изображения объективом кинопроектора Луч2, который я использовал в некоторых экспериментах. Наклеив прозрачную пленку с сеткой 0,1*0,1 мм на объектив кинопроектора, я освещал его лучом лазера и на экране, который располагал на разных расстояниях от объектива, замерял размер получающегося расстояния между линиями сетки. После того, как получился график линейной зависимости, я нашел, что каждый метр расстояния между объективом и экраном дает увеличение изображения примерно в 48 раз. Аналогично я наклеил эту пленку на вэбкамеры перед матрицами, удалив при этом оптику вэбкамер, и определил, что в вэбкамере с размером матрицы 640*480 пикселей размер одного пикселя составляет 2,2 мкм, а в вэбкамере с размером матрицы 1920*1080 пикселей размер одного пикселя составляет 3,0 мкм. Теперь надо было определить на сколько точно я смогу фиксировать смещения интерференционных полос с таким оборудованием. Для этого я собрал свою установку (см. рис. 29)

в гараже, где максимально удлинил основной брус, чтобы иметь максимальное расстояние как от зеркал до объектива кинопроектора, так и от него до вэбкамеры.

Рис. 29. Общий вид установки собранной по схеме "b" слева и полосы, видимые на бумажном экране, установленном за объективом кинопроектора, справа.

При этом, т.к. у меня не получалось при стандартной схеме установки (схема "a" на рис. 13) пододвинуть зеркала очень близко к треугольной призме, чтобы получить очень маленькие углы падения лучей на экран и таким образом максимально широкие обычные полосы, я собрал свою установку по схеме "b", которая позволяет получить очень широкие составные полосы, т.к. разница в углах падения лучей на экран может быть очень маленькой. И как мы видим на мониторе ноутбюука, который на левом рис. 29 находится в самом конце бруса, а перед ним расположен объектив кинопроектора с ширмой, у нас на экране хорошо видны две полосы. А, если еще отодвинуть вэбкамеру от объектива кинопроектора на то место, где находится сейчас ноутбук, то одна полоса займет весь экран по ширине. Таким образом, с использованием примененного мною оборудования мы можем уверенно фиксировать смещения полос даже на тысячные доли их ширины, т.к. это будет минимум 2 пикселя на мониторе, который по ширине имеет размер тоже 1920 пикселей, как и 2-я вэбкамера. А, если в такой схеме не использовать вэбкамеру, то составные полосы будет отлично видно и на экране, если его расположить на расстоянии примерно 20 см от объектива, как это видно на правом рис. 29. А для более детального рассмотрения установки в этом эксперименте можете просмотреть видеофайл [29].

После этого я поместил установку в подвале дома, где температура была более стабильная, и убрал удлинительный брус, чтобы установка могла вращаться на подвеске. И первым делом я, конечно же, проверил насколько получающиеся у меня полосы стабильные и не смещаются ли они постоянно в одну сторону, как это было у всех, кто проводил натурные эксперименты на установке Майкельсона. И, как я уже писал, в нескольких экспериментах с неподвижной установкой, собранной по классической схеме "а", которые длились часами или сутками и при этом велась запись в файл изображения с вэбкамеры, например, вот в этом видиофайле [22], я не обнаружил устойчивого движения полос в одну сторону при покоящейся установке. В начале записи с 12 часов дня до вечера полосы сместились на одну их ширину влево, а потом до утра следующего дня еще на 1,5 полосы влево, но к полудню суммарное смещение стало только 2 полосы, а к вечеру суммарное смещение уменьшилось до одной полосы. При этом, как видно в видеофайле, температура колебалась в интервале примерно от 6,1 градуса до 6,4 градуса, но очень не равномерно. Поэтому, чтобы выявить явное влияние температуры в помещение на смещение полос, я записал видеофайл [30], где в начале записи я приоткрыл дверь в подвал и за два часа температура в подвале упала на 1 градус и полосы сместились на 7 полос влево, а потом я закрыл дверь в подвал и включил обогреватель. За два часа температура увеличилась на 3,5 градуса, а полосы сместились на 17,5 полос вправо и при этом деформация в креплениях зеркал произошла такая, что даже ухудшилось качество интерференционной картинки. Таким образом, я выяснил, что даже незначительное изменение температуры при проведение серии экспериментов, которая может длиться часами, может привести к заметным ошибкам в экспериментальных данных. А поддерживать стабильной температуру в подвале с точностью до десятых или сотых долей градуса я в своих условиях не могу и поэтому проведение в моих условиях длительных экспериментов отпадает.

Но, если проводить эксперименты, которые длятся несколько минут, то никаких заметных смещений полос от изменения температуры не должно быть и я выполнил эксперимент с медленным поворотом своей установки на подвесе, который крепился к бревну на потолке (см. видеофайл [31]). Вот только при этом у меня наблюдалось не только дрожание полос, но и очень заметный полнопериодический эффект, т.е. смещение полос в одну сторону при повороте установки против часовой стрелки и потом в другую сторону при ее повороте по часовой стрелке. Поэтому ни о какой фиксации положения полос, вызванного ориентацией прибора в пространстве, с точностью до сотых долей ширины полос, чтобы с уверенностью сказать, что мой интерферометр реагирует на положение установки в пространстве, не могло быть и речи. Тогда я задумался о том как вообще заставить полосы смещаться на теоретически рассчитанную величину, чтобы можно было четко зафиксировать смещение полос и по этому смещению проверить правильность расчета начальных фаз двух лучей по предложенной мною 3-ей методике и по методике излагаемой в учебниках. Для этого я решил на пути одного из лучей установить цилиндр со стеклянными крышками, в котором можно будет изменять давление воздуха и, следовательно, будет изменяться его оптическая плотность, а это должно привести к тому, что должно изменяться время движения этого луча до экрана. Простейший расчет дает увеличение оптической плотности воздуха со значения n0=1,0003 до n=1,00042 при увеличении согласно зависимости (6) давления воздуха на 0,4 атм или на 300 мм ртутного столба от нормального атмосферного давления p0=760 мм.рт.ст. Теперь рассчитаем разность времени движения второго луча внутри цилиндра длиной 0,1 м, когда у нас давление в нем будет 760 мм.рт.ст. и 1060 мм.рт.ст., определив при этом скорость света в этих двух вариантах расчета с разной оптической плотностью воздуха.

n-1= (n0-1)*p/p0 (6)

V0= Vs0*1/n0= 299,910*10^6 м/с

V300= Vs0*1/n= 299,874*10^6 м/с

T0= 0,1 / V0= 3,33433*10^-10 с

T300= 0,1 / V300= 3,33473*10^-10 с

dT= 4*10^-14 с

Следовательно, за время dT у нас второй луч, двигаясь к экрану, при избыточном давление в цилиндре 300 мм.рт.ст. сделает при частоте лазера v0=4,615*10^14 Гц на 18,5 периодов колебаний больше, чем при его движении до экрана при стандартном давлении. Естественно, что при избыточном давлении 100 мм.рт.ст., когда его оптическая плотность будет 1,00034 он сделает на 6,2 периода больше и для того, чтобы полосы сместились на 0,3 их ширины, нам надо задать оптическую плотность воздуха n= n0 + 1,2*10^-4 / 18,5 / 3= n0 + 2,2*10^-6= 1,000302. А что у меня получилось при проведении этого натурного эксперимента можно посмотреть в этом видеофайле [33]. Как и следовало ожидать, исходя из существующей методики расчета начальных фаз двух лучей, при поднятии давления до 110 мм.рт.ст. у нас происходило смещение на 6 полос, что примерно соответствует расчетному значению смещения на 6,2 полосы при избыточном давлении 100 мм.рт.ст. (более точные данные в этом тестовом эксперименте нас не интересуют и поэтому я вел расчет нужного давления по упрощенной формуле (6)).

Теперь давайте посмотрим, что у нас получается при расчете интерференционной картинки, когда разность начальных фаз после проведения вычислительных экспериментов при оптической плотности воздуха в цилиндре равной 1,000302, 1,000304 и 1,000306 будет 0,308, 0,615 и 0,923 периода. Для этого после проведения вычислительного эксперимента на математической модели интерферометра с этой плотностью воздуха в цилиндре перенесем данные с формы 4 программы Maikelson1 на форму 3 (для этого надо нажать кнопку "Перенести данные на форму расчета интерференции"). Но здесь я вынужден заметить, что я, изготавливая цилиндр длиной 10 см, не предусмотрел, что при этом правое зеркало, если цилиндр разместить между призмой и зеркалом, будет очень далеко находится от призмы и у нас при таком угле падения получатся очень узкие полосы, которые потом будет трудно наблюдать. А код программы был уже написан под размещение цилиндра именно в этом месте. Поэтому мне пришлось в этих первых экспериментах с цилиндром разместить его на пути 2-го луча от 2-го зеркала до экрана, как это отражено на рис. 30, и при этом в вычислительных экспериментах я не стал учитывать ни аберрацию, ни изменение эффективного угла наклона зеркал, ни эффект Доплера, а учел только влияние оптической плотности на скорость света в цилиндре и принял, что установка покоится в АСО.

Рис. 30. Общий вид моей установки, собранной по схеме "а", когда на пути 2-го луча от зеркала до объектива кинопроектора установлен цилиндр, где можно изменять давление воздуха.

А в этом случае нас будет интересовать только разность времени движения двух лучей до экрана и поэтому я выполнил вычислительные эксперименты с несколькими расстояниями от призмы до зеркал. С реальными расстояниями, но без цилиндра, чтобы убедится в правильности расчета ширины полос (у меня получилось расчетное значение Bmod=5,0 мкм, а наблюдаемое в натурном эксперименте с учетом увеличения объективом кинопроектора было Bnab=5,6 мкм, как это отражено на левом рис. 31, т.е. тут мы опять получаем, как и в таблице 3, Bmod/Bnab=0,89) и с произвольным расстоянием до правого зеркала, которое будет таким, чтобы между призмой и зеркалом уместился цилиндр, который позволит нам определить разность времени движения лучей до экрана при изменении давления воздуха в цилиндре. А при отсутствии эффекта Доплера он позволит рассчитать разность количества колебаний, сделанных светом, при его движение в цилиндре с разной оптической плотностью. Да, во втором вычислительном эксперименте будет получатся расчетная ширина полос отличная от тех, что были в натурном эксперименте, но нас в этих экспериментах интересует только смещение полос в долях их ширины, а оно в этом случае не должно зависеть от ширины полос, как это было на графиках рис. 27, т.к. при этом координата точки падения 2-го луча на экран не должна изменяться. И теперь, если мы не будем в расчетах учитывать тот факт, что два луча света не одновременно пришли к экрану, то мы с использованием 1-ой и 2-ой методик определения начальных фаз двух лучей, получим картинки, отражены на рис. 32, где смещение полос будет соответственно -0,304, -0,616 и -0,920 их ширины, т.е. расчетное значение будет хорошо соответствовать данным полученным в натурном эксперименте.

Рис. 31. Интерференционные полосы наблюдаемые на экране ноутбука при использовании вэбкамеры 640*460. Слева при установке на пути лучей на расстоянии 0,945 м от призмы объектива кинопроектора и потом вэбкамеры на расстоянии 0,89 м от объектива, как это изображено на рис. 30, где объектив увеличивал изображение в 47,2 раза. Справа при использовании только вэбкамеры, установленной на расстоянии 1,835 м от призмы, т.е. без увеличения изображения объективом кинопроектора.

Рис. 32. Положение интерференционных полос при разной начальной разности фаз, определяемой по 1-ой или 2-ой методикам. На верхнем рисунке при разности фаз 0, пониже при разности фаз 0,308 и еще ниже при разности фаз 0,615. А на самом нижнем рисунке отображено изменение со временем напряженности поля двух лучей в разных местах экрана для одного момента времени при разности фаз 0,615, которая в разных точках экрана постоянно меняется, т.к. красная синусоида первого луча движется вправо, а синяя синусоида второго луча движется влево. Скриншот программы Maikelson1.

А вот при использовании предложенной мною 3-ей методики, которую мы использовали в рассмотренных выше экспериментах на установке Майкельсона, никакого смещения полос при моделировании этого эксперимента почему то не происходило, что меня озадачило. Ведь, как я уже писал выше, чтобы оба фронта волны света, вылетевших из лазера, коснулись экрана одновременно, т.к. только в этом случае эти два луча смогут одновременно воздействовать, например, на центральную точку экрана, где мы будем вычислять суммарную напряженность поля и как следствие освещенность экрана в этой точке, у нас фронт волны первого луча должен вылететь из лазера в момент времени Т01= dT, т.е. надо использовать предложенную мною 3-ю методику расчета начальных фаз. При этом не спасает ситуацию даже то, что при отражении света от более плотных оптических сред фаза луча изменяется на 180 градусов, т.к., во-первых, если у меня будет по одному отражению, то в том же месте на экране встретятся не минимумы напряженностей, а максимумы напряженности, т.е. все равно будет образовываться светлая полоска, а, во-вторых, у меня происходит по два отражения обоих лучей (от граней призмы и от зеркал) и поэтому их фазы не должны изменяться.

Первоначально я настолько был обескуражен таким неожиданным результатом, что допустил возможность даже того, что при движении в более плотной оптической среде свет уменьшает не свою скорость, а свою частоту, т.к. такой вариант позволял по 3-ей методике получить нужное смещение полос. И, как напоминание об этом, у меня в программе осталась возможность при моделировании выполнить именно такие превращения со светом, которые приводят к тому, что в более плотных оптических средах уменьшается частота света, а не его скорость. Однако, понимая, что этот вариант пока все таки является искусственным, а меня интересует не только результат, но и физика наблюдаемых явлений, я начал поиск возможного выхода из создавшейся ситуации. Напоминаю, что при изложении теории интерференции я изложил три методики расчета начальных фаз двух лучей для использования их в формулах (4-1) для расчета их конечных фаз в произвольной точке экрана, когда я фазу света в лучах, падающих на экран, определял по количеству периодов колебаний света сделанных за время движения лучей от источника до экрана.

И тут я взглянул на этот процесс немного с другой стороны. Если принять, что в момент времени Т=0, когда фронт второго луча вылетел из лазера, его фаза была равно нулю, т.е. N2=0, а в момент времени Т2 именно этот фронт волны с этой фазой и добрался до экрана, то, чтобы фронт волны первого луча упал одновременно с ним на экран, он должен вылететь в момент времени dT, когда его фаза будет N1= v0*dT. Поэтому я сейчас добавлю к рассмотренным выше трем методикам еще две методики 4-ю и 5-ю. Здесь N10 и N20 это количество колебаний света в лучах, за время их движения Т1 и Т2 от источника до экрана, которое вычисляется суммированием колебаний сделанных на каждом шаге решения уравнений математической модели установки. Но, если у нас не учитывается эффект Доплера, то эти значения можно вычислить и по времени движения лучей от источника до экрана, т.е. по 2-ой методике, т.к. при этом принимается, что частота на всех этапах пути лучей не изменяется и равна частоте источника v0. При этом у меня принято, что dT всегда равно T2-T1.

1. N1=N10, N2=N20

2. N1=v0*T1, N2=v0*T2

3. N1=N10+v0*dT, N2=N20

4. N1=v0*dT, N2=0

5. N1=N10 - v0*T1 + v0*dT, N2=N20 - v0*T2

Моделирование интерференционной картины с использованием 4-ой методики показало (см. таблицу 9, где dN разность начальных фаз двух лучей), что смещения полос dB (дано в скобках) при этом получаются практически такие же, как и в приведенном выше расчете, когда мы использовали значения фаз N1=N10 и N2=N20, но полосы при этом смещаются в другую сторону. У меня программа всегда находит положение полосы на экране в интервале от нуля до 1-ой полосы и поэтому всегда выдает положительные значения положения полосы в долях ширины полосы, а потом, зная положение полосы в исходном положении, я уже нахожу само смещение полосы, которое привожу в скобках. А выяснение того, в какую же сторону на самом деле смещаются полосы, заставило меня провести дополнительный эксперимент, т.к. я просто запутался где у меня в этом натурном эксперименте смещение полос влево, а где вправо.

Таблица 9. Расчетные значения смещения полос в покоящейся установке от исходного положения, т.е. при оптической плотности воздуха 1,0003, при изменение оптической плотности воздуха в цилиндре до значений 1,000302, 1,000304 и 1,000306, когда расчет начальных фаз двух лучей ведется по 1-ой методике и по 4-ой.

оптическая_________N1=N10, N2=N20_______N1=v0*dT, N2=0

плотность_______dN_________dB____________dN______dB

1,000302_______0,308____0,696 (-0,304)_____-0,308____0,312

1,000304_______0,615____0,384 (-0,616)_____-0,625____0,620

1,000306_______0,923____0,080 (-0,920)_____-0,923____0,928

Дело в том, что в стандартной вэбкамере в ее оптике происходит поворот изображения на 180 градусов поэтому в программе ContaCam, которую я использовал для визуализации изображения, есть даже опция разворота изображения на 180 градусов, а я не зафиксировал была она у меня включена или нет. К тому же я в вэбкамере вынул оптику и теперь сомневаюсь как там происходит трансформация изображения с матрицы вэбкамеры. А кроме того оптика кинопроектора тоже разворачивает изображение на 180 градусов и поэтому я решил упростить задачу, т.е. убрать оптику кинопроектора и направить лучи от зеркал сразу на матрицу вэбкамеры. При этом мне пришлось и немного пододвинуть зеркала к треугольной призме, чтобы сделать поменьше углы падения лучей на экран. И хотя ширина полос даже в этом случае получилась очень маленькой (18,3 мкм), но это гораздо лучше чем было на объективе кинопроектора (5,6 мкм), когда я проводил первый эксперимент. Но там у меня оптика кинопроектора давала их 48-и кратное увеличение на каждый метр расстояния от объектива кинопроектора до вэбкамеры и поэтому, как видно в видеофайле [33] и на левом рис. 31 полосы наблюдались очень хорошо, т.к. их ширина на матрице вэбкамеры была 238,5 мкм, что не сравнимо с 18,3 мкм, которые мы видим на правом рис. 31, когда не используется увеличение изображения объективом кинопроектора.

Как показал этот эксперимент, полосы тоже смещались на 6 полос при давлении 110 мм.рт.ст. и смещались так же влево, но теперь я точно знал, где у меня левая сторона, а где правая, потому что я просто поднес линейку к матрице вэбкамеры сверху, и увидел ее тень на мониторе сверху, а, поднося линейку к матрице вэбкамеры слева, я видел ее тень на мониторе справа. Таким образом, учитывая то, что матрица, которая как бы смотрит на лучи, которые летят к ней, выдает изображение, как и фотоаппарат, такое, что правая рука человека находится на фотографии слева, то это означает, что в нашем эксперименте при взгляде на матрицу (экран) со стороны падающих лучей это будет означать, что реально по экрану полосы смещались вправо. А это доказывает, что правильным при расчете интерференционной картины является определение начальных фаз двух лучей падающих на экран по 4-ой методике, а не по 1-ой. Если кому-то интересно, то можете посмотреть изображение с вэбкамеры и этого эксперимента в конце видеофайла [33], где я после того, как полосы успокоятся, два раза подымаю давление в цилиндре до 110 мм.рт.ст. и потом сбрасываю его до нуля. При этом обращаю ваше внимание на то, что результаты полученные нами выше при использовании 3-ей методики в вычислительных экспериментах на установке Майкельсона, остаются в силе, т.к. там у нас оба луча двигались одинаковое время в более плотной оптической среде, т.е. в стеклах, и поэтому это не привело к ошибке расчета смещения полос.

Но мне все таки не давало покоя то, что я в этих экспериментах с цилиндром помещал его в натурных экспериментах в одном месте, а при моделировании в другом, хотя, вроде бы это не должно было отразиться на результатах, т.к. я рассматривал движение света в покоящейся установке, а, следовательно, никаких физических эффектов, кроме изменения скорости света в цилиндре, при этом не должно быть. К тому же я хотел и убедится в том, что при увеличении давления в цилиндре, полосы на экране в натурном эксперименте будут смещаться именно вправо. Поэтому я изготовил и более короткий цилиндр длиною 5 см и поместил его, как в натурных экспериментах, так и в вычислительных между призмой и вторым зеркалом, в двух вариантах конструкции моей установки (собранной по схеме "а" и по схеме "с"). По классической схеме "а" я задал расстояние от треугольной призмы до левого зеркала 3 см, а до правого 11 см, что в принятых мною обозначениях запишется как m3p11_338, где 338 это расстояние от призмы до экрана, но, если установлен еще и объектив кинопроектора, то эта цифра будет отражать расстояние до него, а следующая цифра (если она будет) это будет расстояние от объектива до экрана (матрицы вэбкамеры). А установка собранная по схеме "с", где левая половина луча от лазера не отражается на призме к зеркалу 1, а пролетает мимо призмы к экрану, будет иметь обозначение m0p11_338. Но, если луч, пролетевший мимо призмы, потом будет отражен дополнительным зеркалом (или дополнительной призмой) вправо, куда мы поместим левое зеркало 1, т.е. мы будем иметь установку собранную по схеме "b", то такая установка при расстоянии от призмы до зеркала 1 равном 3 см получит обозначение p3p11_338.

При моделировании движения правого луча света через камеру длиною 5 см с изменяемым давлением воздуха в ней я задавал оптическую плотность воздуха не только соответствующую атмосферному давлению, т.е. 1,0003, но и 1,000304 и 1,000308, что согласно расчету, приводившемуся мною выше, в натурном эксперименте должно было приводить к смещению полос на 0,3 их ширины и на 0,6 их ширины. Напоминаю, что при использовании мною ранее камеры длиной 0,1 м я для того, чтобы получить такие смещения полос, задавал давление воздуха в камере, которое соответствовало оптической плотности воздуха 1,000302 и 1,000304. Полученные при моделировании результаты по смещению полос в двух экспериментах, где не используется объектив кинопроектора, я привожу в таблицах 10 и 11, где у меня строки пронумерованы согласно вариантам расчета начальных фаз двух лучей, а в колонках приведены в числителе экспериментальные данные расчета разности этих фаз, т.е. N2-N1 для центральной точки на экране, а в знаменателе получающиеся значения положения полосы при различной оптической плотности воздуха внутри камеры цилиндра. И далее в скобках у меня приводятся значения смещения полос dB при плотности 1,000304 и 1,000308 от положения полосы которое было при плотности 1,0003. При этом я привожу и данные, которые получаются по 5-ой методике, т.к. при моделировании я задал скорость Vz= 30 км/с, с которой установка движется в вертикальном направлении. Поэтому мне пришлось учитывать все физические эффекты, которые будут при этом наблюдаться, т.е. и аберрацию, и эффективные углы наклона зеркал и эффект Доплера, а не только влияние оптической плотности воздуха в цилиндре на скорость света, как это было в вычислительных экспериментах в таблице 9.

Таблица 10. Расчетные значения смещения полос в движущейся установке от исходного положения, т.е. при оптической плотности воздуха 1,0003, в эксперименте m3p11_338 (схема "а") при изменение оптической плотности воздуха в цилиндре до значений 1,000304 и 1,000308, когда расчет начальных фаз двух лучей ведется по разным методикам.

__________1,0003_______________1,000304__________________1,000308

1___133191,79 / 0,202 (0)____133192,10 / 0,895 (-0,307)____133192,41 / 0,587 (-0,615)

2___133310,52 / 0,475 (0)____133310,83 / 0,167 (-0,308)____133311,13 / 0,859 (-0,616)

3___-118,73 / 0,720 (0)_______-118,73 / 0,720 (0)__________-118,73 / 0,720 (0)

4__-133310,52 / 0,511 (0)____-133310,82 / 0,817 (0,306)____-133311,13 / 0,127 (0,616)

5__-133429,25 / 0,239 (0)____-133429,55 / 0,546 (0,307)____-133429,86 / 0,855 (0,616)

Таблица 11. Расчетные значения смещения полос в движущейся установке от исходного положения, т.е. при оптической плотности воздуха 1,0003, в эксперименте m0p11_338 (схема "с") при изменение оптической плотности воздуха в цилиндре до значений 1,000304 и 1,000308, когда расчет начальных фаз двух лучей ведется по разным методикам.

__________1,0003_______________1,000304__________________1,000308

1___179721,10 / 0,892 (0)____179721,40 / 0,584 (-0,308)____179721,71 / 0,276 (-0,616)

2___179719,46 / 0,532 (0)____179719,76 / 0,226 (-0,306)____179720,07 / 0,917 (-0,615)

3___26,89 / 0,099 (0)________26,89 / 0,099 (0)____________26,89 / 0,099 (0)

4__-179668,96 / 0,943 (0)____-179669,26 / 0,251 (0,308)____-179669,57 / 0,558 (0,615)

5__-179667,31 / 0,302 (0)____-179667,62 / 0,611 (0,309)____-179667,93 / 0,917 (0,615)

А, чтобы вам было более понятно какие натурные эксперименты я проводил несколько дней с двумя вэбкамерами и с различными расстояниями от призмы до зеркал и от призмы до вэбкамеры или объектива кинопроектора, я на скорую руку выполнил четыре эксперимента с одной вэбкамерой и неизменным расстоянием между призмой и вэбкамерой 3,38 м (для этого мне пришлось опять установить удлинитель основного бруса), но в двух экспериментах я не использовал объектив кинопроектора, а в двух помещал объектива между призмой и вэбкамерой [34]. Сначала в файле идут два эксперимента с расстояниями от призмы до зеркал 3 и 11 см, а потом с расстояниями 0 и 11 см, т.е. в последнем случае левый луч не отражается от левого зеркала, а сразу после ребра призмы летит прямо к вэбкамере. Как натурные так и вычислительные эксперименты показали, что согласно методик 1 и 2 полосы, как и в покоящейся установке (см. таблицу 9), смещаются на 0,3 и 0,6 ширины полос влево, а согласно методике 3 опять не смещаются. А вот методика 5, так же, как и методика 4, показали смещение полос на 0,3 и 0,6 их ширины вправо. Но, т.к. здесь учитывается эффект Доплера, то даже из двух ошибочных методик 1 и 2 более правильной будет методика 1, а из двух методик 4 и 5, которые обе дают правильные значения смещений полос, т.е. вправо, более правильной является методика 5, т.к. 4-я методика не учитывает эффект Доплера, а поэтому применима только, если у нас на всем пути движения обоих лучей будет неизменная частота света в них. Но здесь обе методики дали одинаковые результаты, т.к. при движении моей установки вверх эффект Доплера для двух лучей будет симметричным.

Таким образом, если мы не учитываем эффект Доплера, то мы можем использовать для расчета начальных фаз и 4-ю и 5-ю методики, например, в вычислительных экспериментах с поворотом моей установки в различных направлениях, как я это делал в вычислительных экспериментах на математической модели установки Майкельсона (см. таблицы 4, 5, 6 и 7). И я выполнил такие вычислительные эксперименты на классической схеме моей установки "а", с размерами плеч по 3 см и расстоянием от треугольной призмы до экрана 80 см, что дало расчетные значения углов наклона зеркал Alfa1= 133,908315 и Alfa2= 46,091685 градусов, т.е. в принятых мною обозначениях это будет схема m3p3_80. При этом у меня получилось, что при скорости всей установки Vss=300 км/с, если не учитывать эффект Доплера и начальные фазы лучей рассчитывать по моей 3-ей методике, то полосы, согласно данным вычислительных экспериментов, практически не должны смещаться, а, если при этом начальные фазы лучей рассчитывать по моей 4-ой или 5-ой методикам, то мы получаем идеальные синусоиды (см. синюю кривую на рис. 33), которые отражают полупериодический эффект, который хотели зарегистрировать с использованием интерферометра Майкельсона.

Да, при этом и методики 1 и 2 (красная кривая) тоже дают такую же синусоиду, которая имеет зеркально противоположные знаки у смещений, но мы уже выяснили, что эти методики явно ошибочные, хотя и дают похожие на правду результаты. При этом, если увеличить плечи интерферометра в два раза, но так, чтобы углы падения остались примерно такие же (это надо, чтобы ширина полос оставалась неизменной), т.е. собрать ее по схеме m6p6_160, то мы получим смещения полос в два раза больше (в долях ширины полос). А конкретно схема m3p3_80 дает смещение полос +/- 0,046, а схема m6p6_160 дает +/- 0,092 ширины полосы при их ширине в обоих случаях B=8,6 мкм.

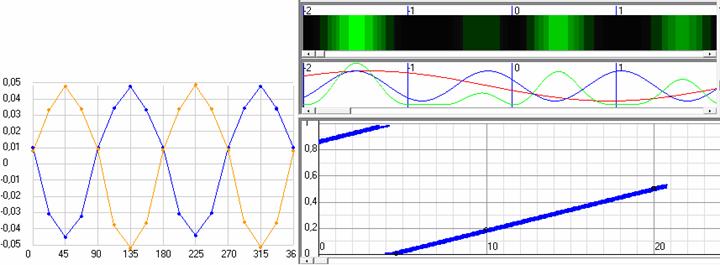
Рис. 33. Слева графики смещения полос при разном направлении движения Земли с абсолютной скоростью Vss= 300 км/с на установке собранной по схеме m3p3_80, где красная кривая получена при расчете начальных фаз по 1-ой и 2-ой методикам, а синяя по 4-ой и 5-ой методикам. Справа график смещения полос в вычислительном эксперименте m3p11_338 при определение начальных фаз двух лучей по 5-ой методике, где на графике масштаб времени 1*10^-12 с/см. Скриншот программы Maikelson1.

Кто то может опять сказать - а какая разница как определять фазы двух лучей (как говорят в учебниках или по предложенной мною методике), т.к. результат то именно по величине смещения полос получается один и тот же. На что я возражу, что я сейчас рассмотрел самые простейшие случаи расчета интерференционной картины по параметрам двух лучей падающих на экран, где или не учитывается эффект Доплера m3p3_80, или он учитывается при движении установки вверх m3p11_338 и m0p11_338, где эффект Доплера будет симметричным. А при разных направлениях у нас эффект Доплера должен по разному воздействовать на изменение частоты света в двух лучах и поэтому возможно, что в этом случае даже все испробованные мною методики окажутся не верными, а не только убогая 2-я методика изложенная в учебниках. Да, пока у меня получается, что при разной частоте лучей на разных участках их движения до экрана, надо определять их начальные фазы, т.е. для одного и того же момента времени, когда они падают на экран, при их расчете по 5-ой методике. Но проверить это не так просто, т.к. у меня пока остаются некоторые вопросы по моделированию эффекта Доплера при многократном отражении лучей света от движущихся поверхностей.

Например, на правом рис. 33 мы видим график изменения положения полос в вычислительном эксперименте m3p11_338 при определении начальных фаз двух лучей по 5-ой методике, т.е. здесь мы видим, что, если учесть эффект Доплера при построении интерференционной картинки, то получается, что полосы не должны стоять на месте. А конкретно на этом графике мы видим, что они сместились на пол полосы за время (20 - 4,5)*10^-12 = 15,5 *10^-12 с, а это при ширине полосы в этом эксперименте 15,58 мкм даст скорость 469 км/с, что для полос является просто огромной скоростью и поэтому в натурном эксперименте мы при такой скорости увидели бы засвеченным весь экран, т.е. не видели бы никаких полос. А происходит это смещение полос из-за разной частоты света двух лучей принятой экраном. У нас получилась частота света в 1-м луче v1/v0= 1,0000538, а во 2-м v2/v0= 0,9999846, т.е. получается, что я не правильно смоделировал эффект Доплера в математических моделях установок Майкельсона и своей, хотя я все делал вроде бы правильно. А конкретно я посылал к движущейся поверхности два фронта плоской волны разделенных заданным количеством периодов колебаний света, например, разделенных в АСО десятью длинами волн света, которые определял по известной частоте, и потом засекал время, когда левый и правый края двух фронтов коснутся этой поверхности. Затем я находил по этим значениям среднее время для первого и второго фронтов и их разность, а зная, что у меня за этот промежуток времени поверхность приняла 10-ть периодов колебаний света, я находил частоту света принятую этой поверхностью.

Аналогично я находил и частоту света отраженную движущимися поверхностями, а принятую фиктивным экраном покоящимся в АСО. При этом я не задавал опять 10-ть периодов колебаний отраженного луча света, а просто, когда концы фронтов волн касались движущихся поверхностей, я направлял движение этих краев фронтов в соответствие с законом отражения, т.е. принимал угол отражения равным углу падения, но при этом я использовал эффективные углы наклона движущихся поверхностей, а не статические. И теперь эту частоту, принятую фиктивным экраном, покоящимся в АСО, я считал частотой света движущегося от рассмотренной нами поверхности, где он отразился, до следующей движущейся поверхности и т.д. Например, на левом рис. 34 вы видите анимацию процесса моделирования эффекта Доплера при движении источника сигналов, т.е. лазера, в вертикальном направлении, где у нас два фронта волны (синие линии), вылетевших из лазера в моменты времени Т1=0 и T2=10/v0, т.е. после 10-ти колебаний света в лазере, который за это время сместился в вертикальном направлении на расстояние VYiso*T2, где VYiso скорость всей установки в АСО, летят к неподвижному в АСО приемнику (черная линия). И в моменты времени, когда края этих двух фронтов коснутся приемника, мы найдем среднее время прихода двух фронтов к приемнику, а потом, зная, что за этот промежуток времени приемник принял 10-ть периодов колебаний света, определим принятую им частоту, т.е. это будет частота света в лучах, которые летят в АСО к треугольной призме. А на анимации мы видим, что 1-ый фронт уже коснулся фиктивного приемника и продолжает двигаться дальше, а 2-ой фронт подлетает к приемнику.

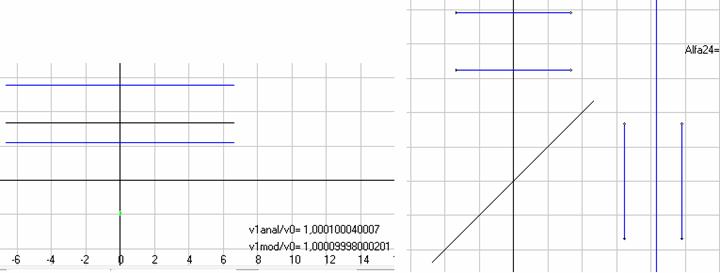
Рис. 34. Анимация моделирования эффекта Доплера для луча света движущегося на участке от лазера до треугольной призмы слева и на участке от правой грани призмы до правого зеркала справа. Скриншоты программы Maikelson1.

А на правом рис. 34 вы видите анимацию процесса моделирования эффекта Доплера при отражение луча света от правой грани призмы (черная наклонная линия), когда она вместе со всей установкой тоже движется в АСО вверх. Вверху вы видите две синие линии, которые являются двумя фронтами волн света летящих в АСО от лазера к грани призмы, а расстояние между ними равно 10-ти длинам волн этого света. Но в данный момент времени они уже отразились от правой грани призмы и летят вправо к неподвижному в АСО приемнику (вертикальная синяя линия), а на анимации они так и продолжают фиктивно (чисто информативно) двигаться еще и вверх. При этом мы видим, что 1-ый фронт уже коснулся приемника и мы засекли время, когда это произошло, а сейчас он на анимации просто для наглядности продолжает двигаться вправо. А второй фронт отраженный от поверхности призмы тоже движется вправо и на анимации подлетает к приемнику. И после фиксации времени, когда и он достигнет приемника, мы определим частоту света отраженного от правой грани движущейся вертикально призмы. А на приведенном ниже скриншоте программы Maikelson1 вы видите в середине рисунка табличку, где приводится получающаяся при моделировании частота света 1-го луча (слева) и 2-го луча (справа) данная в долях частоты лазера. При этом сначала идет частота света на конкретном участке пути, которые пронумерованы от 10 до 18 для 1го луча и от 20 до 28 для второго луча, а потом идет частота принятая в конце этого пути какой то поверхностью. А, чтобы вам было легче разобраться, я привожу ниже расшифровку этапов пути двух лучей, где индекс ii относится к 1-у лучу, а jj ко 2-у.

ii = 10 от источника до левой грани призмы 3 (если А3=А3/2 то прямо до экрана без призмы и зеркала по ii = 18)

ii = 11 (если А3=А3/2 и + А4, то мимо призмы до дополнительного зеркала 4, а потом до зеркала 1 и до экрана)

ii = 14 от призмы до левого зеркала 1

ii = 18 от левого зеркала 1 до экрана

jj = 20 от источника до правой грани призмы 3

jj = 21 от правой грани призмы 3 до стеклянной крышки цилиндра с воздухом

jj = 22 от левого края стеклянной крышки цилиндра с воздухом до правого края крышки (здесь в расчете используется толщина сразу двух крышек)

jj = 23 от правого края (двойной) стеклянной крышки цилиндра с воздухом до конца цилиндра с воздухом

jj = 24 от правого края цилиндра до правого зеркала 2 (или от правой грани призмы 3 до правого зеркала 2)

jj = 28 от правого зеркала 2 до экрана

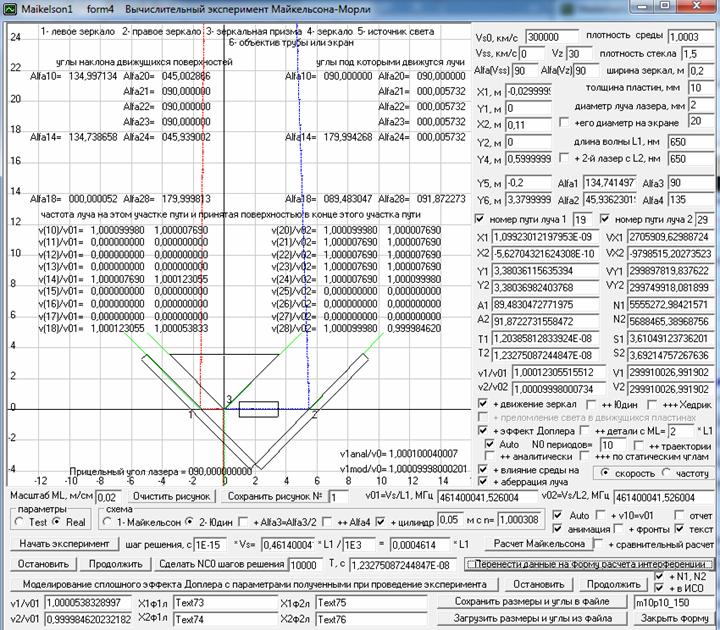
Рис. 35. Скриншот программы Maikelson1 после выполнения вычислительного эксперимента m3p11_338 при наличие цилиндра длиной 5 см с давлением воздуха в нем, дающем оптическую плотность 1,000308.

Как видим, на 10-м и 20-м участках пути, т.е. от лазера до боковых граней треугольной призмы, частота света уже не равна частоте лазера, т.к. он тоже вместе с установкой движется в АСО с заданной мною скоростью Vz= 30 км/с. При этом в нижнем правом углу рисунка я даю два значения этой частоты в долях исходной частоты лазера v1anal/v0, т.е. рассчитанной аналитически по формуле Лоренца (7-1) для эффекта Доплера, где скорость приемника Vp будет равна нулю, и смоделированной v1mod/v0, т.е. рассчитанной, как и для всех участков пути, при моделировании движения двух фронтов волн. И при этом у меня во всех дальнейших расчетах, если я моделирую эффект Доплера, т.е. когда отмечен чекбокс <+ эффект Доплера>, используется именно смоделированная частота света, хотя в этом простейшем случае можно было бы использовать и частоту полученную аналитически, а не численными методами при моделировании. Но в программе есть возможность при моделировании процессов движения лучей использовать и аналитический расчет эффекта Доплера, если отметить еще и чекбокс <++ аналитически>. А, если отметить еще и чекбокс <+++ по статическим углам>, то в формуле (7-2), которую я использую для аналитического расчета эффекта Доплера, будут использоваться проекции скорости луча света и отражающей поверхности на нормаль к этой поверхности, где нормаль будет браться от углов наклона поверхностей в статическом положении, а не от динамических углов наклона этих поверхностей, если этот чекбокс не отмечен.

v= v0*(1 - Vp / Vs) / (1 - Vi / Vs) (7-1)

v= v0*(1 + V21/V12) / (1 - V21/V12) (7-2)

При этом суть формул (7-1) и (7-2) остается одной и той же, т.к. в формуле (7-1), где используются скорость приемника сигналов Vp и скорость источника сигналов Vi, они тоже берутся в проекции, но на вектор скорости света Vs в направлении от движущегося источника, где расположен передатчик с частотой v0, на движущуюся поверхность приемника. Но у меня в формуле (7-2) v0 это уже частота самого света, падающего на движущуюся поверхность, а не частота передатчика, и у меня движущаяся в АСО поверхность является одновременно и приемником и источником. При этом проекция скорости света на нормаль V12 берется положительной в направлении к движущейся поверхности, а проекция скорости движущейся поверхности на нормаль V21 берется положительной в направлении навстречу лучу света. И при этом имейте ввиду, что отражение первого луча от полупрозрачного зеркала 3 в установке Майкельсона происходит не в воздухе, а в стекле и, следовательно, в формуле (7-2) должна фигурировать не скорость света в воздухе, как это будет при отражении от зеркал, а скорость света в стекле, которая примерно в 1,5 раза меньше, чем в воздухе.

А выбор таких знаков у скоростей V12 и V21 обусловлен тем, что эти скорости используются у меня и при определении времени, когда центры лучей коснутся движущихся поверхностей, и при определении времени, когда края фронтов волн или при определении эффективных углов наклона поверхностей или в случае с эффектом Доплера, коснутся этих поверхностей. А здесь я для определения этих моментов времени нахожу на каждом шаге решения расстояние между точкой или центра луча или края фронта и поверхностью, используя формулу для нахождения расстояния между заданными координатами точки и уравнением прямой, т.е. уравнением отражающем наклон движущейся поверхности. И, когда это расстояние получается меньше заданной мною точности решения этой задачи, я и фиксирую момент касания точкой этой поверхности. Но, т.к. при разном угле падения лучей света на движущуюся поверхность у нас за один шаг решения уравнений модели будет получатся разная точность определения времени касания лучом поверхности, я использую скорость точки и поверхности в проекции на нормаль к уравнению прямой, чтобы точность решения всегда была одинаковой. А эта точность решения уравнений у меня задается расстоянием, которое проходит свет за один шаг решения и на рис. 35 мы видим, что в этом вычислительном эксперименте это было 0,0004614 длины волны света.

Но в вычислительных экспериментах m3p11_338 я задал скорость перемещения установки равную скорости Земли относительно Солнца и поэтому эффект Доплера не очень заметен. А, чтобы вы увидели явное различие в частоте света двух лучей, движущихся на различных этапах пути от лазера до экрана, и явное влияние динамических углов наклона зеркал на углы отражения лучей, я сейчас выполню вычислительный эксперимент m3p3_80 с очень большой абсолютной скоростью установки 30000 км/с, т.е. равной 1/10 от скорости света. При этом я выполню два эксперимента - с углом скорости всей установки 0 градусов и 90 градусов. Как мы видим на нижнем рис. 36 у нас углы отражения лучей от граней движущейся горизонтально призмы получились такие же, как и в покоящейся установке, но это объясняется тем, что из за аберрации луча лазера углы падения лучей были не такие как в статике. А вот на верхнем рисунке у нас явно проявился эффект динамических углов наклона зеркал, но нам здесь более интересно как у нас повлиял эффект Доплера на частоту отраженных лучей. И, если на верхнем рисунке у нас частота света отраженных от призмы лучей хоть и изменилась, но для обоих лучей она на одинаковых участках пути получилась одинаковой, что объясняется тем, что обе грани призмы удалялись от падающих на них лучей, то на нижнем рисунке мы видим, что частота отраженных лучей v(14) и v(24) получилась очень даже разной.

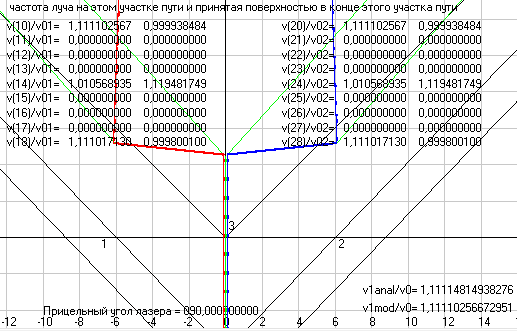
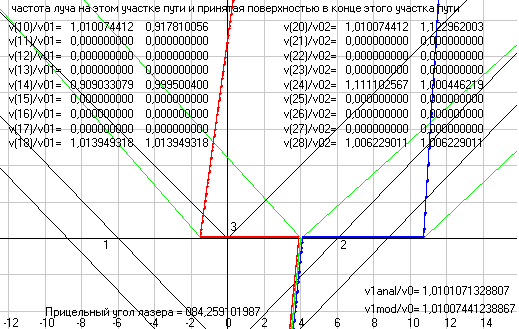
Рис. 36. Влияние абсолютной скорости установки на динамические углы наклона зеркал и на частоту отраженных от них лучей света при скорости установки равной 1/10 скорости света. Верхний рисунок при угле скорости установки 90 градусов и нижний 0 градусов. Скриншоты программы Maikelson1.

Таким образом, анализируя все вышеприведенные данные, я пришел к выводу, что не учитывать эффект Доплера в экспериментах на установках Майкельсона и моей нельзя, т.к. он обязательно должен был повлиять на конечный результат. Более того, во всех натурных экспериментах на установке Майкельсона, выполненных до меня, наблюдалось постоянное смещение полос даже в покоящейся установке, а это вполне можно объяснить не только нагревом лучами света поверхностей зеркал и полупрозрачной пластины, но и разностью частот двух лучей, падающих на экран. А у меня при быстром вращении моей установки и установки Майкельсона в разных направлениях тоже наблюдалось смещение полос то в одну, то в другую сторону, что тоже можно объяснить эффектом Доплера. Но все расчеты этого эффекта при моделировании функционирования установок (как моей, так и Майкельсона) дают такую большую разность частот двух лучей падающих на экран (даже при абсолютной скорости установки 30 км/с, как мы это видим на правом графике рис. 33), что становится ясно, что эти расчеты ошибочны. А я ведь предусмотрел в программе и моделирование эффекта Доплера и расчет его по аналитической зависимости (причем, как со статическими углами наклона поверхностей, так и с динамическими) и при этом никаких ошибок я в своих расчетах не нашел.

И вот на этом этапе своего исследования я надолго застрял, т.к. без разрешения этого противоречия дальнейшие исследования были бы бессмысленны. Да, можно было бы, как делали все до меня, проводя натурные эксперименты на установке Майкельсона, крутить туда сюда зеркала, менять длину плеч и т.д., надеясь на случайное появление какого то эффекта. Но даже в этом случае, не имея хорошей теории этого эксперимента, не возможно будет потом правильно интерпретировать этот эффект, т.е. сделать правильные выводы по полученным результатам. Поэтому я продолжал искать различные варианты разрешения этого противоречия и решил смоделировать эффект Доплера не рассматривая движение двух фронтов волн на каждом этапе движения лучей, а рассмотрев их движение одним проходом от лазера до экрана. И на рис. 37 вы видите результаты, которые получились при этом, если повторить эксперименты отраженные на рис. 36 для варианта движения установки вдоль оси Х.

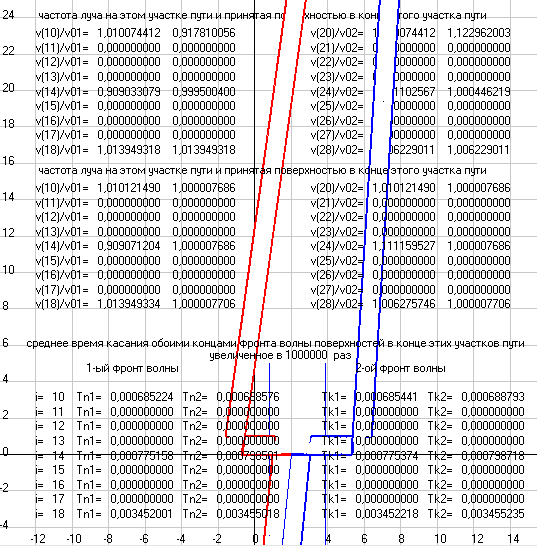
Рис. 37. Моделирование сплошного эффекта Доплера в эксперименте m3p3_80 при скорости установки равной 1/10 скорости света и при угле скорости 0 градусов с уточненным шагом решения в 100 раз меньше основного шага решения P00=1*10^-15 с и диаметром луча лазера 20 мм. Скриншот программы Maikelson1.

Здесь два общих фронта волны, вылетевшие из лазера согласно левого рис. 34, прошли сквозь фиктивный приемник и далее полетели к треугольной призме, где они каждый разделились на два более узких фронта волн и отразившись от левой и правой грани призмы, согласно правому рис. 34, полетели попарно к своим зеркалам. А на пути к зеркалам они тоже прошли сквозь фиктивные приемники и отразившись от зеркал полетели к экрану. Где и на этом этапе они прошли сквозь фиктивные приемники и потом были приняты экраном, т.е. уже реальным приемником движущимся вместе с установкой в АСО. Как видим, здесь даже при не очень маленьком уточненном шаге решении (P00/100) частота света в двух лучах, принятых поверхностью экрана, оказалась одинаковой v(18)=v(28)=1,000007706 (см. среднюю таблицу) и практически равной частоте лазера. А до этого при отдельном моделировании эффекта Доплера для каждого участка их путей, с заданием каждый раз двух фронтов волн летящих строго друг за другом, у нас была очень разная частота света этих лучей v(18)=1,013949318 и v(28)=1,006229011 (см. на этом же рисунке верхнюю таблицу). И при этом, как видно из средней таблицы, у нас получилась практически одинаковой и частота света принятая всеми поверхностями установки. А отсюда следует вывод, что полосы в натурных экспериментах и не должны были постоянно смещаться в одну сторону, как мы это видели на правом графике рис. 33, если у нас установка не вращается, а только движется под каким то углом. И, т.к. этого постоянного смещения в моих натурных экспериментах и не наблюдалось, то более правильным при моделировании эффекта Доплера является его расчет при сплошном движении двух фронтов от лазера до экрана. А разница здесь получается только в том, что при раздельном моделировании эффекта Доплера, я задавал движение двух фронтов летящих строго один за другим, а при сплошном моделировании у нас получается, что второй фронт всегда будет в АСО немного смещен в сторону (или влево или вправо) от первого фронта.

И оказывается вот такая мелкая деталь и дает принципиально другие результаты, но как задать это смещение при раздельном моделировании я пока так и не придумал. Поэтому я сейчас сначала провожу обычный вычислительный эксперимент, где или моделирую раздельный эффект Доплера или вообще его не учитываю, а потом, уже зная углы под которыми будут двигаться лучи при отражение от движущихся поверхностей, провожу вычислительный эксперимент со сплошным моделированием эффекта Доплера и уточняю количество колебаний в лучах света N10 и N20 на всем их пути от лазера до экрана а также частоту принятую поверхностью экрана v1/v0 и v2/v0. И уже с этими данными я перехожу на форму 3 программы Maikelson1, где произвожу расчет интерференционной картинки, которая должна получаться с такими параметрами двух лучей падающих на экран. А вот здесь у меня так и осталась не решенной до конца проблема выбора методики расчета начальных фаз двух лучей поэтому я пока экспериментирую со всеми пятью методиками, которые я приводил выше. Вот давайте сейчас и посмотрим, что у нас получится с использованием этих пяти методик для эксперимента с движением установки с абсолютной скоростью Vss=300 км/с под разными углами, если мы будем уточнять получающиеся данные моделированием еще и сплошного эффекта Доплера. Вычислительные эксперименты проведем на установке собранной по схеме m3p3_80 и зададим основной шаг решения уравнений P00=1*10^-15 с, который будем уменьшать в 1000 раз при приближение лучей к различным поверхностям. И ниже я привожу некоторые данные, которые получаются при двух углах направления движения установки Alfa(Vss)=0 и Alfa(Vss)=90 градусов.

Alfa(Vss)=0 v1/v0=0,99999988 N10=1308289,202 dN0=12,413 dN(t)=13,862 dN(x)=0,020

v2/v0=0,99999997 N20=1308301,615

Alfa(Vss)=90 v1/v0=0,99999990 N10=1310820,950 dN0=0,004 dN(t)=0,001 dN(x)=0,000

v2/v0=0,99999990 N20=1310820,953

Здесь мы видим, что при угле скорости 90 градусов частота света двух лучей, принятая экраном, совпала идеально, что, естественно, и должно было быть, т.к. два луча двигались по двум симметричным путям, но даже в этом случае мы видим, что количество колебаний света в двух лучах, сделанных на пути от лазера до экрана, все таки немного отличается на величину dN0=0,004 периода, что является погрешностью численного решения системы уравнений. А, если мы рассчитаем N10 и N20 по времени движения двух лучей (T1 и T2) и частоте лазера v0, то в этом случае у нас будет разность количества колебаний dN(t)=0,001 периода. А вот разность начальных фаз двух лучей вызванная разным местом падения их на экран dN(x) будет равна практически нулю, т.к. я специально подобрал углы наклона зеркал такие, чтобы эта погрешность была минимальной. Кстати, симметричность моей установки является и принципиальным отличием от установки Майкельсона, где нет никакой симметричности и поэтому нет никакой возможности зафиксировать полупериодический эффект, который все исследователи пытались обнаружить. Но вот при угле скорости 0 градусов мы видим, что у нас при заданном шаге решения погрешность определения частоты света падающего на экран будет уже в 7-ом знаке после запятой, что при такой погрешности на всех этапах движения двух лучей даст при общем количестве колебаний света 1310820 периодов максимальную погрешность в 0,131 периода.

Да, это значительная погрешность, но я не стал увеличивать точность решения, т.к. время выполнения одного вычислительного эксперимента и так было уже больше часа, а, если увеличить точность в 10-ть раз, т.е. уменьшить шаг решения еще в 10-ть раз, то время расчета тоже увеличится почти в 10-ть раз. К тому же результаты у меня получились такие, что на их фоне эта погрешность в 0,131 периода будет не значительной. Ведь, как мы видим при угле скорости 0 градусов у нас разность фаз двух лучей падающих на экран получается dN0=12,413 периода. А, если мы эту разность фаз будем рассчитывать по времени движения двух лучей до экрана, т.е. так, как рекомендуют делать в учебниках, то она получится еще больше dN(t)=13,862 периода. И, если к этим начальным разностям фаз двух лучей прибавить еще разность фаз dN(x), т.е. вызванную разными местами падения двух лучей на экран, то смещение полос получится еще чуть-чуть побольше. При этом, т.к. у меня разность фаз определяется как N2-N1, то положительная разность фаз означает, что полосы должны на такое количество сместиться влево, а у меня такое их направление имеет знак минус. Поэтому на графиках рис. 38 вы видите эти значения смещения полос в долях их ширины на -12 и -13 полос (это, соответственно, красная и розовая кривые). Здесь же на этом рисунке я привожу и графики смещения полос, которые получаются по 3-ей, 4-ой и 5-ой методикам расчета начальных фаз двух лучей (соответственно, черная, синяя и голубая кривые).

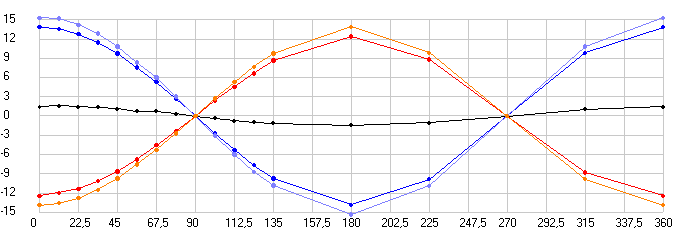
Рис. 38. Графики смещения полос при разном направлении движения Земли с абсолютной скоростью Vss= 300 км/с на установке собранной по схеме m3p3_80 и при моделирование сплошного эффекта Доплера с уточненным шагом решения в 1000 раз меньше основного шага решения P00=1*10^-15 с и диаметром луча лазера 20 мм. Здесь красная кривая и розовая получена при расчете начальных фаз по 1-ой и 2-ой методикам, а черная, синяя и розовая по 3-ей, 4-ой и 5-ой методикам. Графики построены с использованием программы Grafik4.

К сожалению проверить в натурном эксперименте, эти данные очень сложно, т.к. и при вращение моей установки, как это было видно в файле [31], наблюдаются медленные смещения полос в одну сторону, при вращение установки на подвесе против часовой стрелки и потом в другую сторону при вращение установки по часовой стрелке. А вот, чтобы выяснить наблюдается ли какая то связь между скоростью вращения установки и смещением полос, я повторил этот эксперимент с большей скоростью вращения установки, как это зафиксировано в файле [32]. В первом файле я предварительно закручивал нить подвеса примерно на пол оборота и поэтому после того, как я пережигаю другую нить, которая удерживает установку от раскрутки, она то раскручивается, то закручивается очень медленно. А во втором файле я предварительно закрутил нить подвеса более чем на два оборота и поэтому она раскручивается гораздо быстрее и при этом и полосы смещаются гораздо быстрее. В таблице ниже я привожу значения времени поворота установки в прямом направлении (против часовой стрелки) и в обратном, которые я определил визуально по этим двум файлам, а также количество оборотов, которое при этом сделала установка и количество полос, на которое они при этом сместились. С начала идет время, потом через дробь количество оборотов, потом количество полос и затем рассчитанные по этим данным средние скорости вращения установки (обороты/сек) и смещения полос (штук/сек). При этом в первых двух строках идут данные по 1-у прямому вращению (1пр) и 1-у обратному (1об), а потом по 2-у прямому вращению и обратному.

Таблица 12. Смещение полос при вращение установки Юдина собранной по схеме m81p81_856_1060, где размеры указаны в миллиметрах, при разном начальном угле закрутки нити подвеса.

________________1-ый_файл_____________________2-ой_файл

1пр_________53/0,90/6,40/0,0170/0,121________67/3,75/18,0/0,0560/0,269

1об_________53/0,75/6,10/0,0151/0,115________56/1,85/12,5/0,0330/0,223

2пр_________51/0,75/5,30/0,0147/0,104________54/1,50/9,80/0,0278/0,181

2об_________52/0,70/4,95/0,0135/0,095________53/1,20/8,60/0,0226/0,162

Если нанести эти данные на график, то они отлично ложатся на прямую, выходящую из начала координат, кроме 1-го прямого прохода во 2-м файле, где почему то получился очень большой период времени раскрутки, хотя, как видно по остальным данным, период собственных колебаний такого маятника примерно 52 секунды. С чем это связано я не знаю. Могу только предположить, что при такой большой скорости вращения установки было очень большое аэродинамическое сопротивление при ее вращении или в нити подвеса было большое сухое трение, т.к. она была не достаточно жесткая, но в любом случае я выкинул эту точку из аппроксимации. И в результате я получил вот такую зависимость скорости смещения полос от угловой скорости вращения моей установки Vb(полос/с)= 7,0 * Wsr , где Wsr это средняя скорость вращения установки в одном направлении (оборотов/с).

Таким образом при очень-очень медленном повороте установки мы могли бы практически обнулить полнопериодический эффект и наблюдать смещения полос, вызванные только от разного направления в пространстве скорости движения всей установки. Только для этого я должен поместить свою установку в ванну со ртутью, как делали почти все с установкой Майкельсона, т.к. вращение на подвесе не может обеспечить такой маленькой скорости поворота установки. Но, к сожалению, для меня такой вариант отпадает, т.к., во-первых, получается очень дорогостоящая установка, а, во-вторых, меня тут же арестуют, как только правоохранительные органы узнают, что я хочу приобрести такое количество очень ядовитого металла. К тому же скорость поворота установки при этом должна быть такой маленькой, что она должна быть сопоставима со скоростью вращения Земли вокруг своей оси, а при этом отпадает и необходимость в принудительном вращение установки, но время эксперимента становится таким большим, что малейшие колебания температуры приведут к гораздо большему смещению полос от этого, чем от поворота установки. Так что это направление исследований с медленным поворотом установки я считаю бесперспективным.

А пока и без этих экспериментов с очень медленным поворотом установки, надо сделать вывод о том, что или у меня в математической модели есть какие то ошибки или вся Солнечная система имеет абсолютную скорость гораздо меньше, чем 300 км/с. Ведь при проведение натурных экспериментов я при повороте своей установки не наблюдал таких больших смещений полос, полученных на математической модели и приведенных в табл. 12, даже с учетом их смещения от полнопериодического эффекта. Здесь, правда, надо заметить, что такой вывод справедлив, если эта скорость направлена в плоскости движения лучей в установке, а, если она направлена перпендикулярно этой плоскости, то она не будет оказывать практически никакого влияния на смещения полос и надо будет учитывать только скорость Земли относительно Солнца. Вот только Земля то у нас вращается и поэтому плоскость самой установки постоянно изменяет свой наклон к эклиптике и, следовательно, в разное время суток у нас в плоскости установки будут разные составляющие как от скорости всей Солнечной системы, так и от скорости Земли. И при этом они будут разные еще и в одно и тоже время в направлении юг-север и запад-восток. Но в любом случае, даже при использовании 3-ей методики, у нас получаются очень заметные смещения полос +/- 1,5 полосы.

Поэтому возможно, что и модель у меня правильная и скорость Солнечной системы близка к 300 км/с, а не правильные все пять методик расчета начальных фаз двух лучей, которые я использовал. А тут у меня, после изобретения 4-ой и 5-ой методик, просто иссякла фантазия. К тому же я отлично понимаю, что безупречной в теоретическом плане является только 3-я методика, но она отказывается работать при движение одного из лучей в более плотной оптической среде. А заставить ее работать и в этом случае получается только выдвинув почти сумасшедшую гипотезу о том, что в более плотных оптических средах уменьшается не скорость света, а его частота. Но для подтверждения этой гипотезы надо провести специальное исследование на очень дорогом оборудование, как, например, демонстрируемое в этом видеофайле [35], которое позволяет измерить скорость света в средах с различной оптической плотностью в одном направление. Так что прежде, чем продолжить свое исследование, мне есть над чем подумать в плане как работы над своей математической моделью и методикой расчета начальных и конечных фаз двух лучей, падающих на экран, так и работы над усовершенствованием конструкции своего интерферометра. И здесь я пока сосредоточу все свои усилия на выявлении смещения полос вследствие эффекта Доплера, который будет приводить к разной частоте света в двух лучах падающих на экран, т.к. при постоянном смещении полос из-за этого эффекта в покоящейся установке можно довольно точно определить их смещение, если для этого или не потребуются очень большие промежутки времени или эффект Доплера значительно превзойдет эффект от температурных деформаций.

P.S. Статья уже была закончена, когда я решил перепроверить все свое оборудование, т.к. полученная мною разница в наблюдаемой ширине полос и в рассчитанной по формулам (5-2), (5-4) и (5-5) или смоделированной с расчетом конечных фаз двух лучей в произвольных точках экрана по формулам (4-1), была очень заметной, как мы это видели и в табл. 3 и в других экспериментах, а поэтому не давала мне покоя. Проверка оборудования ничего не дала, т.к. и разрешение матриц вэбкамер получилось примерно такое же и коэффициент увеличения объектива кинопроектора получился примерно такой же. И тут я обратил внимание на то, что в формулах (4-1) у меня получаются конечные фазы двух лучей, т.е. не в точках их падения на экран, а в произвольных точках экрана, для разных моментов времени. Ведь по своей 3-ей методике я согласовал начальные фазы двух лучей, т.е. для одного и того же момента времени, только для точек, куда падают центры лучей, но потом я нахожу время распространения зайчиков напряженности от этих точек до произвольных точек на экране и рассчитываю конечные фазы двух лучей по формулам (4-1) или в будущем или в прошедшем времени. Но взаимодействовать между собою два луча и в произвольных точках экрана будут только тогда, когда их зайчики напряженности одновременно прибудут в эти произвольные точки.

Следовательно, надо уточнить мои формулы (4-1) с учетом еще и времени движения зайчиков напряженностей до этих произвольных точек с координатой Х так, чтобы зайчики напряженности прибывали в эти точки одновременно. Но тут я сразу уперся в то обстоятельство, что я не знаю точное значение длины волны своих лазерных модулей, чтобы знать результат, который я должен при этом получить. Хотел использовать для определения их длины волны угол преломления на треугольной призме лучей с разной длиной волны, но тут уперся в то обстоятельство, что я не знаю коэффициент преломления стекла, т.е. его оптическую плотность, из которого изготовлена моя призма. К тому же и тут надо было опять таки использовать одну из методик, которые я применял для расчета начальных фаз двух лучей, но теперь уже для расчета конечных фаз, т.е. в произвольных точках экрана. А, т.к. я пока не определился с тем, и какая методика является правильной и какова реальная длина волны, используемых мною лазерных модулей, то я решил пока повременить с этим расчетом. Тем более, что, вследствие очень больших скоростей зайчиков напряженностей, это уточнение формул (4-1) даст незначительные поправки и поэтому не повлияет принципиально на сделанные в статье выводы.

Перепроверить я решил и то в какую сторону смещаются полосы при увеличение давления в цилиндре, т.к. именно этот эксперимент заставил меня отказаться от теоретически безупречной 3-ей методики расчета начальных фаз двух лучей падающих одновременно на экран и изобретать 4-ю и 5-ю методики. При этом я категорически не хотел для увеличения ширины полос использовать в этом контрольном эксперименте оптику кинопроектора, которая переворачивала изображение на 180 градусов, т.к. мне хватало и переворотов самой вэбкамеры. А снимать установку с подвески и прикручивать удлинительный брус было просто лень. Поэтому я собрал свою установку по схеме "b", которая позволяла даже в этом случае получить составные полосы приличной ширины. Вот только, как видно из видеофайла [36], результат оказался очень неожиданным, т.к. полосы вопреки предыдущим натурным экспериментам в видеофайле [34] и вопреки теоретическим расчетам смещались совсем не в ту сторону что я ожидал увидеть при использование 4-ой и 5-ой методик, а смещались в ту сторону, которую давали 1-я и 2-я методики. Я даже повторил этот эксперимент без поворота в программе ContaCam изображения на 180 градусов, чтобы убедится, что эта функция правильно работает в этой программе. Но, как видно из результата в видеофайле [37], эта функция работает и, следовательно, в контрольном эксперименте направление смещения полос определено верно.

Тут я уже засомневался в том правильно ли я определил направление смещения полос в ранее проведенных экспериментах отраженных в видеофайле [34], т.к. там я не отобразил документально, т.е. не зафиксировал в самом видеофайле текущее положение переключателя в программе ContaCam, который позволяет при выводе изображения с вэбкамеры на экран ноутбука повернуть изображение на 180 градусов. Поэтому я решил срочно повторить два эксперимента из видеофайла [34] с фиксацией положения этого переключателя и с проверкой реальной ориентации положения полос на матрице вэбкамеры, как я это сделал в видеофайле [36], где я поднес линейку к матрице вэбкамеры сначала снизу, а потом слева и увидел тень от линейки на экране снизу и справа. Но, как мы видим в видеофайлах [38] и [39], где я повторил два эксперимента из ранее проводившихся, когда я собирал свою установку по схемам "a" и "c", и тогда и сейчас я правильно определил направление смещения полос, т.е. при увеличение давления на 110 мм.рт.ст и тогда и сейчас полосы смещались вправо на 3-и полосы. Но в контрольном эксперименте, когда я собрал свою установку по схеме "b", полосы так же смещались на 3-и полосы, но влево. А моделирование интерференционной картинки давало такое направление при использование 1-ой и 2-ой методик, хотя ранее я их забраковал, т.к. в ранее проводившихся экспериментах правильное направление смещения давали 4-я и 5-я методики.

В общем, я, как и планировал, на этом этапе прекращаю свое исследование, а в дальнейшем мне придется еще подумать над тем, как разрешить противоречие 3-ей методики при наличие на пути одного из лучей участка пути с более плотной оптической средой и при этом, чтобы она при разной схеме моей установки давала правильное смещение полос. Надеюсь, что и читатели, ознакомившись с этой статьей, выскажут какие то свои мысли по вопросу нахождения правильной методики определения начальных фаз двух лучей для одного и того же момента времени их падения на экран. А что касается 1-ой, 2-ой, 4-ой и 5-ой методик, то данные на рис. 38 заставляют сомневаться в правильности всех этих методик, т.к. они дают при проведение вычислительных экспериментов на математической модели моей установки просто огромные значения смещения полос, когда в установке отсутствует цилиндр, а установка движется с абсолютной скоростью 300 км/с.

Выводы

1.- Созданные мною математические модели интерферометров Майкельсона и моей конструкции описывают основные явления протекающие в этих установках и поэтому позволяют проводить на этих моделях вычислительных экспериментов даже в тех условиях, которые не возможно создать при проведении натурных экспериментов. При этом я согласен, что возможно какой то эффект я не учел в своих математических моделях или учел, но не совсем корректно, но основные эффекты я все же учел и учел их более-менее корректно.

2.- Время движения двух лучей от источника до приемника, которое было положено в основу теории эксперимента Майкельсона-Морли, не имеет к теории этого эксперимента никакого отношения, т.к. интерферировать между собою будут только два луча упавшие в одно и тоже место на экране одновременно.

3.- При интерференции мы можем наблюдать как обычные полосы, о которых пишут в учебниках, так и, как я их назвал, "составные" полосы, которые состоят из группы отдельных полос, но визуально воспринимаются как сплошные полосы.

4.- Дальнейшие исследования по определению абсолютной скорости Земли требуют не только создания экспериментальной установки, где можно четко контролировать задаваемые параметры и фиксировать наблюдаемый эффект, но и дальнейших теоретических исследований по теории интерференции.

5.- Конструкция интерферометра для определения абсолютной скорости Земли должна быть симметричной, чтобы наблюдался полупериодический эффект и этот эффект должен появляться из-за разности частот двух лучей падающих на экран.

Список литературы

1. Майкельсон А. Относительное движение Земли и светоносный эфир (1881). в сборнике статей "Эфирный ветер". Под ред. Ацюковского В.А. М.: Энергоатомиздат, 2011. 419 с.

2. Майкельсон А., Морли Э. Об относительном движении Земли и светоносного эфира (1887). в сборнике статей "Эфирный ветер". Под ред. Ацюковского В.А. М.: Энергоатомиздат, 2011. 419 с.

3. Миллер Д.К. Эксперимент по эфирному ветру и определение абсолютного движения Земли, (1933). в сборнике статей "Эфирный ветер". Под ред. Ацюковского В.А. М.: Энергоатомиздат, 2011. 419 с.

4. - Демьянов В.В. Реализация интерферометра типа Майкельсона на эффектах первого порядка отношения V/c. 14 с. http://www.nsma.ru/arch/first_order_ru.pdf

5 Франкфурт У.И., Френк А.М. Оптика движущихся тел. М.: Наука, 1972 http://ritz-btr.narod.ru/frankfurt/frankfurt.html

6. Хедрик Е.Р. Доклад на конференции по эксперименту Майкельсона-Морли в обсерватории Маунт Вилсон, г. Пасадена, Калифорния, 4 и 5 февраля 1927 г. http://ivanik3.narod.ru/MM/EDVAA/Confer.doc или в сборнике статей "Эфирный ветер". Под ред. Ацюковского В.А. М.: Энергоатомиздат, 2011. 419 с.

7. Глушко Вл. П., Глушко Вл. Вл., Глушко Вит. Вл. Замалчиваемые результаты опытов Майкельсона и Миллера. 24 с. http://redshift0.narod.ru/Rus/Stationary/References/Glushko_3.pdf

8. Акельев Н.М. Специальная теория относительности А. Эйнштейна – величайшая афера в истории физики и альтернативная ей концепция Лоренца-Фиджеральда-Планка. Волгоград, 2013, 166 с http://akelevnm.narod.ru/aboutsto.htm

9. Munera, H.A., et al: "Observation of a Non-conventional Influence of Earth's Motion on the Velocity of Photons, and Calculation of the Velocity of Our Galaxy" Conference in Beijing. 2009. http://ether-wind.narod.ru/Munera_2009/MuneraEtAlBejing2009.pdf

10. Bryant S. Revisiting the Michelson and Morley experiment to reveal en Earth orbital velosity of 30 kilometers per second. Steve.Bryant@RelativityChallenge.Com http://relativitychallenge.com/papers/Bryant.CICS.MMX.Analysis.06302006.pdf

11. Юдин С.Ю. Модели и имитаторы. труды 5-ой международной научно-технической конференции Компьютерное моделирование 2004. Часть 1. СПб.: Нестор, 2004, 356 с. http://modsys.narod.ru/Stat/Stat_Est/Konf_SPB/mod_imi.html

12. . Юдин С.Ю. Эффект Доплера. 6-я редакция, 146 с. http://modsys.narod.ru/Stat/Stat_Est/Dopler6doc.zip,

4-я редакция, 131 с. http://modsys.narod.ru/Stat/Stat_Est/Dopler4doc.zip

13. Детлаф А.А., Яворский Б.М. Курс физики. Том III. Волновые процессы. Оптика. Атомная и ядерная физика. Т. 3. М.: Высшая школа, 1979. - 511 с. http://eqworld.ipmnet.ru/ru/library/books/DetlafYavorskij_t3_1979ru.djvu

14. Ландсберг Г.С. Оптика. учеб. пособие для вузов. М.: ФИЗМАТЛИТ, 2003. - 848 с.

15. Матвеев А.Н. Оптика. учеб. пособие для физ. спец. вузов. М.: Высшая школа, 1985. - 351 с.

16. Иродов И.Е. Волновые процессы. Основные законы. Т. 4. М., 1999, 256 с.

17. Википедия https://ru.wikipedia.org/wiki/Интерференция_света

18. Тема "Теория интерференции" на форуме SciTecLibrary http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1611847794/#22

19. Сивухин Д.В. Общий курс физики, т.4, Оптика, 1980, 752 с.

20. Дрюков В.М. Белые пятна волновой теории света. http://drjukow.narod.ru/bel.light.1.htm

21. Замятин А.Г. Принцип близкодействия. Свердловск, 1988, 153 с. http://yadi.sk/d/mpuZzuId1xkL5

22. Файл записи эксперимента на покоящейся установке Юдина в течение 30 часов. http://modsys.narod.ru/Video/Pokoy30T_500X.mp4

23. Файл записи эксперимента на покоящейся установке Майкельсона в течение 2,5 часа. http://modsys.narod.ru/Video/Maikelson_Pokoy2_5.mp4

24. Файл записи эксперимента на покоящейся установке Майкельсона в течение 2-х часов. http://modsys.narod.ru/Video/Maikelson_Pokoy2.avi

25. Файл записи эксперимента с отклонением пятна лазера на экране при повороте установки. http://modsys.narod.ru/Video/Tochka.mp4

26. Файл записи эксперимента при медленном вращение установки Майкельсона. http://modsys.narod.ru/Video/Maikelson_Vrashenie1.avi

27. Файл записи эксперимента при быстром вращение установки Майкельсона. http://modsys.narod.ru/Video/Maikelson_Vrashenie2.avi

28. Файл записи эксперимента при покоящейся установке Майкельсона с наклоном зеркал. http://modsys.narod.ru/Video/Maikelson_Naklon.mp4

29. Файл записи эксперимента на покоящейся установке Юдина при максимальной ширине полос. http://modsys.narod.ru/Video/Garaj.mp4

30. Файл записи эксперимента на установке Юдина при изменение температуры окружающей среды. http://modsys.narod.ru/Video/Pokoy4T_200X.mp4

31. Файл записи эксперимента при медленном вращение установки Юдина. http://modsys.narod.ru/Video/Vrashenie1.avi

32. Файл записи эксперимента при быстром вращение установки Юдина. http://modsys.narod.ru/Video/Vrashenie2.avi

33. Файл записи 2-х экспериментов на покоящейся установке Юдина при изменение давления в цилиндре длинной 10 см. http://modsys.narod.ru/Video/Cilindr_2exp.mp4

34. Файл записи 4-х экспериментов на покоящейся установке Юдина, собранной по схемам a и c, при изменение давления в цилиндре длинной 5 см. http://modsys.narod.ru/Video/Cilindr_4exp.mp4

35. Видео с Ютуба о работе оборудования позволяющего снимать 10 триллионов кадров в секунду. Filming the Speed of Light at 10 Trillion FPS

36. Файл записи контрольного эксперимента на покоящейся установке Юдина, собранной по схеме b, при изменение давления в цилиндре длинной 5 см. http://modsys.narod.ru/Video/Cilindr_control_1.mp4

37. Файл записи контрольного эксперимента на покоящейся установке Юдина, собранной по схеме b, при изменение давления в цилиндре длинной 5 см с поворотом изображения на 180 градусов. http://modsys.narod.ru/Video/Cilindr_control_2.avi

38. Файл записи повтора эксперимента на покоящейся установке Юдина, собранной по схеме c, при изменение давления в цилиндре длинной 5 см. http://modsys.narod.ru/Video/Cilindr_povtor_1.mp4

39. Файл записи повтора эксперимента на покоящейся установке Юдина, собранной по схеме a, при изменение давления в цилиндре длинной 5 см. http://modsys.narod.ru/Video/Cilindr_povtor_2.mp4

P.S. Все мои работы (в последних редакциях) можно найти на моем сайте http://modsys.narod.ru в разделе "Научные работы", а всю другую литературу, использованную мною при написание статей, в разделе "Моя библиотека". Кроме этого можно скачать и редакцию этой статьи в формате .doc 1-я редакция http://modsys.narod.ru/Stat/Stat_Est/Maikelson1doc.zip

А, если какие то видеофайлы к этой статье не открываются по приведенным выше ссылкам в окне вашего браузера, то просмотреть их можно вашим видеоплеером, скачав архив со всеми видеофайлами к этой статье по этой ссылке с моего яндекс диска https://disk.yandex.ru/d/93FPUAmujOxosw

Послесловие

Да, мне пока не удалось определить абсолютную скорость Земли ни по данным наблюдений за планетами Солнечной системы, ни по данным наблюдений за двойным пульсаром В1913+16 (где я пытался определить и скорость гравитации), ни с использованием интерферометра своей конструкции, но последний вариант я считаю самым перспективным. Ведь подходящая статистика по наблюдениям за планетами, которая позволит достоверно выявить смещения их параметров орбит, появится не ранее чем через десяток тысяч лет, а данных наблюдений за двойным пульсаром В1913+16 в режиме поиска, а не в режиме суммирования, которые можно получить всего за один день наблюдений за ним, как я выяснил вообще не существует (их сейчас ни у кого нет), хотя именно за эти данные, которые доказывают справедливость ОТО, открывателям этого пульсара дали Нобелевскую премию. А, т.к. получать устойчивый сигнал от этого пульсара можно было пожалуй только на одном радиотелескопе в Аресибо, который в прошлом году самоуничтожился, то теперь такие данные в обозримом будущем мы и не получим. Так что для определения абсолютной скорости Земли мне остается только использовать интерферометр моей конструкции. Вот только я пока не определился со схемой своего интерферометра.

Первоначально я думал модулировать сигналы от двух импульсных лазеров более низкой частотой от двух генераторов, где когерентность будет обеспечиваться стабильностью частоты генераторов, и в программе Maikelson1 у меня сейчас уже смоделирован такой вариант работы моего интерферометра. Но тут есть проблемы с генераторами, т.к. их частота должна измеряться в гигагерцах, а как я узнал из литературы, тут имеются проблемы в электрической части таких генераторов. К тому же пока не ясно должна ли быть и частота самих лазеров в этом случае когерентной. Поэтому сейчас я больше склоняюсь к схеме, где используется один лазер с разделением луча на два, а затем частота одного из лучей будет изменяться механически за счет вращения с разной скоростью барабана на котором будут установлены несколько зеркал. Хотя и тут я вижу проблему в том, что для устойчивого наблюдения полос, частота вращения барабана должна быть такой, чтобы луч отражался от зеркал не менее 20 раз в секунду. И даже, если радиус такого барабана будет 5 см и на нем будет четыре зеркала, то получается скорость движения зеркал около 1,5 м/с, а при такой скорости смещение полос будет очень быстрым. Ведь в проведенных мною натурных экспериментах полосы двигались очень быстро даже при скорости зеркал менее 0,5 м/с. Поэтому я пока еще подумаю над схемой моей установки для дальнейших экспериментов, а сейчас займусь повторением эксперимента Физо, где постараюсь доказать, что свет не увлекается потоками воды, а смещения полос, которые зафиксировал при этом Физо, были обусловлены увеличением давления воды в трубах при более высокой скорости ее прокачки.