МЕХАНИКА ДЛЯ КВАНТОВОЙ МЕХАНИКИ

                           Часть 4. Опять о принципе наименьшего действия

Юдин С. Ю.                                                                              modsys@narod.ru   ( modsys@yandex.ru )

                                                (первая редакция 03.09.2012)

 

 

Данная статья является продолжением моего исследования принципа наименьшего действия (ПНД), которое я начал в своей статье «О принципах кратчайшего времени и наименьшего действия» [21] и где я не только рассмотрел историю возникновения этого принципа, но и проверил его на наличие глобального минимума действия в различных формулировках и при движение в различных полях. В результате этого исследования я доказал на конкретных примерах, что ПНД соблюдается только локально и по этому не может претендовать на роль главного закона природы и посчитал, что на этом свое исследование можно закончить. Но после публикации статьи мои аппоненты, стали утверждать, что ПНД все равно самый главный закон природы, т.к. для того, чтобы он соблюдался, не надо никакого минимума действия, а достаточно, чтобы была равна нулю первая вариация, т.е. соблюдалось условие стационарности. На мои возражения о том, что в учебниках по теоретической физике Ландау и у Фейнмана этот принцип сформулирован, как требующий именно минимума действия на истинном пути, мне отвечали, что все равно Ландау и Фейнман имели ввиду только стационарность действия, т.к. для вывода из ПНД уравнений динамики требуется только стационарность. Это заставило меня более подробно ознакомится с текстом Механики у Ландау и интегралов у Фейнмана и продолжить исследование ПНД в том числе и на предмет его использования как принципа стационарного действия. Результатом этого исследования и является эта статья, где особое место отведено разбору Механики у Ландау и интегралам по путям Фейнмана.

 

 

И так, в 1744 году Мопертюи выдвинул принцип наименьшего действия исходя из метафизических представлений о Природе, где все должно происходить из каких то разумных соображений как будто бы Природа в своих действиях преследует какие то цели, которые сама перед собою и ставит, т.е. имеется в виду наличие Бога, который осуществляет в Природе только разумные процессы. Кстати, и уже в ХХ веке Планк [9] пишет о сущности этого принципа так «В связи с этим надо вспомнить о Теодице Лейбница, в которой выдвинут тезис о том, что истинным миром среди всех миров, которые могли бы быть сотворены, является тот мир, который наряду с неизбежным злом содержит в себе максимум добра. Этот тезис является не чем иным, как вариационным принципом, выраженным в такой же форме, как возникший позднее принцип наименьшего действия. Неизбежное сцепление добра и зла играет при этом роль предписанных условий, и ясно, что фактически из этого тезиса могли бы быть выведены все особенности действительного мира, если бы удалось математически точно сформулировать, с одной стороны, меру для количества добра, с другой стороны – предписанные условия». Кстати о Теодице Лейбница Планк вспомнил не зря, т.к. многие приписывали открытие этого принципа именно Лейбницу и страсти тогда разгорались не шуточные. Даже Вольтер посвятил одно из своих произведений этому принципу. А самому Мопертюи пришлось подключать даже царствующих особ, чтобы добиться своего приоритета в открытие этого принципа. Но и в начале 21 века есть люди, которые с использованием этого принципа оптимизируют водопровод в Воронеже и работу чиновников в Киеве (читал авторефераты диссертаций), т.е. продолжается обожествление этого принципа.

 

 

Сам Мопертюи, занимаясь статикой, привел свой принцип примерно в таких расплывчатых формулировках «количество действия, которое допускает произведенное изменение, является наименьшим возможным» и «природа во всех своих проявлениях пользуется наименьшей затратой действия». А самую первую математическую формулировку этого принципа дал его друг Эйлер, который со слов Лагранжа сформулировал его так «при траекториях, описанных под действием центральных сил, интеграл скорости, умноженной на элемент кривой, всегда является минимумом или максимумом». Лагранж, как вариант, рассмотрел замену в этом интеграле элемента пути ds на произведение V*dt и под интегралом получилось выражение m*V^2 * dt и, естественно, теперь интегрирование надо вести не по пути, а по времени от t1 до t2. Позже Гамильтон предложил другую формулировку этого принципа, где интеграл по времени берется от лагранжиана, т.е. предложил уже совсем другой принцип, который и предложил называть принципом переменного действия, но название для него оставили прежним – ПНД. По этому, сейчас, когда говорят об этом принципе, то указывают в какой формулировке его имеют ввиду и для краткости я буду обозначать разные формулировки как ПНД1 и ПНД2. У принципа в формулировке Эйлера-Лагранжа (ПНД1) действие вычисляется как интеграл по времени от кинетической энергии (Т), а в формулировке Гамильтона-Остроградского (ПНД2) действие вычисляется как интеграл по времени от лагранжиана, т.е. от разности кинетической и потенциальной энергии (T-U). Большой вклад в оба этих принципа внес немецкий математик Якоби, по этому, часто в названиях этого принципа фигурирует и его фамилия.

 

 

Надо сказать, что в то время, когда создавался ПНД, ученые старались найти какую то универсальную меру механического движения (закон сохранения энергии не был открыт и даже не было понятия кинетической энергии, не говоря уже о потенциальной). О том, какие тогда разгорелись споры о мере механической формы движения материи я подробно рассмотрел в своей статье [22]. По этому, с самого начала ПНД с его мерой движения «действие» создавался его основателями (Эйлер и Лагранж), чтобы доказать, что он является общим принципом Природы, в которой все процессы происходят разумно, т.е. с минимумом такой величины как действие и звучал так, что все движения в Природе из множества возможных траекторий происходят по истинным траекториям, где действие минимально. Смысла получившегося ПНД никто не понимал (не понимает и сейчас), но всем нужен был какой то общий принцип механики и по этому ПНД и стали таковым считать, а когда появился закон сохранения энергии, то было уже поздно – джина выпустили из бутылки и загнать его туда обратно стало очень трудно, т.к. за это время в механике столько нагородили, что без ПНД ее уже и не представляли.

 

 

Однако, как было показано в работе [34] все не так безнадежно и истинный смысл ПНД2, который он рассматривает повторяя выкладки Фейнмана, состоит только в соблюдении 2-го закона Ньютона

«Несомненно, что основной из этих принципов – принцип наименьшего действия “подгонялся” под второй закон Ньютона и обосновывался, исходя из этого, как некоторая вариация, которая почему-то всегда равна нулю, а не самом деле находилась такая функция, минимум которой определялся вторым законом Ньютона. Однако, как нами было показано, эта функция в результате математических операций преобразуется в другую функцию, которая не имеет ни максимума, ни минимума, поскольку является постоянной величиной и представляет собой закон сохранения энергии.»

Кстати, в этой работе говорится и о том, что

«В связи со всем изложенным можно утверждать, что принцип наименьшего действия Гамильтона является чисто математическим приемом по исследованию некоторой специально подобранной функции (в данном случае разности T-U).»

В общем очень интересный и замечательный параграф в книге (чего не могу сказать о всей книге) и я всем рекомендую с ним ознакомится, т.к. формат моей статьи не позволяет привести всех математических выкладок из этого параграфа.

 

 

А после изобретения ПНД, когда вариационное исчисление, опираясь на принцип минимума времени у Ферма и Бернулли и на ПНД, окончательно перебралось из геометрии в механику и стало оформляться в отдельную дисциплину в механике (основы аналитической механики Лагранжа), ПНД стали иногда называть принципом экстремального действия (ПЭД), т.к. уже и Эйлер и Лагранж заметили, что с математической точки зрения более корректно говорить о ПЭД. Но физический смысл в этот принцип все равно продолжали вкладывать как в ПНД, т.к. таких процессов, где бы действие было максимально на истинном пути я, например, не видел и по этому, когда я буду говорить о ПНД, то буду иметь ввиду и ПЭД.

 

 

Со временем многие ученые поняли, что ПНД в глобальном смысле в Природе не соблюдается и тогда стали говорить о нем как о принципе стационарного действия (ПСД), а пожалуй первым, кто употребил этот термин был Гамильтон. Таким образом, теперь даже ни о каком экстремуме не может быть и речи, т.е. на действительной траектории выполняется условие только равенства нулю первой вариации действия. Но равенство первой вариации нулю есть необходимое, но не достаточное условие экстремума [33]. Таким образом, если действие минимально или максимально на некотором пути, то вариация действия ноль, но если вариация ноль, то действие не обязательно максимально (минимально) даже локально, а для ПНД экстремум к тому же должен быть глобальный. Т.е. ни о каких конкретных значениях действия в ПСД не может быть и речи, т.е. никаких ни минимумов ни экстремумов. Однако, как писал Остроградский [13] «На самом деле вариация интеграла может обращаться в ноль и в том случае, когда интеграл не допускает ни наибольшего, ни наименьшего значения, но геометры обычно говорят и в этом случае о минимуме и максимуме, без сомнения, для простоты изложения, и мы будем в этом следовать их примеру». А вслед за геометрами, т.е. математиками, и физики почти всегда стали представлять этот принцип как ПЭД, но чаще всего формулировали его именно как ПНД. И я, например, видел формулировки ПНД, именно как ПСД, т.е. чтобы было написано, что «на действительном пути из точки 1 в точку 2 действие имеет стационарное значение» только в строгих академических изданиях по аналитической механике, а физики или математико-физики так и продолжают писать о минимуме или максимуме.

 

 

Например, вот формулировка Луи де Бройля [14], который называет этот принцип уже ПСД, но из изложения понятно, что говорит он о ПЭД, т.е. о том же ПНД, но в более широкой формулировке. «Уравнения динамики материальной точки в поле сил, обладающих потенциалом, можно получить, исходя из принципа, который в общем виде носит название принципа Гамильтона, или принципа стационарного действия. Согласно этому принципу, из всех движений материальной точки, которые она может совершить между теми же начальной и конечной точками за тот же самый промежуток времени t₂...t₁ в действительности осуществляется то движение, для которого интеграл по времени от t₁ до t₂ от разности кинетической и потенциальной энергий этой материальной точки принимает экстремальное, т.е. минимальное или максимальное значение. Особенно простую форму принимает принцип стационарного действия в частном, но важном случае статических силовых полей. В этом случае он совпадает с принципом наименьшего действия Мопертюи, согласно которому для действительного пути материальной точки в консервативном (т.е. не зависящем явно от времени) силовом поле интеграл от импульса частицы, взятый по отрезку траектории между какими-либо двумя ее точками A и B, минимален по сравнению с такими же интегралами, взятыми по отрезкам других кривых, проведенных через точки A и B».

 

 

И в учебнике по Механике Ландау и Лифшица [3] мы видим тоже самое - «Наиболее общая формулировка закона движения механических систем дается так называемым принципом наименьшего действия (или принципом Гамильтона).....Пусть в моменты времени t=t1 и t=t2 система занимала определенные положения, характеризуемые двумя наборами значений координат q(1) и q(2). Тогда между этими положениями система движется таким образом, чтобы интеграл (2.1) имел наименьшее возможное значение. Функция L называется функцией Лагранжа данной системы, а интеграл (2.1) действием».

 И у Фейнмана [26] формулировка ПНД в классической механике та же самая

«Одним из наиболее изящных способов выразить условия, выделяющие из всех возможных траекторий определенную траекторию x̃(t), является принцип наименьшего действия. Допустим, что существует некоторая величина S, которую можно вычислить для каждой траектории. Классическая траектория x̃ – это та, для которой S принимает минимальное значение. Фактически используют только условие экстремальности действия ; иными словами, значение S в первом приближении не изменится, если незначительно отступить от траектории x̃(t).»

 

 

Кроме того, идет ли речь о ПНД или о ПЭД, авторы приведенных выше формулировок, говоря о том, что действие при этом будет экстремально или минимально забывают еще уточнить, что, даже в тех случаях, когда мы имеем именно минимум или максимум, этот принцип не является глобальным, т.е. справедлив только для некоторой части пути и по этому является локальным. А чтобы применить его на этом локальном участке пути, надо знать границы его применимости, т.е. найти кинетические фокусы, т.к. за пределами этих границ ПНД не соблюдается. Почти все авторы учебников по аналитической механике, например, [5, 6] рассматривают вопрос о том будет ли действие на этом пути минимальным с привлечением кинетических фокусов. Вот только поиск этих кинетических фокусов оказался не таким простым делом и я нашел более менее полное описание правил, по которым их определять, только у Лурье [7]. Хотя уже у Лагранжа было немного по этому вопросу, а Якоби почти сформулировал общие правила их нахождения. При этом не надо забывать, что применять ПНД (даже локально) можно только при отсутствие диссипации энергии и желательно при отсутствии неголономных связей. Но даже соблюдение всех этих условий, когда ПНД действительно соблюдается, не позволяет нам решить ни одной конкретной задачи с использованием ПНД. Можно только из него получить классические дифференциальные уравнения, описывающие движение тела. Впрочем, точно также и из дифференциальных уравнений можно получить ПНД. Так почему же столько шума вокруг этого принципа.

 

 

Дело в том, что на ПНД возлагали большие надежды как на философский камень науки, который позволит получить с его применением все законы Природы, т.е. он создавался как закон для всех остальных законов Природы, по тому, что считалось, что по этому закону Бог управляет миром. Эта теологическая направленность ПНД нравилась не всем ученым и они постоянно высказывали недоумение по поводу применения этого принципа. Например, Герц писал  [37]

 «…немыслимо, чтобы принцип Гамильтона или другой принцип аналогичного характера представлял собой фактически основной закон природы;…принцип Гамильтона, если его детально проанализировать, представляет собой чрезвычайно сложное высказывание. Он не только ставит происходящее в настоящий момент движение в зависимость от последствий, которые могут выявиться в будущем, предполагая существование у неживой природы намерений, но что еще хуже, он предполагает существование у природы бессмысленных намерений. Ибо интеграл, минимум которого требует принцип Гамильтона, не имеет простого физического значения; кроме того, представляется непонятной целью природы приведение математического выражения к минимуму или его вариации к нулю».

 

 

 А Зоммерфельд наоборот, хотя вроде бы и предполагает некую теологическую основу этого принципа, но все равно протаскивает его в науку, т.к. считает, что его телеологичность нам только кажется [38]

 “Принцип Гамильтона, так же как и остальные принципы наименьшего действия, кажущимся образом противоречат нашему представлению о причинности, поскольку, согласно этому принципу, протекание процесса во времени определяется не состоянием системы в настоящий момент, а выводится с учетом в равной мере прошедшего и будущего системы. Интегральные принципы являются, казалось бы, не каузальными, а телеологическими”. И далее разъясняет нам, что “телеологический” это всего-навсего значит “целесообразный” или просто “целенаправленный”.

 

 

Но наиболее здравомыслящие ученые всегда относились к этому принципу как к неполноценному, по тому, что никто не понимал его физического смысла и, следовательно, плохо представлял когда, где и зачем его можно использовать. Например, когда Эйлер увидел, что на другой стороне шара, т.е. как сейчас говорят за кинетическим фокусом, ПНД не соблюдается, он прекратил им заниматься, а позже Пуассон вообще назвал его «лишь бесполезным правилом». А еще один из создателей этого принципа, а конкретно М.В.Остроградский в своей статье [13] об этом принципе сказал следующее

 «Формула (21) содержит как частный случай динамический принцип наименьшего действия, но, с нашей точки зрения, его нельзя рассматривать не только как принцип, но даже как простую теорему. Он кажется нам только простым следствием, очевидным результатом применения метода вариаций к теории maxima и minima».

Само собой возникает вопрос – а зачем он вообще этот ПНД нужен, если с ним столько непонятного и туманного. Аналогичным вопросом о назначении ПНД задается и автор лекции [29], который, кстати, очень нахваливает этот принцип

«В общем-то на этом следовало бы и закончить эту лекцию, но один вопрос, наверное, многим не дает покоя. Для чего все это делалось? Только ли для того, чтобы показать, что ньютоновская механика может быть сформулирована на основе совсем другого математического аппарата — вариационного исчисления? Но ведь все равно потом приходится решать все то же дифференциальное уравнение, выражающее собой II закона Ньютона, для определения траектории частицы. Тогда зачем все так усложнять? Имеет ли действие S, введенное нами выше, какой-то самостоятельный физический смысл?».

И с радостью отвечает – да имеет, но не в классической механике, а в квантовой.

 

 

Что касается квантовой механике, то я еще вернусь к этому вопросу, а сейчас продолжим рассмотрение ПНД как общего принципа Природы, по тому, что многие и сейчас пытаются придать этому принципу роль философского камня в науке и получить с его использованием все остальные законы Природы, а заодно и протаскивают Бога в науку, доказывая, что все процессы в Природе протекают разумно. Например, для нас будет особенно интересно то, что Ландау почти всю физику выводит из ПНД, а механику уж точно всю, получая из него уравнения Лагранжа. А связан наш интерес к этому учебнику тем, что сейчас его Курс теоретической физики является официальным учебником России. Хотя, например, Уиттекер в своей аналитической механике [6] наоборот из уравнений Лагранжа выводит ПНД и то только в 9-ой главе. Но здесь сторонники выводить что то из ПНД забывают об одной его особенности, а именно о том, что из ПНД можно получить только заранее известные и нужные именно тебе уравнения, о чем писал уже Эйлер, когда только формулировал этот принцип, т.к. при рассмотрение различных проблем в механике он убедился, что любая из них может быть решена без ПНД, а применение для этого ПНД требует предварительного знания их решений.

 

 

И здесь очень поучительна история борьбы в физике в конце 19 века с энергетическим течением в ней, когда и энергетики, и их противники использовали ПНД для обоснования своих позиций. По этому поводу Полак в своей редакционной статье к сборнику статей по ПНД [10] пишет

«Тот факт, что и энергетики, и их противники пользовались принципом Гамильтона, показывает, что один и тот же математический аппарат может служить для оформления различных физических картин. Физическая картина мира может строиться при помощи принципа Гамильтона, но не может быть из него выводима (если не знать заранее, что требуется получить)».

Интересен также и тот факт, что типичным афоризмом Ландау было выражение «Как Вы можете решать задачу, ответа на которую Вы не знаете заранее». По этому, конечно же, прекрасно зная, какие уравнения динамики надо получить, Ландау их легко и получает из этого принципа.

 

 

Впрочем, здесь надо еще и сделать некоторое уточнение о том, что не все уравнения можно получить из этого принципа. Так в Википедии говорится о том, что

«Необходимо заметить, что если из условий задачи принципиально можно найти закон движения, то это автоматически не означает, что можно построить функционал, принимающий стационарное значение при истинном движении. Примером может служить совместное движение электрических зарядов и монополей — магнитных зарядов — в электромагнитном поле. Их уравнения движения невозможно вывести из принципа стационарности действия. Аналогично некоторые гамильтоновы системы имеют уравнения движения, не выводимые из этого принципа.»

К этому, конечно же, надо добавить и то, что из ПНД нельзя получить уравнения движения если в системе имеется трение, т.к., во-первых, в этом случае ПНД просто не применим, а, во-вторых, в ПНД2 в лагранжиане, а в ПНД1 в формуле кинетической энергии для энергии рассеянной на трение просто нет места.

 

 

Так зачем же Ландау потребовалось обожествлять этот принцип в своем курсе теоретической физики. Ведь как писал Гамильтон [15]

«Но когда этот закон наименьшего, или, как его лучше было бы назвать, стационарного действия, применяется к определению фактического движения системы, он служит только для того, чтобы по правилам вариационного исчисления получить дифференциальные уравнения движения второго порядка, которые всегда можно получить другим путем. Поэтому Лагранж, Лаплас и Пуассон, по-видимому, не без оснований пренебрежительно отзывались о полезности этого принципа при тогдашнем состоянии динамики.»

И даже уже в ХХ веке Планк писал, что ПНД не оказал никакого влияния на науку, а у Ландау (кстати, еще до получения Фейнманом его интегралов по путям в 1942 году) в первом издание Механики этот принцип опять возрождается  как господствующий над всеми законами Природы. И из этого принципа у него более сложным методом получаются уравнения движения, которые в учебниках других авторов получаются более простым и понятным способом из основных аксиом механики. Ответить на вопрос «зачем делать именно так» не просто, но я попробую объяснить почему «нормальные герои всегда идут в обход».

 

 

Для этого нам надо немного погрузиться в ту атмосферу, когда создавался его курс теоретической физики (смотрите статью Карла Холла [30]). Ведь как сказал Сталин «написание учебников – непростое дело». К тому же искались и новые методы обучения студентов, например, попытка ввести в 1931 году «бригадный» метод образования. По этому и новые советские учебники должны были отличаться от старых буржуазных учебников и быть монументальными изданиями, отражающими какую то великую идею. И вот тут, как я думаю Ландау и пришла мысль объединить все разделы физики одной идеей, а именно принципом наименьшего действия, тем более, что она прекрасно подходила для теории поля (закончена была в 1939 году) и в частности для ОТО Эйнштейна, т.к. только ПНД с его действием удовлетворял требованиям лоренц-инвариантности. Здесь, наверное, уместно напомнить и то, что в 1938 году вышел Краткий курс Истории Всесоюзной Коммунистической Партии (большевиков), который весь был пронизан великой идеей построения коммунистического общества и изложен он был в манере не допускающих никаких сомнений или предположений. Так вот, и Курс Ландау написан им так, что тоже не допускает никаких сомнений в написанном в нем, т.к. все написанное вытекает из великой идеи ПНД, а посему должно быть единственно верным учением.

 

 

Вот только не все ученые должным образом оценили его революционные порывы объявить советскую науку о Природе единственно верной и, например, В.А.Фок в своей рецензии на первое издание Механики (в редакции Ландау и Пятигорского 1940 года) [16] написал, что

 «Переходя к оценке книги в целом, мы должны признать, что она авторам не удалась. ... Мы вправе требовать от них гораздо большего. А в более тонких и трудных вопросах механики – вариационный принцип, классификация типов движений механических систем – авторы оказываются решительно не на высоте: мы находим в соответствующих главах ошибки и путаницу.»

Я не буду здесь писать обо всех методологических и математических ошибках, которые обнаружил Фок и кому это интересно отсылаю к тексту рецензии, которая опубликована в УФН, 1946, т.28, вып.2-3. Скажу только, что ПНД в формулировке Ландау сильно досталось.

 

 

После этого, как мы знаем, следующее издание своей Механики 1958 года он писал уже с другим своим учеником Лифшицем, но практически расстался с Пятигорским Ландау не из-за разгромной рецензии на учебник, а гораздо раньше (в 1938 году), т.к. считал, что он причастен к его аресту в 1938 году. Позже он узнал, что это не так и снял с Пятигорского в 1956 году запрет на защиту им диссертации. Кстати он все тома своего курса (даже после смерти) писал с кем ни будь, т.к. сам ничего не писал, а только правил уже написанный текст. Так вот именно в этом издание 1958 года, которое отличалось от издания 1940 года процентов на 30%, и появилось множество ссылок к тексту 1940 года касающихся ПНД. После этого, по словам А.А. Рухадзе, "Механика" стала "самым отточенным" произведением Курса. Сейчас мы убедимся, что это не так. Сравнивать я буду издание 1940 года [1] и издание 1958 года [2], но при этом буду также использовать и издание 2004 года [3]. А для начала я воспроизведу замечания сделанные в рецензии Фоком по ПНД.

 

 

«В основу построения механики полагается принцип наименьшего действия (начало Гамильтона). Авторы исходят здесь из ошибочного представления, будто ”при заданных внешних условиях движение вполне определяется координатами начала и конца движения” (стр. 152). Что это представление не верно, особенно ясно видно на примере свободного движения материальной точки на поверхности шара. Если взять в качестве начальной и конечной точек два полюса, меридиан, по которому она движется, остается неопределенным до тех пор, пока не будет указано направление ее начальной скорости.

 

На самом деле, когда даны уравнения Лагранжа, движение определяется начальными координатами и начальными скоростями. А поскольку задание этих последних не эквивалентно заданию конечных координат, нельзя говорить и об эквивалентности между началом Гамильтона, с одной стороны, и уравнениями Лагранжа с начальными условиями, с другой стороны.

 

По этой причине полагать в основу механики принцип наименьшего действия едва ли правильно, даже и независимо от того, что этот принцип применим не ко всем системам. Мы уже не говорим о том, что принцип наименьшего действия труднее уравнений движения и что, по нашему мнению, нужно начинать с более легкого: в вопросах методики возможны разные мнения.

 

Говоря о принципе наименьшего действия, мы имели в виду известное экстремальное свойство интеграла действия: исчезновение его первой вариации. Авторы же понимают это наименование буквально: они считают, что всегда интеграл действия ”для действительного движения имеет минимальное значение” (стр. 13). Что это не верно показывает тот же пример движения точки на шаре. Если начальное и конечное положения не являются полюсами, то возможно “прямое” движение и “кругосветное”. Для прямого движения интеграл имеет минимум, а для кругосветного - нет. В общем случае можно утверждать только то, что интеграл имеет стационарное значение в смысле равенства нулю его первой вариации.

 

Следует осудить тенденцию авторов выводить все, даже очевидные вещи из далеко неочевидных общих принципов, притом не строгим образом. Характерным является следующий пример. Авторы не дают физического определения массы, из которого бы вытекало, что она всегда положительна. Масса определяется авторами, как множитель пропорциональности в функции Лагранжа свободной материальной точки. Ясно, что из такого определения ровно ничего не может следовать, так как на этот множитель попросту можно сократить. Между тем, авторы считают, что на основании такого определения можно из принципа наименьшего действия доказать положительность массы. При этом авторы понимают принцип наименьшего действия буквально, т.е. неверно, и это понимание является для них существенным. Мы охотно верим, что масса положительна, но никак не можем согласиться, что это вытекает из их рассуждений.»

 

 

Как видим, все эти замечания в той или иной форме повторяют те замечания, которые я неоднократно высказывал ранее к Механике Ландау (не будучи знаком с этой рецензией). Давайте я еще раз кратко сформулирую свои замечания.

1. ПНД в формулировке Ландау является глобальным, т.е. является общим принципом, когда действие на всем пути является минимальным, а на самом деле он является частным принципом для частных задач, где условия его применимости как минимального действия для каждой задачи определяются дополнительным расчетом кинетических фокусов, т.е. границ действительного пути, где действие остается минимальным.

2. ПНД не применим к любым системам, а только к идеальным системам и желательно с голономными связями и если в системе имеется диссипация энергии, то этот принцип не применим, но все реальные системы функционируют с диссипацией энергии, т.е. он практически не применим никогда.

3. Условия экстремальности действия на действительном пути Ландау даны не верно, т.к. равенство нулю первой вариации является только необходимым, но не достаточным условием экстремума (не говоря уже о минимуме как у Ландау, который, естественно, тоже не доказан).

 

 

Ну и что же сделал Ландау, чтобы устранить эти явные ляпы в своем учебнике. Да практически ничего. Давайте посмотрим, как он отреагировал на рецензию по сформулированным мною 3-м пунктам. Сразу скажу, что все замечания не остались не замеченными.

1-е замечание было отмечено в новой редакции учебника с одной стороны фразой на стр. 11 «Перейдем к выводу дифференциальных уравнений, решающих задачу об определение минимума интеграла (2.1)», которая подтверждает именно минимальность действия, а с другой стороны была сделана на стр. 10 сноска «Следует, однако, указать, что в такой формулировке ПНД не всегда справедлив для всей траектории в целом, а лишь для каждого из достаточно малых ее участков; для всей траектории может оказаться, что интеграл 2.1 имеет лишь экстремальное, не обязательно минимальное значение. Это обстоятельство, однако, совершенно несущественно при выводе уравнений движения, использующем лишь условие экстремальности.»

 

 

Здесь мы, во-первых, видим, что Ландау настаивает на том, что ему для вывода уравнений движения из ПНД нужна именно экстремальность этого принципа, а не стационарность, а, во-вторых, видим, что эта сноска не только не устранила недостаток ПНД связанный с его локальностью, а только запутала вопрос, т.к. совершенно не понятно как действие, обладая аддитивностью, может стать максимальным, если на всех локальных участках пути оно минимально. А следовало всего навсего написать, что «действие всегда имеет минимальное значение на локальном участке пути, т.е. до кинетического фокуса». Ведь, как пишет Полак в своей редакционной статье

«Еще Якоби показал, что если первая вариация простого определенного интеграла равна нулю, то вторая вариация интеграла может быть приведена к виду, удобному для исследования.

Опираясь на этом результате, Серре в нескольких мемуарах, напечатанных в 1871 – 1879 гг., решил вопрос о минимуме интеграла действия в общем виде, доказав, что вариация второго порядка интеграла действия для действительного движения положительна и минимум этого интеграла имеет место при некоторых ограничениях, наложенных на пределы интегрирования.»

 

 

А Лурье в своей Аналитической механике [7] пишет уже более конкретно

«1. Если в промежутке времени [t0, t1] определитель (20) не обращается в нуль (т.е. истинный путь не проходит через кинетический фокус), то действие по Гамильтону имеет минимум и существует единственное решение краевой задачи.

2. Если ∆(t1, t0) =0, то положения A0 и A1, проходимые в моменты t0 и t1, являются кинетическими фокусами и существуют другие бесконечно близкие пути, реализующие условие стационарности действия ; краевая задача имеет бесчисленное множество решений.

В вариационном исчислении условие (24) называют условием Якоби, а (29) – условием Лежандра. В задачах механики последнее оказывается требованием положительной знакоопределенности кинетической энергии и поэтому всегда соблюдается; условие Якоби выполняется на истинных путях, не проходящих через соответствующий начальному положению кинетический фокус.»

 

 

Таким образом 1-е замечание о локальности ПНД Ландау не устранено и, следовательно, по логике вещей дальнейшие издания этого учебника, построенного на глобальности ПНД, должны были быть запрещены, но, как мы видим, все произошло совсем не так. Как такое могло произойти – ума не приложу. Рискну только предположить, что своей великой идеей Ландау заразил и кого то из власть предержащих в науке. Но и в этом случае я не понимаю зачем Ландау лез на рожон именно с минимальностью действия, т.к. эта позиция очень уязвима. Ведь самое главное, что ему нужно было от ПНД это подведение теоретической базы под бессмысленный вывод уравнений движения из лагранжиана, а для этого было достаточно написать только о стационарности действия, т.е. о равенстве нулю первой вариации, которая позволяет обосновать для получения уравнений движения взятия производных от лагранжиана для получения уравнений Лагранжа. Но он упорно кругом пишет именно о минимуме действия на истинном пути. В таком случае рискну еще раз предположить, что именно довод о минимуме действия мог оказать влияние на власть предержащих в науке, а не какая то там стационарность, и, получив одобрение сверху на минимум, он так в наглую кругом и пишет именно о минимуме действия, не опасаясь никакой дальнейшей критики этого утверждения. Впрочем, это только мое предположение, а как оно там было на самом деле мы уже наверное не узнаем никогда. Однако, давайте рассмотрим и остальные замечания Фока-Юдина к учебнику Механики Ландау.

 

 

2-е замечание учтено, но очень странным образом. Например, по поводу диссипации энергии Ландау на стр. 97 заявил, что «Процесс движения в этих условиях уже не является чисто механическим процессом». Т.е. это уже не классическая механика и он за это не отвечает. Но позвольте, мы не знаем ни одной механической системы где бы отсутствовало трение, т.е. получается, что Механика Ландау не имеет никакого отношения к реальной механике. Единственная область, где, как пишет Фейнман, отсутствует трение это механика микромира и, таким образом, получается, что вся Механика Ландау нужна только для квантовой механики. Хотя и здесь не все так однозначно, т.к., например, тормозное излучение электрона, которое по сути является той же диссипацией энергии, никто вроде не отрицает. И получается, что и в квантовой механике Механика Ландау не применима. А тогда вообще не понятно о механике для какой галактики он написал свой учебник.

 

 

3-е замечание не осталось не замеченным, но реакция была чисто «еврейской».Фраза «Соответствующая задача нахождения функций, дающих экстремальные значения интегралу, решается операцией, носящей название варьирования»

заменена фразой

«Необходимым условием минимальности S является обращение в нуль совокупности этих членов; ее называют первой вариацией (или обычно просто вариацией) интеграла.»

Но ведь это опять ни коим образом не говорит о том, что при этом действие будет экстремально и тем более минимально. И хотя он теперь после фразы

«Это искомые дифференциальные уравнения; они называются в механике уравнениями Лагранжа» добавляет сноску о том, что

«В вариационном исчислении, рассматривающем формальную задачу об определение экстремумов интегралов вида (2.1), они называются уравнениями Эйлера»,

т.е. хочет нам заявить, что не только не претендует на приоритет получения уравнений Лагранжа из ПНД, но и то, что эти уравнения и получаются в вариационном исчисление при нахождение экстремалей, т.е. у него нет никаких противоречий с вариационным исчислением. Но это опять таки ни коим образом не является доказательством экстремальности функционала, когда первая вариация равна нулю, т.е. решение этих уравнений Эйлера служит нахождению экстремалей, но равенство нулю первой вариации так и остается только необходимым, но не достаточным условием экстремума функционала, а в формулировке ПНД, данной Ландау, надо найти даже не просто экстремум, а именно минимум.

 

 

Какой же вывод из реакции Ландау на замечания Фока по ПНД, которые практически досконально совпали и со сделанными мною замечаниями, можно из этого сделать. Да, первоначально я придерживался того же вывода, что и Фок, т.е. о том, что просто Ландау плохо разобрался в вариационном исчисление и, следовательно, в вариационном принципе наименьшего действия, но сейчас я больше склоняюсь к другому выводу, который считаю более важным, хотя при этом и первый вывод имеет место быть. Так вот, сейчас я считаю, что, т.к. Ландау поставил перед собою великую цель построения всей физики исходя из ПНД, то и все свои действия он подчинял этой великой идее, а посему все, что мешало этому, не имело для него никакого значения, т.к. его учение, которое является единственно верным, не может не быть таковым при любых происках врагов. Т.е. для него ПНД был не просто один из принципов механики, а гораздо большее. И как писал Розенфельд «Ландау играл на этой скрипке Энгра, веря в то, что всю физику можно вывести из одного замечательного принципа наименьшего действия» (для справки - скрипка Энгра это французская идиома, означающая любимую игрушку, не имеющую отношения к основной профессии или иногда переводится как хобби).

 

 

И Ландау с этой своей идеей (игрушкой) дошел до такой глупости, что стал даже определять понятие такой фундаментальной величины в физике как масса из каких то там свойств полученной им буковки в функции Лагранжа. Конкретно на стр. 16 [2] он пишет «...т.е. функция Лагранжа в рассматриваемом случае прямо пропорциональна квадрату скорости : L=a*v^2. ... Постоянную a принято обозначать как m/2 ... Величина m называется массой материальной точки.» (в последнем издание буковку a убрали). А затем он из ПНД, т.е. именно из наименьшего действия, доказывает нам, что эта буковка m не может быть отрицательной. Таким образом, для Ландау вся физика, как для типичного математико-физика, просто подопытный кролик, на котором он может продемонстрировать свои математические способности, т.к. в математике это сделать становится очень сложно. Ведь еще Лагранж писал, что математикам пора перебираться в другие разделы наук. Вот, что он написал в письме к Даламберу [10]

«Я думаю также, что шахта становится слишком глубокой и что ее придется рано или поздно бросить, если не будут открыты новые рудоносные жилы. Физика и химия представляют ныне сокровища, гораздо более блестящие и более легко эксплуатируемые; таким образом, по-видимому, все всецело обратились в эту сторону, и возможно, что места по геометрии в Академии наук сделаются когда-нибудь тем, чем являются в настоящее время кафедры арабского языка в университетах.»

 

 

И действительно, математики, которым стало делать нечего в математике, набросились на физику и в основном на ее главную часть механику и, естественно, после этого любвеобильные математики задушили в своих объятиях всю физику. А Ландау, чтобы демонстрировать на полных основаниях свои математические познания в физике, во введение к тому Механики делит всю физику на экспериментальную, теоретическую и математическую. Естественно, он будет заниматься теоретической физикой, а в ней очень важную роль играют приближенные вычисления, которыми он только и занимается, т.е. он будет решать приблизительные задачи с приблизительным решением. Конкретно он пишет

«Таким образом приближения играют очень важную роль в общих физических законах. Не менее велика, однако, их роль и при выводе из общих теорий конкретных физических законов. Слишком точные вычисления с учетом несуществующих факторов не только бесплодны и излишне усложняют результаты расчета, но могут даже привести к тому, что существующие в данном явление закономерности вообще выпадут из рассмотрения.»

Здесь правда надо заметить, что в издание 1958 года все эти его графоманские рассуждения о трех различных физиках, которые были во введении, додумались все таки убрать (вместе с самим введением).

 

 

А по поводу его высказывания надо сделать некоторые пояснения. Вообще то, точным, обычно считается аналитическое решение задачи, а приближенным - решение ее численными методами, но Ландау здесь говорит совершенно о другом. Наличие в дифференциальных уравнениях нелинейных элементов делает такие дифференциальные уравнения не решаемыми аналитически, но с помощью различных ухищрений их иногда можно решить аналитически приблизительно. Так вот Ландау как раз и является специалистом по приблизительному решению приблизительных, т.е. не реальных, задач и по этому он и заявляет, что теоретическая физика должна заниматься именно этим. И рассматривая задачи, например, на стр.81 [3] он неоднократно пишет «При x<<l имеем....», «В этом случае удлинение пружины (при φ<<1)...», «При φ<<1 из полученной...», т.е. он решает не реальную задачу, а немножко похожую на реальную. При этом, он свои приблизительны методы решения задач переносит и на чисто теоретические выводы и, например, на стр.47 [4] он пишет

«Для осуществления этого перехода разложим L в ряд по степеням v/c. Тогда, опуская члены высших порядков, получаем: L= -a*c*sqrt(1-v^2/c^2) ≈ -a*c + a*v^2/(2*c).»

Возьмем для примера a=1, v=290000 км/с, c=300000 км/с и получаем

-a*c*sqrt(1-v^2/c^2) = -76,81

-a*c + a*v^2/(2*c) = -159,83

 

 

Таким образом, и все его теоретические выводы тоже являются приближенными. При этом, например, рассматривая движения тел в среде, он, хоть и не считает такие задачи механическими, все же отводит им шесть параграфов в своей механике (25...30), по одной простой причине. Для частного случая, когда сопротивление среды пропорционально скорости в первой степени, оказывается дифференциальные уравнения, хотя и не получаются из его любимого ПНД, но они получаются линейным, а в этом случае он их может решить и, следовательно, этому он и будет учить своих читателей. Правда здесь опять таки при вынужденных колебаниях и если жесткость не линейная то не во всех случаях он может решить эти уравнения даже приблизительно, но целых шесть параграфов то написано. Таким образом, и трение, по большому счету, не является препятствием для отнесения таких систем к механическим, т.е. механикой у Ландау являются только те процессы при описание которых он может продемонстрировать свои математические способности. А вот, когда он рассматривает различные механические системы, где всегда присутствует в основном сухое трение (или скольжения или качения), то он на стр.162 объявляет эти системы уже точно не механическими (такие уравнения не решаются аналитически) и по этому дальше он будет учить читателей решать только механические задачи, т.е. получается что он будет учить решать приблизительные (учебные) механические задачи, где сухого трения нет.

 

 

Вот его обоснование такого подхода

«Если при скольжение трение настолько мало, что им можно вовсе пренебречь, то поверхности тел называются абсолютно гладкими. Напротив, если свойства поверхности допускают лишь чистое качение тел без скольжения, а трением при качение можно пренебречь, то поверхности называются абсолютно шероховатыми.

В обоих случаях силы трения не фигурируют явным образом в задаче о движении тел, и по этому задача является чисто механической. Если же конкретные свойства трения существенны для движения, то последнее не является уже чисто механическим процессом (ср. §25).»

А теперь упритесь большим пальцем правой руки в абсолютно гладкий стол и быстро проведите рукой справа налево. У вас возникнут автоколебания большого пальца, но Ландау не научит Вас решать эту элементарную механическую задачку потому, что по его классификации это не механическая задача. Да, Ландау в совершенстве владел интегральным и дифференциальным исчислениями и здесь рядом с ним можно поставить разве что Эйлера и Лагранжа, но объявлять механикой только те явления, которые описываются дифференциальными уравнениями, вытекающими из ПНД, т.е. обязательно без трения, и которые он может решить, в корне не верно.

 

 

Таким образом, мы опять видим, что для Ландау ПНД это не просто любимая игрушка, но и великая идея, которой подчинено все изложение курса теоретической физики, а такие идеи обычно подчиняют себе разум ее творцов. Да, великую идею Ландау нельзя сравнивать с великими идеями построения Третьего Рейха в Германии или коммунизма в СССР, но то, что делают великие идеи подчиняя себе разум их творцов мы прекрасно видели на этих примерах. По этому, бесполезно было ожидать, что Ландау внемлет разуму и откажется от своей великой идеи. В связи с этим у меня никак не укладывается в голове, как мог Ландау на конференции по теории элементарных частиц в Киеве в 1959 году заявить, что гамильтониан мёртв и должен быть похоронен со всеми подобающими ему почестями. Но ведь, если хоронить гамильтониан, то это значит похоронить и его папу, т.е.  лагранжиан, и весь его Курс построенный на лагранжевом (гамильтоновом) формализме. И хотя это заявление касалось только теории элементарных частиц, но ведь он то проповедовал идею о том, что ПНД всесилен во всех разделах физики. На всякий случай, во избежание обвинений в том, что я что то не так понял в его выступление, приведу цитату из его выступления на этой конференции [31].

 

 

«Операторы, содержащие ненаблюдаемую информацию, должны исчезнуть из теории, и, поскольку гамильтониан можно построить только из операторов, мы с необходимостью приходим к выводу, что гамильтонов метод в квантовой механике изжил себя и должен быть похоронен, конечно, со всеми почестями, которые он заслужил.

Основой для новой теории должна служить новая диаграммная техника, которая использует только диаграммы со «свободными» концами, то есть амплитуды рассеяния и их аналитические продолжения. Физическую основу этого аппарата образуют соотношения унитарности и принцип локальности взаимодействия, который проявляется в аналитических свойствах фундаментальных величин теории, например в различного рода дисперсионных соотношениях.

Поскольку такая новая диаграммная теория еще не построена, мы вынуждены находить аналитические свойства вершинных диаграмм, исходя из гамильтонова формализма. Однако нужно быть очень наивными, чтобы пытаться придать «строгость» такому выводу; нельзя забывать, что мы получаем реально существующие уравнения из гамильтонианов, которые в действительности не существуют.»

 

 

Быстрее всего и после этого Ландау не изменил бы своего отношения к ПНД как к великой идее, но мы этого уже никогда не узнаем, т.к. в 1962 году он попал в автомобильную аварию, после которой так и не восстановился как ученый и которая в конце концов и стала причиной его смерти в 1968 году, и все последующие издания его Курса выходили уже без него. Но научные хунвейбины и после его смерти, вооружившись цитатником великого Дау, продолжают стучать им как дубиной по головам всем кто не согласен с великой идеей великого Дау. Хотя не задолго до смерти Ландау [20] написал: «…Основные представления о пространстве и времени, а также основные законы, которые мы до сих пор считали несомненными, в чем-то нехороши. Где-то в фундамент науки надо внести поправки». Подобные мысли высказывали и Эйнштейн и Фейнман и многие другие ученые забравшиеся на гребне революционной волны на вершину славы. Например, о квантовой механике Эйнштейн [11] сказал "Большие первоначальные успехи теории квантов не могли меня заставить поверить в лежащую в ее основе игру в кости... Физики считают меня старым глупцом, но я убежден, что в будущем развитие физики пойдет в другом направлении, чем до сих пор". И по поводу своей ОТО он тоже сомневался в ее правильности [12] "Я считаю вполне вероятным, что физика может и не основываться на концепции поля, т.е. на непрерывных структурах. Тогда ничего не останется от моего  воздушного замка,  включая теорию тяготения, как, впрочем, и от всей современной физики".  Но, как мы понимаем научные хунвейбины, т.е. последователи этих революционеров в физике, и не собираются вносить никаких поправок, т.к., во-первых, они просто не в состоянии этого сделать, а, во-вторых, если это сделать, то они потеряют власть в науке, т.к. все их научные достижения окажутся ложными.

 

 

Однако, мы с Вами в истории ПНД, предшествующей написанию курса физики Ландау, упустили из рассмотрения два важных события произошедших в физике и без которых история о ПНД не может быть полной. Но, прежде чем перейти к этим историческим событиям, давайте рассмотрим один интересный момент. Возвращаясь к моему комментарию по поводу реакции Ландау на первое замечание, напоминаю, что Ландау должен был знать, что решение краевой задачи имеет единственное решение, только, если мы рассматриваем ее с точки зрения ПНД на локальном участке пути, т.е. задача не имеет единственного общего решения, но он на стр. 183 [3] пишет 

«Принципом наименьшего действия движение механической системы определяется полностью: путем решения следующих из этого принципа уравнений движения можно найти как форму траектории, так и зависимость положения на траектории от времени. Если ограничится более узким вопросом об определении лишь самой траектории (оставляя в стороне временную часть задачи), то оказывается возможным установить для этой цели упрощенную форму принципа наименьшего действия»

 

 

Как Вы поняли упрощенная форма это ПНД1, но здесь надо заметить, что решая задачу с использованием ПНД мы решаем и не краевую задачу и не задачу вариационного исчисления. Хотя поясню, что, по некоторой аналогии с прямой и обратной задачей динамики, можно аналогично и задачу с использованием ПНД считать или вариационной задачей (задачей управления) или краевой задачей, но все равно задача на применение ПНД не вписывается ни туда ни туда. К краевой задаче она не относится т.к. у нас кроме некоторых начальных условий в двух точках задан еще некий функционал, т.е. явный признак вариационной задачи, но с другой стороны этот функционал нам не надо минимизировать, т.к. у нас априори дано, что при свободном движении этот функционал и так будет минимальный. Таким образом, если это вариационная задача, то не понятно какую функцию X(t) или U(t) (для задач механики это будут функции сил) в ней искать, если эти функции нам не нужны из смысла ПНД. По этому, я так и не понял как нам использовать ПНД, чтобы найти единственную истинную траекторию в первой задаче и зачем он нужен во второй задаче, которые рассмотрены в статье Слудского [28], с движением тела в простейшем плоском поле постоянной напряженности, т.е. в поле плоского конденсатора. Впрочем, если мы рассматриваем упрощенное движение тела, то можем принять, что и в локальном поле тяготения Земли при движение по двум координатам будет осуществляться по уравнениям X=V0*cos(alfa)*t,   Y=V0*sin(alfa)*t - g*t^2/2 , если принять g=const . В этом случае подынтегральные выражения для ПНД1 и ПНД2, т.е. функционалы будут

 

 T      = m*(V0^2 -2*V0*g*t*sin(alfa) +g^2*t^2)/2

 T-U =m*(V0^2-4*V0*g*t*sin(alfa)+2*g^2*t^2)/2.

 

 

Допустим у нас заданы начальная точка А(0;0) и конечная точка В(80;0) и надо найти истинную траекторию по критерию T, когда задана начальная скорость V0=30 м/с и по критерию T-U, когда задано время движения до точки В равное 3,123 секунды. При этом примем, что ускорение свободного падения g=10  м/с^2. Чтобы однозначно определить траекторию движения нам в первой задаче надо найти угол alfa , чтобы определить скорости по осям X и Y, а во второй задаче надо найти не только угол alfa чтобы определить скорости по осям X и Y, но и саму скорость V0. И двух уравнений движения по осям X и Y нам для этого вполне достаточно. Математический пакет Maple справляется с этими системами уравнений без проблем и для первой задачи у нас будет

 

> restart;

> g:=10.0:V0:=30.0:

> eqns:={V0*cos(a)*t=80.0,V0*t*sin(a)-g*t^2/2=0.};

> solve(eqns,{a,t});

а для второй задачи

 

> restart;

> g:=10.0:t:=3.123:

> eqns:={V0*cos(a)*t=80.0,V0*t*sin(a)-g*t^2/2=0.};

> solve(eqns,{a,V0});

 

Как видим, для второй задачи начальные условия определены однозначно, т.к. скорость -30 м/с и угол -2,59 рад явно не являются решением задачи, и здесь никакой ПНД2 для нахождения единственной истинной траектории не нужен, т.е. зачем он нужен. Правда, как будет показано ниже при решение задачи Фейнмана, когда движение осуществляется в реальном поле тяготения Земли и на рис 3, когда движение осуществляется в поле 2-х зарядов, решений опять таки будет как минимум два. А вот в первой задаче у нас уже сейчас получились два реальных решения t=3,123; alfa=0.547 и t=5,123; alfa=1.023 и возникает другой вопрос - а как можно используя ПНД найти единственное решение в первой задаче. Ведь действительно действие при движение когда alfa=0.547 (S=1151,3) явно меньше чем действие при alfa=1,023 (S=1184,3), но как при этом использовать выражение для функционала, чтобы найти единственное решение, Ландау нигде не пишет. Правда, тут возникает и другой вопрос - а почему оно должно быть единственным, если оба решения реальные и движение по обоим путям является прямым, т.е. не окольным. Но попробуем все-таки как то использовать выражение для расчета действия. Ведь, если на прямом пути действие минимально или экстремально, то, взяв от него производную, мы можем получившееся выражение приравнять нулю и получим еще одно уравнение для нашей задачи. Возьмем интеграл от T  по времени от t1=0 до t2=2*V0*sin(alfa)/g

 

 S = m*(V0^3*sin(alfa) *(1-2*sin(alfa)^2/3))/g/2

 

Теперь уберем из этого выражения лишние константы m, g и двойку и возьмем производную по alfa

 

 dS/dalfa = V0^3*cos(alfa) *(1-2*sin(alfa)^2)

 

Добавим это уравнение в нашу систему уравнений и заставим Maple решить уже эту систему уравнений.

 

> restart;

> g:=10.0:V0:=30.0:

 

> eqns:={V0*cos(a)*t=80.0,V0*t*sin(a)-g*t^2/2=0.,V0^3*cos(a)*(1-2*sin(a)^2)/g};

> solve(eqns,{a,t});

> 

 

Как видим, Maple отказывается решать эту систему уравнений. Значит она не имеет решения по тому, что эти уравнения не совместимы, т.е. уравнение, где производная от действия равна нулю не имеет никакого отношения к уравнениям движения, а, следовательно, и само действие никак не связано с уравнениями движения. Тогда поступим иначе. Заставим Maple просто решить только одно уравнение с производной от действия.

 

> restart;

> S:=V0^3*sin(a)*(1-2*sin(a)^2/3);

> proizv:=factor(diff(S,a));

> V0:=30.0:

> eqns:={proizv=0.};

> solve(eqns,{a});

 

Это уравнение имеет решения, но теперь уже целых пять, вместо четырех, что у нас были. Вот только беда. Ни одно из этих решений не совпадает ни с одним решением краевой задачи, полученными нами ранее. По этому, выделить один прямой путь из получившихся у нас двух путей не получается и в этом случае, а никаких других вариантов выделить один путь из двух я не вижу. При этом, ПНД в поле плоского конденсатора соблюдается глобально и по этому мы даже не можем заявить, что конечная точка лежит за кинетическим фокусом, т.е. что мы и не вправе требовать от ПНД единственного решения. Но может быть в ПНД2 выражение для действия как то связано с уравнениями движения и при решение краевой задачи с избыточным условием равенства нулю производной от действия это никак не отразится на решении.

 

> restart;

> g:=10.0:t:=3.123:

 

> eqns:={V0*cos(a)*t=80.0,V0*t*sin(a)-g*t^2/2=0.,-V0^3*cos(a)*(2*sin(a)-1)*(2*sin(a)+1)/g=0.};

> solve(eqns,{a,V0});

>

 

Как видим, Maple и здесь отказывается решать эту систему уравнений. Значит и она не имеет решения по тому, что и эти уравнения не совместимы, хотя одно уравнение с производной Maple опять решает без проблем.

 

> restart;

> S:=V0^3*sin(a)*(1-4*sin(a)^2/3)/g;

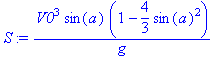
> proizv:=factor(diff(S,a));

> g:=10.0:V0:=30.0:

> eqns:={proizv=0.};

> solve(eqns,{a});

 

У нас опять, как и с ПНД1 получилось решений пять, но опять ни одно из них не совпало с тем, что было при решении краевой задачи. Правда, ответ a=0.5236 очень похож на решение краевой задачи a=0.5474 и может быть это расхождение получается вследствие приближенного решения. Давайте это проверим на решение этой же задачи, когда абсцисса конечной точки будет 40 метров, а время движения 2,8284 сек.

 

> restart;

> g:=10.0:t:=2.8284:

 

> eqns:={V0*cos(a)*t=40.0,V0*t*sin(a)-g*t^2/2=0.};

> solve(eqns,{a,V0});

 

И опять найдем решение от производной равной нулю

 

> restart;

> S:=V0^3*sin(a)*(1-4*sin(a)^2/3)/g;

> proizv:=factor(diff(S,a));

> g:=10.0:V0:=20.0:

> eqns:={proizv=0.};

> solve(eqns,{a});

 

 

Ну, теперь то уж точно видно, что ни одно из этих решений не похоже на a=0.7854. Более того, эти решения получились те же самые, что и при V0=30 м/с. Впрочем, этого и следовало ожидать, т.к. в уравнение с производной на V0 можно просто сократить и по этому ответ будет всегда один и тот же. Вот только он никогда не совпадет, как и у ПНД1, с реальными решениями этой краевой задачи. И, следовательно, ни в ПНД1 ни в ПНД2 их функционалы (подынтегральные выражения определяющие действие) никоим образом не связаны с определением истинных путей, а попросту говоря никак не связаны с реальными уравнениями движения даже в том случае, когда действие имеет экстремальное значение (при этом оно конечно же имеет и стационарное значение). Т.е. получается, что для нахождения уравнений движения, сам ПНД его сторонникам абсолютно не нужен, а отстаивают они его применение в механике только по одной простой причине. Он позволяет им подвести теоретическую основу под бессмысленный вывод уравнений движения из не менее бессмысленного лагранжиана, который является специально подобранным математическим выражением, не имеющим никакого физического смысла. И на примере решения простейших задач мы видим полную беспомощность ПНД как принципа механики, который, будучи таковым, обязательно должен бы был влиять на определение траектории движения тела, которая в наших задачах определяется начальными условиями.  

 

 

Таким образом, и во 2-ой краевой задаче, если будет несколько решений, ПНД2 никак нам не поможет найти единственное решение, т.е. ПНД2 тоже не сможет однозначно определить траекторию свободного движения тела. Рассмотрим движение нашего тела уже не в поле одного другого неподвижного тела, т.е. в монополе, а в полях сразу от двух тел, т.е. уже в мультиполе. На рис.1 и рис.2 Вы как раз и видите траектории движения тела с отрицательным зарядом из точки А в точку В в поле тяготения двух других положительных зарядов. При этом мы видим, что теперь уже разнообразие свободных путей становится просто огромным и у нас появляется возможность теперь уже сравнить не один прямой путь с несколькими окольными, как это обычно делается, а наоборот один окольный путь с несколькими прямыми. Например, я взял наугад один из окольных путей (по дуге окружности- красная кривая) и хочу сравнить действие на этом пути со свободными путями различной конфигурации, т.к. в точке А начальная скорость частицы на свободном пути может быть любая. И при получившемся при этом времени движения в точку В мы и будем сравнивать этот прямой путь с окольным. Как сами рисунки, так и данные в таблицах 1 и 2 я привожу из своей предыдущей статьи о ПНД [21], где я их получил, используя программу Hrono1 (скачать программу можно здесь http://modsys.narod.ru в разделе Программы). Сейчас я выложил уже 2-ю версию программы Hrono, с которой гораздо удобнее работать, а после загрузки программы у Вас автоматически загрузятся все начальные данные для расчета при движение по одному из путей (синяя кривая), а для других путей я приведу дополнительные исходные данные в таблице 1.  

 

 

 

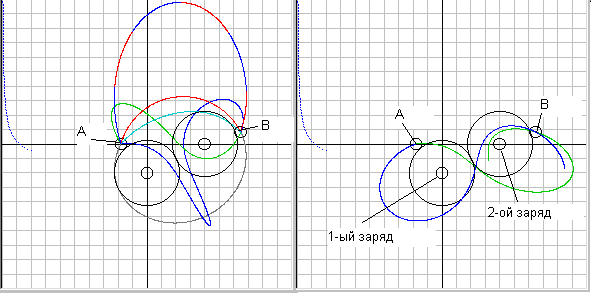
Рис.1 Несколько траекторий движений тела по свободным путям и одна траектория по  несвободному пути (по дуге окружности – красная кривая) в мультиполе ))var2-

Рис.2 Траектории свободного движения двух тел в мультиполе ))var2- , где они не только достигают конечной точки за одно и тоже время, но и их начальные скорости равны (V1=V2=15,811 м/с).

 

 

Табл.1

		t	mV	T-U	T	T+U
Xn=-9,Xk=32,4        Yn=0,Yk=4,14    X40=12,5 q1=q2=0,0005 k           P0=0,01 сек	Синяя кривая    5(Vx=13,025;Vy=2,0)	10,03	1701,3	-750,95	850,64	2452,2
	4(Vx=3,504;Vy=12,703)	5,20	568,55	-702,48	284,25	1271,0
	4(Vx=2,782;Vy=10,085)	10,03	353,19	-1776,1	176,57	2129,2
	Коричневая кривая 5(Vx=-8,0;Vy=-15,15)	5,75	1318,4	-432,09	659,18	1750,5
	4(Vx=4,468;Vy=16,199)	3,54	821,15	-256,56	410,55	1077,7
	4(Vx=3,316;Vy=12,023)	5,75	518,19	-835,18	259,07	1353,3
	Синяя+красная кривая   5 (Vx=-5,6;Vy=17,8)	14,27	1119,6	-3614,7	559,81	4734,3
	4(Vx=4,961;Vy=17,988)	3,18	913,10	-142,05	456,53	1055,1
	4(Vx=2,708;Vy=9,817)	14,27	319,89	-2668,4	159,92	2988,2
	Желто-зеленая кривая 5(Vx=-7,0;Vy=12,13)	5,98	1084,3	-444,99	542,15	1529,3
	4(Vx=3,724;Vy=13,5)	4,70	623,67	-578,05	311,81	1201,7
	4(Vx=3,251;Vy=11,787)	5,98	499,82	-889,62	249,88	1389,4
	Сиреневая кривая        5(Vx=13,0;Vy=15,0)	2,28	951,25	142,57	475,61	808,64
	4(Vx=5,278;Vy=19,134)	2,95	982,99	-63,49	491,47	1046,4
	4(Vx=6,607;Vy=23,954)	2,28	1271,0	207,13	635,49	1063,9

 

 

Как видно из данных табл. 1, успехи у ПНД, как у глобального принципа, даже когда мы ему дали фору, не важные, т.е. выиграно только 3 партии из 10 (2 раза выиграл ПНД2 по критерию T – U – сиреневая и сяняя+красная кривые и 1 раз ПНД1 по критерию T и mV- сиреневая кривая). Защитникам ПНД при таких результатах остается только сказать, что во время проведения вычислительных экспериментов у них ПНД немного приболел, но, когда он выздоровеет, он еще покажет хорошие результаты. Вот только я надеюсь, что после этой статьи он уже не выздоровеет никогда. Но даже, если ПНД поправится и покажет более приличный результат, это не снимает вопроса, который мы сейчас рассматриваем – какой же путь из нескольких свободных путей выбирать, если у нас на обоих прямых путях будет одинаковым время движения. Такой пример у нас будет, когда мы будем рассматривать задачу Фейнмана, где конечную точку мы поместим явно за кинетическим фокусом. Но и здесь, когда у нас имеются только по одному свободному пути при разном времени движения тела из точки А в точку В я, например, затрудняюсь, используя ПНД и заданное время движения, однозначно определить уравнения движения и начальные скорости в этих примерах. А, т.к. сторонники ПНД утверждают, что для этого минимальность действия им не нужна, а достаточно использовать только стационарность ПНД, вот пусть и найдут уравнения движения и начальные скорости для свободных путей из табл. 1, а я в следующей редакции статьи опубликую их решения этих краевых задач. Вот только я уже сейчас предполагаю, что все решения у них (если получатся), то будут похожи на красно-синюю или сиреневую траектории.

 

 

А сейчас давайте рассмотрим убийственный случай, когда у нас на двух прямых (истинных) путях будет не только время движения одинаковое, но и начальная скорость будет одинаковая, т.е. применимы и ПНД1 и ПНД2. Такие две траектории представлены на рисунке 2. Так какой же из этих двух путей прямой, а какой окольный, т.е. на каком пути у нас не свободное движение и для какого же пути Ландау обещал найти уравнения движения, которые выделят нужную форму траектории. Я на эти вопросы ответа не нахожу. А сторонники ПНД, если и найдут решение этой задачи, то оно у них будет совершенно другим, т.е. форма траектории будет так же похожа на красно-синюю или сиреневую траектории на рис.1. И единственный вывод, какой можно сделать из этого примера – это изобрести принцип одинакового действия, т.е. если на двух истинных путях полное действие, т.е. интеграл от T + U по времени, одинаковое, то и начальные скорости и время движения в этих путях будут одни и те же. Вот только не понятно кому нужен еще и этот интегральный принцип. Да, и в этом примере сторонники ПНД могут заявить, что конечная точка лежит за кинетическим фокусом, а в таком случае ПНД не применим, как требующий минимума действия, по этому ничего требовать от него, кроме стационарности, нельзя. Но ведь Ландау построил весь свой курс именно на глобальном применении ПНД, т.е. для всей траектории, а не на локальном участке пути, и использовал его как принцип, требующий именно минимума действия. И, исходя из этого, он заявлял, что ПНД позволяет однозначно найти форму этой траектории. Как видим, Ландау здесь был не прав и, следовательно, весь его курс теоретической физики построен на песке.

 

 

Табл. 2

		t	mV	T- U	T	T+U
Xn=-9,Xk=32,4        Yn=0,Yk=4,14 q1=q2=0,0005 k           P0=0,0005 сек	Желто-зеленая кривая 5(Vx=15,6844;Vy=2,0)	7,301	1187,7	-876,00	593,87	2063,7
	Синяя кривая 5(Vx= -15,0218;Vy=-4,9341)	7,301	1639,0	-424,73	819,50	2063,7

 

 

 

А теперь давайте вернемся к истории ПНД. Когда Планк заявлял о том, что ПНД не оказал никакого влияния на науку, то это, естественно, относилось к периоду до открытия им кванта действия, т.к. после этого не только опять вспомнили о ПНД, но и появились революционные теории – квантовая механика и релятивистская механика. А связано это было с тем, что найденная им константа h в его статистическом распределение энергии излучения абсолютно черного тела имела размерность действия, т.е. Дж*с. Хотя сам Планк, когда подгонял свое статистическое распределение под экспериментальные данные ни о каком действие и ни о каких квантах и не задумывался. У него по задумке это была элементарная область вероятности, но в тексте он кругом пишет, что h это просто константа. А, как я показал в своей статье [24] из остатков логики Планка более правдоподобно считать, что это энергия излученная за одно колебание в секунду. У Планка это были колебания молекул газа, но более правдоподобно считать, что это колебания электрона при его вращение вокруг ядра.

 

 

А свое название «кванта действия» эта константа получила после того как Эйнштейн ввел понятие фотона с его квантом энергии в своей теории фотоэффекта. И величина кванта энергии у него совпала с величиной порции энергии, которой оперировал Планк в своей формуле, где величина этой порции тоже определялась формулой h*v, где v это частота колебаний. Отсюда естественно предположить, что и h является квантом чего-то, а т.к. размерность этой константы совпала с размерностью действия, то ее и стали называть квантом действия. Вот так действие вновь всплыло на исторической арене после некоторого забвения, а вместе с самим понятием действия всплыл и ПНД, но прижился он только в новых революционных теориях. Например, в статье «Принцип Гамильтона и общая теория относительности» Эйнштейн подтверждает, что все его уравнения ОТО можно получить из вариационного принципа Гамильтона, что он и делает, т.к. на момент написания статьи он уже знает какие уравнения надо получить из ПНД, т.к. 18 ноября 1915 года он их уже украл у Д.Гильберта. Вот только, как пишет А.Тяпкин [39]

 «Но есть серьезные основания сомневаться в возможности самостоятельно справиться Эйнштейну с математической проблемой вывода фундаментальных уравнений, если, даже располагая материалами Гильберта, он смог овладеть выводом их из вариационного принципа лишь к концу следующего года. Как отмечает Пайс, только Гильберт, в отличие от Лоренца и Эйнштейна, владел тогда умением правильно записывать необходимое соотношение для вариационного принципа ([30], с. 250).»

А, если к этому добавить, что свою статью Эйнштейн писал, когда и Г.Лоренц и Д.Гильберт уже опубликовали в 1915-1916 годах свои выводы из ПНД нужных ему уравнений, то становится совершенно ясно, что Эйнштейн к математической части своей чисто геометрической теории, т.е. к ОТО, не имеет никакого отношения. Впрочем, как и к выводу из этой теории формулы для аномального смещения перигелия Меркурия, т.к. эту формулу Эйнштейн украл у П.Гербера [40].

 

 

Но для нас будет более интересно посмотреть как Ландау получает уравнения ОТО в своей теории поля [4], которая, как я уже писал, была закончена им до написания 1-го тома его Курса, т.е. до Механики. Здесь Ландау не вникает в подробности минимума или экстремума действия, а просто пишет (см. стр.109)

«уравнения движения (т.е. уравнения поля, если речь идет о каком-либо поле) получаются согласно принципу наименьшего действия путем варьирования S»

и приравнивает нулю первую вариацию действия. Таким образом, здесь он фактически использует только стационарность действия. Но вот в §8, с которого начинается изложение релятивистской механики, он уже пишет более конкретно (см. стр. 43)

«При исследовании движения материальных частиц мы будем исходить из принципа наименьшего действия. Этот принцип заключается в том, что для всякой механической системы существует такой интеграл S, называемый действием, который для действительного движения имеет минимум и вариация δS которого, следовательно, равна нулю.»

Очень интересный поворот. Оказывается, что здесь у него уже не действие имеет минимум, по тому, что вариация равна нулю, а наоборот вариация равна нулю, по тому, что действие на истинном пути минимально, т.е. теперь у него получается, что ветер дует, потому что деревья качаются.

 

 

А в самом низу стр.43 фантазия Ландау просто разбушевалась и он пишет

«Действительно, мы видели в §3, что интеграл ∫ds имеет максимальное значение вдоль прямой мировой линии; интегрируя вдоль кривой мировой линии, можно сделать его сколь угодно малым.

Таким образом, интеграл, взятый с положительным знаком, не может иметь минимума; взятый же с обратным знаком он имеет минимум – вдоль прямой мировой линии.»

Интересно было бы посмотреть где это он доказал, что минимальное и максимальное значения действия симметричны относительно нуля, чтобы делать такие выводы. Ведь, если максимум действия на конкретном пути между двумя точками равен +10, то минимум на других путях может быть равен и нулю и +1 и -20, но не обязательно -10.  Таким образом, мы видим, что если в механике Ландау просто путался с ПНД, то в теории поля он окончательно с ним запутался. Однако, его последователи искренне веруют во все, что он написал, и не терпят никаких поползновений на его великую идею.

 

 

Но может быть в релятивистской форме этот принцип действительно существенно отличается от классической формы и на действительном пути замедление времени от гравитации и скорости движения будет действительно минимальным. Давайте проверим это на примере конкретной задачи Фейнмана, которую он в своей книге [25] как раз и сформулировал для проверки справедливости ПНД в релятивистской форме.

«Ту же самую шутку я проделал четыре года спустя в Принстоне, разговаривая с опытным физиком, ассистентом Эйнштейна, который все время работал с гравитацией. Я дал ему такую задачу: вы взлетаете в ракете с часами на борту, а другие часы остаются на земле. Задача состоит в том, что вы должны вернуться, когда по земным часам пройдет ровно один час. Кроме того, вы хотите, чтобы ваши часы за время полета ушли вперед как можно больше. Согласно Эйнштейну, если взлететь очень высоко, часы пойдут быстрее, потому что, чем выше находишься в гравитационном поле, тем быстрее идут часы. Однако если вы попытаетесь лететь слишком быстро, а у вас только час в запасе и вы должны двигаться быстро, чтобы успеть вернуться, то ваши часы из-за большой скорости замедлятся. Поэтому вы не можете лететь слишком высоко. Вопрос сводится к следующему: по какой программе должны меняться скорость и высота, чтобы обеспечить максимальный уход вперед ваших часов? Ассистент Эйнштейна довольно долго работал над этой задачей, прежде чем понял, что ответ - это просто свободное движение материи. Если вы выстрелите вверх так, что время, необходимое снаряду, чтобы пролететь и упасть, составляет ровно час, это и будет правильное движение. Это – фундаментальный принцип эйнштейновский гравитации, гласящий, что для свободного движения собственное время максимально. Но когда я поставил задачу в такой форме - ракета с часами - физик не узнал этого закона.»

 

 

Вообще то это типичная вариационная задача и нам предлагается найти две управляющие функции V(t) и H(t), которые обеспечат максимальное значение функционала определяющего убыстрение хода часов или минимальное их замедление от двух факторов – высоты полета H и скорости полета V. Но исходя из того, что есть принцип наименьшего действия нам предлагают не решать эту задачу, а поверить, что при движение по действительному, т.е. свободному, т.е. прямому пути у нас будет не только минимальное значение функционала определяющего действие по ПНД2 в классической форме, но и поверить тому, что при движение по такому пути у нас как раз и будет минимальное замедление времени на часах в ракете, т.е. максимальное ускорение их хода. Таким образом, ответом будет свободное движение ракеты без всякого управления, но при этом ракетой надо выстрелить с какой то начальной скоростью, т.е. просто рассмотреть движение снаряда. При этом Фейнман рассматривает только частный случай вертикального движения снаряда, где замедление времени в течение 1 часа полета действительно будет минимальным, т.е. ускорение времени dt=8,87-2,69= 6,17 *10^-7 с. Здесь первая цифра убыстрение хода часов при уменьшение гравитации на высоте H, а вторая цифра это замедление времени от увеличения скорости V. Вот только Фейнман здесь немного слукавил и рассмотрел движение тела в частном поле тяготения Земли, когда оно близко к полю плоского конденсатора или к локальному полю тяготения Земли, а в этом случае, как мы выяснили в первой статье, ПНД соблюдается в классической формулировке глобально. По этому, можно предположить, что и здесь, если точка взлета и приземления одна и та же, то, как не управляй скоростью движения, результат будет хуже, чем у Фейнмана.

 

 

Но из задачи Фейнмана многие могут сделать общий вывод, о том, что и когда возможно движение не только по вертикали, но и по горизонтали с приземлением через час в произвольную точку, то исходя из релятивистского ПНД убыстрение времени будет максимально при свободном движении. Вот такой общий случай движения мы и рассмотрим, а начнем мы с классического ПНД2 в этой задаче. Пусть в первом случае (кривая 1 на рис. 3) у нас будет свободное движение в поле тяготения Земли, т.е. по эллипсу, когда точка приземления В находится немного дальше точки расположенной на другой стороне Земли относительно точки старта А, т.е. за кинетическим фокусом, а во втором случае (кривая 2) будет движение, когда снаряд летит в ту же конечную точку по дуге окружности с другой стороны Земли и получается, что он немного не долетает до точки расположенной на другой стороне Земли относительно точки старта. Данная задача, как и многие другие решалась мною численными методами с использованием программы Hrono1R (скачать можно здесь http://modsys.narod.ru ), по этому я приведу только получившиеся численные значения действия и ускорения времени и дам начальные данные для тех, кто надумает сам поработать с программой. Сейчас я выложил уже 2-ю версию программы Hrono, с которой гораздо удобнее работать, но релятивистский расчет я из нее убрал. Если Вы после загрузки программы нажмете на ней кнопку «задача Фейнмана», то у Вас загрузятся все данные необходимые для расчета движения по 1-у пути, а для других путей (это 2, 3 и 4 пути) я приведу дополнительные исходные данные в таблице 3.   

 

 

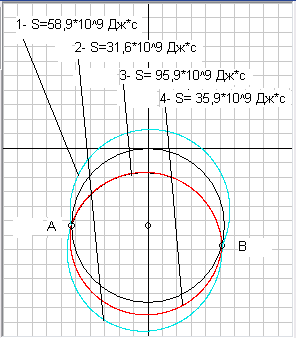
Рис.3. Задача Фейнмана с полетом ракеты в течение часа в поле тяготения Земли.

 

 

Как видим, задача сразу усложняется тем, что у нас оказывается только при движение в одной плоскости из точки А в точку В уже возможно два свободных (прямых, истинных) пути, а, если рассмотреть движение и по оси Z, то наверняка отыщется еще как минимум пара свободных путей, где время движения из точки А в точку В будет 1 час. Возникает вопрос. А какой же из этих путей свободный. Первый или второй. Как ни странно оба, т.к. при движение по этим путям у нас на снаряд не действуют никакие посторонние внешние силы и нет никаких уравнений связей, в которых обязательно появятся силы реакций. Вот только 1-ый путь залетел за кинетический фокус и, следовательно, на нем ПНД уже не работает, чего и следовало ожидать, т.к. еще Эйлер писал, что на другой стороне шара ПНД не работает. Но ни Ландау в своей механике, ни Фейнман в своих лекциях и книге об интегралах по путям, об этом ничего не пишут и у них ПНД применяется как глобальный, а не локальный принцип. В таком случае для опровержения их высказываний мы вправе выбрать любой из этих путей как свободный и сравнить его с несвободным путем. Здесь правда у некоторых читателей может появиться надежда, на то, что на 2-ом пути у нас действие S будет минимальным, а на первом пути максимальным, и тогда ПНД будет выполняться как ПЭД. Но данные таблицы 3 отвергают эту версию, т.к. на 3-ем пути действие оказывается больше, чем на 1-ом. Здесь, надо заметить, что, исходя из возможностей программы Hrono, 3-ий путь в данном примере является чисто теоретическим, т.к. через тело Земли (черный круг) мы пролететь не можем, но если мы допустим, что это заряженная масса движется в поле заряда другой массы, которая отражена точкой в центре Земли, то все выкладки останутся те же. Можно было бы взять и траекторию для 3-го пути не в виде дуги, чтобы он оказался выше 1-го пути и тогда действие тоже будет больше чем на 1-ом пути, но в программе Hrono такой возможности нет.

 

 

Таким образом, так как и 1-ый и 2-ой путь являются прямыми, я могу взять любой из них и сравнить его с окольными путями. Как видим, при сравнение 1-го пути с 4-м путем ПНД не срабатывает и, следовательно, не является глобальным принципом, т.е. применим только на маленьком участке этого пути или до кинетического фокуса, который надо искать индивидуально для каждого случая движения. То же самое мы будем наблюдать, если сравним пути 1 и 4 в релятивистской форме, т.к. замедление времени в ОТО эквивалентно действию в классической механике. Чем больше скорость, тем больше кинетическая энергия и действие, и, точно также, при этом происходит замедление хода часов, а чем больше высота полета, тем больше потенциальная энергия и значит меньше действие и, точно также, с ростом высоты происходит убыстрение хода часов. Так вот на пути 1 у меня получилось ускорение времени dt1= 3,32-9,92= - 6,60 *10^-7 с, а на пути 4  ускорение времени dt4=2,45-6,46= - 4,01 *10^-7 с, т.е. больше чем на прямом пути, а замедление времени меньше. Здесь первая цифра убыстрение хода часов при уменьшение гравитации на высоте H, а вторая цифра это замедление времени от увеличения скорости V. При этом потенциальная энергия рассчитывалась от нулевого уровня, за который принята поверхность Земли.

 

Таблица 3

№	траектория	VX (м/с)	VY (м/с)	t (с)	S*10^9 (Дж*с)	dt*10^-7(с)	Х4 (км)
1	прямой путь	-1380,0	8000,0	3600	58,9	-6,60	-
2	прямой путь	-2447,6	-7740,57	3600	31,6	-3,61	-
3	дуга окружн.	542,13	1617,61	3600	95,9	-10,68	-280
4	дуга окружн.	-1160,5	-6565,6	3600	35,9	-4,01	-150

 

 

 

Таким образом, мы видим, что никаких особых свойств ПНД в релятивистской формулировке не имеет и, следовательно, ему присущи те же недостатки, что и в классической формулировке. А именно – этот принцип имеет локальное значение, т.е. является частным, и применим только для идеальных систем, т.е. когда отсутствует диссипация энергии, а т.к. в реальных процессах диссипация присутствует всегда, то значит практически не применим никогда. Естественно, и все уравнения ОТО полученные из этого принципа не применимы к реальным процессам. А вице-президент АН СССР, ректор МГУ, академик А.Логунов высказался по этому поводу так [42] «тензор энергии-импульса в теории Эйнштейна имеет такое же отношение к физике, как прошлогодний снег к загадке Тунгусского метеорита». При этом, точно так же, как и классический ПНД не может однозначно определить форму траектории, как мы это показали выше, то и релятивистский ПНД не может выполнить этой единственной своей функции, т.е. получить однозначные уравнения движения. К тому же в ОТО появляются какие то проблемы с концами интегрирования и Ландау [4] на стр. 47, когда определяет вариацию действия, почему-то считает конечную точку переменной, а не фиксированной, а тогда появляется некоторая неопределенность в уравнениях полученных из ПНД. Однако, все это не умоляет огромной ценности ОТО и СТО, полученных из этого принципа, для математиков, где они на этой геометрической задаче могут оттачивать свои математические способности.

 

 

А теперь давайте рассмотрим второе событие в физике, которое тоже связано с ПНД, а именно интегралы по путям, которые как считается коренным образом изменили квантовую механику. Ведь как пишет [36]

«в квантовой теории, как она оформилась в результате работ Н.Бора, В.Гейзенберга, В.Паули, Э.Ферми, П.Дирака и др., существовала “проклятая” проблема расходимостей. Попытка решения ее, осуществленная Р.Фейнманом, привела к новому варианту теории и новому методу — методу континуальных интегралов [3]. Фейнмановская трактовка квантовой механики по существу сориентирована на сохранение преемственности с вероятностной копенгагенской интерпретацией квантовой механики и с классической механикой (посредством хорошо известного т. н. предельного перехода). Причем, в центре внимания находится связь квантовой механики с аналитической механикой с помощью квантовомеханической трактовки Лагранжевой и гамильтоновой функции действия.»

 

 

Чтобы вкратце понять о чем идет речь в интегралах по путям Фейнмана, посмотрим как Википедия трактует интегралы Фейнмана, рассматривая принцип наименьшего действия

http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%BD%D0%B0%D0%B8%D0%BC%D0%B5%D0%BD%D1%8C%D1%88%D0%B5%D0%B3%D0%BE_%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D1%8F

«В квантовой механике, в соответствии с копенгагенской интерпретацией, не требуется знать, каким конкретно образом движется частица. Более того, в формулировке Фейнмана утверждается, что:

частица движется из начального состояния в конечное сразу по всем мыслимым траекториям (которых, очевидно, бесконечное число). Амплитуда вероятности перехода из одного заданного состояния в другое является суммой амплитуд по всем этим траекториям и записывается в виде функционального интеграла

 

ψ = ∫[Dx] e^( i S[x] / h )

 

Здесь  ∫[Dx]  — это условная запись бесконечнократного функционального интегрирования по всем траекториям x(t), а h — постоянная Планка. Подчеркнём, что в принципе действие в экспоненте появляется (или может появляться) само, при изучении оператора эволюции в квантовой механике, однако для систем, имеющих точный классический (неквантовый) аналог, оно в точности равно обычному классическому действию.

Математический анализ этого выражения в классическом пределе — при достаточно больших S/h, то есть при очень быстрых осцилляциях мнимой экспоненты — показывает, что подавляющее большинство всевозможных траекторий в этом интеграле взаимосокращаются при этом в пределе (формально при S/h → ∞). Для почти любого пути найдется такой путь, на котором набег фазы будет в точности противоположным, и они в сумме дадут нулевой вклад. Не сокращаются лишь те траектории, для которых действие близко к экстремальному значению (для большинства систем — минимуму). Это — чисто математический факт из теории функций комплексного переменного; на нём, например, основан метод стационарной фазы.

В результате частица в полном согласии с законами квантовой механики движется одновременно по всем траекториям, но в обычных условиях в наблюдаемые значения дают вклад только траектории, близкие к стационарным (то есть классическим). Поскольку квантовая механика переходит в классическую в пределе больших энергий, то можно считать, что это — квантовомеханический вывод классического принципа стационарности действия.»

 

 

А вот короткая цитата из уже цитировавшейся мною лекции [29]

«В квантовой механике, в отличие от механики классической, для описания движения, вместо траектории r(t), используется так называемая амплитуда вероятности для частицы, находящейся в исходный момент времени t_a в точке пространства "a", попасть в момент времени t_b в другую точку пространства — "b". Если обозначить эту амплитуду вероятности через C(a→ b), то для нее справедлива следующая замечательная формула

C(a→ b)=SUM exp(i*Sab/h). Суммирование в этой формуле ведется по всем путям r(t), ведущим из точки "a" в точку "b". А в показателе экспоненты стоит уже знакомое нам действие S_ab (деленное на постоянную Планка ħ), вычисленное для каждого из таких путей. Не правда ли, потрясающе красивая формула? В ней в таком компактном виде заключено одно из величайших творений человеческого гения — квантовая механика. Видно совсем не случайно размерность действия совпала с размерностью постоянной Планка!».

 

 

У человека, прочитавшего это, может сложиться впечатление, что Фейнман создал какую то новую квантовую механику, которая естественным образом перетекает в классическую, также как и релятивистская механика, и задал условия, при которых это происходит, т.е. чтобы действие было сопоставимо с постоянной Планка. Ничего подобного. Квантовая механика с интегралами по путям Фейнмана ничем не отличается от квантовой механики с волновой функцией и Фейнман это неоднократно подчеркивает. Так из-за чего же весь сыр бор. Оказывается только из-за того, что, если начинать изучение не с волновой функции, а с интегралов по путям, то у студента не будет таких сильных нервных припадков. Фейнман так и пишет [26]

«Выяснилось, что для решения более общих задач квантовой механики операторный метод оказывается и глубже, и намного мощнее. Тем ни менее интеграл по траекториям обеспечивает наглядность восприятия квантовомеханических ситуаций, что чрезвычайно ценно при выработке интуитивного понимания квантовых законов.»

 

 

А теперь давайте посмотрим, какое у нас будет интуитивное понимание квантовых законов после того, как мы прочитаем комментарий Фейнмана к его интегралам по путям из его лекций [27]

«...как все-таки частица находит правильный путь? ...Уж не "обнюхивает" ли она соседние пути, прикидывая, к чему они приведут – к большему или меньшему действию? ...Правда ли, что частица не просто "идет верным путем", а пересматривает все другие мыслимые траектории? ...Самое чудесное во всем этом – то, что все действительно обстоит так. Именно это утверждают законы квантовой механики. Так что наш принцип наименьшего действия сформулирован не полностью. Он состоит не в том, что частица избирает путь наименьшего действия, а в том, что она "чует" все соседние пути и выбирает тот, вдоль которого действие минимально, и способ этого выбора сходен с тем, каким свет отбирает кратчайшее время».

А вот в этой статье [32] этот процесс описан еще более захватывающе, но я приведу только маленькую цитату

«Аналогия с пчелами также объясняет, почему в фейнмановской формулировке квантовой механики используются все возможные пути для вычисления амплитуды вероятности любого квантового перехода. На языке пчел, разведчицы исследуют все лужайки, но окончательное коллективное решение состоит только в одной лужайке».

 

 

И после таких комментариев, как пел Высоцкий «остается только материться», т.к. если на приеме у психиатра рассказать, все, что творится в этой шизофренической механике хоть в старой интерпретации, хоть в интерпретации Фейнмана, то я уверен, что диагноз все равно будет предопределен. Но здесь мы опять видим, что математико-физикам по большому счету плевать на физику, т.к. для них самое главное это математика и если это согласуется с их математическими теоремами, то это реально существует и в Природе. Есть, например, у них  мнимые числа, то значит они есть и в Природе, есть у них амплитуда вероятности, то значит она есть и в Природе, т.е. у них нет никаких философских принципов, а только логика математической целесообразности. А вот, например, Пифагор, имел свои философские принципы и верил в рациональное устройство мироздания и возможность описания этого устройства с помощью чисел и их отношений, по этому, когда выяснил, что число π не является простой дробью, а в Природе должны быть только простые дроби, запретил своим ученикам говорить об этом кому-либо, а то, по его мнению, мир разрушится.

 

 

Но давайте немного успокоимся и попытаемся разобраться с интегралами по путям с чисто математической и физической точек зрения. И начнем с того, что Фейнманом не дано строгого определения интегралу по траекториям. Об этом, например, пишет в своем предисловие редактор перевода книги Фейнмана «Квантовая механика и интегралы по траекториям» [26].

«В книге Фейнмана и Хибса не дано строгого определения интеграла по траекториям; он вводится чисто интуитивно как предел соответствующего многократного интеграла (заметим, что введение комплексной единицы существенно усложняет строгое обоснование такого предельного перехода). Впрочем, для физика это в большинстве случаев не очень важно; ему нужна лишь уверенность, что строгое доказательство может быть получено.»

А вот здесь автор перевода перепутал принципы математиков с принципами физиков, а заодно забыл, что Фейнман математико-физик, т.е. математик перебежавший в физику. Но со строгой  формулировкой то действительно получилось не красиво и Фейнман неоднократно сталкивается с этой проблемой.

 

«стр. 46. Однако точно так же, как и в случае интеграла Римана, невозможно достичь предела этого процесса, так как такой предел не существует. Мы снова должны ввести некоторый нормирующий множитель, который, как и следует ожидать, будет зависеть от ε.

К сожалению, определение такого нормирующего множителя оказывается весьма трудной задачей, и неизвестно, как это делать в общем случае.»

«стр. 47. Имеется много способов выбрать некоторое подмножество из всех траекторий, проходящих через точки a и b. Применявшийся нами способ, возможно, не является наилучшим с точки зрения математики. Предположим, например, что лагранжиан зависит от ускорения в точках ...»

«стр. 48. Необходимость уточнить способ интегрирования вовсе не дискредитирует саму идею. Просто речь идет о том, что возможные неудобства, связанные с нашим определением суммы по траекториям [см. выражение (2.22)], в конечном счете могут потребовать формулировки новых определений.»

 

 

Таким образом, Фейнман сам подтверждает, что пока интегрирование по путям является просто идеей или в лучшем случае гипотезой, которую еще надо долго доводить до теории. Но трудности у него возникают не только с самим суммированием по путям, но и буквально с каждой величиной входящей в его формулу.

«стр. 37. Отыскание строгого метода вычисления амплитуд вероятностей процессов с участием таких (представляющихся сейчас более сложными) частиц, как нуклоны и мезоны, является задачей будущего. ... В то же время детали взаимодействий все еще ускользают от нас. Это наводит на мысль, что амплитуды вероятности будут существовать и в будущей теории, однако метод их вычисления может оказаться для нас весьма необычным.»

«стр. 52. В релятивистской теории электрона мы не сможем выразить амплитуду вероятности, соответствующую некоторой траектории, в виде  e^( i S / h ) или каким-либо другим простым способом.»

 

Но, оставим все эти математические проблемы Фейнману и займемся рассмотрением того, в каком виде он использовал ПНД в своей идее интегралов по путям. Сразу скажу, что о принципе стационарного действия (ПСД) Фейнман ни разу даже не упомянул, а по тексту видно, что он путает ПНД и ПСД. Его формулировку ПНД в этой работе именно как принципа наименьшего действия я уже приводил выше, где Фейнман пишет, что при этом фактически используют только свойство экстремальности действия. И Фейнман находит вид экстремальной траектории из условия, что первая вариация равна нулю, т.е. мы видим, что совершает ту же самую математическую ошибку, что и Ландау, т.к. это является только необходимым, но не достаточным условием экстремума. В общем, прекрасные математики нас что-то огорчают своими познаниями в вариационном исчислении, по этому, я даже затрудняюсь стоит ли дальше цитировать Фейнмана, т.к. нет никакой уверенности, что его рассуждения вытекают не из этой ошибки. Да действительно дальше у него уже в квантовой механике кругом идет речь именно о минимуме действия или об его экстремальности, но это нисколько не говорит о том, что это должно быть именно так. Однако одна его фраза заставляет предположить, что ему для его интеграла по траекториям все-таки нужен именно экстремум функционала

«В классической механике важен вид интеграла S = ∫ L dt, а не его экстремальное значение Sкл. Это обусловлено тем, что для определения траектории, соответствующей наименьшей величине действия, необходимо знать действие S для всего семейства близколежащих траекторий.

В квантовой механике важны как сам вид интеграла S, так и его значение в точке экстремума.»

 

 

А логические рассуждения приводят меня к выводу, что ему для оправдания своей великой идеи интегралов по путям именно и нужен минимум или экстремум, т.е. какой то отличительный признак, который бы отличал все остальные пути от истинного. Ну, какой ему прок от стационарности действия, если при этом на истинном пути действие будет иметь любое произвольное значение. Ведь ему надо доказать, что в классическом пределе будет именно истинный путь, а не какой то произвольный. Ведь точно также можно ткнуть пальцем в небо и обязательно попадешь в какую ни будь точку. А ему надо доказать, что он попал именно в ту точку, куда и надо было попасть. Таким образом, можно сделать вывод о том, что для доказательства своей идеи Фейнман использовал именно ПНД, а не ПСД, но при этом он не указал условий, когда его идея будет подтверждаться, т.к. ПНД справедлив только в частном случае движения частицы до кинетического фокуса. Следовательно, ему для уточнения своей идеи надо еще определить правила для определения времени до которого его идея может быть использована, но этот вопрос у Фейнмана практически не рассмотрен. Он вроде бы заикнулся на стр. 43 об этом, но все рассуждения свел к классической механике, а там мы уже знаем, что все упирается в кинетические фокусы. Но Фейнман то о кинетических фокусах ничего не знает, по этому никаких проблем с конечной точкой у него не возникает. Тем более что в квантовой механике вообще стараются не говорить о времени.

 

 

Таким образом, т.к. ПНД не работает на другой стороне шара, то Фейнман не может суммировать все пути в своих интегралах по путям. В лучшем случае он может взять половину путей, т.е. с одной стороны шара и до кинетического фокуса. И все это при условии движения в монополе, а в мультиполях определение того, что можно суммировать в его интегралах по путям, еще более усложнится. Но в любом случае делать так как он, т.е. суммировать амплитуду вероятности по всем путям, когда она определяется с использованием ПНД, категорически нельзя. Следует также отметить, что само условие, когда движение из квантово-механического переходит в классическое у Фейнмана очень расплывчатое. Он пишет

«Однако классическое приближение соответствует случаю, в котором размеры, массы, интервалы времени и другие параметры системы настолько велики, что действие S во много раз превосходит постоянную ħ=1,05*10^-27 эрг*сек.»

«Однако на атомном уровне действие S может быть сравнимо с величиной ħ, и тогда в выражение (2.14) должны учитываться все траектории.»

Если мы вычислим действие для электрона, летящего по первой Боровской орбите, за пол оборота, то мы уже получим действие 4,95*10^34 Дж*с, что почти в пять раз больше постоянной Планка (ħ=1,05*10^-34 Дж*с). А, если рассмотрим движение частиц в ускорителях, где скорости на два порядка больше, чем на первой Боровской орбите (2180 км/с), то мы получим действие на несколько порядков превышающее постоянную Планка и, таким образом, по Фейнману получается, что в этом случае мы должны применять к этим частицам уже законы классической механики.

 

 

И так мы видим, что (даже без последнего замечания) единственный пример, где ПНД используется якобы как ПСД, оказался липовым. Но и это еще не все. Оказывается, что именно ПНД к идее Фейнмана не имеет никакого отношения, т.к. его идею интегралов по путям, т.е. переход от квантовых законов к классическим можно было бы реализовать и на любом другом вариационном принципе, коих в классической механике предостаточно. Возьмем, например, принцип наименьшего принуждения Гаусса, формулировку которого я лучше приведу из современных справочников, а то в оригинале многие могут что-то не понять. Вот как это звучит на http://allphysics.ru/phys/gaussa-printsip

«Физ. величина, наз. «принуждением», вводится след. образом. Свободная матер. точка с массой m при действии на неё заданной силы F будет иметь ускорение F/m; если же на точку наложены связи, то её ускорение при действии той же силы станет равным какой-то др. величине w. Тогда отклонение точки от свободного движения, вызванное действием связи, будет зависеть от разности этих ускорений, т. е. от F/m-w. Величину Z, пропорц. квадрату этой разности, и наз. «принуждением». Для одной точки

Z=¹/₂m(F/m-w)².

а для механич. системы Z равняется сумме таких величин.»

 

 

Ну и, чтобы стало еще более понятно о чем идет речь, уместно будет привести несколько выдержек и из статьи Маркеева [19]

«Принципу наименьшего принуждения можно дать теперь такую формулировку: действительное движение среди кинематически возможных выделяется тем, что для него работа реакций связей на путях отклонения этого движения от свободного движения в каждый данный момент есть минимум.»

«Принцип Гаусса может быть выражен теперь в следующей форме: действительное движение есть одно из движений, совместимых со связями, для которого в каждый момент времени сумма отношений квадратов реакций в каждой отдельной точке к соответствующей массе есть минимум.»

 

 

А, чтобы уж совсем стало понятно, я приведу свою формулировку этого принципа для одного тела «на истинном пути движения тела квадрат реакции связи деленный на две массы тела в каждый момент времени является минимумом, а, если у нас вообще отсутствуют связи, т.е. мы рассматриваем свободное движение, то принуждение будет равно нулю.»

Но если дифференциальный принцип наименьшего принуждения выполняется для каждого момента времени, то он будет выполняться и на интервале от t1 до произвольного t2, т.е. будет являться глобальным интегральным принципом в отличие от локального ПНД, который работает только до кинетического фокуса, и по этому более естественно было бы доказать Фейнману переход от квантового состояния к классическому именно на этом глобальном принципе. Но, я так догадываюсь, что он, также как и Ландау, и не слышал об этом вариационном принципе, т.к. на слуху был только ПНД. К тому же и размерность постоянной Планка позволяла получить безразмерную величину в показателе экспоненты только при использование ПНД. Но ведь математикам не привыкать изобретать различные нормировочные множители. Так что и здесь ввели бы какую ни будь буковку. Для них же вся физика это только буковки.

 

 

А можно предложить и совершенно новый интегральный принцип, который я только что сочинил специально для интегралов по путям Фейнмана немного взяв из принципа Гаусса, немного из принципа Журдена и немного добавив от себя. Звучит ПНД3 так

«при свободном движение тела из точки 1 в точку 2 между моментами времени t1 и t2 действие будет равно нулю, а на всех окольных путях, т.е. при движение по каким то направляющим (или при воздействие дополнительных внешних сил), действие будет равно интегралу от произведения реакции связи (или внешних сил) на элемент пути и элемент времени, т.е. S= ∫ R*ds*dt.»

Если элемент пути заменить на V*dt и затем взять интеграл по t между промежутками времени t1 и t2, то мы получим размерность действия, т.е. Дж*с, и Фейнман может теперь со спокойной совестью вычислять это действие для всех окольных путей, чтобы найти для них амплитуду вероятности, т.к. здесь, точно так же, как и в ПНД1 и ПНД2, чем дальше окольный путь отстоит от прямого, тем будет больше действие. А в программе Hrono2 я даже дополнил возможность вычисления действия на различных путях по ПНД1 и ПНД2 еще возможностью вычислять принуждение по принципу Гаусса и действие по своему принципу ПНД3. И на рис. 4 приведен пример движения тела массой 1 кг по прямому пути и нескольким окольным из точки А (-40;0) в точку В (40;20,7), а в таблице 4 даны для сравнения величины действия, получающиеся по ПНД2 (T-U), ПНД3 (R*S) и величина принуждения в интегральном принципе Гаусса (R^2), а также дано время движения в секундах и начальная скорость в м/с.

 

 

 

 

 

Рис.4 Движение тела из точки А в точку В в плоском поле постоянной напряженности (локальное поле тяготения Земли при g=9,8 м/с/с) по прямому (свободному) пути 4 и по различным окольным путям.

 

 

Табл. 4

траектория	t	V0	T- U	R*S	R^2
1 - дуга окружности X40=1м	3,477	43,96	986,3	2,97	1093,5
2 - дуга окружности X40=5м	3,478	37,76	592,7	1,24	292,1
3 - дуга окружности X40=12,5м	3,478	32,77	463,9	0,23	22,2
4 – свободное движение	3,479	32,53	460,1	0,0	0,0
5 - дуга окружности X40=15м	3,478	31,98	464,3	0,21	13,2
6 - прямая	3,478	28,03	618,5	0,78	156,6
7 - дуга окружности X40= -10м	3,477	26,82	1235,0	1,97	783,8

 

 

Надеюсь, что теперь то уже всем понятно, что ПНД2 не имеет к интегралам по пути Фейнмана никакого непосредственного отношения, а сами эти интегралы, естественно, являются только неудачной гипотезой Фейнмана. Но и это еще не все. Сейчас я докажу, что Фейнман даже не имел права использовать ПНД2 для своих интегралов. Ведь у него получается, что одна и та же частица одновременно летит и по прямому (свободному) пути и по всем окольным, т.е. по каким то направляющим и одновременно долетает по всем этим путям из точки 1 в точку 2. Не будем останавливаться на том, как одна и та же частица летит сразу по бесчисленному множеству путей, т.к. нам этого все равно не понять. Давайте посмотрим, а та ли это самая частица летит по всем этим путям. Ведь для того, чтобы частице прилететь за одно и тоже время по разным путям в конечную точку, ей надо в начальный момент времени иметь разные начальные скорости. А т.к. сторонники квантовой механики не знают, что такое скорости, тогда скажем, что ей надо иметь различные импульсы. Их то они уважают. Но тогда получается, что по разным путям летят совершенно разные частицы с разными начальными импульсами, а для интегралов Фейнмана это совершенно не подходит, т.к. у него должна лететь одна и та же частица. Таким образом, лопнул мыльный пузырь последней надежду сторонников применения ПНД в механике, где, как они утверждают, он соблюдается как ПСД, т.к. теперь им абсолютно не на что сослаться, где бы в механике применялся ПНД. А раз он нигде не применяется то и делать ему в механике нечего. Разве что оставить его в курсе «Истории механики» и поместить эту кафедру, как и предсказывал Лагранж, рядом с кафедрой арабского языка.

 

 

А, что касается всех этих вариационных принципов в механике, то Гаусс по этому поводу отлично написал [17]

«Как известно, принцип виртуальных скоростей превращает любую проблему статики в вопрос чистой математики, а с помощью принципа Д’Аламбера динамика в свою очередь сводится к статике. Отсюда следует, что ни один основной принцип равновесия или движения не может существенно отличаться от двух упомянутых нами выше принципов и что каков бы ни был этот принцип, его всегда можно рассматривать как более или менее непосредственный вывод из них.

Это не значит, что всякая новая теорема не заслуживает по этому никакого внимания. Наоборот,  всегда интересно и поучительно исследовать законы природы с новой точки зрения, придем ли мы при этом к более простому трактованию того или иного частного вопроса или достигнем лишь большей точности формулировок.»

 

 

Таким образом, все эти вариационные принципы и дифференциальные и интегральные не могут дать механике ничего нового и изобретение новых принципов и их использование является только развлечением для математиков, которым нечем заняться в математике. Кстати, у Гаусса это единственная работа, посвященная механике, которая к тому же перекликается с его методом наименьших квадратов, т.к. ему в отличие от других бездарей математиков было чем заняться в математике. Да и сам его принцип наименьшего принуждения вполне приличный принцип (в отличие от ПНД) и даже позволяет очень остроумно решить несколько простейших механических задачек. А вот этому ПНД, как будет еще показано и ниже, уж точно нет никакого места в механике, и использовать его можно только в математике. А, чтобы уж окончательно разобраться с ПНД1 и ПНД2 давайте рассмотрим три принципиальных отличия, которые есть в этих принципах, и о которых говорят очень редко (кроме 2-го), т.к. при наличие этих отличий эти два принципа даже не могут существовать одновременно. Вот эти отличия

1-м отличием является то, что разные принципы получены из разных правил вариационного исчисления.

2-м отличием является то, что ПНД1 применим в статических полях, а ПНД2 и в динамических, т.е. когда напряженность поля может изменяться со временем.

3-м отличием является то, что в ПНД1 на свободном пути и на окольных путях рассматривается движение одного и того же тела, а в ПНД2 движения разных тел.

 

 

1-е отличие. Дело в том, что одни математики считают, что время является не варьируемой величиной, а другие считают, что и оно должно варьироваться, как и все остальные переменные. В частности и Эйлера и Лагранжа считают обоих создателями вариационного исчисления. Естественно, заложил его основы для решения геометрических задач Эйлер, который затем применил это исчисление и к решению задач механики. Но, наверное, не меньший вклад в создание вариационного исчисления внес и Лагранж. Вот только Эйлер считал, что время является не варьируемой переменной, а Лагранж считал, что и время варьируется. А при таком подходе можно из одних и тех же аксиом механики получить совершенно разные ПНД или в формулировке Лагранжа или в формулировке Гамильтона. Таким образом, до тех пор, пока математики не определятся с правилами варьирования переменных, бессмысленно говорить вообще о каких либо ПНД. Ведь это равнозначно тому, что в арифметике одни авторы будут использовать таблицу умножения где дважды два будет четыре, а другие авторы будут использовать таблицу умножения где дважды два будет пять. Кстати, насчет арифметики. Как остроумно заметил Эддингтон, сам ПНД можно сравнить с утверждением, что «если бы законы арифметики перестали быть верными, то 2+2 было бы больше или равно (но наверное не меньше) четырем».

 

 

А, т.к. я не являюсь специалистом по вариационному исчислению, я предоставлю право объяснить в чем состоит разница в разных способах варьирования времени Полаку, которое он дает в своей редакционной статье к сборнику [10]. Тем более что в этих выкладках я не понял почему у Гёльдера энергия системы равняется T-U, т.к. по идее должно быть T+U.

«Вопрос о смысле вариации в принципах Гамильтона и наименьшего действия рассмотрел в 1896 г. Гёльдер. Для того чтобы составить отчётливое представление о смысле вариации, необходимо каждое положение точки при варьированном движении отнести и какому-либо положению точки в первоначальном положении. Без установления такого соответствия нельзя написать

δ ∫ T*dt = ∫ δ(T*dt).                             (53)

Установить такое соответствие можно произвольно, так как оно лишено физического смысла : вариация движения есть только математическое вспомогательное построение. Вариация времени будет разностью между моментами прохождения через соответствующие положения.

Для того чтобы выполнить вариацию движения, сообщим сначала каждой точке первоначальной траектории некоторое смещение, так что возникает новая траектория с точками, соответствующими исходной траектории ; затем определим скорость каждой точки новой траектории, причем она может быть произвольной, но возможно мало отличающейся от скорости в соответствующей точке исходной траектории.

Эту скорость можно определить двумя способами : 1) соответствующие точки обеих траекторий проходятся одновременно, 2) полная энергия для соответствующих точек одна и та же.

Так как полная энергия есть T-U, а первоначальное движение задано, то для каждого положения варьированного движения сначала известна лишь потенциальная энергия, и затем в силу E=T-U из условия варьирования получается значение кинетической энергии, а следовательно, и скорости.

Легко видеть, что при втором способе варьирования время варьируется, а при первом – нет.

 

Вывод интегрального принципа для общего случая варьирования приводит Гельдера при допущении, что вариация движения выполнена так, что δxi, δyi, δzi есть виртуальные перемещения системы, к выражению

∫ {2 T d δt + (δT + δ’U)dt} =0          (53’)

где  δ’U = Σ (X δxi + Y δyi + Z δzi) - работа, которую совершили бы действующие силы на одном из этих воображаемых перемещений.

Воспользуемся теперь двумя введенными способами вариации. При изохронной вариации δt = 0 и из формулы (53’) получим :

∫ (δT + δ’U) dt = 0,                      (54)

т.е. принцип Гамильтона. При изоэнергетической - δT = δ’U  и из (53)

∫ δ (T dt) =δ ∫ (T dt) = 0,              (55)           

т.е. принцип наименьшего действия.»

 

 

А, как Вы, наверное, догадались, из разных «таблиц умножения» вытекают и разные требования при применение ПНД1 и ПНД2 для нахождения истинных путей. Для ПНД1 при сравнение истинного пути с окольным путем начальные скорости в двух этих движениях по модулю должны быть равны, а время движения из точки А в точку В может быть разным, а в ПНД2 начальные скорости в двух сравниваемых движениях могут быть не равны, но время движения из точки А в точку В должно быть одинаковым. Я не математик и, наверное, не вправе указывать им допустимо ли это в математике, но все же, как механик, я считаю факт того, что за 300 лет применения вариационного исчисления математики так и не договорились между собою о том какие переменные у них варьируются, а какие нет, является сущим безобразием. Причем, когда нам дают две совершенно разные формулировки вроде бы одного и того же принципа, нам никто не объясняет, что вообще то формулировка должна быть одна, но какая из них правильная нам скажут, когда математики договорятся о том какие переменные варьируются в вариационном исчислении. А пока математики додумались только до того, что одну таблицу умножения назвали изохронным варьированием (не полная вариация), а другую не изохронным (изоэнергетическим или полной вариацией). Но, как механик, я могу сказать уже сейчас, что с точки зрения механики правильным является только ПНД1. А вот Эйнштейна все эти тонкости не интересуют и он выводит свои уравнения ОТО из ПНД2, где время не варьируется, потому что является независимой переменной, но у него то в ОТО оно является уже зависимой переменной также как и пространственные координаты и по этому ему надо было использовать ПНД1. Но Эйнштейн здесь не одинок и современные авторы, как отмечается в статье [41], тоже выводят уравнения ОТО и СТО из ПНД2, но одни ухитряются выводить эти уравнения варьируя псевдовремя, а другие не варьируя. Естественно, у них при этом должны получатся разные уравнения, но этот момент почему-то никого не беспокоит.

 

 

2-е отличие. Напоминаю, что ПНД1 применим в статических полях, а ПНД2 и в динамических, т.е. когда напряженность поля может изменяться со временем. Но прежде чем говорить о применение ПНД2 в динамических полях давайте выясним что же это такое. Из функционала Гамильтона-Остроградского следует, что это поле в котором потенциальная энергия системы может зависеть не только от координат тела, но и от времени, а т.к. потенциальная энергия по определению является только функцией координат, то такое возможно только при изменении координат и источника, создающего поле потенциальных сил. Таким образом, получается, что в этом случае мы должны задать скорость перемещению этому источнику. Для полей существующих в Природе мы этого сделать не можем, но для некоторых полей мы можем это сделать искусственно. Глупо конечно говорить о том, что мы можем изменять гравитационное поле в функции времени, т.к. для этого нам бы пришлось таскать на веревочках с заданной скоростью гравитационные массы сопоставимые с массами планет. А вот справится с электроном нам вполне по силам и мы можем заставить его лететь или в переменном электрическом поле или в переменном электромагнитном поле. Хотя и для гравитационных полей мы тоже можем кое-что придумать остроумное. Например, мы можем рассматривать движение Луны не при движение ее вместе с Землей вокруг Солнца, а рассмотреть движение Луны только вокруг Земли и при этом поле тяготения создаваемое Солнцем задать как изменяющееся в функции времени, т.к. нам известен закон по которому Земля вместе с Луной движутся вокруг Солнца.

 

 

Вообще то именно для этих целей Гамильтон и изобретал свою характеристическую функцию, а Лагранж для этих целей использовал пертурбационную функцию, но сейчас ни то ни другое для описания движений планет не используется. НАСА уже 50 лет как использует компьютеры для решения системы дифференциальных уравнений, описывающих движение планет, численными методами, а я при создание своей теории планет вообще применил чисто статистические методы обработки данных наблюдений за планетами, хотя у меня, как и у НАСА тоже есть своя математическая модель Солнечной системы. Таким образом, по большому счету, для практических целей необходимость в использование переменных полей в функции времени сохраняется пока еще только в квантовой механике. Вот только при описание движения отдельного электрона в атоме вокруг ядра также как и с Луной не получится и мы не сможем поля создаваемые другими электронами задать в функции времени заранее, т.е. до решения задачи о нахождение траектории движения нашего электрона в функции времени, т.к. их траектории также будут очень зависеть от траектории нашего электрона. При движение Луны ее влиянием на движение Солнца и других планет можно пренебречь, а вот при движение отдельного электрона его влиянием на другие электроны пренебрегать нельзя. Но в этом случае получается система дифференциальных уравнений, которая не решается аналитически (задача трех тел) и по этому математико-физики ее и не решают, а используют в квантовой механике только статистические методы.

 

 

И вот здесь мы с Вами в вопросе полей изменяющихся в функции времени упираемся в вопрос о том, что можно считать системой тел, а что условиями функционирования этой системы.  Ни Гамильтон, который рассматривал движение луча света, ни Остроградский, который рассматривал геометрические фигуры, при получение ПНД2, естественно, ни о каких системах тел писать не могли и в формулировке Гамильтона появилось утверждение о движение системы тел только когда он потом формулировал свой принцип для механики. А вот Лагранж при формулировке ПНД1 в своей Аналитической механике [18] сразу написал, что

«Указанное свойство, найденное Эйлером при движении изолированных тел, которое представлялось присущим только этим телам, я, пользуясь принципом сохранения живых сил, распространил на движения любой системы тел, действующих друг на друга каким угодно образом; отсюда вытекает новый общий принцип, согласно которому сумма произведений масс на интегралы скоростей, умноженных на элементы пройденных путей, является всегда максимумом или минимумом.

Таков тот принцип, которому, хотя и не вполне точно, я даю здесь название принципа наименьшего действия и на который я смотрю не как на метафизический принцип, а как на простой и общий вывод из законов механики.»

 

 

А далее он дает и более развернутую формулировку этого принципа, но взаимодействие между телами системы сводит практически к силам притяжения или отталкивания

«При движение любой системы тел, находящихся под действием взаимных сил притяжения, или сил  направленных к неподвижным центрам и пропорциональных каким-либо функциям расстояний, кривые, описываемые различными телами, а равно их скорости, необходимо таковы, что сумма произведений отдельных масс на интеграл скорости умноженной на элемент кривой, является максимумом или минимумом – при условии, что первые и последние точки каждой кривой рассматриваются как заданные, так что вариации координат, соответствующих этим точкам, равны нулю.»

 

 

Причем, когда он выводит этот принцип из принципа сохранения живых сил S*m*(v^2/2 +П) = H, то он к тому же и особо оговаривает, что связь между телами не зависит от времени. И только уже после вывода из общих уравнений динамики этого принципа он коротко замечает, что

«Впрочем, так как ds=V*dt , то величина S*m* ∫ V*ds , которая представляет собою максимум или минимум, может быть приведена к следующему виду : S*m* ∫ V^2*dt или  ∫ dt*S*m*V^2, где  S*m*V^2 выражает живую силу всей системы в любое мгновение. Таким образом, рассматриваемый принцип сводится, собственно, к тому, что сумма живых сил всех тел от момента, когда они выходят из заданных точек, до того момента, когда они приходят в другие заданные точки, является максимумом или минимумом. Следовательно, его можно было бы с большим основанием назвать принципом наибольшей или наименьшей живой силы...»

В этом замечание он даже не приводит новой формулировки своего принципа, но все авторы почему-то дают его принцип именно в последней формулировке. Причем дают его не для системы тел, а для отдельного тела, но Лагранж считал, что его принцип отличается от принципа Эйлера именно тем, что Эйлер его сформулировал для движения отдельного тела, а он для движения системы тел.

 

 

Здесь, наверное, надо сделать некоторое отступление от темы и дать пояснения по поводу принципа сохранения живых сил. Понятия «работа», «энергия» и самого «закон сохранения энергии» появились в науке уже после смерти Лагранжа, а до этого кинетическая энергия называлась живой силой (правда выражалась формулой m*V^2), а закон сохранения энергии формулировался в виде принципа сохранения живых сил. По этому, формулировку принципа сохранения живых сил в дифференциальной форме я дам из Теоретической механики Леви Чевита 1922 года, который уже был знаком с современными терминами, но при этом и помнил старые [8]

«во время движения материальной системы с какими угодно связями и под действием каких угодно сил приращение, которое получает живая сила системы за какой-нибудь элемент времени, равно полной работе, совершаемой за тот же самый элемент времени всеми силами, действующими на систему.»

 

 

Так в чем же отличие движения отдельного тела от движения системы тел и что такое система. Здесь мне придется дать свое определение системе, которое я формулирую так

«система это ограниченное число элементов объединенных связями так, что они позволяют ей функционировать определенным образом, позволяющим идентифицировать этот набор элементов как вполне определенную систему и при этом система функционирует так, что не оказывает практического влияния на условия в которых она функционирует».

Например, Солнечная система характеризуется конечным набором планет связанных между собою силами тяготения и вся эта система не оказывает никакого практического влияния на окружающие ее галактики и по этому условия функционирования системы не меняются. А можно и отдельно Землю и Луну рассмотреть как систему, которая также практически никакого влияния не оказывает на другие планеты и Солнце, а их воздействие на нашу систему считать условиями функционирования системы, но в данном случае у нас все же будет маленькая погрешность в решении, т.к. хоть и небольшое влияние на движения других планет, но все же Земля имеет. Таким образом, вопрос о минимальном числе элементов входящих в систему решается допустимой погрешностью решения конкретной задачи.

 

 

Вот только, говоря о ПНД, мы почти всегда говорим о свободном движение отдельного тела или в лучшем случае о телах Солнечной системы, но ведь ПНД применим к любым механическим системам. Взять, например, кривошипно-шатунный механизм. Это ведь тоже система. Но я ума не приложу каким образом ПНД может мне помочь при исследование этой системы. Единственное, что приходит на ум так это то, что я могу получить уравнения описывающие движение этого механизма. Вот только тем, кто не пробовал это делать, я настоятельно рекомендую получить уравнения движения идеального кривошипно-шатунного механизма (без сухого трения, без зазоров, все элементы абсолютно жесткие) используя ПНД и для простоты принять, что поршень движется в горизонтальной плоскости. А после того, как Вы затратите несколько недель на это занятие, ответьте на вопрос – а что мне эти уравнению дают. Могу ли я, например, найти усилия, возникающие в шарнирах, или выявить резонансные частоты. Отвечу сразу – ничего этого Вы из полученных Вами уравнений найти не сможете и таким образом полученные таким методом уравнения можете сразу выбросить на помойку. А я вот, например, используя свой метод составления дифференциальных уравнений (модифицированный принцип Даламбера), опишу движение реального кривошипно-шатунного механизма за 5 минут и по полученным уравнениям отвечу на все поставленные мною выше вопросы, для того чтобы грамотно сконструировать данный механизм. Кого заинтересовали тонкости этого вопроса могут ознакомиться с моей программой Krivoship1, в которой движение кривошипно-шатунного механизма описывается дифференциальными уравнениями полученными с использованием лагранжиана и с применением моего метода получения уравнений движения механических систем. Кроме того, в приложении к программе можно посмотреть и вывод уравнений с использованием лагранжиана, а с моим методом получения уравнений движения можно ознакомиться в работах [22, 23].

 

 

А теперь давайте вернемся к вопросу - почему ПНД1 не применим к полям, изменяющимся в функции от времени. Дело в том, что здесь получается различная конфигурация полей в начале пути и в конце, а в таком случае получается, что со временем изменяется потенциальная энергия тела, даже в том случае, если оно стоит на месте. Т.е. формально получается, что нарушается закон сохранения энергии, а в таком случае ПНД1 не может быть применим. Ведь о ПНД1 Лагранж так и писал, что «его можно было бы с большим основанием назвать принципом наибольшей или наименьшей живой силы», т.е. просто признать оригинальной формулировкой закона сохранения энергии на истинном пути. И это прекрасно видно из ПНД1 в той форме, которую ему придал Якоби, исключив из него время, т.к. теперь становится отчетливо видно, что смысл этого принципа состоит в том, что на истинном пути движение должно происходить без отклонений от закона сохранения энергии и это подтверждает и Ландау [3]

«Таким образом, укороченное действие имеет минимум по отношению ко всем траекториям, удовлетворяющим закону сохранения энергии и проходящим через конечную точку в произвольный момент времени.»

 

 

А вот у ПНД2 в динамических полях на истинном пути действие имеет минимальное значение, а закон сохранения энергии для движущегося по этому пути тела не соблюдается и в этом видели исключительность такой величины как действие. Но в данном случае для этого тела или системы тел закон сохранения энергии и не должен соблюдаться. Он должен соблюдаться только для всей системы движущихся тел (включая создающие переменное поле). Но, если в ПНД2 оставить только статические поля, то он вполне может быть заменен ПНД1, который иногда даже называют укороченным ПНД, по этому сторонники ПНД упорно держаться только за формулировку ПНД как ПНД2, которая дает им больший простор для фантазии, да и подынтегральное выражение (лагранжиан) при этом выглядит более загадочно, чем просто кинетическая энергия. Но давайте, наконец-то, посмотрим как ПНД2 работает в динамических полях на конкретном примере и используем для этого программу Hrono2. На рис.5 и 6 Вы видите движение тела заряженного отрицательно (q=0,0005K) из точки А(-40;0) в точку В(34,18;0) в электростатических полях создаваемых двумя телами заряженными положительно (q=0,0005K). При этом на левом рисунке оба положительных заряда остаются неподвижными, а на правом рисунке первый заряд так и остался неподвижным, а правый заряд движется со скоростью VX=VY=3 м/с.

 

 

 

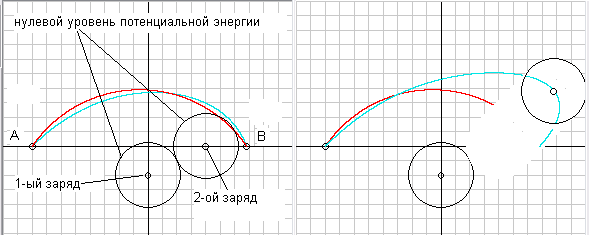
Рис. 5. Движение заряженного тела в полях неподвижных зарядов.

 

Рис. 6. Движение заряженного тела в полях одного неподвижного заряда и одного подвижного.

 

 

На этих двух рисунках я сравниваю два свободных движения (сиреневая кривая) с одним и тем же несвободным, а конкретно по дуге окружности радиусом 45м (красная кривая). Так вот в этих двух схожих примерах у меня получается, что ПНД2 не работает ни в статических полях, ни в динамических. Конкретно у меня в первом примере при свободном движение (VX=VY=10 м/с) действие получилось S= -446,04 Дж*с (1854,20), а при несвободном движении (VX=5,309 м/с, VY=7,727 м/с) действие получилось S= -574,59 Дж*с (1725,65). На обоих путях время движения было 5,715 с, а в скобках указано действие, если потенциальную энергию считать не от задаваемого мною нулевого уровня, а от точки удаленной в бесконечность, как это принято у математико-физиков. А при движение в двух полях я нулевой уровень не просто задаю, а рассчитываю как половину расстояния между двумя телами, создающими эти поля, и в этих примерах у меня нулевой уровень был на радиусе 11,18 м и на рисунках Вы видите эти окружности вокруг зарядов.

 

 

А во втором примере, когда второй заряд двигался, у меня получилось, что при свободном движение тело успело пролететь над этим зарядом, а при движение по дуге пролетело уже под зарядом. При этом при свободном движение (VX=VY=9,1667 м/с) действие получилось S= -426,85 Дж*с (2126,55), а при несвободном движении (VX=5,159 м/с, VY=7,509 м/с) действие получилось S= -1025,54 Дж*с (1527,86). На обоих путях время  движениях было 6,344 с. Да, конечно же, найдется множество других примеров, где ПНД выиграет в динамических полях, но это в любом случае будет не закономерность, а игра в рулетку. Мне могут возразить, что в данном примере конечная точка лежит за кинетическим фокусом и по этому ПНД здесь применять нельзя. Но в таком случае – зачем он вообще нужен этот ПНД, если мне надо найти истинную траекторию движения именно между этими конкретными точками. И таким образом ПНД это просто игрушка, в которую с азартом играли Ландау и Фейнман, и которая не имеет никакого отношения к реальным задачам.

 

 

3-е отличие. Даже, если мы предположим, что обе формулировки ПНД правильные, но для разных условий функционирования системы, которую мы рассматриваем, то все равно в разных формулировках ПНД надо уточнять и условия для вычисления действия на истинном и окольном путях для этой формулировки. Но математико-физики также как и ученые древней Греции считают практические вычисления презренным ремеслом и по этому практически никто из них (кроме Слудского) не соизволил посчитать значения действия при использовании различных формулировок ПНД. А, если бы они это сделали, то, конечно же, сразу бы обратили внимание, что условия для определения действия в ПНД1 и ПНД2 совершенно разные и отразили бы это в своих формулировках ПНД. Ведь в ПНД1 у нас в сравниваемых путях должна быть одна и та же начальная скорость тела по модулю, а в ПНД2 у нас скорости могут быть произвольными, но время движения из точки 1 в точку 2 должно быть одно и тоже. А в последнем случае, как мы уже с вами рассмотрели в интегралах по путям Фейнмана, получается, что мы сравниваем между собою движения совершенно разных тел. По этому, не понятно о каком сравнение здесь вообще может идти речь.

 

 

Да, я понимаю Гамильтона и Остроградского, когда они создавали этот принцип для решения геометрических задач, т.к. не были физиками. Причем, Гамильтон, будучи директором обсерватории больше интересовался оптикой, по этому, и получил свой принцип именно для движения лучей света. Это уже потом он приспособил свой принцип для задач механики и в частности применил характеристическую функцию для описания возмущенного движения планет. А Остроградский вообще решал чисто геометрическую задачу изопериметров, где бестелесные линии можно дергать куда захочешь, и как частный случай этого решения получил и принцип Гамильтона, который тут же назвал даже не теоремой, а простым следствием при решение задач на максимум и минимум. Но вот почему так физики ухватились за этот чисто геометрический принцип (теорему), что даже не заметили, что для механики он совершенно не применим. Здесь у меня объяснение только одно «если нельзя, но очень хочется, значит можно». Ведь в ПНД1 этого противоречия с механикой нет – вот и используйте его. Но нет, какой прок революционерам от ПНД1 с его кинетической энергией. Другое дело лагранжиан или гамильтониан с его произвольными изменениями напряженности поля и, следовательно, с реальными скачками энергии. То-то так обрадовался Дирак, когда, рассмотрев вид гамильтоновой функции, какой она принимает для квантовомеханических задач написал

«Мы теперь в состоянии получить все, что требуется для любой механической системы, для которой известна гамильтонова функция H , выраженная через q и p, быть может, зависящая также явно и от t.»

 

 

А вот ПНД1 вполне согласуется с принципами механики. Ведь здесь сравнение на прямых и окольных путях можно выполнять, когда начальная скорость задается одинаковой по модулю, но при этом мы можем сделать и так, что она будет задаваться одинаковой и по направлению на начальном участке пути, чтобы соответствовать принципам механики при сравнение двух путей движения одного и того же тела. А как это будет реализовываться я сейчас рассмотрю на примере задачи заезда грузовика в ворота гаража, которую усиленно рекламировали создатели программы CubiCalc, использующей так называемую «нечеткую логику», которую я рассмотрел в [23]. Правда, на поверку логика у них оказалась самой обычной, но решение задач они делали в духе нормальных героев, которые «всегда идут в обход». И при управление техническими системами они сначала снимают показания с приборов, затем их фаззифицируют и производят с ними действия, а потом дефаззифицируют и опять возвращают в понятном техническим системам виде (то же самое относится и к экономическим системам и всем остальным). Хотя, конечно же, проще без всякой фаззификации и дефаззификации управлять системами с нормальными параметрами и я это показал, создав свою систему управления грузовиком. А на рис.7 Вы видите как грузовик, управляемый этой системой, заезжает из центра машинного двора А’ в ворота гаража А при разных начальных направлениях движения и одинаковой скорости движения (синие линии).

 

 

 

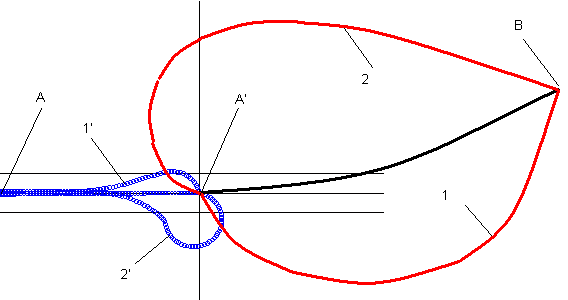
 Рис.7. Заезд грузовика управляемого программой наведения из центра машинного двора A’ в ворота гаража А при разных начальных направление движения (синие линии) и движения тела из точки A’  в точку В по двум окольным путям (красные кривые) и одному прямому (черная кривая).

 

 

Но, если грузовик заезжал в ворота гаража, то мы для ПНД1 можем предложить переходный участок движения тела по различным путям с выездом из гаража. Пусть на всех путях тело у нас на начальном этапе движется из точки А в точку A’, начиная движение в одном и том же направлении и с одной и той же скоростью по синим кривым, что обеспечивается удерживающими связями направляющих, а затем после точки A’ тело продолжает движение или по свободному пути (черная кривая) или по окольным путям, т.е. по направляющим (дуга окружности, парабола, прямая и т.д. красные кривые). При этом, переходный участок этих путей из точки А в точку A’ может быть как угодно мал и, следовательно, в расчетах мы можем сразу считать, что тело вылетает из точки A в произвольном направлении по своему прямому или окольному пути. И таким образом, у ПНД1 пропадает разногласие с принципами механики, согласно которым, при сравнение двух движений одного и того же тела по разным путям, в начальный момент это тело должно иметь и одинаковую скорость и одинаковое направление движения на этих путях. Так что, кому очень хочется, могут на законных основаниях применять ПНД1 и в механике. Остается только вопрос где и зачем. Да, действительно все тела при своем свободном движение стремятся в конце концов достичь минимума потенциальной энергии, хотя при разных исходных данных она вначале может и возрастать. Но в любом случае они всегда движутся с соблюдением всех законов динамики, а на отдельных (локальных) участках этого большого пути кроме этого еще и получается, что такая величина как действие имеет минимальное значение.

 

 

Что по этому поводу можно сказать о минимуме действия. Очень занятно, но не более. Ведь ни в теоретическом плане ни в практическом нам это ничего не дает даже на этих локальных участках пути, границы которых еще надо индивидуально определять. В общем, я бы сказал, что это занятная игрушка, но нам то надо не играться, а решать конкретные задачи, а их  мы можем решить если только опишем движение системы тел дифференциальными уравнениями используя модифицированный мною принцип Даламбера (ни в коем случае не используя уравнения Лагранжа). Вот на этом и надо сосредоточиться преподавателям университетов и при этом не стремится к получению линейных дифференциальных уравнений, чтобы потом забивать студентам головы еще и методами решения этих уравнений. На дворе 21 век и сейчас компьютеры справляются с любыми системами любых дифференциальных уравнений одним универсальным способом – численное решение методом Рунге-Кутта или каким то другим. Ведь нам надо научить студента не решать аналитически учебные задачи, а научить его решать реальные практические задачи. А теперь давайте подведем краткий итог всему сказанному о ПНД, т.е. сформулируем полностью два этих принципа и сделаем выводы, которые вытекают из проведенного исследования.

 

 

Полные формулировки этих двух ПНД будут звучать так. Если при  движение тела или идеальной системы тел в полях потенциальных сил на них не действуют никакие другие внешние силы, которые отклоняют их от свободного пути, т.е. препятствуют такому движению, включая и силы сопротивления среды, то они движутся между двумя точками пути 1 и 2 так, что эти движения характеризуются минимумом такой величины как действие, а величина этого участка пути между точками 1 и 2 определяется так, что конечная точка 2 должна лежать до кинетического фокуса, который для конкретного случая движения определяется индивидуально. При этом если рассматриваем движение тела или системы тел с удерживающими связями, то получается, что на истинном пути, кроме реакций связей не должны действовать никакие другие силы, которые разгоняют тело (систему тел), а потом тормозят (или наоборот), но так, чтобы время движения сохранялось одно и тоже на прямом и окольном пути в формулировке Гамильтона-Остроградского (ПНД2), а в формулировке Эйлера-Лагранжа (ПНД1) затраты энергии на разгон тела (системы тел) были равны затратам энергии на торможение (или наоборот для торможения и разгона).

 

 

А для количественного определения величины действия на локальном участке пути, т.е. между точками 1 и 2 существуют две формулы. В ПНД1 это будет величина определяемая как интеграл от кинетической энергии между моментами времени t1 и t2, которые точка (система тел) проходит в точках траектории 1 и 2, а  в ПНД2 это будет величина определяемая как интеграл от лагранжиана между теми же моментами времени t1 и t2. При этом сравнивать количественно два пути (прямой и окольный) при расчете действия по этим двум формулам надо так, что для ПНД1 начальные скорости в двух этих движениях по модулю должны быть равны, а время движения из точки 1 в точку 2 может быть разным, а в ПНД2 начальные скорости в двух сравниваемых движениях могут быть не равны, но время движения из точки 1 в точку 2 должно быть одинаковым. Еще одним отличием этих двух принципов является то, что ПНД1 можно применять только в том случае если поля потенциальных сил остаются неизменными, т.е. соблюдается закон сохранения энергии и полные энергии на обоих путях будут равны, а ПНД2 можно применять и в том случае, если напряженности этих полей изменяются в функции времени, т.е. может и не соблюдается закон сохранения энергии.

 

 

А выводы будут такими.

1- ПНД1 (Эйлера-Лагранжа) и ПНД2 (Гамильтона-Остроградского) это совершенно разные принципы и объединяет их в отличие от других вариационных принципов только то, что они оба интегральные и у них совпала размерность величины, которую надо минимизировать.

2- Если установить единые правила в вариационном исчисление, то остаться должен только один ПНД, т.к. они оба получаются из одних и тех же исходных данных, но при разных правилах варьирования переменных (изохронное и изоэнергетическое варьирование).

3- ПНД2 не совместим с принципами механики и должен применяться только для решения геометрических задач, т.е. для того, для чего он и создавался Гамильтоном и Остроградским.

4- ПНД1 и ПНД2 являются локальными принципами и чисто математически применимы только на небольших участках путей.

5- ПНД1 и ПНД2 даже чисто теоретически не применимы для решения задач механики, где у нас присутствует трение, а т.к. в реальных механических системах всегда присутствует трение, то по большому счету не применимы в механике никогда.

6- ПНД2, во-первых, не имеет непосредственного отношения к очень сырой гипотезе Фейнмана об интегралах по путям в квантовой механике даже как принцип стационарного действия, а, во-вторых, его просто нельзя использовать для этих целей.

7- Т.к. ОТО Эйнштейна согласуется с ПНД2, а он не согласуется с принципами механики, то ОТО является не механической теорией, а геометрической, т.е. не имеющей ничего общего с реальными процессами, протекающими в Природе. При этом Эйнштейн не имел права выводить уравнения ОТО из ПНД2, т.к. время у него не является независимой переменной и надо было использовать ПНД1.

8- ПНД1 согласуется с принципами механики и может быть рекомендован как развлечение для математиков, которым надо попрактиковаться на каких то идеальных примерах из механики.   

9- Необходимо признать метод получения дифференциальных уравнений, описывающих функционирование механических систем, с использованием лагранжиана нецелесообразным, т.к. он не позволяет описывать реальные механические системы.

10- Необходимо сразу ориентировать студентов на решение дифференциальных уравнений численными методами, т.к. реальные механические системы очень редко описываются линейными дифференциальными уравнениями, которые можно решить аналитически.

11- Следует признать дальнейшее применение вариационного исчисления в механике не целесообразным и использовать его только для решения геометрических задач, т.е. для того, для чего оно и создавалось первоначально.

12- Необходимо рекомендовать университетам страны исключить курс Теоретической физики Ландау и Лифшица из числа учебников.

 

 

Таким образом, мы видим, что само «действие» как таковое не является еще одной универсальной мерой даже для механической формы движения материи, а ПНД не имеет никакого отношения к основным законам динамики и является в лучшем случае только красивыми декорациями, отвлекающими наше внимание от процесса движения тела или системы тел к состоянию наименьшей потенциальной энергии, но является очень любимой игрушкой математиков позволяющей выводить из него уравнения динамики в классической механике для идеальных систем, где эти уравнения и так хорошо известны, а при наличие большой фантазии и всего что угодно в других разделах наук (от физики до социологии). Это и геометрическая теория относительности Эйнштейна с ее геодезическими линиями и интегралы по путям в современной трактовке квантовой механики данной  Фейнманом. Вот только, как признался Фейнман, «квантовой механики не понимает никто», а что касается создателей современных трактовок релятивистской механики, то такого заявления никто из них не сделал, но это не означает, что те, кто пишет о теории относительности, понимают все то, что они пишут, т.к., если говорить о теории относительности, то  надо говорить и о ПНД. А, т.к. туманного смысла этого чисто геометрического принципа никто не понимает в полной мере, то никто ничего не должен понимать и в релятивистской и в квантовой механиках. И это становится особенно очевидно, когда этому принципу придают значение универсального закона над всеми законами Природы, т.е. отводят роль Бога, который управляет физическими процессами в Природе, т.к. пути господни неисповедимы.

 

 

А вот авторы статьи [35] соглашаются, что ПНД не понимает никто, но делают не правильный вод о полезности его применения

«Несмотря на всю исключительность принципа стационарности действия, в настоящее время не существует никаких теоретических разъяснений поразительной успешности и плодотворности его применения, им просто пользуются, ибо реальное движение в физических системах всегда подчиняется ему, а почему — неизвестно.»

А я считаю, что успешно можно применять только то, что ты понимаешь как работает. Например, нашел дикарь гранату и не знает как она работает, но приспособился успешно колоть ей орехи. А в один прекрасный момент взял и дернул за чеку – вот вам и успешное применение. Так что все математико-физики успешно применяющие ПНД это дикари с гранатой.

 

 

Мне могут возразить – ну и что из того, что мы не понимаем, например, и квантовой механики, но ведь позволяет же она нам решать кое-какие задачи и даже предсказала несколько эффектов, значит она правильная наука. Но дело в том, что квантовая механика с ее статистическими методами описывает только то, что уже многократно наблюдали и при этом иногда у нее получается даже что-то новое, но гарантий, что можно с помощью нее сделать еще какие то предсказания нет никаких. По этому не видел никто термоядерного реактора и нет никакой гарантии, что увидим, если все описывать статистическими методами, хотя математико-физики гарантировали создание такого реактора еще 50 лет назад, если будет хорошее финансирование. Деньги им дали, а термоядерного реактора до сего дня так и не видно. А, если его случайно создадут, не понимая как он работает, то возможен и результат как у дикаря с гранатой. И потом, возможность решать кое-какие задачи и делать кое какие предсказания не является доказательством справедливости той или иной теории. Идея теплорода тоже позволяла решать кое-какие задачи термодинамики, но все же была признана ложной. А геоцентрическая теория Птолемея вообще позволяла решать не кое-какие, а все задачи астрономии и в том числе предсказание всех солнечных и лунных затмений на протяжение почти двух тысяч лет и, естественно, считалась единственной правильной теорией.

 

Да, в принципе, таблицами Птолемея можно пользоваться и сейчас, если внести поправку на прецессию. Хотя уже, например, современные солнечные затмения рассчитываются по ним очень с большими ошибками, которые накопились за две тысячи лет. Но можно внести в его таблицы поправки с учетом данных современных наблюдений и они будут опять давать удовлетворительные результаты. Только эти хорошие результаты опять таки не могут быть доказательством геоцентрического строения мира. При этом первые гелиоцентрические таблицы созданные в 17-м веке давали результаты даже хуже, чем таблицы Птолемея созданные во 2-м веке, но Коперник все же предложил свою гелиоцентрическую систему, как он сам говорил, только для того, чтобы расчеты были проще и понятнее, и она оказалась верной. По этому, доказательством истинности той или иной теории может быть только ее простота и понятливость (естественно при возможности описывать и предсказывать на начальном этапе хотя бы часть эффектов). Ведь как сказал Антуан де Сент-Экзюпери "Истина - это вовсе не то, что можно убедительно доказать, это то, что делает все проще и понятнее". А вот как раз с понятливостью у квантовой и релятивистской механик очень большие проблемы.

 

 

А какие же из всего этого можно сделать общие выводы. А вывод тут только один. Если классическая, релятивистская и квантовые механики выводятся из ПНД или обосновываются на его применении, а этого принципа не существует в Природе, то все эти учения являются ложными и должны быть запрещены. Я не настаиваю на законодательном запрете, который, например, по поводу учения Дарвина имеется во многих штатах США, но хотя бы ведущие университеты страны должны убрать эти лжеучения из своих программ. И, конечно же, надо отменить все постановления Академии наук [42], запрещающие критиковать эти учения, а также прикрыть комиссию по борьбе с лженаукой, которая только тем и занимается, что защищает ложные учения. А, если и говорить студентам об этих учениях, то в курсе «Истории механики», куда я бы включил еще и вариационное исчисление, хотя оно и относится к математике. Впрочем, оно и в математике то не очень нужно. Первая вариационная задача (отыскания формы кривой охватывающей наибольшую площадь) была решена еще в Древней Греции и без всякого вариационного исчисления. А все успехи вариационного исчисления сейчас сосредоточены только в механике, т.к. отыскание управляющих функций для придания функционалу заданного значения является для вариационного исчисления не разрешимой задачей. Да, есть принцип максимума Понтрягина, есть динамическое программирование, но всего этого мало. Например, экономике страны нужны эти управляющие функции, чтобы управлять хотя бы ВВП, но математики со своим вариационным исчислением тут бессильны, и при этом закрывают путь для решения этой задачи другим методам.

 

 

Да, конечно, если с завтрашнего дня объявить все эти механики, а вместе с ними и почти всю физику ложными учениями, то в головах многих ученых и студентов это приведет, мягко говоря, к нервному срыву. По этому, конечно же, так резко этого делать нельзя, но надо сейчас хотя бы официально заявить, что да, у нас в современной физике из-за революционных теорий и учений большие проблемы, которые надо будет решать кардинально и надо готовиться к такому решению, когда физика объявит дефолт. Ведь сейчас никто не сомневается, что США, в конце концов, будут вынуждены объявить дефолт, но все страны, а не только США, стараются оттянуть время объявления этого дефолта, по тому что после этого экономикам всех стран мало не покажется. Но здесь то мы видим, что хотя бы экономисты обсуждают эту проблему, т.е. готовятся к такому развитию событий. Вот и научному сообществу надо сейчас обсуждать кризис современной науки и искать пути выхода из него, т.к. когда ни будь и США и физике все же придется объявлять дефолт.

 

 

А в заключение хочу выразить благодарность модератору форума «Большой форум» АИДу, который не только помог мне уточнить многие вопросы, связанные с ПНД, но и является одним из моих оппонентов, которые заставили меня взяться за написание этой статьи.  

 

 

                                                                   Список литературы                                                    

 

1. Л.Ландау, Л.Пятигорский, Механика. – М-Л.: Техтеорлит, 1940. - 200 с.

2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Т.1. Механика. - М.: Физматлит, 1958. - 206 с.

3. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособие в 10-ти т.Т.1. Механика. - 5-е изд. М.: Физматлит, 2004. - 224 с.

4. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособие в 10-ти т.Т.2. Теория поля. - 7-е изд. М.: Физматлит, 1988. - 512 с.

5. Маркеев А.П. Теоретическая механика - 2-е изд. - М.: ЧеРо. 1999, с. 572.

6. Э.Уиттекер, Аналитическая динамика. - М.: Физматлит, 1958. - 586 с.

7. А.И.Лурье, Аналитическая механике. - М.: Физматлит, 1961. - 828 с.

8. Т.Леви-Чевита, У.Амальди, Курс теоретической механики – Т.2. Динамика систем с конечным числом степеней свободы – часть 1. - М.: ИЛ. 1951, с. 572.

9. М. Планк. Принцип наименьшего действия// Вариационные принципы механики/ Под ред. Л.С. Полака, М.: Физматгиз, 1959. с. 580-588.

10. Полак Л.С. Вариационные принципы механики// Вариационные принципы механики/ Под ред. Л.С. Полака, М.: Физматгиз, 1959. с. 780-879. http://ftp.kinetics.nsc.ru/chichinin/pmlic.htm#P

11. А.Эйнштейн  Физика и реальность. М.: Наука, 1965г., 400 с.  

12. А.Пайс. Научная деятельность А. Эйнштейна. М.: Наука, 1989. c. 448.

13. М.В.Остроградский. Дифференциальные уравнения проблемы изопериметров // Вариационные принципы механики/ Под ред. Л.С. Полака, М.: Физматгиз, 1959. с. 315-387.

14. Луи де Бройль Революция в физике - М.: Атомиздат, 1965    http://www.gumer.info/bibliotek_Buks/Science/broil/01.php 

15. У.Гамильтон. Об общем методе в динамике, посредством которого изучение движения всех свободных систем притягивающихся или отталкивающихся точек сводится к отысканию одного центрального соотношения или характеристической функции // Вариационные принципы механики/ Под ред. Л.С. Полака, М.: Физматгиз, 1959. с. 175-234.

16.В.А.Фок Рецензия на книгу Л.Ландау и Л.Пятигорского Механика. Успехи физических наук, 1946, т. XXVIII, вып. 2-3.  http://ufn.ru/ru/articles/1946/2/k

17. К.Гаусс Об одном новом общем принципе механики // Вариационные принципы механики/ Под ред. Л.С. Полака, М.: Физматгиз, 1959. с. 170-172.

18. Лагранж Ж. Аналитическая механика, Т. 1 – М-Л.:  ОНТИ НКТП СССР, 1938. 348 с.

19. Маркеев А.П. О принципе наименьшего принуждения  http://www.pereplet.ru/obrazovanie/stsoros/481.html 

20. Физика для всех. – М.:, Наука, 1974, с.391.

21. Юдин С.Ю. О принципах кратчайшего времени и наименьшего действия  http://modsys.narod.ru

22. Юдин С.Ю. О двух мерах механической формы движения материи. http://modsys.narod.ru

23. Юдин С.Ю. Моделирование систем и оптимизация их параметров. (электронный вариант книги) (http://modsys.narod.ru ) - Волгоград:, 2003. – 208 с.

24. Юдин С.Ю. О формуле Планка и кванте действия  http://modsys.narod.ru

25. Фейнман Р. Вы, конечно, шутите, мистер Фейнман http://lib.aldebaran.ru/author/feinman_richard/feinman_richard_vy_konechno_shutite_mister_feinman/feinman_richard_vy_konechno_shutite_mister_feinman.rtf.zip

26. Фейнман Р. Хибс А. Квантовая механика и интегралы по траекториям / пер. с англ. Э.М.Барлита и Ю.Л.Обухова / под ред. В.С.Барашенкова. - М.: Мир, 1968 - 383 с. http://www.gaudeamus.omskcity.com/lib-pdf/sciences/Fejnman-Hibs_-_KvantovayaMehanikaIntegralyPoTraektoriyam_-_1968_383_PDF.zip

27.Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Т.8. Квантовая механика - М:  Мир, 1977. - 269 с.

28. Слудский Ф.А. Заметка о начале наименьшего действия// Вариационные принципы механики/ Под ред. Л.С. Полака, М.: Физматгиз, 1959. с. 388-391.

29. Д.А.Паршин Г.Г.Зегря Физика. Принцип наименьшего действия. Лекция 28. Научно-образовательного центра ФТИ им. А.Ф.Иоффе  http://phtf.spb.ru/files/lect28h.pdf  

30 К.Холл «Надо меньше думать об основах»: Курс теоретической физики Ландау и Лифшица в культурно-историческом контексте  www.ihst.ru/projects/sohist/papers/iifm/2004/156-205.pdf

31. М.Бессараб. Лев Ландау роман-биография http://lib.rus.ec/b/316039/read

32. П.В.Куракин, Г.Г.Малинецкий Как пчелы могут объяснить квантовые парадоксы. Институт прикладной математики им. М.В.Келдыша РАН. http://quantum3000.narod.ru/my_papers/intro.html

33. Г. Корн, Т. Корн. Справочник по математике (для научных работников и инженеров), М.: Наука, 1974, 832 с.

34. Б.И.Макаров Законы управляющие вселенной, Часть 1, Глава 2, §8 Интегральные и дифференциальные вариационные принципы механики (электронный вариант книги)   www.energy-source.ru/kniga/kniga-ch1/142-integral-princip.html   - Тверь.

35. И.З.Цехмистро, В.И.Штанько и др. «КОНЦЕПЦИЯ ЦЕЛОСТНОСТИ». – Харьков: Изд-во Харьковского гос. ун-та, 1987. http://psylib.org.ua/books/koncelo/txt01.htm
36. О.С.Разумовский. Методологические проблемы экстраполяции и инверсии (вариационные принципы в науке). Новосибирск.: Институт философии и права СО РАН, 1995.  http://ihtik.lib.ru/2011.07_ihtik_articles-thesis/2011.07_ihtik_articles-thesis_6191.rar

37. Г.Герц Принципы механики, изложенные в новой связи. – М.:  АН СССР, 1959. – 385 с     

38. А.Зоммерфельд  Механика. – М.-Ижевск: Регулярная и хаотическая динамика, 2001. - 368 с.                     39. А.А.Тяпкин Об истории возникновения «теории относительности»  http://www.h-cosmos.ru/papers/thist.htm      

40.  П. Гербер Пространственное и временное распространение гравитации http://bourabai.narod.ru/articles/gerber/gerber-rus.htm 

41. В.Кулигин, Г.Кулигина, М.Корнева Вариационный принцип релятивистских теорий http://n-t.ru/tp/ns/krt4.pdf

42. Ю.Бровко Политика в науке? или: наука орудие политики?  http://tsarstvo999.narod.ru/Brovko/polit10.htm