г. Волгоград, ООО Научно-производственный центр “Микродюйм”

Сейчас очень часто и многие используют слово “модель”, но, к сожалению, не всегда грамотно, когда это касается не модели (типа, марки) автомобиля или модели (образца) платья, а модели объекта, который надо оптимизировать или исследовать используя эту модель. И в этом случае под моделью следует понимать копию объекта, находящуюся с ним в определенном объективном соответствии, способную замещать его на определенных этапах познания и практической деятельности человека и дающую при ее исследовании информацию о самом моделируемом объекте, т.е. оригинале. При этом под объектом в смысле объективной реальности следует понимать различные системы: механические, физические, биологические, социально-экономические и т.д., а под системой следует понимать ограниченное множество элементов объединенных причинно-следственными и функциональными связями, позволяющими ей функционировать определенным образом. Если охарактеризовать объект с точки зрения теории отражения, то он подвергается внутренним и внешним воздействиям и реагирует на них изменением своего состояния в виде различных показателей работы.

Наличие в моделях логической структуры позволяет не только прогнозировать показатели работы системы, но и экстраполировать выводы, вытекающие из структуры модели, на структуру самого объекта. Так, когда было установлено, что в уравнении Дирака имеются корни противоположных знаков, то при экстраполяции этих выводов на оригинал, был сделан прогноз, что наряду с отрицательно заряженным электроном должна существовать симметричная электрону частица с положительным зарядом, антиэлектрон, т.е. позитрон. Эта частица была позже обнаружена в опытах Андерсена. Но как часть модели, логически увязанная с ее другими частями, может быть использован и любой имитатор. Это замечание является очень важным и позволяет использовать, например, при моделировании социально-экономических систем наряду с экспертными системами и имитаторы элементарного интеллекта [1,2] при нахождении оптимальной стратегии действий человеком, являющимся частью модели.

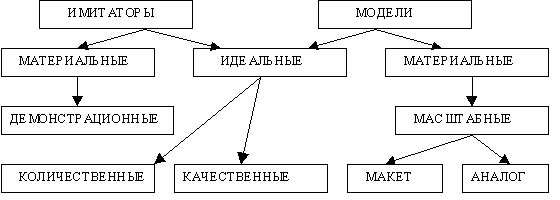
Все существующие классификации моделей очень запутаны и в них, естественно, нет деления на модели и имитаторы, поэтому рассмотрим классификацию моделей и имитаторов, предлагаемую мною и представленную на рис.1. Как модели, так и имитаторы будем разделять на материальные и идеальные. Идеальные модели и имитаторы, в отличие от материальных, состоят не из вещественных элементов, а свойства оригинала описаны в них с помощью цифр, функций, логических построений и образов предметов и ситуаций.

Рис.1 Классификация моделей и имитаторов.

Материальные модели систем состоят из вещественных элементов, природа которых, как правило, одинакова с природой оригинала и реализуются они на основе теории подобия. В основе этой теории положена, развивающая теорему Ньютона о подобии, предпосылка, согласно которой два явления подобны, если по данной характеристике одного явления можно получить характеристику другого простым пересчётом, аналогичным переходу от одной системы единиц измерения к другой или простым пересчётом масштаба. Таким образом, материальные модели, как правило, являются уменьшенными копиями оригинала. Обычно их называют макетами. Это может быть макет самолёта, продуваемый в аэродинамической трубе или макет гидроэлектростанции прокачиваемый на стенде и т.д. Но не надо их путать с демонстрационными имитаторами, которые могут быть выполнены с несоблюдением масштаба и их природа может отличаться от природы оригинала. Так материальные демонстрационные имитаторы атомов химических элементов выполняются без соблюдения масштаба и шарики, обозначающие протоны или электроны, состоят не только из них. Кроме того, на этих имитаторах нельзя проводить никаких экспериментов, точно так же, как и на демонстрационных имитаторах молекул углеводородов.

Другой класс масштабных моделей представляют аналоговые модели, которые в литературных источниках называют модель-аналог. Эти материальные модели тоже реализуются на основе теории подобия и состоят из вещественных элементов, но природа этих элементов существенно отличается от природы оригинала. В основе этих моделей лежит математический изоморфизм, т.е. дифференциальные уравнения, описывающие процессы протекающие в модели идентичны уравнениям описывающим процессы протекающие в оригинале. На этих моделях также как и на макетах можно не только проводить демонстрационные опыты как на материальных имитаторах, но и производить оптимизацию параметров системы. При этом оптимизацию можно проводить только в тех интервалах изменения параметров (как и у макетов), пока фактор масштаба не повлияет на характер протекания процессов.

Например, при оптимизации параметров гидравлической системы можно заменить её электрической, зная при каких параметрах будет ламинарное течение жидкости, а при каких турбулентное и аналогом напора в гидравлической модели будет напряжение в электрической и т.д. В настоящее время аналоговые модели практически не используются ни для каких целей, хотя, например, используя электрическую аналоговую модель, можно удовлетворительно смоделировать паводок на Волге с её каскадом ГЭС, также как и используя гидравлический макет. Однако, их не надо путать с электронными аналоговыми вычислительными машинами, которые пока ещё иногда используются, а перспективные на сегодняшний день нейрокомпьютеры по своей природе тоже являются аналоговыми и поэтому в них вместо электрической схемы можно использовать оптическую и не только для передачи информации, но и для её обработки. Материальные модели и имитаторы пока еще тоже используются в практической деятельности человека, но с появлением электронных цифровых вычислительных машин особое внимание сейчас приковано, конечно же, к идеальным моделям и имитаторам.

Идеальные как модели, так и имитаторы, делятся на количественные и качественные, так же как и задачи исследования операций. И хотя, человеческий мозг при принятии решений использует воображаемую модель, в которой имеются как качественные параметры, так и количественные одновременно и которые закодированы в мозгу одним и тем же индивидуальным кодом, мы пока еще не научились делать ни качественные, ни смешанные модели, но уже есть положительные результаты при решении некоторых качественных задач исследования операций с использованием нейрокомпьютеров. Количественные модели - это математические модели (ММ), построенные на законах стандартной логики и в их основе всегда лежат законы. Если в их основе заложены объективные законы, т.е. законы Природы, то данная модель всегда обладает прогностической функцией, т.е. с помощью нее мы можем прогнозировать будущее. Если же в модели имеются как объективные, так и субъективные законы, т.е. законы поведения человека или законы налогового кодекса, то прогнозировать будущее с помощью таких моделей можно только с какой-то вероятностью в расчете на то, что эти законы либо не будут меняться, либо будут меняться по известным нам правилам.

Все известные нам законы не являются абсолютной истиной и даже законы Евклидовой геометрии, державшиеся более двух тысяч лет, рухнули с появлением в ХIХ веке Лобачевского. Следовательно, модели могут состоять не только из законов в строгом их понимании, но и более простых математических зависимостей, отражающих определенным образом взаимосвязь различных явлений, на доступном нам на сегодняшний день уровне. Но, в основе ММ должны лежать законы, которые вместе с этими простейшими зависимостями, назовем их аппроксимациями, т.е. математическими имитаторами (МИ), должны быть логически все объединены в единую систему. И чем больший процент математических формул, входящих в ММ будут составлять законы, а не эмпирические зависимости, тем достовернее будет прогноз на будущее. Таким образом, любая ММ отражает условность уровня познания достигнутого ее создателем и, следовательно, она обязательно должна содержать в себе способность к расширению и модификации, когда отдельные явления, не учтенные или слабо отраженные в модели, могут быть учтены при дальнейшей работе с моделью, если это потребуется для достижения другой цели операции. При этом, в отличие от имитаторов, переделывается не вся модель, а только один ее элемент.

Чаще всего динамические МИ описываются набором передаточных функций, полученных в результате идентификации оригинала и имитатора. При этом сам объект рассматривается как “черный ящик” с неизвестной структурой и требуется подобрать такую передаточную функцию, чтобы сигналы, которые регистрируются на выходах оригинала и имитатора, были идентичны при одних и тех же сигналах на их входах. Но беда в том, что люди использующие имитаторы, считают их моделями со всеми вытекающими отсюда последствиями их применения, например, для прогнозирования в финансовом мире. У экономистов такие имитаторы называются трендовыми моделями на основе кривых роста, так как их основной задачей является сделать прогноз о развитии изучаемого процесса на предстоящий период времени, т.е. проследить тренд. Но точно также как имитаторы Птолемея или Кеплера не могут сказать в какую сторону полетит Марс, если к нему уже приближается огромный астероид, не могли ответить и все биржевые имитаторы куда полетит курс ГКО, когда уже приближался дефолт 1998 года.

Литература

1. Юдин С.Ю. Моделирование систем и оптимизация их параметров. - Волгоград: Электронный вариант книги (http://ser.t-k.ru), 2003. - 208с.