|
Скорость гравитации
|
|
| modsys | Дата: Вторник, 18.06.2013, 20:12 | Сообщение # 1 |
 Рядовой
Группа: Администраторы
Сообщений: 13
Статус: Offline
| Предлагаю обсудить вопросы рассмотренные мною в цикле статей "Скорость гравитации", но прошу задавать вопросы только по тексту статей, а не на отвлеченные темы. При этом, приветствуется не более одного сообщения за несколько дней, так что думайте прежде чем что-то спросить или что-то ответить. Мне здесь не нужна высокая посещаемость или активность участников обсуждения. Мне нужно серьезное и вдумчивое обсуждение, подразумевающее, что участники обсуждения знакомы с моими статьями.
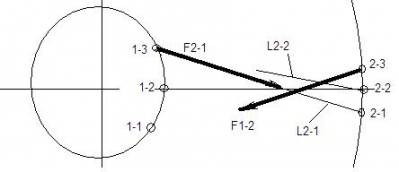
Вот, например, как будут взаимодействовать Меркурий и Венера при конечной скорости гравитации (см. рисунок) и в результате будет нарушаться 3-ий закон Ньютона. А, как следствие будут нарушаться и закон сохранения механической энергии системы и закон сохранения момента количества движения системы, но отрицать конечность скорости гравитации бессмысленно, также как конечность скорости света или звука или электростатического взаимодействия между телами. Правда, в ОТО все эти законы тоже нарушаются, но по совершенно другой причине, которую я считаю надуманной.
Но все существующие теории гравитации строились исходя из отсутствия запаздывания по координатам (это потенциалы Вебера, Гербера, Лиенара-Вихерта), т.е. де-факто в них принималась скорость гравитации равная бесконечности. При этом я извиняюсь, что в статье ошибочно считал, что у самих Лиенара и Вихерта были тоже потенциалы запаздывающие по координатам, а Ландау и Фейнман исказили их идею. Нет, сейчас я нашел подлинник статьи Лиенара и понял, что у него именно те потенциалы, которые описывают Ландау и Фейнман. А о том, что надо учитывать конечность скорости гравитации и использовать потенциалы запаздывающие по координатам писали, например, Лаплас и Эддингтон, но сейчас про эти потенциалы стараются даже не упоминать. Вот и в ОТО вроде бы как учитывается конечность скорости гравитации, но для второстепенных и фиктивных преобразований, а такой мощный эффект, как запаздывание по координатам, не учитывается. Да и все остальные теории (часть я привожу в таблице), также, как и ОТО, создавались не исходя из общих предпосылок и здравого смысла, а целенаправленно для объяснения одного единственного эффекта – дополнительного (к теории Ньютона) смещения перигелия Меркурия и поэтому у них полностью отсутствуют дополнительные к теории Ньютона смещения других параметров орбит планет (кроме чисто астрономической теории Зеелингера).
Вид данных___________________Меркурий Венера Земля Марс
Наблюдения (Ньюком)___________575,06___42,52___1162,92___1602,69
теория Ньютона (Ньюком)_______533,82___49,85___1156,95___1594,65
Аномальный остаток (Ньюком)___41,24___-7,33______5,97______8,04
теория Холла (Ньюком)__________43,37___16,98____10,45______5,55
теория Эйнштейна (Субботин)____43,03____8,62_____3,83_____1,35
теория Гербера (Хайдаров)_______43,03____8,62_____3,83_____1,35
теория Ритца k=6,4 (Роузвер)_____41,0_____8,0______3,4_______-
теория Маха (Зайцев)____________43,0____23,0_____17,0_____11,0
теория Зеелингера (Роузвер)_____41,3_____7,3______4,2______6,3
Например, согласно уточненным мною данным в покоящейся Солнечной системе теория Ньютона (при скорости гравитации равной бесконечности) дает для Меркурия смещение перигелия 529 угл.сек за 100 лет, а ОТО дает 572 угл.сек, т.е. эффекты ОТО добавляют 43 угл.сек. Примерно такой же результат, как и по теорииНьютона, будет и при учете запаздывания по координатам и расчете силы притяжения по Ньютону при скорости гравитации равной уже скорости света, но в покоящейся Солнечной системе. А, если принять абсолютную скорость Солнечной системы несколько сотен километров в секунду, а такая скорость никем не оспаривается, то при скорости гравитации равной скорости света получаются смещения перигелия Меркурия в тысячи угл.сек за 100 лет, что никак не соответствует наблюдаемым данным, которые по разным оценкам составляют 572…578 угл.сек.
Отсюда вывод, чтобы обеспечить такое смещение, скорость гравитации должна быть гораздо больше скорости света, а все существующие теории являются надуманными теориями не имеющими к реальности никакого отношения и, например, ОТО при любой скорости Солнечной системы дает те же 43 угл.сек. При этом, на смещение других параметров орбит планет (эксцентриситет, угол наклона и т.д.) она не оказывает никакого влияния, а они при скорости Солнечной системы не равной нулю и при учете запаздывания по координатам тоже получаются очень большие. Более того, если учитывать запаздывание по координатам, то получается, что инерциальных систем отсчета не существует и при разной скорости Солнечной системы будут разные смещения параметров орбит планет. Вот я и хочу подобрать такую скорость гравитации и такую скорость Солнечной системы, чтобы с использованием формулы тяготения Ньютона и учета запаздывания потенциала по координатам наблюдаемые данные соответствовали расчетным. Какие будут вопросы или замечания по предлагаемой мною методике поиска скорости гравитации.
С наилучшими пожеланиями Сергей Юдин.
|
| |
| |
| nymos | Дата: Понедельник, 14.10.2013, 17:38 | Сообщение # 2 |
|
Рядовой
Группа: Пользователи
Сообщений: 1
Статус: Offline
| Четвертая статья цикла «Скорость гравитации» имеет 10 параграфов, включая выводы, и приложения. Рассмотрим каждый из параграфов последовательно (отдельный пост).
В первом параграфе («Эффект запаздывания потенциала по координатам») автор на 10 страницах излагает различные методы учета конечной скорости распространения взаимодействия, применительно к «запаздывающему потенциалу». Приводится также итерационный алгоритм расчета временной задержки и результат тестового расчета (рис.3), схематически анонсированного на рис.1.
Из текста данного параграфа не ясно, как именно автор использовал «запаздывающий потенциал» (в форме (2), или (3)) для проведения динамических расчетов, результаты которых приведены в таблицах данного раздела.
По косвенным замечаниям из текста можно понять, что автор использует время запаздывания для расчета актуального («запаздывающего») радиуса взаимодействия, которое и подставляет в формулу (1) вместо R.
Если это так, то, во-первых, мне это представляется логично вытекающим из схемы рис.1, а во-вторых, становятся непонятными причины скрупулезного обсуждения резонов вокруг «запаздывающего потенциала».
В связи с этим отмечу, что задача построения векторного поля кулоновского типа, которое распространяется в пространстве с конечной скоростью от движущегося объекта – это чисто геометрическая задача, имеющая точное решение. http://yadi.sk/d/igRl2DP3Awb3v
Иными словами, при известной траектории движения тела, в каждый момент времени существуют аналитические выражения для силы, как векторной функции, заданной в каждой точке пространства. Причем такой, что отрезок прямой, проведенный из любой точки в направлении заданного в ней вектора поля до пересечения с траекторией движения тела, преодолевается со скоростью распространения взаимодействия за то же время, что и тело проходит свой путь по траектории от точки пересечения до положения в выбранный момент. При этом абсолютная величина силы определяется по длине этого отрезка (для гравитации – обратно пропорционально ее квадрату).
За неимением прямой ссылки названные формулы я отправил в личном сообщении.
Из них, в частности, следует, что гравитационное поле движущегося тела является вихревым в случае конечной скорости его распространения. По этой причине оно не может являться следствием лишь одной скалярной функции φ.
Кроме того, тестовые расчеты показывают, что орбита пробного тела, движущегося в поле запаздывающей гравитации, непрерывно вращается и увеличивается в размерах. По этой причине я согласен с автором, что одного лишь запаздывания по координатам не достаточно, для построения теории эволюции планетных орбит.
Авторское изложение концепции Вебера можно найти здесь (стр. 311 и далее).
http://gallica.bnf.fr/ark:/12148/bpt6k95189w.r=+Weber%2C+Wilhelm+Eduard.langFR
Добавлено (14.10.2013, 17:14)
---------------------------------------------
Продолжение 1.
Второй параграф статьи - «Эффект динамического давления потенциалов», фрагментирован, и состоит из трех подразделов. Автор начинает изложения с анализа влияния скорости движения тел на гравитационные силы, сравнивая формулы Вебера и Гербера, а заканчивает собственной формулой и объяснением метода ее получения.
В данном параграфе, в отличие от предыдущего, основное внимание уделяется предполагаемому влиянию скорости движущихся объектов на абсолютную величину гравитационной силы, а не ее направление.
Автора интересует вопрос, почему формулы Вебера и Гербера совпадают, несмотря на то, что они были получены исходя из принципиально различных исходных предположений. А именно: в одном случае конечность скорости распространения взаимодействия не учитывалась (Вебер), а в другом – читывалась (Гербер).
Кроме этого автора заботит причина появление в этих формулах ускорения (сила зависит от силы) и он ищет путь избавиться от него.
Объективности ради следует признать, что наш предшествующий опыт учета влияние скорости на величину статических сил в процессе движения, в целом является негативным.
Можно сказать, что эта деятельность была инициирована Ньютоном в том разделе «Начал», где рассматривалось внутреннее трение в текучей среде. Ньютон высказал предположение, что сила внутреннего трения обусловлена «скоростью разбегания частиц жидкости». Эту гипотезу в последствии использовал Навье при выводе уравнения движения несжимаемой жидкости. А именно, он предположил, что при относительном движении молекул, сила их «упругого» взаимодействия возрастает при сближении и уменьшается при удалении в зависимости от величины скорости. Эта его работа была обнародована в марте 1822 года. Уравнение Навье не утратило актуальности и сегодня.
Пуассон, в октябре 1829 году, предпринял попытку объяснить внутреннее трение в жидкости, не привлекая гипотезу Ньютона. Но эта попытка дала негативный результат. Поэтому им была выдвинута гипотеза о запаздывающем действии сил давления в движущейся среде. Этот, последний, результат используется в теории сжимаемых течений.
Вебер, по существу, рассматривает ту же задачу, что и Навье – взаимодействие параллельно движущихся потоков частиц. Отличие состоит лишь в том, что Навье интересовала сила в направлении движения потока, а Вебера – перпендикулярно движению, поскольку он пытался объяснить закон Ампера о силе взаимодействия проводников с током. Он приходит к выводу, что для встречных потоков заряженных частиц, предполагаемое влияние скорости их относительного движения на электростатическую силу не должно зависеть от направления скорости. Для учета же взаимодействия потоков частиц, расстояние между которыми не изменяется, он предложил ввести ускорение. Так был формально описан эффект электромагнитной индукции.
Впоследствии, силы внутреннего трения в ламинарных потоках жидкости нашли свое объяснение как результат молекулярной диффузии, а закон взаимодействия токов в проводниках – как следствие электромагнитного взаимодействия.
В итоге, на настоящий момент, у нас нет действующих теорий, объясняющих изменение силовых полей скоростью движения объектов их динамического влияния. Исключение составляет теория конечной скорости распространения взаимодействий.
Добавлено (14.10.2013, 17:38)
---------------------------------------------
Продолжение 2.
Вернемся теперь к анализу формулы Вебера-Гербера (в тексте (5) и (6), соответственно) и авторскому варианту (формула (25)). Не трудно заметить, что формулы (5) и (6) отличаются лишь величиной скорости распространения взаимодействия. У Гербера она в корень из 6 раз меньше, чем у Вебера. В этой связи, то обстоятельство, что вариант Гербера дает больший эффект при расчетах смещения перигелия Меркурия, чем формула Вебера, представляется естественным. Поскольку увеличение скорости распространения взаимодействия до бесконечности полностью нивелирует эффект ее влияния.
В силу перечисленных причин, формулы (5) и (6) могут быть объединены для последующего анализа в одно выражение, включающее неопределенную скорость с.
Формула же (25) принципиально отличается от варианта Вебера-Гербера: в ней отсутствует ускорение, а скорости движения взаимодействующих тел не являются относительными, как это обозначено у предшественников. Поэтому к ней мы вернемся позже.
Итак, считается, что формула Вебера-Гербера является следствием двух различных по виду модифицированных потенциалов (8) и (9). При этом: для вывода (5), потенциал (8) используется как составляющая функции Гамильтона, а при выводе (6), потенциал (9) – компонент функции Лагранжа. Далее, можно убедиться, что если (8) использовать для построения лагранжеана, а (9) для гамильтониана, то ни формула (5), ни формула (6) не будут получены. Такой результат вызывает недоумение.
Описанное противоречие полностью устраняется путем нахождения явного вида функции Гамильтона из уравнений движения, где в качестве силы выступает выражение (5). Для этого их разрешают относительно вектора ускорения w=dv/dt
w
= –G.r(c2 – (v.v))/[ R2(c2R+2G)]
= –G.r(c2 – (v.v))/[ R2(c2R+2G)]
R = (r.r)1/2
R = (r.r)1/2
Соответствующие полученным уравнениям функции Гамильтона H(r,v) и Лагранжа L(r,v) имеют вид
H(r,v) = -c2{ln(c2-(v.v)) + [ln( R )-ln(c2R+2G
)]}
)]}
L(r,v) = -c2 {ln(c2-(v.v)) - [ln( R )-ln(c2R+2G
)]}
)]}
Теперь уравнения движения могут быть получены и как уравнения Гамильтона и как уравнение Эйлера. Причем, итог обеих подходов идентичен.
Представленный результат свидетельствует о целесообразности учитывать влияние различных факторов именно на силу взаимодействия, как это делал Вебер.
Теперь, что касается формулы (25), то в отношении нее имеется много вопросов. Обозначим три из них.
1. При выводе формулы автор полагает, что если мощность (скалярная величина) есть скалярное произведение вектора силы и вектора скорости, то из этого равенства можно определить силу. Однако это не так. Для решения данной задачи нужно иметь дополнительно выражение для векторного произведения силы и скорости, поскольку оно входит в искомое выражение для вектора силы.
2. Нельзя не учитывать, что скорость распространения взаимодействия ни в акустике, ни в электродинамике, собственно скоростью не является. Там это некоторая комбинация свойств среды, которая имеет размерность скорости. Свойства среды от ее перемещения, или перемещения чего-либо в ней, не зависят. По этой причине сопоставлять эту величину с кинетической скоростью, которая не абсолютна, а отсчитывается относительно некоторой системы отсчета, методически не корректно.
3. Принимая во внимание относительный характер скорости движения, из текста статьи не ясно, что конкретно понимает автор под скоростями движения i-го и k-го тела в формуле (25).
Сообщение отредактировал nymos - Понедельник, 14.10.2013, 23:00 |
| |
| |
| modsys | Дата: Суббота, 25.04.2015, 19:00 | Сообщение # 3 |
 Рядовой
Группа: Администраторы
Сообщений: 13
Статус: Offline
| Чтобы не возникало вопросов почему я оставил это сообщение без ответа, надо пояснить, что Алексей его отправил сюда по ошибке и с большим опозданием, т.к. у нас была договоренность, что я высылаю ему черновой вариант статьи (до публикации), а он мне по электронной почте свои замечания в виде рецензии, чтобы я их учел при публикации статьи (сейчас опубликована уже и первая и вторая редакции). В личном письме я ему указал на это и дальнейших его сообщений мы тут не видим, но первое его сообщение я не стал убирать (хотя, наверное, надо бы было убрать). Теперь вот надо будет дать пояснения по его замечаниям и тут, что я сейчас и сделаю.
Цитата nymos (  ) Из текста данного параграфа не ясно, как именно автор использовал «запаздывающий потенциал» (в форме (2), или (3)) для проведения динамических расчетов, результаты которых приведены в таблицах данного раздела. По косвенным замечаниям из текста можно понять, что автор использует время запаздывания для расчета актуального («запаздывающего») радиуса взаимодействия, которое и подставляет в формулу (1) вместо R.
Если это так, то, во-первых, мне это представляется логично вытекающим из схемы рис.1, а во-вторых, становятся непонятными причины скрупулезного обсуждения резонов вокруг «запаздывающего потенциала».
Ну, естественно, я вел расчеты по формуле (2) и там же я и пишу как я это делал за несколько итераций (см. код), т.к. формула (2) дает только первое приближение. А различные запаздывающие потенциалы», которые были известны до меня, я рассматриваю, чтобы показать отличие моей формулы (2) и далее формулы (25) от существовавших до этого.
Цитата nymos (  ) В связи с этим отмечу, что задача построения векторного поля кулоновского типа, которое распространяется в пространстве с конечной скоростью от движущегося объекта – это чисто геометрическая задача, имеющая точное решение. http://yadi.sk/d/igRl2DP3Awb3v
Вот только тут есть маленькое препятствие. Унас до решения задачи с использованием запаздывающих потенциалов почему то НЕ известна траектория движения тела.
Цитата nymos
В итоге, на настоящий момент, у нас нет действующих теорий, объясняющих изменение силовых полей скоростью движения объектов их динамического влияния. Исключение составляет теория конечной скорости распространения взаимодействий.
Вот и замечательно, т.к. моя теория как раз и строится на конечной скорости распространения взаимодействий.
Цитата nymos (  ) Представленный результат свидетельствует о целесообразности учитывать влияние различных факторов именно на силу взаимодействия, как это делал Вебер.
Ну, вообще то, как Вы не могли не заметить, у меня и поформуле (2) рассчитывается радиус, чтобы потом посчитать силу, и по формуле (25) рассчитывается сила, поэтому не понятно зачем сделан этот вывод, подтверждающий мои расчеты, как замечание (может быть это обоснование моего подхода, а не замечание).
Цитата nymos
Теперь, что касается формулы (25), то в отношении нее имеется много вопросов. Обозначим три из них. 1. При выводе формулы автор полагает, что если мощность (скалярная величина) есть скалярное произведение вектора силы и вектора скорости, то из этого равенства можно определить силу. Однако это не так. Для решения данной задачи нужно иметь дополнительно выражение для векторного произведения силы и скорости, поскольку оно входит в искомое выражение для вектора силы.
2. Нельзя не учитывать, что скорость распространения взаимодействия ни в акустике, ни в электродинамике, собственно скоростью не является. Там это некоторая комбинация свойств среды, которая имеет размерность скорости. Свойства среды от ее перемещения, или перемещения чего-либо в ней, не зависят. По этой причине сопоставлять эту величину с кинетической скоростью, которая не абсолютна, а отсчитывается относительно некоторой системы отсчета, методически не корректно.
3. Принимая во внимание относительный характер скорости движения, из текста статьи не ясно, что конкретно понимает автор под скоростями движения i-го и k-го тела в формуле (25).
1- Теоретизировать можно сколько угодно,но практически в своих расчетах эту силу я нахожу.
2- В том то и дело, что у меня это какраз и есть скорость с которой изменяются свойства среды, в которой движется пробное тело, поэтому не понятен смысл замечания.
3- Я понимаю абсолютныескорости этих тел в среде (эфир, кефир и т.д.).
P.S. Если у кого то возникли другие столь же аргументированные замечания по статье, то буду благодарен, если Вы их озвучите.
С наилучшими пожеланиями Сергей Юдин.
|
| |
| |
| aeromash | Дата: Среда, 29.01.2020, 10:10 | Сообщение # 4 |
|
Рядовой
Группа: Пользователи
Сообщений: 1
Статус: Offline
| День добрый!
Давайте решим не сложную задачу.
В предположении, что на Меркурий действует некоторая не учтенная сила, найдем аномальное ускорение вызываемое этой силой, вызывающее аномальный сдвиг перигелия Меркурия равный 43" за сто лет?
Вы будете удивлены.
Могу сразу дать ответ на эту задачу. Информация к размышлению:
1. Аномальное ускорение Меркурия а=1.2122*10^-10 м/с^2
2. Аномальное ускорение зондов "Пионер" а=1.3*10^-10 м/с^2 (необъяснимый остаток)
3. Центростремительное ускорение Солнца в галактике V^2/R~1.2*10^-10 м/с^2
4. Константа Милгрома или аномальное ускорение звезд в рукавах спиральных галактик а=1.2*10^-10 м/с^2
5. Произвдение скорости света на константу Хаббла сН~а=7*10^-10 м/с^2
6. Ускоренное "расширение" Вселенной а=1.2*10^-10 м/с^2
7. Ускорение необходимое для достижения скорости света и границы Вселенной за время ее жизни а=1.2*10^-10 м/с^2
Вывод:
Аномальный сдвиг Меркурия вызван не внутренними особенностями солнечной системы, а внешним неучтенным глобальным фактором, самой Вселенной. Поэтому ответы на локальные вопросы перигелиев лежат за пределами солнечной системы и даже за пределами нашей галактики.С уважением, Юрий!REPLY
Сообщение отредактировал aeromash - Среда, 29.01.2020, 16:45 |
| |
| |









