………………….              ……    СКОРОСТЬ ГРАВИТАЦИИ

                            Часть 2 -  КИНЕМАТИЧЕСКАЯ ТЕОРИЯ ПЛАНЕТ

 

………………………………….первая редакция 09.04.2012                                                                                 

 

С. Ю. Юдин                       …http://modsys.narod.ru                    modsys@narod.ru

 

 

В первой части этого цикла статей я упомянул, что древние астрономы использовали для создания своих теорий кинематическую методику, а современные астрономы используют динамическую, т.е. с использованием физических законов (можно еще сказать, что физическую метододику). Таким образом, я считаю, что в настоящее время с различными вариациями известны две методики определения параметров орбит планет по наблюдательным данным. Типичными результатами применения первой методики являются теория Птолемея и законы Кеплера, а второй аналитические теории планет Леверье и Ньюкома (New2) и полученные численными методами эфемериды JPL2 (JPL – лаборатории реактивного движения, подразделение НАСА), которые представлены аппроксимациями в файлах DE405. А т.к. классификации этих методик я нигде не встречал, то, во-первых, мне пришлось дать им названия - кинематическая и динамическая (физическая), а, во-вторых, мне же придется и указать на их отличия. До тех пор пока в 1665 году Ньютон и в 1680 году Гук (не зависимо от Ньютона) не пришли к выводу, что сила притяжения между телами обратно пропорциональна квадрату расстояния, а в 1687 году Ньютон в своих Началах не свел воедино имеющиеся на тот момент представления о законах движения тел, которые сейчас известны как три закона Ньютона, физических методик быть не могло.

 

 

Таким образом, даже Коперник, опубликовавший в 1545 году свою гелиоцентрическую теорию строения Солнечной системы, использовал кинематическую методику с теми же деферентами и эпициклами, что и Птолемей. И Кеплер, открывший в 1609 году два своих первых закона и в том числе о движение планет по эллипсам, тоже использовал чисто кинематическую методику, аппроксимируя различными геометрическими фигурами данные наблюдений. Здесь надо так же заметить, что и сама методика решения различных задач вплоть до 17 века была геометрической, т.е. задачи решались с помощью циркуля и линейки или простейших геометрических соотношений, и этой методикой решения математических задач, пользовался даже Ньютон в своих Началах. Но после того, как в 1684 году Лейбниц (не зависимо от Ньютона) дал систематическое изложение дифференциального исчисления, а в 1686 и интегрального исчисления, математические задачи стало не только намного проще решать, но и появилась возможность решать такие сложные задачи, как описание движения планет с использованием физических законов. А после теоретических работ таких великих математиков прошлого, как Эйлер, Лагранж, Лаплас и Гаусс все эти математические методы стали доступны и астрономам. И вот здесь в методику определения параметров орбит вклинилось лишнее звено – физическая теория.

 

 

Если Птолемей, аппроксимируя данные наблюдений, находил непосредственно параметры круговых орбит в геоцентрической системе координат (например, радиусы эпициклов и деферентов), предполагая равномерное вращение различных сфер с этими параметрами, и Кеплер определял непосредственно параметры эллиптических орбит в гелиоцентрической системе координат (например, эксцентриситет и большую полуось), предполагая движение планет по эллипсам со скоростями в соответствие с найденным им чисто кинематическим законом площадей, то Леверье с Ньюком и сотрудники JPL поступали иначе. Они по данным наблюдений находили оптимальные параметры их математических моделей, построенных с использованием физических теорий, где использовалась та или иная модификация закона притяжения Ньютона. Вот только какие методы оптимизации они при этом использовали мне не известно, но в результате этого, например, Леверье в теории движения каждой из внутренних планет получал при этом различные оптимальные значения для масс трех других планет земной группы.

 

 

При этом Леверье и Ньюком, при решение дифференциальных уравнений, использовали аналитические методы, а сотрудники JPL численные, что с применением ЭВМ делает эту задачу не сложной. При аналитическом решение, т.к. системы, состоящие из более чем двух тел, не решаются аналитически (задача трех тел), для каждой планеты решают отдельную задачу. При этом в правой части  дифференциального уравнения, кроме силы притяжения от Солнца, записывается еще так называемая пертурбационная функция, которая учитывает силы притяжения от других планет и которая вычисляется заранее, а после первого шага решения она уточняется, что делает вычисления очень трудоемкими. А при численном решение решают сразу всю систему дифференциальных уравнений, описывающую движение всех планет и воздействие всех планет друг на друга определяется непосредственно во время решения уравнений, после каждого шага решения (итерации).

 

 

Но у аналитического метода есть и одно преимущество перед численным, т.к. при численном решение мы можем оптимизировать только параметры модели, например, массы планет, а потом по этой модели с оптимальными параметрами находим так называемые наблюдаемые параметры орбит, то при аналитическом решение мы можем сразу решать уравнения находя эти параметры орбит, т.к. шесть элементов эллиптической орбиты (большая полуось, эксцентриситет, угол наклона, долгота восходящего узла, аргумент перигелия и средняя аномалия) точно так же как и три координаты в декартовой системе координат однозначно задают положение планеты в пространстве в любой момент времени. Кстати, аналитическим решением уравнений движения в оскулирующих элементах орбит объясняется то, что Ньюком в своих работах приводит не непосредственно, например, вековое смещение перигелия, а его произведение на эксцентриситет и не вековое смещение узла восхождения, а его произведение на синус угла наклона, т.е. в том виде как они входили в решаемые уравнения. 

 

 

 Таким образом, с введением в методику обработки данных наблюдений различных теорий, мы теперь, обрабатывая эти данные, получаем не экспериментальные параметры орбит, а экспериментально-теоретические, которые максимально соответствуют той теории, с помощью которой была построена математическая модель, параметры которой оптимизировались по данным наблюдений. Причем, если бы при этом не использовалась причинно-следственная связь, объединяющая по времени отдельные обороты планеты вокруг Солнца, то наличием этого промежуточного звена можно было бы пренебречь, т.к. по любой известной сейчас физической теории все планеты движутся по эллиптическим орбитам с небольшими колебаниями, вызванными воздействием других планет. И, следовательно, практически все теории для небольшого промежутка времени, например, для одного оборота планеты дадут примерно одинаковые параметры орбиты, имеющей форму эллипса.

 

 

Но дело в том, что эти эллипсы со временем немного смещаются в пространстве и, следовательно, со временем немного изменяются параметры орбит, например, аргумент перигелия или угол восхождения. Такое смещение обеспечивается причинно-следственной связью физических моделей. Эти незначительные изменения в параметрах орбит принято рассчитывать на промежутке в 100 лет и по этому они называются вековыми смещениями параметров орбит. И вот именно по этим вековым смещениям параметров орбит все последнее столетие определяется справедливость той или иной физической теории гравитации. Вернее не по самим смещениям, а по аномальным остаткам от этих смещений после вычета смещений, которые дает применение закона притяжения Ньютона, т.е. классическая механика. А самым известным и самым значительным сейчас считается аномальное смещение перигелия Меркурия. И ниже (в таблице 1) я привожу значения аномальных остатков смещения перигелиев четырех планет полученные Ньюкомом, которые не объясняются теорией Ньютона, но объясняются другими теориями в дополнение к смещению уже объясненному теорией Ньютона (в скобках указан источник, откуда взяты данные).

 

Таблица 1. Аномальное смещение перигелия внутренних планет.

 

	Меркурий	Венера	Земля	Марс
Наблюдения  (Ньюком [6])	575,06	42,52	1162,92	1602,69
теория Ньютона (Ньюком [6])	533,82	49,85	1156,95	1594,65
Аномальный остаток (Ньюком [6])	41,24	-7,33	5,97	8,04
теория Эйнштейна (Субботин [7])	43,0	8,6	3,8	1,4
теория Гербера (Хайдаров [8])	43,0	8,6	3,8	1,4
теория Ритца (Роузвер [9])	41,0	8,0	3,4	-
теория Маха (Зайцев [10])	43,0	23,0	17,0	11,0
теория Зеелингера (Роузвер [9])	41,3	7,3	4,2	6,3

 

 

 

Как видим, все эти теории хорошо объясняют аномальное смещение перигелия Меркурия и плохо объясняют эту аномалию для других планет. Из этого можно сделать вывод, что, либо все эти теории неадекватно описывают явления Природы, либо наблюдательные данные Ньюкома не верны, а может быть и то и другое. Какая из этих теорий (а может быть и какая то другая) окажется верной и поможет нам в дальнейшем по наблюдаемым величинам вековых смещений параметров орбит найти скорость распространения гравитации и абсолютную скорость Солнечной системы меня сейчас абсолютно не интересует и наша задача сейчас построить кинематическую теорию планет, чтобы самостоятельно найти эти вековые смещения параметров орбит планет. А для этих целей я буду использовать несколько модифицированную кинематическую методику Кеплера, т.е. буду аппроксимировать данные наблюдений эллиптическими орбитами планет.

 

 

Как мы видели в первой части этого цикла статей, применение современных теорий, полученных с использованием динамической методики, для древних затмений дает очень плачевные результаты. Сейчас эти ошибки объясняются тем, что Земля замедляет скорость вращения вокруг своей оси и по этому по современным теориям для заданного солнечного времени наблюдения (UT) получается, что Земля откручивается назад (для древних наблюдений) на угол меньше, чем надо. Следовательно, надо при заданной в теории угловой скорости вращения Земли отвернуть ее назад еще ну угол, который она сделает за время ET - UT, где ET это эфемеридное (равномерно текущее) время, которое используется или при аналитическом решение уравнений математической модели Солнечной системы (New0) или при численном, т.е. сейчас на компьютере (JPL2). Ведь один оборот вокруг своей оси Земля делает за 24 солнечных часа (UT) и сейчас и делала миллиард лет назад, но вот продолжительность этих часов, если  измерять продолжительность солнечного часа атомными часами, будет различной. Таким образом, и планеты вокруг Солнца и Луна вокруг Земли за один солнечный час (при их неизменной по атомным часам угловой скорости орбиты) повернутся в разное историческое время на разные углы, т.к. продолжительность солнечного часа будет разной. По этому, при расчете по современным физическим теориям нам надо обязательно учесть набежавшую разницу во времени, которая называется эфемеридной поправкой ET-UT, а при расчетах по теориям древних астрономов эта поправка не нужна, т.к. в кинематических теориях кругом используется солнечное время UT.

 

 

Для обработки как данных оптических наблюдений за планетами, так и данных, полученных по таблицам древних астрономов, в программе Solsys (начиная с 6-ой версии) я сделал еще одну форму №10. И на нижеприведенном рисунке Вы видите скриншот этой формы, где обрабатываются данные оптических наблюдений различных обсерваторий за Солнцем с 1924 по 1939 годы и где в наблюдательных данных учитываются поправки от нутации и планетной и звездной аберрации. Как я писал в первой части этого цикла статей, поправки от параллакса и рефракции в этих данных наблюдений уже учтены. Эти данные сравниваются с расчетными данными, т.е. с положением на эллипсе, параметры которого задаются или по упрощенной аналитической теории JPL0 (если включить переключатель JPL0) или по моей кинематической теории (Ser0 – на момент написания статьи теория уже создана и включена в 7-ю версию программы) или по плану (переключатель План), т.е. задаются произвольные параметры эллиптической орбиты на дополнительной форме №13. Только последовательность преобразования координат при внесение поправок я применил не стандартную, т.е. я наоборот в расчетные теоретические данные X1, Y1, Z1 вношу поправки, делающие их видимыми, а потом сравниваю с наблюдаемыми (видимыми) координатами X2, Y2, Z2.

 

 

 

 

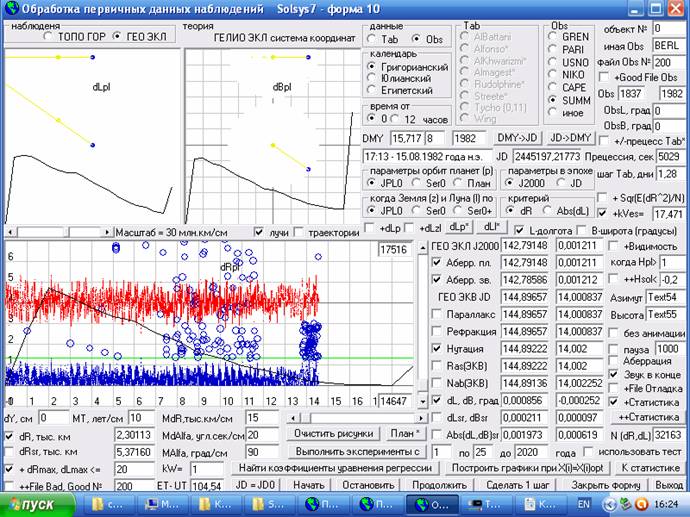
Рис.1 Скриншот формы №10 для обработки данных наблюдений различных обсерваторий и полученных из таблиц древних астрономов.

 

 

При этом на двух верхних рисунках выводятся расчетные данные положений Земли, Солнца и планеты (как кружки) в геоцентрической системе координат и в гелиоцентрической, а также в геоцентрической системе рисуется луч от Земли в направление, где должна находиться планета по наблюдаемым данным. А если обрабатываются данные оптических имитаторов, например, таблиц Птолемея или Аль Хорезми, то рисуется луч и в направление на Солнце. На нижнем рисунке выводятся все отклонения dR в тыс. км. наблюдаемого положения планеты от расчетного (как синие точки те, что меньше допустимого отклонения dRmax и как синие кружки те, значения которых больше dRmax и не идут в расчет среднего отклонения по всем наблюдениям dRsr) в масштабе MdR, а под рисунком в окошках выводятся все эти данные в численном виде. А в окошках справа от нижнего рисунка после вывода расчетных и наблюдаемых координат планеты выводятся  значения отклонений от расчетных положений наблюдаемых положений планеты по долготе L (в градусах) и широте B (в градусах).

 

 

А если после окончания обработки данных (если во время обработки был отмечен чекбокс Статистика) нажать кнопку Статистика, то на рисунках будут выведены и статистические распределения отклонений (черные ломаные кривые) по долготе dLpl в интервале от 0 до 17 угловых секунд, широте dBpl в интервале от 0 до 4,5 угловых секунд и по расстоянию dRpl от 0 до dRmax. При этом, масштаб количества точек в сантиметре задается в том же окошке, где и MdR (на рисунке было 250 точек в сантиметре и задается он непосредственно перед нажатием на кнопку Статистика), а самая последняя 18-я группа данных отражает количество наблюдений, не попавших в заданные интервалы, т.е. для dRpl это будет количество бракованных наблюдений, т.е. когда dRpl > dRmax. В данном случае у нас для типа данных выбран переключатель //Obs// (обсерватории), а название обсерватории выбрано //SUMM//, т.е. файл номер 150 с суммарными данными по нескольким обсерваториям. Программа позволяет получить кинематическую теорию как в фиксированной эпохе (переключатель //J2000//), так и в эпохе даты (переключатель //JD//), а также учесть некоторые периодические возмущения для планет от других планет, если отмечен чекбокс //+dLp// и для Земли и Луны если отмечен чекбокс //dLzl//, а на форме №22, где задаются периодические возмущения для планет (для Луны форма 21), можно задать по восемь возмущений от двух планет. 

 

 

А суть моей методики, вернее несколько модифицированной кинематической методики Кеплера, состоит в том, что, когда включен переключатель //План//, я произвольно задаю параметры орбит (на дополнительной форме №13) для одного прогона данных наблюдений (при проведение многофакторного планирования они изменяются в каждом прогоне (эксперименте) в соответствие с планом эксперимента), и во время всего прогона параметры остаются постоянные, кроме средней аномалии, которую я вычисляю для нужного мне момента времени по заданному начальному значению долготы и заданной угловой скорости. Время наблюдения я считываю из файла данных наблюдений или для таблиц задаю и по известным формулам, по заданным параметрам орбиты нахожу расчетные координаты планеты X1, Y1, Z1 в эклиптической гелиоцентрической, а потом в геоцентрической системах координат и определяю расчетное расстояние от Земли до планеты при таких параметрах эллипса и, если необходимо, перевожу данные из текущей эпохи в стандартную эпоху J2000. При этом координаты самой Земли я определяю сначала в гелиоцентрической системе координат для барицентра Земля-Луна, а потом, вычислив полярные координаты Луны, нахожу координаты уже самой Земли. Потом я вношу необходимые поправки в расчетные данные и получаю расчетные наблюдаемые геоцентрические координаты планеты в полярной системе координат. Затем, используя расчетное значение расстояния между Землей и планетой и координаты самой Земли, я нахожу реально наблюдавшиеся (видимые) геоцентрические координаты планеты X2, Y2, Z2 и определяю расстояние между расчетной и наблюдаемой точками dRpl, которое я использую в качестве критерия оптимизации при многофакторном планировании.

 

 

При этом, получающиеся отклонения наблюдаемых координат от расчетных  в одной и той же точке эллипса при разных оборотах планеты, которые вызваны, как притяжением от других планет, так и ошибками меридианных наблюдений, я считаю случайными величинами, которые распределены в соответствие с законом нормального распределения и, следовательно, при обработке данных наблюдений за несколько десятилетий, случайные отклонения взаимно уничтожаться и мы получим среднее отклонение координат расчетного эллипса от наблюдаемого. А вот отклонения наблюдаемых координат от расчетных, вызванные вековыми смещениями параметров орбит, являются уже не случайными величинами, и вековые смещения носят на небольших интервалах времени (до ста лет) линейный характер. По этому, после обработки данных наблюдений, например, с 1924 по 1939 годы (при условие, что данные распределены равномерно по годам) параметры расчетного эллипса будут относится к 1932 году.

 

 

Что касается вопросов самой оптимизации пяти параметров эллиптической орбиты - большая полуось, эксцентриситет, угол наклона, долгота восходящего узла и аргумент перигелия (а также начального положения планеты и ее угловой скорости), то здесь я применяю теорию многофакторного планирования, чтобы не подбирать параметры орбиты интуитивно, как это делал Кеплер. Но прежде чем немного пояснить суть многофакторного планирования я коротко остановлюсь на критериях оптимизации, т.к. ни у Ньюкома, ни у JPL по этому вопросу ничего не написано, а это важный момент. Оптимизацию параметров физической модели или кинематических элементов орбит можно производить по отклонениям расчетных значений от наблюдаемых по долготе и по широте для оптических наблюдений и по расстоянию до Земли для радарных наблюдений, но в таком случае оптимальные значения по одному критерию могут оказаться очень не оптимальными по другому критерию. А если использовать какой то комбинированный критерий, то все это будет очень субъективно, т.к. многокритериальные задачи объективно не решаются. Используя какой то один из показателей, например, отклонения по долготе или широте мы получаем, например, при наблюдении за Венерой с Земли отклонение в 1 угловую секунду, когда Венера и Земля находятся на минимальном расстоянии и это даст одно отклонение между расчетным и наблюдаемым положениями Венеры по расстоянию между этими точками в тыс.км., а когда она находится на максимальном удаление от Земли, то 1 угловая секунда даст в несколько раз большее отклонение по расстоянию. По этому я и использую в качестве критерия именно расстояние между точками с координатами X1, Y1, Z1 и X2, Y2, Z2. Более того, это отклонение не только является правильным критерием оптимизации, но и является к тому же единым критерием оптимизации.

 

 

Многофакторное планирование [13, 14] отличается от однофакторного, когда в каждом новом эксперименте изменяется значение только одного параметра (фактора), тем, что в каждом новом эксперименте изменяются по определенному плану один или все параметры. А после обработки экспериментальных данных мы получаем уравнение регрессии (чаще всего квадратичную аппроксимацию), которое отражает влияние всех параметров на критерий оптимизации (целевую функцию). Если у нас однофакторный эксперимент, то мы получим для квадратичной аппроксимации такое уравнение

Y=k0+k1*X1+k2*X1^2 (1)

где Y – критерий оптимизации, который надо минимизировать или максимизировать, X1 – оптимизируемый параметр, а k0,k1 и k2 – коэффициенты, которые мы получаем методом наименьших квадратов при статистической обработке данных. А вот, если у нас будет 4-е параметра, то мы получим, используя многофакторное планирование, уравнение регрессии следующего вида

Y = k0 + k1*X1 + k2*X2 + k3*X3 + k4*X4 +

+ k5*X1*X2 + k6*X1*X3 + k7*X1*X4 + k8*X2*X3 + k9*X2*X4 + k10*X3*X4 +

+ k11*X1^2 + k12*X2^2 + k13*X3^2 + k14*X4^2 (2)

 

Принципиально это уравнение отличается от уравнения, полученного при однофакторном планирование, наличием смешанных коэффициентов k5 … k10, которые отражают смешанное влияние параметров на критерий оптимизации. Задавая значения параметров в каждом эксперименте по определенному плану, мы получаем минимальное количество экспериментов необходимое для получения зависимости (2). Для очень грубого описания поверхности отклика системы, т.е. получения уравнения (2) достаточно выполнить план один раз, а для  точного описания вблизи оптимума надо последовательно выполнить несколько планов, приближаясь к области оптимума и уменьшая интервалы варьирования параметров. Планы бывают разные и, например, в программе Solsys7 на форме №18 можно работать с пятью разными планами - ортогональным, рототабельным, униформрототабельным, композиционным Бокса и почти D-оптимальным Бокса. Отличаются они разным количеством уровней варьирования факторов, величиной звездного плеча и количеством нулевых точек, а в конечном итоге это влияет на то, как будет размазана информация по гиперсфере. А на форме №13, где задаются параметры плана эксперимента я предусмотрел только два вида планов ортогональный и рототабельный. Первый позволяет более тщательно оптимизировать параметры вблизи оптимума, а второй за счет большего звездного плеча позволяет быстрее прийти в область оптимума, но иногда, чаще всего когда интервалы варьирования заданы плохо, процесс оптимизации (при автоматической оптимизации) может пойти в «разнос» и области оптимума достичь не удается, т.к. мы будем только удаляться от оптимума. Лучше всего в таком случае увеличить интервалы варьирования или задать новые параметры вручную (после первого выполнения плана), но иногда помогает просто смена одного плана на другой.

 

Для получения уравнения (2) нам необходимо, например, по ортогональному плану выполнить 25 экспериментов (24 на поверхности гиперкуба и один в центре). У этого плана факторы варьируются только на 3-х уровнях (включая нулевой) и звездное плечо будет равно 1. Обычно в планах 0 – означает, что параметр берется на нулевом уровне, +1 – на нулевом уровне плюс интервал варьирования и -1 - на нулевом уровне минус интервал варьирования, а т.к. у нас звездное плечо равно 1 и уровней всего три, можно писать просто 0 + - и по этому ортогональный план для четырех факторов будет выглядеть следующим образом

1 + + + +

2 + + + -

3 + + - +

4 + + - -

5 + - + +

6 + - + -

7 + - - +

8 + - - -

Следующие 8 опытов повторяют первые 8. Только первый параметр принимает кругом значение -1.

17 + 0 0 0

18 – 0 0 0

19 0 + 0 0

20 0 – 0 0

21 0 0 + 0

22 0 0 – 0

23 0 0 0 +

24 0 0 0 –

25 0 0 0 0

 

После обработки данных натурных или вычислительных экспериментов мы после нажатия на кнопку //Найти коэффициенты уравнения регрессии// на форме 10 получим уравнение (2), которое, безбоязненно, если у нас получилась поверхность, не имеющая седловых точек, дифференцируем по X1, X2, X3, X4 и получаем 4-е алгебраических уравнения. Решая теперь систему этих уравнений, автоматически находим оптимальные значения параметров X1, X2, X3, X4 при которых наша целевая функция (критерий оптимизации) принимает минимальное или максимальное значение (для этого надо нажать на кнопку //Оптимизировать отмеченные параметры// на форме 13). В нашем случае нам нужно минимальное значение, т.к. оптимизацию мы ведем по минимальной разности координат X1, Y1, Z1 и X2, Y2, Z2, т.е. между координатами полученными по заданным в плане параметрам орбит и между наблюдаемыми координатами планет (данные таблиц и обсерваторий). Скриншот формы №13, где задаются значения параметров орбит на нулевых уровнях, а также их интервалы варьирования и получающиеся оптимальные значения параметров приведен ниже.

 

 

 

 

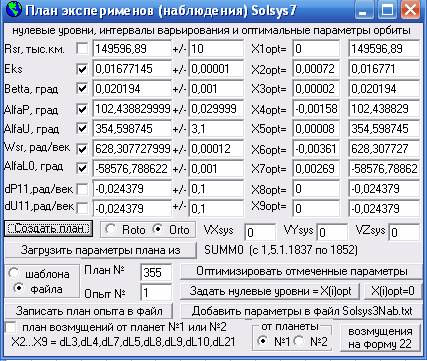
Рис.2 Скриншот формы №13 для работы с планами при обработке данных наблюдений.

 

Прежде чем перейти непосредственно к созданию кинематической теории планет хотелось бы особо остановиться на нескольких специфических моментах связанных с теорией многофакторного планирования. Первый из них связан с тем, что теория многофакторного планирования позволяет значительно снизить необходимое количество экспериментов, которые надо выполнить, чтобы получить квадратичное уравнение регрессии аналогичное уравнению (2). При этом априори принимается, что в исследуемой системе нет взаимодействий между факторами, влияющими на критерий оптимизации, выше парных, т.е. нет, например, взаимодействия X1*X2*X3 или X1*X2*X3*X4. По этому, приступая к исследованию какой то системы, желательно на тестовых примерах убедится, что в системе нет взаимодействий выше парных или их влияние на критерий оптимизации не велико.

 

Вторым специфическим моментом, связанным с теорией многофакторного планирования, является то, что оптимизацию ведут почти всегда по отклику системы (в нашем случае это будет по самим координатам планет, а не по отклонению расчетных координат от наблюдаемых). И до этого исследования, если не считать случая по оптимизации коэффициентов в формуле Планка, я оптимизировал параметры систем только по отклику системы, а не по разнице между откликом и каким-то заданным  значением. Сейчас же мы будем (см. формулу 3) вести оптимизацию по разнице между расчетными координатами, т.е. полученными при вычислительном эксперименте YRas(U) и наблюдаемыми координатами YNab(U) в каждом U-ом эксперименте плана. В дальнейшем этот критерий я буду называть dY в противовес критерию Y, который обычно применяется при многофакторном планировании, и где, при проведение натурных экспериментов, Yu0(U)= YNab(U), а, при проведение вычислительных экспериментов, Yu0(U)= YRas(U). Подробно о разнице в применение критериев dY и Y я расскажу в следующей части этого цикла статей, когда для оптимизации скорости гравитации нам потребуется еще более сложный критерий оптимизации чем (3), а сейчас просто констатирую, что применение критерия dY в наших исследованиях вполне допустимо.

Yu0(U) = (SUMMi Abs((YRas(U,i) - YNab(U,i))) / Ni                    (3)

Где: YRas(U,i) =R(X1(U,i),Y1(U,i),Z1(U,i)) – расчетные координаты i-го наблюдения

        YNab(U,i) =R(X2(U,i),Y2(U,i),Z2(U,i)) – наблюдаемые координаты i-го наблюдения

        i – номер наблюдения в выборке из Ni наблюдений

 

При этом задавая в каждом U-ом эксперименте плана разные параметры орбиты планеты мы можем зная расчетные и наблюдаемые координаты планеты в каждом i-ом наблюдении найти не только расстояние dR между этими двумя точками, но и dL - отклонение по долготе и dB – отклонение по широте. По этому при обработке данных наблюдений за Луной и Солнцем, когда можно считать, что они вращаются вокруг Земли мы можем частично использовать при оптимизации и критерий dL. Связано это с тем, что при наблюдениях за объектом вращающемся вокруг Земли при любом радиусе его орбиты отклонения по dR и по dL будут эквивалентны при незначительных отклонениях по dB. Кроме того, для оптимизации некоторых параметров орбит более точный результат будет по критерию dL, т.к. не будет погрешностей от ошибок в определение широты. Кроме того, существует много наблюдательных данных, где указывается только прямое восхождение, т.е. нельзя использовать критерий dR и по этому для орбит Луны и Земли я буду уточнять некоторые параметры и по критерию dL.

 

 

Необходимо также остановиться еще на одном аспекте многофакторного планирования. Непосредственно план многофакторного планирования обычно реализуется, когда параметры на нулевых уровнях находятся вблизи оптимума, а перед этим выполняется так называемое крутое восхождение в область оптимума. Делать это можно или наугад, что малоэффективно, или осуществляя покоординатное восхождение, когда в каждом новом эксперименте изменяется только один фактор, что достаточно утомительно, или с использованием линейных планов, что я считаю очень затратным, но менее эффективным, чем использование квадратичных планов. По этому, проводя вычислительные эксперименты на моделях систем, я всегда, вопреки рекомендациям учебников, использую только планы второго порядка. Объясняется это двумя причинами. Во-первых, число экспериментов, если мы не используем дробные реплики со смешанными коэффициентами (а дробные реплики отрицательно влияют на качество получаемой информации) при построение матрицы линейного плана для осуществления крутого восхождения, получается не на много меньше экспериментов, чем при планах второго порядка (для четырех факторов 16 вместо 24), что при проведение вычислительных экспериментов не на много увеличит время их проведения (материальных затрат при этом практически никаких). А, во-вторых, чтобы методом крутого восхождения достичь области близкой к оптимуму надо выполнить 3…5 планов первого порядка и при этом общее число экспериментов может быть даже больше чем в 2…3 планах второго порядка, т.к. информации от уравнения регрессии второго порядка можно получить гораздо больше и, следовательно, за меньшее число шагов достичь области оптимума.

 

А кроме этого, если мы используем планы второго порядка, как при поисковых экспериментах, так и при изучении поверхности отклика в области оптимума, то обработка данных производится по одной методике, что значительно упрощает код программы. Вот если бы эксперименты у нас были не вычислительные, т.е. не на математической модели, а натурные и нам в каждом эксперименте приходилось бы, например, запускать натуральную ракету к одной из планет, то тут можно было бы и подумать о различных градиентных методах для поиска области оптимума, т.к. после 2…3 планов экспериментов наши исследования, наверное, и закончились бы, т.к. просто кончились бы деньги, выделенные на эти исследования. В нашем же случае, т.к. персональный компьютер потребляет не много электроэнергии, приходится жалеть только о затраченном времени. И в заключение замечу, что я лично стараюсь получить всегда оптимум не просто в пределах интервала варьирования параметров, но и чтобы он получился вблизи нулевого уровня по каждому параметру и при разумных минимальных интервалах варьирования параметров.

 

 

Для создания кинематической теории планет я буду использовать не только наблюдательные данные различных обсерваторий за последние 200 лет, но и таблицы древних астрономов, которые отражают наблюдательные данные того времени. В качестве наблюдательных данных различных обсерваторий я использую в основном данные, выложенные на сайте Парижского бюро долгот. Эти данные меня привлекли тем, что для разных обсерваторий они там выложены в одном формате, что облегчает работу с ними. Причем в файлах с данными наблюдений, например, для Меркурия в разделе меридианных наблюдений http://www.bdl.fr/host/podb/podb2/int_merc_tr.html у них имеются два подраздела Original Date и Reduced Date. Но в файле из подраздела Original Date данные приведены в геоцентрической экваториальной системе координат, как прямое восхождение и склонение и для эфемеридного времени, т.е. минимальная обработка данных уже произведена. Кроме этого в данных уже учтена рефракция, что понятно, т.к. учесть ее позже, не зная погодных условий, при которых производились наблюдения, не возможно, а вот учтена ли суточная аберрация я так и не выяснил. Но зато я выяснил что время наблюдения в этих файлах все же указано не эфемеридное а всемирное (наверное просто опечатка). Данные из раздела Reduced Date я не стал использовать, т.к. во-первых нигде не указано какие изменения внесены в редуцированные данные, а во-вторых чтобы эти данные были совместимы с данными с других сайтов, где выложены не редуцированные данные.

 

 

 

А вот на сайте JPL (Лаборатория реактивного движения - подразделение НАСА) http://ssd.jpl.nasa.gov/plan-eph-data/index.html есть расшифровка формата их данных, из которой следует, что они могут быть опубликованы и в топоцентрической системе координат. Кстати, и Пулковская обсерватория публикует свои данные, как в топоцентрической, так и в геоцентрической системе координат, по этому, мне пришлось данные наблюдений, опубликованные не в геоцентрической экваториальной системе координат и в других форматах все приводить к формату Парижского бюро долгот (я его называю формат BDL). Кроме этого я данные наблюдений по одной планете различных обсерваторий буду записывать в один файл, который будет иметь название  SUMM, а в начале файла я буду давать информацию данные каких обсерваторий вошли в суммарный файл. Для этих целей я написал программу ObsData, которая позволяет не только прочитать данные в разных форматах и записать их потом в формате BDL, но и произвести с этими данными различные преобразования по времени и координатам, а затем скомпилировать их в одном файле. А моя программа Solsys позволяет сделать отбраковку данных наблюдений, как по отклонению в долготе, так и по отклонению в расстояние, т.к., как показало сравнение данных наблюдений с теорией JPL0 данные по многим наблюдениям являются или выполненными или записанными с явными ошибками. А, т.к., как мы видим на скриншоте программы (Рис. 1) распределение отклонений, как по долготе, так и по расстоянию не является строго нормальным я считаю не целесообразным производить отбраковку данных по среднеквадратичному отклонению и буду использовать отбраковку данных по среднему значению.

 

 

 

Но особенно много вопросов возникает при обработке данных древних астрономов, которые составляли свои таблицы при отсутствие каких-то официальных стандартов. К тому же и система счисления тогда использовалась шестидесятиричная и термины попадаются очень не понятные, и чтобы со всем этим разобраться надо окунаться в то время. Я вообще, когда занимаюсь каким ни будь вопросом (будь то астрономия или физика или экономика), всегда стараюсь ознакомиться не только с голыми формулами, которые остались после того или иного человека, но и проникнуться духом того времени, чтобы лучше понимать, что вкладывал тот или иной автор в свои формулы, которые нам достались. Хотя, если Вас интересует только суть вопроса, то, конечно же, лучше ознакомиться с современными комментариями по этому вопросу, чтобы быстро и без проблем понять, о чем идет речь. Но, если Вы собираетесь сами проанализировать ту или иную проблему и сделать свои выводы, то, конечно же, надо идти по пути углубленного изучения этой проблемы со всех сторон, а не только с математической стороны (тем более, в современной интерпретации).

 

 

Вот, например, возьмем Птолемея [1]. Он в то время отлично знал, что для мест наблюдения с разной долготой надо брать разное время для вычисления положений планет. Он даже ввел свой нулевой меридиан, который проходил где-то на Канарских островах (у Гиппарха нулевой меридиан был на острове Родос) и, например, долгота Рима у него была равна 36,7 градуса, а Александрии 60,5. Он также отлично знал, что Земля не только имеет форму шара, но и приблизительные ее размеры и по этому мог учесть в своих таблицах и параллакс (Аль Беруни (973-1050) знал эти размеры точнее и у него радиус Земли был 6403 км.). Ведь смог же он определить, что северный полярный круг, где наблюдаются полярный день и полярная ночь, находится за 70 параллелью. Более того, он уже в то время писал о рефракции (после публикации Альмагеста) и, наверное, мог бы как-то попытаться учесть и рефракцию в своих таблицах. Известно так же, что с рефракцией работал позже и Аль Хайам, но вроде бы первым, кто стал ее учитывать при астрономических наблюдениях был Вольтер (1430-1504), а потом уже появились известные таблицы рефракции Кеплера. Однако, когда обрабатываешь данные того или иного астронома древности никогда нельзя быть уверенным в том, какие поправки он учитывал при составление своих таблиц и вообще знал ли он об этих поправках.

 

 

Сейчас вообще существует мнение, что до Начал Ньютона даже никакие физические законы не были известны. А ведь уже в 15-м веке Леонардо да Винчи открыл 3-ий закон Ньютона, а также занимался теорией удара, оптикой, рассмотрел вопросы падения тел, законы движения тела, брошенного под углом к горизонту (доказал движение по параболе), рассмотрел движение тела по наклонной  плоскости – верно разложив и указав направление сил, введя силу давления и трения (верно поставил 5 вопросов зависимости сил трения, введя закон трения, и доказал зависимость от нагрузки и шероховатости, но неверно ввел коэффициент трения 0,25), создал теорию простейших механизмов: рычага, блока, наклонной плоскости, отрицал создание вечного двигателя, рассмотрел вопросы сложения сил, определения центра тяжести тел, сопротивления материала и т.д. и т.п.  Да что там 15-ый век. Уже в 13-м веке Роджер Бэкон вел не только астрономические наблюдения, но и проводил химические, оптические (упоминает о линзах, описывает очки) и физические опыты. А Пьер де Марикур впервые обстоятельно описывает свойства и методы применения магнита. Указывает, что магнит имеет полюса и как их найти, как намагнитить железную иглу.  По этому у меня будет просьба к читателям и в этой статье – если Вам известна дополнительная информация как об авторах таблиц, которые я перечислю ниже, так и о поправках, которые они учитывали, сообщите мне, пожалуйста.

 

 

А работал я со следующими таблицами (даю название, год издания, имя автора с указанием его времени жизни и место публикации или место, для которого эти таблицы составлены (не могу отличить), и, если стоит вопрос, то я не уверен в точности этой информации). Более подробная информация приводилась мною в первой части этого цикла статей [16].

 

Almagest – 132-147 год, Клавдий Птолемей (87-165?), Александрия

Handy – 500-700? годы, ничего не знаю об авторе, но это более поздняя версия таблиц Птолемея

AlKhwarizmi – 824? год, Мухаммад Ибн Мусса Аль Хорезми (780-850?), Багдад или Хорезм (сейчас это Ургенч в Узбекистане)

AlBattany – 910? год, Мухаммад Аль Баттани (858-929), Ракка или Баттани (Сирия)?

Toledan – 1080 год, Ибрагим Аз Заркали (1029-1087), Толедо (Испания – Кордовский халифат) – европейская копия таблиц Аль Баттани

Alfonso – 1252 год, коллектив авторов под руководством короля Кастилии Альфонса Х, Толедо (Испания).

Prutenic – 1551 год, Э. Рейнгольд (1511-1553), Берлин? – отпечатано в Тубингене (это первые гелиоцентрические таблицы после публикации в 1543 году Коперником своей теории, но выполненные также, как и таблицы Птолемея, с дифферентами и эпициклами).

Ticho – 1600 год, Тихо Браге (1546-1601), Ураниенборг (остров Вэн, около Копенгагена, Дания).
Rudolphino – 1627 год, Кеплер (1571-1630), обсерватория Т. Браге (Дания)

Streete – 1661 год, Стрит (1622-1689), Лондон

Wing – 1668 год, Винг (1619-1668?), Лондон

 

 

Как показала работа с таблицами, все они, кроме Прусских таблиц Рейнгольда, сделанных в спешке после выхода теории Коперника, вполне работоспособны. И хотя в таблицах Хэнди иногда возникают проблемы с таблицей хорд (наверное, когда тангенс близок к 90 градусам), но эти проблемы устранимы путем задания границы для не бракованных данных, например, учитывать при обработке только данные с отклонением до 300 тыс. км. А вот в Прусских таблицах проблемы гораздо более серьезные. Мало того, что угловая скорость не постоянна и ее колебания то увеличиваются, то уменьшаются, так еще периодически через 7 лет долгота изменяет свое значение мгновенно на значительную величину, что никак не позволяет получить стабильные данные, хоть на каком ни будь интервале времени. А вблизи 22 июня эти таблицы вообще выдают ошибку и мне пришлось программно исключить эти дни и для симметрии часть дней в декабре. Хотя есть, конечно, вероятность, что сам Рейнгольд не виноват, а виноват Robert Harry van Gent, с сайта которого http://www.phys.uu.nl/~vgent/astro/ancientephemerides.htm  я и скачал эти таблицы, оформленные им как таблицы Excel. А, т.к. я сам находил недоработки в его Excel таблицах, такой вариант вполне допустим. Но, учитывая то, что мне хватает проблем и без Прусских таблиц, разбираться, где там ошибка, я не буду и по этому в дальнейшем я просто не буду использовать эти таблицы (тем более, что для  1600 года много и других таблиц). И хотя все таблицы, кроме Прусских работоспособны, я в дальнейшем не буду использовать также таблицы Handy и Toledan, т.к. они являются просто копиями таблиц Almagest и AlBattany. Правда, последнее время, когда я стал работать на 64 битной версии Windows с таблицами AlKhwarizmi стали иногда возникать не понятные мне сбои, по этому будьте внимательны при работе с таблицами или работайте на 32 битных версиях Windows.

 

 

Теперь, когда мы разобрались с методами многофакторного планирования и с данными наблюдений, которые я буду использовать, возвращаемся опять к методике создания кинематической теории планет. Конкретно, с использованием методов многофакторного планирования, я оптимизировал такие параметры орбит планет как – величина большой полуоси эллипса R, его эксцентриситет Eks, угол наклона орбиты Betta, аргумент перигелия AlfaP, угол восходящего узла AlfaU, средняя начальная долгота AlfaL0 и угловая скорость обращения планеты Wsr. А для Луны я также оптимизировал скорости изменения аргумента перигелия dP11 и угла восходящего узла dU11, т.к. ввиду их значительного изменения за 20…30 лет их не возможно задать неизменными на этом интервале. При этом, значения AlfaP и AlfaU для Луны я также как и AlfaL0 оптимизировал на дату начала интервала времени JD0 (в юлианских датах) за который я оптимизировал данные. А ввиду того, что по геоцентрическим наблюдениям за Луной и Солнцем не возможно оптимизировать R для Луны и Земли, я для них этот параметр и не оптимизировал.

 

 

Итак, суть моей методики обработки данных наблюдений за планетами с целью получения кинематической теории планет, где параметры орбит очищены от влияния различных физических теорий, заключается в следующем. Т.к. все физические теории дают практически идеальную эллиптическую орбиту принимаем, что планета движется по эллипсу, а т.к. параметры этого эллипса изменяются на более-менее заметную величину (вековые изменения) только через 100 лет принимаем, что на интервале в 20…30 лет параметры орбиты остаются неизменными за исключением средней долготы, которую рассчитываем по формуле (4), где Wsr  задаем в радианах за 100 лет, а интервал времени dT от даты на которюу задано значение AlfaL0 в столетиях юлианских дат, т.е. dT=(JD - JD0) / 36525.

 

 

AlfaL = AlfaL0 + Wsr * dT   (4)

 

 

Теперь задаем значения параметров орбиты планеты по какой ни будь известной теории планет (у меня на форме 13 это JPL0) на дату JD0, задаем интервалы варьирования параметров от их значений на нулевых уровнях и создаем план по которому параметры орбит в каждом эксперименте будут изменять свои значения. Выбираем файл наблюдательных данных из которого будем считывать дату наблюдения и наблюдаемые координаты по долготе и широте (прямое восхождение и склонение) и указываем с кокой даты и по какую обрабатывать данные, а также задаем критерий для сравнения расчетных и наблюдаемых координат планет. Выполняем план эксперимента и после обработки полученных данных находим коэффициенты для уравнения (2).  Теперь по этому уравнению находим оптимальные параметры орбиты планеты для обработанных нами данных наблюдений. Таких опытов, где мы будем обрабатывать данные наблюдений за 20...30 лет у нас будет до 10, т.к. у нас имеются данные оптических наблюдений за планетами примерно за последние 200 лет. Для каждого опыта мы получим оптимальные параметры для даты примерно соответствующей середине интервала времени за который мы обрабатывали данные наблюдений. Все оптимальные значения для каждого опыта мы записываем в общий файл (надо после каждого опыта нажать на форме 13 кнопку //Добавить параметры в файл SolsysXNab.txt//, где X- номер планеты по которой мы обрабатывали данные наблюдений).

 

 

 

Теперь переходим к форме 6,  где мы можем произвести статистическую обработку полученных данных и найти по какой зависимости у нас изменяются со временем параметры

орбит. Загружаем данные из файла SolsysXNab.txt по нужному нам параметру орбиты и аппроксимируем экспериментальные данные одной из трех зависимостей

 

 

Alfa = k0                                         (5-1)

Alfa = k0  + k1 * dT                       (5-2)

Alfa = k0  + k1 * dT  + k2 * dT^2 (5-3)

 

 

 

 

 

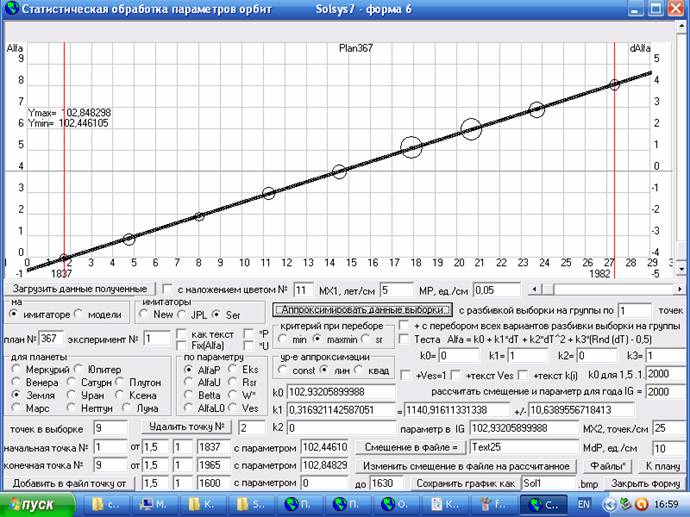
Рис.3. Скриншот формы 6 программы Solsys7 (статистическая обработка параметров орбиты Земли полученных по наблюдательным данным).

 

 

После обработки данных мы не только получим значения коэффициентов  k0, k1, k2 с доверительной вероятностью 95%, но и допустимые интервалы отклонения параметра Alfa при такой доверительной вероятности. Из трех зависимостей 5-1 ... 5-3 следует выбрать ту, где допустимый интервал, который берется равным двум среднеквадратичным отклонениям (sigma), будет минимальным. Например, на рисунке 3 у нас загружены данные по перигелию орбиты Земли, которые явно изменяются со временем и следовательно зависимость 5-1 нам точно не подходит. А вот определить на глаз изменяются ли эти параметры по линейной зависимости или по квадратичной иногда бывает сложно. По этому, обрабатываем данные и для зависимости 5-2 и для зависимости 5-3. У нас получается

 

 

AlfaP3 = 102,932059 + 0,316921  * dT    (+/- 10,6)

AlfaP3 =  102,929941 + 0,311234 *dT - 0,00315155 * dT^2   (+/- 10,8)

 

Здесь сам угол дан в градусах, а предельные отклонения в угловых секундах. Как мы видим дисперсия меньше у линейной зависимости, следовательно, для кинематической теории надо принять именно эту зависимость. Здесь уместно заметить, что даже если бы предельное отклонение 10,6 угл. сек получилось у квадратичной зависимости, а 10,8 у линейной, то при таком незначительном их отличие предпочтительнее выбирать линейную зависимость. Загружая и обрабатывая последовательно данные и по остальным параметрам орбиты Земли находим зависимости по которым они будут изменяться от заданной нами даты. У нас на форме 6 по умолчанию задано 1,5.01.2000, т.е. отсчет будет идти от эпохи J2000. А т.к. при обработке данных оптических наблюдений на форме 10 (рис.1) у нас был включен переключатель J2000, то и параметры орбит мы там получили в плоскости эклиптики эпохи J2000. А если бы был включен переключатель JD, то мы бы получили параметры орбит в текущей эклиптике, т.е. эпохе даты и обработав эти параметры на форме 6 мы бы тоже получили кинематическую теорию в эпохе даты. Но, как я неоднократно писал, сама теория планет является побочным эффектом моего исследования, т.к. основной моей целью является нахождение скорости гравитации по наблюдаемым смещениям параметров орбит и по этому меня в основном интересуют именно вековые смещения параметров орбит и обязательно в стандартной эпохе, т.к. при моделировании Cолнечной системы на форме 2 я буду получать параметры орбит в неподвижной эклиптике, т.е. в стандартной эпохе.

 

 

Прежде чем приступать к обработке данных оптических наблюдений необходимо в первую очередь посмотреть как согласуются между собою данные наблюдений различных обсерваторий а потом отбраковать из выборки те из них, которые резко отличаются от основной массы данных, чтобы, когда мы будем на форме 10 обрабатывать данные наблюдений, то бракованные данные не оказывали чрезмерное влияния на критерий оптимизации. В своей работе [4] (в переводе Вадима Чазова [5]) авторы пишут о их методике создания их модели Солнечной системы, т.е. о методике НАСА, разработанной в их подразделение JPL. В своей таблице 5.1 они указывают обсерватории, данные оптических наблюдений которых ими использовались, но далее пишут странную фразу //Все оптические наблюдения Солнца, Меркурия, Венеры и Марса были исключены из процесса улучшения модели DE405 по методу наименьших квадратов//. Отсюда не ясно то ли все данные оптических наблюдений были исключены, то ли только бракованные. А после того, как они приводят только список обсерваторий с данными радарных наблюдений, которые использовались для оптимизации параметров их модели, о данном документе вообще складывается очень противоречивое мнение и не понятно использовали ли они вообще данные оптических наблюдений.

 

 

 

Я для поиска параметров орбиты Земли отобрал самые многочисленные данные оптических наблюдений различных обсерваторий, т.е. те где имеется больше нескольких сотен наблюдений. Конкретно я объединил в один файл SUMM0_G_150.txt данные следующих обсерваторий PARI (1800-1906), GREN (1836-1954), USNO (1861-1982), CAPE (1907-1959), CAMB (1833-1869), HRST (1957-1977). Если мы сравним данные наблюдений с расчетными данными по теории JPL0 (см. рис.4), то мы увидим, что данные наблюдений по долготе отличаются от расчетных до 30 и более угловых секунд, но такие большие отклонения больше объясняются не ошибками наблюдательных данных, а наличием в них периодических возмущений от притяжения других планет, которые вызывают отклонение от идеальной эллиптической орбиты, рассчитанной по теории JPL0.

 

 

 

Рис.4. Сравнение наблюдательных данных за Солнцем по долготе с данными теории JPL0. Скриншот программы ObsData3.

 

 

Если в теории JPL0 учесть главные периодические возмущения от других планет (я взял около десятка поправок найденных Ньюкомом [11]), то мы уже будем иметь теорию JPL1 и она даст более менее приличный результат (см. рис.5).

 

 

 

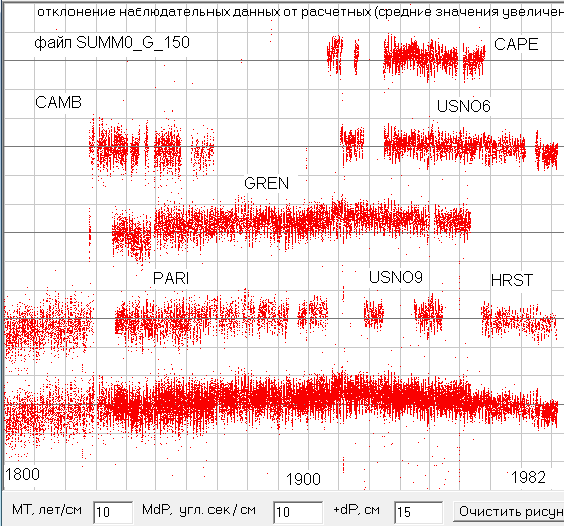
Рис.5. Сравнение наблюдательных данных за Солнцем по долготе с данными теории JPL1, т.е. JPL0 с главными поправками для периодических возмущений. Скриншот программы ObsData3.

 

И не смотря на наличие отклонений, доходящих до 10 угл.сек. и вызванных в основном не учтенными периодическими возмущениями, на рисунке уже явно видно, что отклонения в начале и в конце выборки отрицательные, а в середине положительные. Если мы выведем на этот же график отклонения всех обсерваторий по отдельности, то мы заметим, что отклонения обсерватории GREN почти все положительные, чего не должно быть, а обсерватории USNO6 (цифра это диаметр телескопа, т.к. их в обсерватории несколько телескопов) почти все более менее нормальные, а последняя серия наблюдений почему то резко ушла вниз. Все это явно говорит о том, что у всех обсерваторий имеются какие то свои специфические погрешности измерения, которые надо как то устранить. Кстати, о том, что данные Гринвичской обсерватории имеют ошибку около 4 секунд писал еще Ньюком, когда исследовал систематические погрешности приборов на различных обсерваториях. К сожалению по данным на рис.5 устранить эти погрешности очень сложно, т.к. имеется большой разброс отклонений, по этому я также сравнил эти данные наблюдений с расчетными данными JPL2, т.е. с эфемеридами DE405, в которых координаты рассчитываются с учетом всех периодических возмущений от планет (см. рис.6).

 

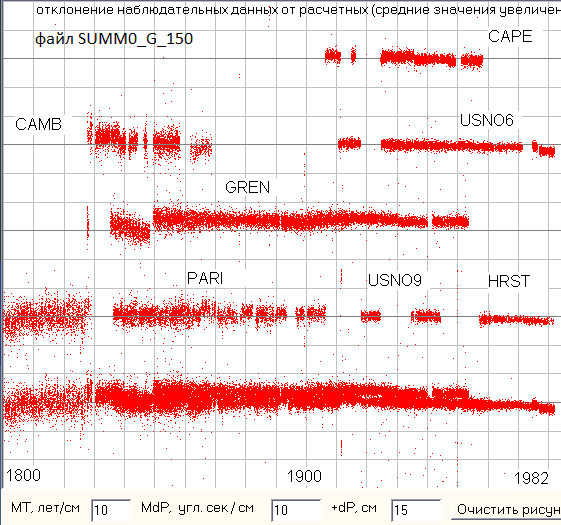
Рис.6. Сравнение наблюдательных данных за Солнцем по долготе с данными теории JPL2. Скриншот программы ObsData3.

 

Да,  картинка получилась более четкой, но все равно даже у самых хороших данных наблюдений имеются отклонения в несколько угловых секунд, хотя эфемериды DE405 рекламируются как дающие расхождение с наблюдаемыми данными в сотые или даже тысячные доли угл.сек. Как мы видим это совершенно не так и такая точность в этих эфемеридах может быть только при сравнение данных, рассчитанных при моделирование Солнечной системы, и описанием полученных расчетных данных в эфемеридах DE405 полиномами Чебышева, т.е. это точность аппроксимации расчетных данных. Но нам выбирать не приходиться, т.к. на сегодняшний день эфемериды DE405 считаются самой точной аппроксимацией именно наблюдаемых данных, т.е. де факто являются стандартом у астрономов. Дело иногда доходит даже до того, что вновь полученные данные наблюдений, отличающиеся от эфемерид DE405 бракуют. Мы конечно же не будем следовать этому правилу, а просто постараемся немного подравнять данные различных обсерваторий, т.е. отцентрировать их относительно данных JPL2. Такая центровка конечно же отразится на некоторых параметрах орбит, значения которых мы будем определять по этим данным, например, на AlfaL0 и AlfaU, но почти не должна сказаться на параметрах AlfaP и Eks, т.к. для их определения важно смещение данных по оси абсцисс, а не ординат.

 

Те данные, что можно исправить простым уменьшением или увеличением наблюдаемой долготы мы можем исправить используя программу ObsData, а вот, например, данные Гринвичской обсерватории с 1837 года по 1848 и Парижской с 1800 до 1829, где отклонение идет нарастающим итогом с помощью программы ObsData мы пока исправить не можем, по этому, мы их просто забракуем. Придется забраковать и данные Кембриджской обсерватории, т.к. их данные очень не стабильные и их использование тоже может не улучшить, а наоборот ухудшить полученные нами результаты. Кроме того, как видно на рис.6, данные Кембриджской обсерватории имеют очень большую ошибку и в определение широты Солнца, т.е. склонения.

 

 

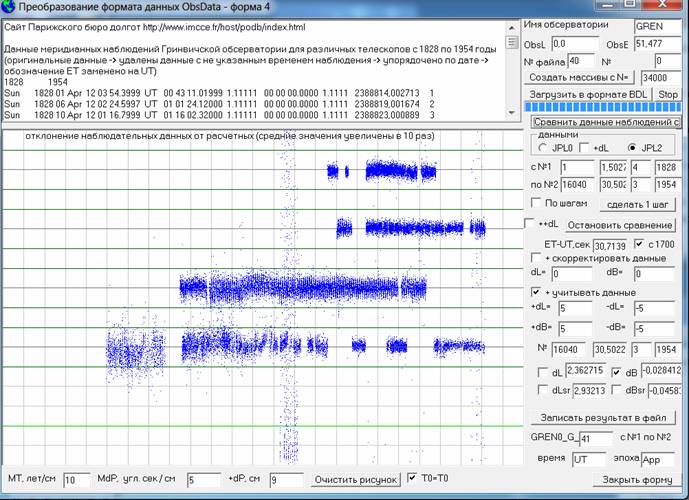
Рис.7. Сравнение наблюдательных данных за Солнцем по широте с данными теории JPL2. Скриншот программы ObsData3.

 

 

Аналогично данным наблюдений за Солнцем сравним с данными теории JPL2 и данные других планет и Луны (см. рис. 8...11). Как видим у всех планет есть данные, где долгота смещается относительно теоретических данных или вверх или вниз, а у Луны мы видим отклонения и по широте. И хотя у некоторых обсерваторий явно просматривается отклонение по всем планетами в одну сторону, но для одних планет оно имеет одну величину, а для других другую величину, что говорит о том, что имеются не только систематические погрешности в наблюдательных данных этих обсерваторий, но и ошибки в определение расчетных координат у теории JPL2. Таким образом, примененная мною центровка данных относительно данных теории JPL2 это не идеальный вариант, но другого простого способа отцентровать данные я пока не вижу. По этому, там где данные смещены относительно центра, за который мы принимаем расчетные данные теории JPL2, на заметную величину мы их подкорректируем так, чтобы смещение относительно центра пропало. Причем будем изменять долготу, а для Луны и широту, на заданном интервале времени на одну величину для всех наблюдений. Значения этих интервалов и смещений даны в таблице 2. А затем мы скомпилируем из отцентрованных данных новые файлы данных оптических наблюдений за планетам SUMM0_G_200, SUMM1_G_200, SUMM2_G_200, SUMM4_G_200, SUMM11_G_300, где цифра после SUMM это номер планеты (0 - Солнце, 11 - Луна).

 

 

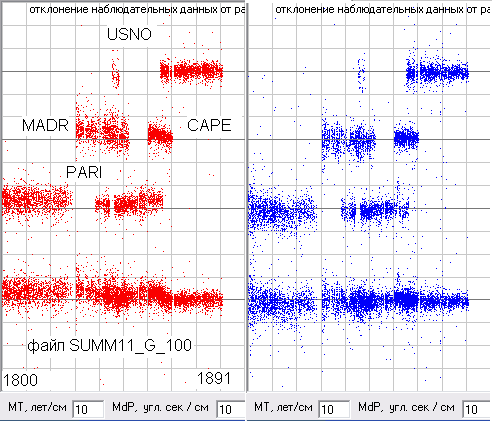
Рис.8. Сравнение данных наблюдений за Луной по долготе (красные точки) и по широте (синие точки) с данными теории JPL2. Скриншот программы ObsData3.

 

 

 

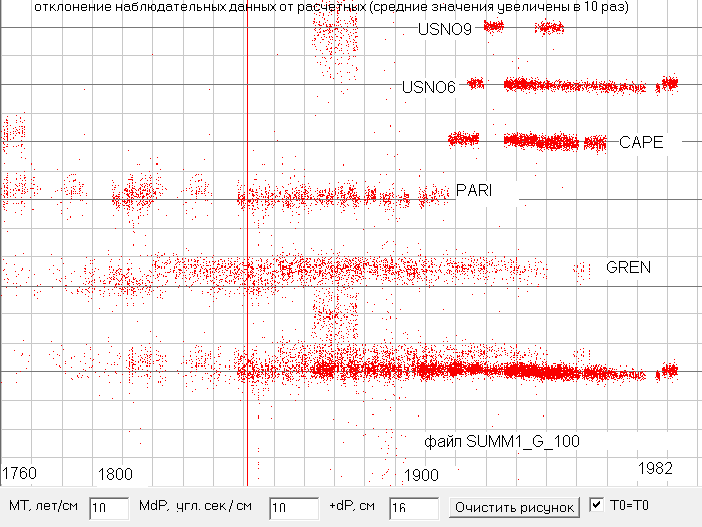
Рис.9. Сравнение данных наблюдений за  Меркурием по долготе с данными теории JPL2. Скриншот программы ObsData3.

 

 

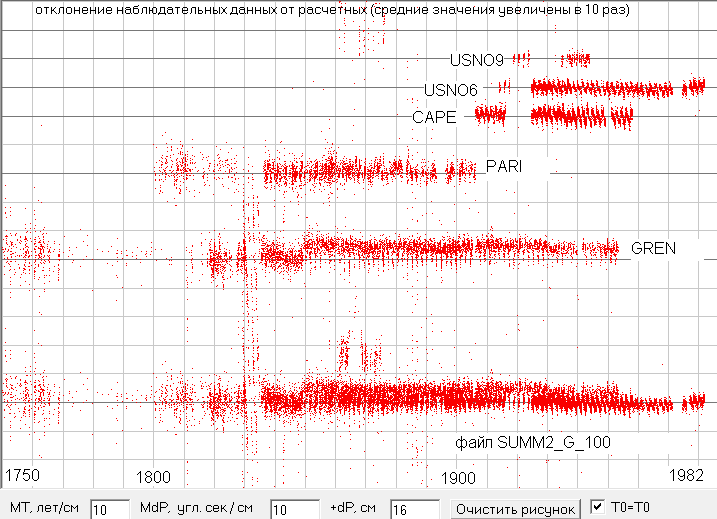
Рис.10. Сравнение данных наблюдений за Венерой по долготе с данными теории JPL2. Скриншот программы ObsData3.

 

 

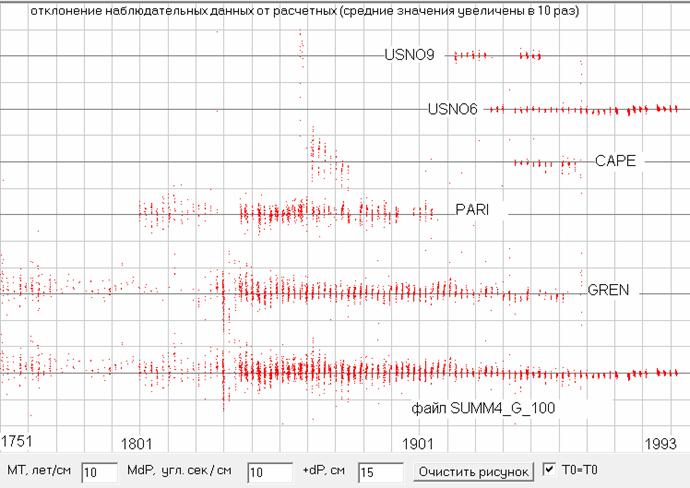
Рис.11. Сравнение данных наблюдений за Марсом по долготе с данными теории JPL2. Скриншот программы ObsData3.

 

Таблица 2. Принятые поправки к наблюдаемым координатам при их центровке по теории JPL2.

 

	Солнце	Луна dL	Луна dB	Меркурий	Венера	Марс
PARI 1800-1828 PARI 1829-1837 PARI 1838-1866 PARI 1866-1906 PARI 1907-1924	-     - -0,75 -0,75 -	-2,62 - -2,62 - -	+1,15 - +1,15 - -	- -0,7 -0,7 -0,7 -0,7	-0,73 -0,73 -0,73 -0,73 -	-0,59 -0,59 -0,59 -0,59 -
GREN 1751-1828 GREN 1828-1848 GREN 1849-1954	- - -3,6	- - -	- - -	- - -5,72	- - -3,62	-2,19 -0,51 -0,51
CAPE 1861-1870 CAPE 1907-1916 CAPE 1925-1936 CAPE 1936-1958	- -1,06 -0,7 +0,42	-1,66 - - -	-0,67 - - -	- -0,68 -0,68 +0,33	- 0 0 0	- - - +0,8
USNO6 1867-1891 USNO6 1911-1932 USNO6 1933-1956 USNO6 1957-1976 USNO6 1976-1982 USNO6 1983-1993	- 0 0 +0,8 +2,73 -	0 - - - - -	+0,79 - - - - -	- 0 +0,65 +0,65 -0,48 -	- 0 0 0 0 -	- - 0 0 0 0
USNO9 1916-1946	0	-	-	0	0	0
HRST 1957-1982	+1,1	-	-	-	-	-
MADR 1831-1852	-	-3,0	+0,51	-	-	-

 

 

Таблица 3. Количество оптических наблюдений и интервалы наблюдений различных обсерваторий использованные в расчетах.

 

	Солнце	Луна	Меркурий	Венера	Марс
интервал	1837-1982	1800-1891	1837-1982	1800-1982	1751-1993
к-во наблюдений	36405	7824	8310	19147	5775
к-во dL	35160	7495	8105	18626	5626
к-во dR	33110	6764	7795	17903	5411
PARI	1837-1906	1800-1866	1837-1906	1800-1906	1800-1905
GREN	1849-1954	-	1850-1953	1850-1954	1751-1954
CAPE	1907-1959	1861-1870	1907-1959	1907-1958	1935-1958
USNO6	1911-1982	1866-1891	1913-1982	1914-1982	1926-1993
USNO9	1918-1944	-	1918-1944	1919-1944	1913-1944
HRST	1957-1982	-	-	-	-
MADR	-	1831-1852	-	-	-

 

 

Но прежде чем приступать к оптимизации параметров орбит по отцентрованным нами данным наблюдений надо еще произвести отбраковку из этих файлов тех наблюдений, которые являются явно ошибочными, когда отклонение от расчетных данных составляет больше десятков угл.сек., а часто и градусов. Для этого воспользуемся программой Solsys и зададим, как это видно на рис.1 предельное допустимое отклонение в окошке //dRmax, dLmax <=// для выбранного критерия оптимизации dR или Abs(dL), а в окошке у чекбокса //++FileBad, Good №//, который отметим, зададим номер файла для записи отбракованных данных. И на рис.1, где задана отбраковка по dR, т.е. по расстоянию, Вы видите малую часть таких данных, которые в отличие от хороших данных изображаются не точками, а кружками. При этом отбраковку мы будем производить по теории JPL0, т.е. без учета периодических возмущений, и по этому хорошими будем считать по критерию Abs(dL), т.е. по абсолютному значению отклонения в долготе, те, которые отклоняются менее чем на +/-22 угл. секунды. В результате мы получим файл с расширением на конце L, т.е. для данных наблюдений за Солнцем получим файл  SUMM0_G_200L. И на рис.12 Вы видите отклонения наблюдательных данных в этом файле от теории JPL0. Теперь этот файл можно разбить на опыты, т.е. интервалы по 20...30 лет и производить оптимизацию параметров орбит, но только по критерию Abs(dL), по этому сделаем еще и отбраковку данных по критерию dR, задав максимально допустимое отклонение по расстоянию +/-12 тыс.км. У нас получится файл SUMM0_G_200LB.

 

Рис. 12.  Отклонения наблюдательных данных в файле  SUMM0_G_200L по долготе от теории JPL0. Скриншот программы Solsys7.

 

В отличие от данных в файле SUMM0_G_150 (см. рис. 4, 5, 6) у нас пропала нелинейность отклонения данных от центра, т.е. от данных теории JPL0, но сами отклонения остались такие же большие как на рис.4. И хотя, как я писал выше, наличие периодических возмущений не является препятствием для применения моей методики обработки наблюдательны данных, но я боюсь, что полученные при этом огромные допустимые отклонения обесценят полученные смещения параметров орбит. По этому, я произведу поиск параметров орбит как без учета поправок от возмущений планет, так и с частичным учетом этих поправок. Вот только поправки найденные Ньюкомом, которые мы использовали в программе ObsData3 (см. рис.5), я применять не хочу, т.к. опасаюсь, что они могут убрать и отклонения (возмущения), которые нам нужны для нахождения оптимальных параметров орбит. Дело в том, что при различных эксцентриситетах эллипса и разных положениях перигелия у нас будут наблюдаться различные отклонения от какой то эталонной орбиты. И происходить эти отклонения будут с периодом равным периоду обращения исследуемой планеты. По этому, если в используемых нами поправках для учета периодических возмущений будут такие, период которых будет близок к периоду обращения исследуемой планеты, то эффект от эксцентриситета и перигелия может быть или искажен или исключен полностью и мы не сможем производить оптимизацию этих параметров орбит. А при поиске периодических возмущений Ньюком использовал ряды Фурье для которых важна только логика математической целесообразности и по этому в его поправках могут найтись и такие, где период совпадет с периодом обращения исследуемой планеты.

 

По этому, я принял решение найти самому часть поправок для периодических возмущений используя стандартную логику, т.е. логику Аристотеля. И за основу я решил взять формулы восьми основных поправок из теории Брауна для Луны. Все эти поправки учитывают влияние Солнца (кроме 2-х первых) на орбиту Луны, но аналогичное влияние должны оказывать на орбиты планет и другие планеты. Формулы и значения коэффициентов в основных поправках Брауна приведены на рис.13. При этом учитывать я буду только те поправки, которые влияют на долготу планеты  (возмущения в широте планет очень маленькие) и не все, а только те, которые оказались нужными и  значимыми для эллиптической орбиты Луны. Дело в том, что Браун создавал свою теорию Луны приняв, что она движется по окружности, т.е. так как это было и у Птолемея и у Тихо Браге. Мы же будем находить поправки для эллиптической орбиты Луны и по этому поправки от 1-го и 2-го главных неравенств, которые учитывают влияние эллиптичности орбиты Луны нам не нужны. Причем, то, что Браун и древние астрономы использовали круговую орбиту Луны не обесценивает все найденные ими поправки и с таким же успехом можно было взять за основу и шестигранную орбиту Луны и находить поправки для нее. Самое главное, что найденные ими поправки получены ими с применением стандартной логики, когда влияние той или иной поправки имеет логическое объяснение, т.е. в периодах изменения этих поправок имеется логика.

 

 

Рис. 13. Скриншот формы 21, где можно задать значения основных возмущений в орбите Луны от влияния на нее притяжения Солнцем.

 

Для Луны я значения всех этих поправок не находил, а принял их такими как они даны в теории Луны Брауна (только не использовал некоторые из них, которые не подходят для эллиптической орбиты Луны). Связано это с тем, что теория Луны нужна мне только для того, чтобы по координатам барицентра Земля-Луна найти потом, зная геоцентрические координаты Луны, гелиоцентрические координаты именно Земли с которой велись наблюдения за планетами и Солнцем. А создавая теорию Земли мы, как и все остальные астрономы, будем для движения барицентра Земля-Луна. И хотя для этих целей подошла бы и любая уже известная теория Луны я все же много внимания уделил и теории Луны, т.к. многие формулы для возмущений здесь найдены с использованием стандартной логики. Например, формулы для 1-го и 2-го главных неравенств и эвекции найдены Птолемеем, а для вариации и годичного неравенства Тихо Браге. По этому, я взял из теории Луны Брауна восемь формул по которым находил значения коэффициентов, отражающих влияние на орбиту планет притяжения двух других планет. Можно, конечно же было бы найти и побольше поправок и от большего количества планет, но для меня сейчас важно проверить не помешает ли учет периодических возмущений в поиске оптимальных параметров орбит планет.

 

Поиск коэффициентов для возмущений я производил по той же методике, что разработал для поиска оптимальных параметров орбит. Только на форме 13 я задавал не параметры орбит на нулевых уровнях и интервалы их варьирования, а коэффициенты для формул возмущений и интервалы их варьирования. Для этого надо на форме 13 (см.рис.2) отметить чекбокс //план возмущений от планет №1 или №2   X2...X9 = dL3, dL4, dL7, dL5, dL8, dL9, dL10, dL21// и выбрать номер планеты периодические возмущения от которой мы будем оптимизировать. При этом параметры орбиты будут определяться по существующим теориям планет (надо выбрать на форме 10). После того, как оптимальные коэффициенты возмущений будут найдены их следует отправить на форму 22, где они будут записаны в файл, а при загрузке формы будут считаны из файла и потом их можно использовать как для существующих теорий, так и для оптимизируемых параметров орбит, которые мы задаем по плану эксперимента. Все найденные мною коэффициенты для расчета возмущений четырех планет от двух других планет, которые прибавляются к расчетным координатам планет представлены на рис.14. А для того, чтобы при обработке данных наблюдений на форме 10 учесть эти возмущения надо отметить чекбоксы //dLp// для Меркурия, Венеры и Марса и  //dLzl// для Земли и Луны.

 

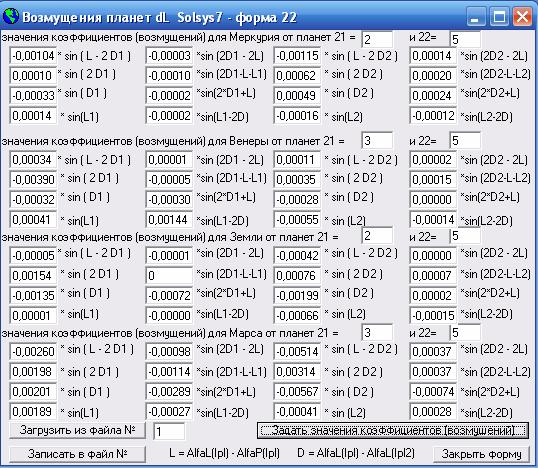
Рис.14. Значения коэффициентов в формулах возмущений для 4-х планет от воздействия на них 2-х других планет. Скриншот программы Solsys7.

 

Результат сравнения наблюдаемых данных из файла SUMM0_G_200L с теорией JPL0 с учетом периодических возмущений в орбите Земли, т.е. с теорией JPL1, представлен на рис. 15, где явно видно, что с применением периодических возмущений отклонения наблюдаемых данных от расчетных уменьшились в 2 раза. Но теперь мы также видим, что в файле SUMM0_G_200L осталась часть явно бракованных наблюдений, которые ввиду большого отклонения от расчетных данных могут оказать заметное влияние на ошибку в определение оптимальных параметров орбиты Земли. По этому, мы делаем еще два файла отбракованных данных SUMM0_G_201L и SUMM0_G_201LB, где данные из файла SUMM0_G_200 отбраковываем по теории  JPL1 и задаем допустимые отклонения наблюдаемых данных от расчетных соответственно +/-10 угл.сек. и +/-5 тыс.км.

 

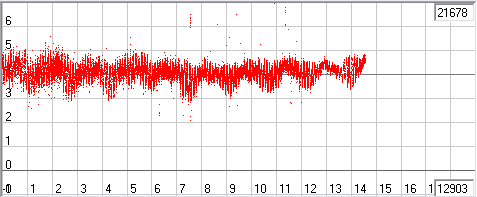
Рис. 15.  Отклонения наблюдательных данных в файле  SUMM0_G_200L по долготе от теории JPL1. Скриншот программы Solsys7.

 

Более того, теперь мы видим, что в отклонениях по долготе просматривается какая то цикличность с периодом около 16 лет, т.е. какие то заметные периодические возмущения мы явно не учли. По этому я решил разбить всю выборку на опыты кратные 16 годам, чтобы эта цикличность не повлияла на результаты оптимизации. Конкретно я решил разбить данные на 16, 32 и 48 лет и посмотреть, как продолжительность опытов влияет на точность получаемых данных. У меня получились следующие интервалы для 3, 5 и 9 опытов, где после указания интервала я даю количество наблюдений в этом интервале по критерию dR, т.е. когда в файле приведены данные и по долготе и по широте для этих наблюдений.

 

Таблица 4. Интервалы опытов для обработки данных наблюдений за Солнцем.

1	1837-1884 / 6467	1837-1868 / 4275	1837-1852 / 1667
2	1885-1932 / 11705	1869-1900 / 5031	1853-1868 / 2608
3	1933-1980 / 11992	1901-1932 / 8866	1869-1884 / 2192
4		1933-1964 / 10076	1885-1900 / 2839
5		1965-1980 / 1916	1901-1916 / 3610
6			1917-1932 / 5256
7			1933-1948 / 6286
8			1949-1964 / 3790
9			1965-1980 / 1916

 

 

Теперь открываем на форме 10 нужный нам для работы файл наблюдений указав его номер 200 и выбрав критерий оптимизации dR или Abs(dL), чтобы программа знала с каким окончанием L или LB файл  SUMM0_G_200 загрузить. Выбираем в рамочке //параметры орбит планет (р)// переключатель //План// и задаем в соответствующих окошках дату с которой мы будем обрабатывать из файла данные и год до которого мы (включительно) будем их обрабатывать. Теперь переходим к форме 13, где нам надо задать параметры орбиты на нулевых уровнях и интервалы их варьирования. Если мы уже предварительно работали с этим опытом, то мы загружаем эти данные из файла, а если нет, то выбираем переключатель //шаблон// и загружаем параметры орбиты которые рассчитываются по теории JPL0 на дату которую мы указали на форме 10. Вместе с параметрами на нулевых уровнях загрузятся и какие то начальные интервалы варьирования, которые после выполнения первого прикидочного плана Вы сможете изменить так, чтобы влияние всех параметров на критерий оптимизации было примерно одинаково. Это вы увидите на форме 10 после построения графиков влияния каждого параметра на критерий оптимизации по полученному Вами уравнению регрессии (2), когда для каждого графика все параметры кроме одного задаются равными оптимальным значениям (см. их значения на форме 13).

 

Теперь отмечаем те параметры, которые мы будем оптимизировать, выбираем тип плана (ортогональный или рототабельный) и жмем на кнопку //Создать план//. Возвращаемся к форме 10 и нажимаем кнопку //Выполнить эксперименты с// (в окошке должен быть номер 1) и по (в окошке после создания плана появляется номер последнего эксперимента в этом плане). После выполнения плана нажимаем на кнопку //Найти коэффициенты уравнения регрессии//. Затем полезно будет нажать на кнопку //Построить графики при X(i)=X(i)opt//, чтобы визуально оценить влияние каждого параметра орбиты при заданном для него интервале варьирования на критерий оптимизации. И на рис.16 Вы видите такое влияние 5-и факторов на критерий оптимизации (параболы) и две колонки цифр, которые являются критерием оптимизации при выполнение экспериментов по плану (левая колонка) и критерием рассчитанным по полученному уравнению (2) правая колонка. При этом Вы видите только часть критериев в экспериментах (последние номера), а на рисунке выводится и много другой информации, например, коэффициенты уравнения (2), план эксперимента, решение системы линейных уравнений и т.д. И, чтобы посмотреть всю информацию надо прокрутить рисунок по вертикали и горизонтали. Значения наблюдаемых и расчетных значений критерия оптимизации выводятся на рисунок и в графическом виде (маленькие кружки – экспериментальные значения, а большие – расчетные) и для удовлетворительной точности при оптимизации надо задавать интервалы варьирования параметров такие, чтобы маленькие кружки были внутри больших или хотя бы касались их с наружной стороны.

 

Рис. 16. Влияние каждого фактора по отдельности на критерий оптимизации при изменение его значения от -1 интервал до нулевого уровня и потом до +1 интервал при неизменных значениях остальных факторов (задаются их оптимальные значения с формы 13).  Скриншот программы Solsys7.

 

 

Теперь, наконец то, нажимаем на форме 13 кнопку //Оптимизировать отмеченные параметры// и в соответствующих окошках увидим какие у нас получились оптимальные параметры орбиты (в закодированном и раскодированном виде). Теперь нажимаем на кнопку //Добавить параметры в файл Solsys3Nab.txt// и у нас полученные параметры орбиты для этого опыта записываются в файл, где у нас будут записаны оптимальные параметры и для всех остальных опытов. При этом не только оптимальные параметры, но и уровни варьирования, дата начала опыта и год окончания, а также другие данные можно записать в отдельный файл (надо на форме 13 нажать кнопку //Записать план опыта в файл//). Затем эти данные можно загрузить и произвести оптимизацию по другому критерию или при обработке данных из другого файла. После того, как будут выполнены все опыты, переходим на форму статистической обработки данных, загружаем данные по выбранному параметру (они выводятся на график как отдельные точки для каждого опыта в заданном масштабе) и жмем кнопку //Аппроксимировать данные выборки//. Получаем уравнение, которое описывает как должен со временем изменяться данный параметр орбиты, чтобы отклонение наблюдаемых данных от расчетных было минимальным. После того, как мы получим уравнения по изменению всех параметров у нас будет так называемая теория данной планеты. А после того, как мы получим такие уравнения по всем планетам, у нас будет кинематическая теория планет, которая по своему виду ничем не будет отличаться от аналогичной  теории Ньюкома или теории JPL.

 

Вот только оптимизация параметров орбит будет не такой быстрой, как я написал выше и Вам придется выполнять десятки планов по оптимизации параметров орбиты только для одного опыта. Во-первых, Вы сразу не зададите правильно интервалы варьирования и будете их уточнять после выполнения очередного плана. Во-вторых, параметры заданные на нулевых уровнях по теории JPL0 будут не оптимальными для данного опыта и Вам придется выполнить несколько планов, чтобы только приблизиться к области оптимума. Затем, для более точного описания гиперсферы вблизи области оптимума Вам надо будет уменьшить интервалы варьирования параметров и опять выполнить несколько планов пока Вы не увидите, что дальнейшего приближения к оптимуму не происходит или Вы добились нужной Вам точности. Обычно я произвожу оптимизацию до тех пор пока точность найденных параметров будет не более одной сотой (в закодированном виде) от интервала варьирования параметров. Но абсолютная точность зависит также от величины самого интервала варьирования параметров (факторов). Более того, там, где надо оптимизировать 7 параметров (для планет, кроме Земли) или 8 для Луны, каждый план придется разбивать на два плана, т.к. в программе Solsys7 предусмотрено выполнение максимум шестифакторных планов.

 

Вообще то я рекомендую и 6-и факторные планы разбивать на два, например, 3 и 3 или 4 и 2, т.к. при 6-и факторном ортогональном плане надо выполнить 77 экспериментов, а при 2-х трехфакторных планах только 30 экспериментов. При этом мы сначала выполняем трехфакторный план по первым 3-м параметрам (при неизменных 3-х вторых), затем по вторым, потом опять по первым, а потом опять по вторым и т.д. При этом, разбивка одного большого плана на два маленьких полезна для точности оптимизации, т.к. чем больше факторов, тем больше появляется взаимодействий выше парных. А, как я писал, получаемое нами уравнение регрессии (2) отражает только парные взаимодействия и, по этому, чем меньше факторов в плане, тем меньше взаимодействий выше парных и тем точнее получается  уравнение регрессии (2). Но, когда на форме 13 мы нажимаем на кнопку //Записать план опыта в файл//, мы записываем все параметры необходимые для проведения 9-и факторного эксперимента в папку с номером этого плана, как файл с номером опыта, а коэффициенты уравнения регрессии (2) записываются только для последнего выполненного конкретного плана, например, 4-х или 3-х факторного. А вообще, для оптимизации таких параметров как AlfaL0 и Wsr желательно всегда выполнять 2-х факторный подплан, т.к. между этими двумя факторами очень сильная функциональная связь. А остальные факторы (параметры) можете оптимизировать как одним подпланом, так и дальше разбивать на несколько подпланов.

 

Но все эти подробности и тонкости работы с программой Solsys7 Вы найдете в описание к программе, когда я ее выложу на своем сайте (пока выложена 6-я версия), а сейчас давайте вернемся к создаваемой мною кинематической теории планет и получающимся при этом вековым смещениям параметров орбит. В таблице 5 Вы видите вековые смещения оптимальных параметров орбиты Земли, которые у меня получились при разном количестве опытов, разных критериях, при учете или не учете периодических возмущений и при обработке данных разных файлов. Первое, что бросается в глаза это уменьшение доверительных интервалов для найденных оптимальных параметров орбит при учете периодических возмущений при получающихся примерно одинаковых значениях вековых смещений этих параметров (при линейной аппроксимации параметров орбит). Сравните аналогичные планы 351...357 и 361...367. Причем обращаю ваше внимание, что здесь и далее предельные отклонения даются так как они получаются на форме 6, т.е. именно для параметров орбит, а не для вековых смещений. И, если предельное отклонение для параметра на промежутке в 150 лет получается 30 угл.сек., то для векового смещения, т.е. за 100 лет, оно будет 20 угл.сек. Учитывая положительное влияние учета периодических возмущений на точность оптимизации параметров орбит в дальнейшем при оптимизации параметров орбит Луны, Меркурия, Венеры и Марса я буду выполнять только эксперименты, где периодические возмущения учитываются.

 

Таблица 5. Вековые смещения параметров орбиты Земли, полученные на программе Solsys7 при обработке данных оптических наблюдений за Солнцем. При выполнение планов 351…357 использовались файлы 200L и 200LB, где отбраковка данных из файла SUMM0_G_200 шла по теории JPL0 без учета периодических возмущений, а при выполнение планов 361...367, 3611…3671 и 386, 387 использовались файлы 201L и 201LB, где отбраковка данных шла с учетом периодических возмущений или по теории JPL0 для 361...367 или по предварительной теории Ser00 полученной по данным планов  361…367 (3, 5 и 9 количество опытов на которое разбивалась вся выборка, L и R критерии оптимизации, а +dL и -dL означает учитывались или нет периодические возмущения).

планы	dAlfaP	dAlfaU*	dBetta	dEks	dWsr
351= 5R   -dL	1120,2+/-61,6	-868,0+/-23,9	-47,17+/-0,25	-42,27+/-4,02	24+/-34
353= 5L   -dL	1126,2+/-67,5	-	-	-41,38+/-4,44	6+/-44
355= 9R   -dL	1148,1+/-67,1	-868,0+/-23,9	-47,54+/-0,23	-41,89+/-4,13	-16+/-75
357= 9L   -dL	1146,0+/-73,7	-	-	-41,18+/-5,44	6+/-110
361= 5R +dL	1140,4+/-10,3	-868,0+/-23,9	-47,27+/-0,45	-42,42+/-0,38	-31+/-12
363= 5L +dL	1136,6+/-11,6	-	-	-41,56+/-0,90	-47+/-8
365= 9R +dL	1143,5+/-13,2	-868,0+/-23,9	-47,40+/-0,17	-42,69+/-0,91	-18+/-47
367= 9L +dL	1140,9+/-10,6	-	-	-41,52+/-0,95	-32+/-55
3611= 5R +dL	1141,4+/-10,6	-868,0+/-23,9	-47,24+/-0,42	-42,75+/-0,29	-12+/-23
3631= 5L +dL	1139,6+/-11,3	-	-	-41,64+/-0,86	-33+/-19
3651= 9R +dL	1145,7+/-10,7	-868,0+/-23,9	-47,45+/-0,13	-42,86+/-0,87	-17+/-47
3671= 9L +dL	1141,6+/-9,2	-	-	-41,57+/-0,82	-37+/-56
386= 3R +dL	1127,7+/-37,0	-868,0+/-23,9	46,71+/-1,24	-42,54+/-1,25	-35+/-30
387= 3L +dL	1121,1+/-33,6	-	-	-40,42+/-1,76	-37+/-36

* значения получены по данным древних астрономов (при работе с их таблицами)

 

А вот с количеством опытов на которые надо разбить всю выборку наблюдений однозначного ответа нет, т.к. по одним параметрам меньше предельные отклонения при 5-и опытах, а по другим при 9-и опытах. Единственное, что можно сказать определенно, так это то, что при 3-х опытах (планы 386 и 387) по всем параметрам, кроме угловой скорости, предельные отклонения получаются больше, чем при 5-и и 9-и опытах. Чтобы понять почему это происходит давайте сравним как изменяются отклонения по dR при обработке примерно одинаковых наблюдательных данных. Возьмем из планов 365, 361 и 386 опыты №1, где  будут обрабатываться данные наблюдений соответственно с 1837 по 1852, с 1837 по 1868 и с 1837 по 1884 годы, т.е. за 16, 32 и 48 лет. Как видно на рис. 16 в первом случае, т.е. на интервале 16 лет отклонения остаются неизменными на всем интервале, а во втором и третьем случае отклонения остаются неизменными только в середине интервале примерно в 20 лет.

 

Рис. 17. Влияние продолжительности опыта на отклонения наблюдательных данных за Солнцем по расстоянию от расчетных при оптимальных параметрах орбиты для каждого опыта.  Скриншот программы Solsys7.

 

Таким образом, можно сделать вывод, что максимальная точность оптимизации параметров орбит будет достигнута, если разбить всю выборку наблюдений на интервалы примерно по 20 лет. Но данное утверждение будет верно только в том случае, если у нас на этом интервале имеется хотя бы 1000 наблюдений. Хотя, если наблюдения выполнены точно то достаточно и 100 наблюдений, но у нас такой уверенности нет и по этому я все же рекомендую разбивать выборку на опыты хотя бы по 1000 наблюдений. А оптимальным я считаю 15...20 опытов по 20 лет, по тому, что при такой выборке можно уже 1 или 2 опыта, которые выпадают из общей зависимости, забраковать и обработав оставшиеся опыты значительно снизить доверительный интервал полученных значений. Например, у меня в данных опытов по Меркурию и Венере получились несколько опытов выпадающих из общей зависимости. У Меркурия это 7-ой опыт, а у Венеры 1-ый, но браковать их я не стал, т.к. у меня маленькие выборки, соответственно, 7 и 8 опытов. К тому же вес этих точек маленький и по этому они не оказывают сильного влияния на вид зависимости.

 

А, если у Вас имеется больше 1000 наблюдений на интервале в 20 лет, то я не рекомендую разбивать их на опыты по 5...10 лет, т.к. высока вероятность, что в такие опыты могут попасть наблюдения только из какой то одной группы и они будут выделяться среди других наблюдений, что приведет к тому, что и полученные оптимальные параметры орбиты в этом опыте будут выделяться из общей зависимости. Я даже ввел корректировку весов отдельных опытов в зависимости от числа наблюдений и продолжительности опытов и чем больше эти величины тем больше увеличивается вес этого опыта. А начальный вес каждого опыта определяется у меня как величина обратная среднему отклонению (по выбранному критерию) всех наблюдений от расчетных значений. И на форме 6, где мы производим статистическую обработку оптимальных параметров во всех опытах, Вы после того, как нажмете на кнопку //Аппроксимировать данные выборки// увидите, что все точки, которые соответствуют отдельным опытам, будут обведены кружками разного диаметра. И чем больше диаметр кружка тем с большим весом эта точка учитывалась при статистической обработке (см. рис. 3, где обрабатывались данные по AlfaP в плане 367 и рис.18, где представлены результаты обработки данных по Eks и Wsr и где, к тому же, в отличие от AlfaP, Betta и AlfaL0, видны получающиеся при этом доверительные интервалы для этих параметров).

 

 

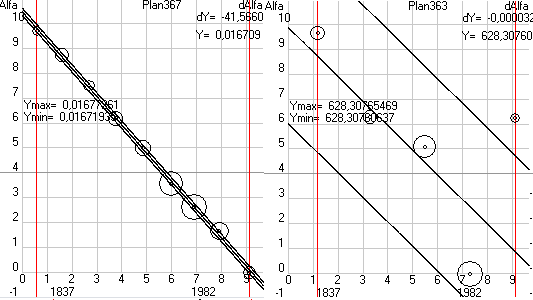
Рис.18. Аппроксимация данных опытов по параметру параметру Eks (план 367) и по Wsr (план 363). Скриншот программы Solsys7.

 

 

Теперь по полученным нами в планах 3611...3671 оптимальным параметрам орбиты Земли находим изменения этих параметров от стандартной эпохи J2000 и получаем кинематическую теорию Земли, которую я буду обозначать как Ser0 (в отличие от моей предварительной теории Ser00). При этом изменение таких параметров, как Betta и AlfaU берем по плану 3651, т.к. оптимизировать эти параметры можно только по критерию dR, а такие параметры как AlfaP, Eks, AlfaL0 и Wsr желательно взять по плану 3671, где оптимизация велась по критерию Abs(dL) с неизменными параметрами Betta и AlfaU, которые мы нашли по плану 3651. Связано это с тем, что наблюдений только по долготе всегда больше, чем и по долготе и по широте, а чем больше мы обрабатываем наблюдений тем точнее должен быть результат. К тому же при этом на результате не будут сказываться ошибки в наблюдениях по широте. А вот при определение зависимости изменения Wsr нам все же придется использовать данные не плана 3671, т.е. с 9-ю опытами, а плана 3631, т.е. с 5-ю опытами, т.к. здесь предельные отклонения получились заметно меньше, чем в плане 3671. На вопросах определения зависимостей для Wsr  и AlfaU (см. рис.19) я еще остановлюсь позже , а сейчас давайте просто запишем получившуюся у нас теорию Земли, т.к. дальнейшее улучшение теории не приводит к изменению параметров (сравните опыты 361...367 и 3611... 3671).

 

AlfaP3 = 102,932543 + 0,317106 * dT (градусы)

AlfaU3 = 354,881105 – 0,241542 * dT (градусы)

Betta3 = -0,000142718 – 0,01318 * dT (градусы)

Eks3 = 0,0167091 – 0,000041566 * dT

AlfaL3 = 100,464217 + 35999,371246 * dT -0,0010632 * dT^2 (градусы)

Wsr3 = 628,307602 – 0,0000328691 * dT (радианы за век)

R3 = 149618,177 + 0,00523493 * dT (тысячи километров)

где dT – время прошедшее от эпохи  J2000 до расчетной даты в юлианских столетиях по солнечному времени, т.е. по UT, а не по эфемеридному времени ET.

 

Эту кинематическую теорию, которая хорошо аппроксимирует изменение параметров орбит в стандартной эпохе J2000 на интервале от 1800 до 2000 годов я назвал Ser0. Если же мы будем при этом учитывать часть самых значимых периодических возмущений от других планет, то это будет уже теория Ser1. Создавать теорию Ser2, где будут учтены десятки или сотни периодических возмущений я не буду, т.к. для основной задачи моего исследования, а именно для поиска скорости гравитации этого не требуется. А вот теорию  Ser0+, которая будет аппроксимировать изменения параметров орбит на интервале в 2000 лет я создам, чтобы после нахождения скорости гравитации проверить показания математической модели созданной с учетом скорости гравитации с данными, которые будет давать кинематическая теория  Ser0+, а также чтобы использовать ее для нахождения по таблицам параметров орбит планет. Кстати выражение для AlfaU3, приведенное выше, взято мною из теории Ser0+, т.е. получено по данным древних астрономов (хотя больше расчетным путем). Связано это с тем, что по наблюдательным данным последних 200 лет определить точно зависимость для  AlfaU ввиду очень маленького угла наклона орбиты Земли к плоскости эклиптики J2000 не возможно. Кстати, и сотрудники JPL не смогли этого сделать даже по данным, полученным на их математической модели и на их сайте, где приведена теория  JPL0 на 200 лет [2], данные по AlfaU вообще отсутствуют, хотя есть в теории на 3000 лет [3] (AlfaU = -5,11260389 – 0,24123856 * dT).

 

А сейчас я дам пояснения откуда у меня в теории появилась зависимость для R, ведь я писал, что найти размер большой полуоси орбит Земли и Луны по наблюдательным данным за Солнцем и Луной не возможно, и затем мы перейдем к созданию теории Ser0+ и нахождению зависимости для AlfaU3. В вопросе нахождения зависимости для R существует сегодня полная неопределенность. Например, Ньюком даже не стал связываться с изменением R и привел их для своей теории неизменными величинами, хотя находил он их по законам Кеплера из Wsr, а для этой величины он приводит зависимости по которым она изменяется. Но изменения Wsr у него получились такие маленькие, например, для Земли -1,953 * 10^-7 рад/век/век (сравните с получившемся у нас -3,287*10^-5 рад/век/век), что он принял R неизменными. А вот авторы современных теорий приводят зависимости с огромными изменениями R, но откуда они берут эти зависимости для меня большой секрет. Например, авторы теории JPL0 приводят следующие зависимости (в астрономических единицах) для 4-х планет Земной группы

R1 = 0,38709927 + 0,00000037 * dT

R2 = 0,72333566 + 0,00000390 * dT

R3 = 1,00000261 + 0,00000562 * dT

R4 = 1,52371034 + 0,00001847 * dT

 

А авторы теории APC2 изложенной в [15] приводят следующие зависимости

R1 = 0,3952829 + 0,0000016 * dT

R2 = 0,7233482 – 0,0000002 * dT

R3 = 1,0001398 – 0,0000007 * dT

R4 = 1,5303352 + 0,0000131 * dT

 

И меня здесь удивляет не только то откуда у них такие гигантские значения вековых изменений большой полуоси, но почему они имеют даже разные знаки в разных теориях. Более, того в своей теории JPL0 для интервала времени в 3000 лет, например, для Земли авторы тоже дают отрицательное значение, хотя на интервале в 200 лет оно было положительное. Конкретно они дают

 

R3 = 1,00000018 – 0,00000003 * dT

 

Я понимаю, что для людей плохо представляющих величину астрономической единицы все эти значения со многими нулями кажутся просто ничтожными, по этому, для наглядности давайте посчитаем какова была бы орбита Земли по этим двум формулам 10 млн. лет тому назад для теории JPL0 на 200 лет и 2 млрд. лет тому назад для теории JPL0 на 3000 лет. Да, экстраполировать на такие интервалы по этим теориям нельзя, но для здравого смысла полезно посмотреть, что получиться. Для 10 млн. лет получается 65,5 млн. км., т.е. примерно орбита Меркурия (57,9 млн.км.), а для 2 млрд. лет получается 239,4 млн.км., т.е. примерно орбита Марса (227,9 млн.км.). Причем, обе эти зависимости были получены ими при обработке расчетных данных, которые были получены на одной и той же математической модели Солнечной системы. Вот только я ума не приложу, как они могли получить такие зависимости, т.к. я обработав их данные полученные по теории JPL2, т.е. эфемериды DE405 не обнаружил никакого изменения ни Wsr ни R. В общем оставим на совести авторов манипуляции позволившие получить им вышеприведенные зависимости и обратимся к данным, которые получились у нас.

 

Посчитаем по полученной нами зависимости для  Wsr угловую скорость в рад/сек для эпохи J2000 и для времени 10 млн. лет тому назад. При этом в расчете я возьму не приведенное выше значение 3,287*10^-5 рад/век/век, а 3,31216 * 10^-5, которое у меня получилось в одном из вариантов расчета, т.к. там получилась дисперсия (предельные отклонения) меньше чем по плану 3651 приведенному в таблице 4 (в этой статье я привожу только часть различных вариаций выполненных мною планов). У нас получится

Wsr(J2000) = 628,307601 / 36525 / 24 / 3600 = 1,9909866 * 10^-7 (рад/с)

Wsr(-10) = 628,307601 + 3,31216 * 10^-5 * 10^5 = 631,61976 / 36525 / 24 /3600 = 2,0014822 * 10^-7

 

Теперь предположим, что Земля движется по круговой орбите (при малом эксцентриситете орбиты Земли это вполне допустимо). Тогда, исходя из того, что центробежная сила должна быть равна силе притяжения Солнца можем записать

gamma * m0 * m3 / R^2 = m3 * Wsr^2 * R

где: gamma = 6,67259 (н * м^2 / кг^2), m0 = 1,98976 * 10^30 (кг)

отсюда

R = (gamma * m0 / Wsr^2)^0,33     (6)

 

Подставляем в эту формулу значения Wsr(J2000) и Wsr(-10) и находим R(J2000) = 1,49618177 * 10^11 (м) и R(-10) = 1,4909468 * 10^11 (м). Таким образом за 10 млн. лет радиус орбиты Земли увеличился на 523,493 тыс.км. и следовательно вековое изменение радиуса орбиты будет +0,00523493 тыс.км/век. Да, это у нас получилось не изменение большой полуоси R, а изменение среднего радиуса круговой орбиты и изменение угловой скорости в нашей теории получилось со значительным предельным отклонением и по этому данная зависимость изменения большой полуоси орбиты Земли не совсем точная, но это гораздо лучше того, что предлагают современные теории планет. А знать зависимость по которой будет изменяться R Земли нам обязательно надо, т.к. от этого зависит какие получатся параметры орбит у других планет, которые наблюдали из определенной точки в пространстве, где находилась в этот момент Земля.

 

И маленькое пояснение по поводу периодических возмущений, учитываемых мною при обработке данных. На рис. 14 Вы видите полученные мною значения возмущений по данным файла SUMM0_G_200L, для теории JPL0, а сейчас, после получения теории Ser0, в программе уже немного другие значения, которые получены по данным файла SUMM0_G_201L, для теории Ser0. Аналогично я поступал и с периодическими возмущениями для планет. По мере уточнения их теорий я уточнял и значения периодических возмущений для этих теорий. Сейчас у меня используются значения приведенные в табл. 6.

 

Таблица 6. Периодические возмущения планет от 2-х других планет (номера 1-ой и 2-ой планеты даны после названия планет)

	Меркурий 2,5	Венера 3,5	Земля 2,5	Марс 3,5
dL3(1)	-0,00102	+0,00032	-0,00005	-0,00041
dL4(1)	+0,00012	-0,00426	+0,00155	-0,00195
dL7(1)	-0,00030	+0,00075	-0,00136	+0,00335
dL5(1)	+0,00015	+0,00051	+0,00001	+0,00365
dL8(1)	+0,00000	-0,00003	-0,00000	-0,00056
dL9(1)	-0,00007	+0,00003	+0,00000	-0,00107
dL10(1)	-0,00012	-0,00017	-0,00072	-0,00410
dL21(1)	-0,00013	+0,00144	-0,00000	-0,00004
dL3(2)	-0,00114	-0,00004	-0,00042	-0,00574
dL4(2)	+0,00073	+0,00022	+0,00076	+0,00408
dL7(2)	+0,00046	-0,00040	-0,00200	-0,00731
dL5(2)	-0,00011	-0,00044	-0,00066	-0,00007
dL8(2)	+0,00017	+0,00000	+0,00000	+0,00072
dL9(2)	+0,00021	+0,00083	+0,00007	+0,00004
dL10(2)	+0,00029	+0,00018	+0,00001	+0,00051
dL21(2)	-0,00009	-0,00019	-0,00016	+0,00066

 

А теперь переходим к созданию теории Ser0+, где мы будем использовать не только параметры орбит, полученные нами по данным оптических наблюдений за последние 200 лет, но и параметры орбит, которые были получены древними астрономами по оптическим наблюдениям тех лет. Для некоторых теорий древних астрономов можно и не определять значения параметров использованных в них, а взять напрямую из описания теорий, например, для теории Стрита. Но, во-первых, не все теории так хорошо описаны как его, а, во-вторых, в тех случаях, когда в теориях планеты движутся не по эллипсам вокруг Солнца, а по сложному нагромождению эксцентров вокруг Земли, сделать это напрямую не возможно. По этому, для всех теорий древних астрономов, которые оформлены ими в виде таблиц для расчета геоцентрических эклиптических координат светил, мы для нахождения параметров орбит, заложенных в их расчеты, применим методику по которой мы обрабатывали данные современных наблюдений. При этом отдельными наблюдениями будем считать координаты рассчитанные по таблицам на интервале в 30 лет через 1,28 дня. Интервал я взял не 20, а 30 лет по тому, что данные, рассчитанные по таблицам созданным до Кеплера, отличаются из-за неэллиптичности орбит от наших расчетных данных с периодом равным периоду обращения планет и, чтобы уменьшить влияние этой цикличности на критерий оптимизации надо, чтобы число этих периодов в интервале было как можно больше. Итого за 30 лет будет 8572 наблюдения, т.е. вполне представительная выборка, но здесь у нас возникает масса других проблем.

 

Я уже писал о том, что даты создания тех или иных таблиц мне известны приблизительно, а следовательно и полученные по этим таблицам оптимальные параметры будут найдены с погрешностью по времени наблюдения. Часть теорий древних астрономов построена на том, что это Солнце движется вокруг Земли, а не барицентр Земля-Луна вокруг Солнца и при этом у них, естественно, не происходит никаких колебаний Земли относительно барицентра, а в программе у меня заложена такая методика определения расчетных координат Земли, когда учитываются эти колебания. Таким образом, я буду вносить периодические погрешности в расчетные координаты Земли, что несколько снизит точность нахождения параметров орбит заложенных в теории древних астрономов. А вот нутацию вводить в расчетные координаты, чтобы их сделать видимыми, я  точно  не буду, т.к. в теориях древних астрономов она точно не отражена и добавление погрешности наблюдений от нутации тоже, как и от барицентра, только снизит точность нахождения параметров орбит. И поправку на параллакс я учитывать не буду т.к., пусть и с ошибками, но во всех этих теориях она уже учтена и мы имеем в таблицах геоцентрические эклиптические координаты, а вот с учетом рефракции очень много вопросов.

 

Во-первых, нет уверенности, что древние астрономы до появления таблиц Кеплера совсем не учитывали рефракции, а если не учитывали, то как ее учесть в их расчетных координатах, которые мы используем как видимые, т.е. наблюдаемые. Если бы мы имели отдельные реальные наблюдения древних астрономов, то нет проблем, но мы имеем сглаженные единой теорией отдельные наблюдения, где были разные значения рефракции. По этому я не вижу как можно учесть рефракцию в расчетных координатах древних астрономов, хотя и предусмотрел в программе функцию //+Видимость//, чтобы обрабатывать только те расчетные положения планет, когда планеты реально видны в это время. Для наблюдений за Солнцем и Луной погрешность от рефракции будет незначительной, а вот для Меркурия и Венеры это будет уже заметная погрешность и это тоже снизит точность найденных параметров орбит по таблицам древних астрономов до Кеплера. Здесь надо заметить, что и сама точность определения координат при наблюдениях у астрономов до Тихо Браге была примерно четверть градуса и по этому отличаться особой точностью параметры, полученные нами по таблицам древних астрономов, конечно же не будут, но для нас очень важно использовать их хотя бы как ориентиры на интервале в 2000 лет. Хотя, данные по AlfaL0 могут оказаться для нас очень ценными, т.к. никаким математическим моделированием в эфемеридном времени эти данные в солнечном времени не получить.

 

Таким образом, мы будем по таблицам древних астрономов получать как бы наблюдаемые данные и затем сравнивать их с координатами рассчитанными по оптимизируемым нами параметрам эллиптических орбит и при этом в наши расчетные координаты, чтобы их сделать видимыми, т.е. наблюдаемыми, вносить только поправки вызванные планетной и звездной аберрациями, которые естественным образом отражены в таблицах. А, т.к. в этом случае у нас в наблюдаемых данных всегда будут и долгота и широта, то дополнительную оптимизацию параметров орбит Земли и Луны по критерию Abs(dL) мы делать не будем. При этом, значение параметра R для наблюдаемых данных мы, как и при обработке данных оптических наблюдений, всегда будем брать равным расчетному значению. Сначала мы выполним оптимизацию по плану 32 и получим параметры орбит с той прецессией, которая заложена в таблицах, а потом для тех таблиц, где прецессию можно исправить на современное значение, выполним план 33, чтобы уточнить параметры. При этом данные по таблицам, где прецессию нельзя исправить (она там входит в скорость перемещения Солнца вокруг Земли) мы перенесем в план 33, но возьмем вес этих опытов в 10 раз меньше, чем у опытов с исправленной прецессией. Затем мы данные плана 33 объединим с данными оптических наблюдений плана 3671 (см. табл. 5) и у нас получится план  368 и с данными плана 3651 (получится план 366). При этом, данные, полученные по каждой таблице, будут соответствовать одному опыты при обработке файла оптических наблюдений.

 

Таблица 7. Параметры орбиты Земли полученные мною при обработке данных из таблиц древних астрономов и данных наблюдений за последние 200 лет (план 366, критерий dR в тыс.км.).

 

данные наблюдений	dR	вес	AlfaP	AlfaU	Betta	Eks	Wsr
Almagest -141...-112	41,7	0,01	95,095	360,011	0,2817	0,020767	628,30707
AlKhwarizmi 800...829	46,2	0,01	98,297	357,742	0,1560	0,019438	628,30415
AlBattani 900...929	20,8	0,001	97,890	357,502	0,1427	0,017323	628,31048
Alfonso 1252...1281	30,3	0,01	98,518	356,659	0,0962	0,018898	628,31233
Ticho 1580...1609	34,3	0,001	101,238	355,868	0,0529	0,017970	628,30757
Rudolphine 1620...1649	4,03	0,01	101,357	355,812	0,0504	0,018000	628,30701
Streete 1620...1649	3,81	0,01	101,494	355,765	0,0478	0,017320	628,30839
Wing 1640...1669	24,9	0,001	101,468	355,720	0,0450	0,017878	628,30719
1       1837...1852	3,52	1,14	102,448	354,653	0,0202	0,016774	628,30769
2       1853...1868	2,55	1,63	102,487	354,488	0,0182	0,016769	628,30771
3       1869...1884	2,44	1,50	102,540	354,224	0,0161	0,016762	628,30768
4       1885...1900	2,31	1,91	102,597	353,746	0,0140	0,016754	628,30768
5       1901...1916	2,33	2,27	102,644	354,351	0,0117	0,016748	628,30771
6       1917...1932	2,06	3,50	102,702	354,173	0,0095	0,016739	628,30765
7       1933...1948	2,29	3,66	102,745	354,519	0,0077	0,016734	628,30767
8       1949...1964	2,21	2,49	102,791	354,308	0,0057	0,016728	628,30774
9       1965...1980	2,14	1,57	102,849	356,860	0,0034	0,016720	628,30764

 

В этой таблице Вы видите не только сами параметры орбит, но и веса каждого опыта, которые учитывались при статистической обработке этих данных. Как я уже писал, в общем случае вес каждого опыта (точки на графике формы 6) равен единице деленной на значение критерия в данном опыте, но Вы видите, что у опытов 1...9 это не так и их вес явно больше 0,5 (1/2). Это следствие того, что в дальнейшем я корректировал эти веса в зависимости от числа наблюдений в данном опыте и интервала за который обрабатываются данные. А, т.к. в опытах 1...9 у нас кругом интервал был 16 лет, то, следовательно, отличие в весах связано только с количеством наблюдений в опыте. Например, в опытах 7, 8, 9 было примерно одинаковое значение критерия оптимизации dR (среднего отклонения по расстоянию наблюдаемых и расчетных данных) но было разное количество наблюдений 6286, 3790 и 1916, а отсюда и такое различие в весах этих опытов. При этом, приведенные значения dR, являются минимально возможными значениями средних отклонений, т.е. полученными при оптимальных значениях параметров эллиптической орбиты Земли, если сравнивать рассчитанные по этим параметрам координаты Земли и данные оптических наблюдений или данные полученные по таблицам древних астрономов.

 

А вот вес данных, полученных по таблицам я задавал произвольно, т.к., если применить к ним методику для уточнения веса оптических наблюдений, то задав очень маленький шаг (в днях), через который по таблицам будут рассчитываться координаты планет, мы можем получить очень большую выборку и искусственно повысить их вес. А первоначальные веса этих опытов, как Вы можете посчитать сами, будут от 0,0216 у АльХорезми до 0,262 у Стрита. Но, как я писал выше, при работе с таблицами древних астрономов существует много вопросов по тому, какие поправки они учитывали обрабатывая данные реальных оптических наблюдений, положенных в создаваемые ими теории, по этому, я и задал их данным максимальный вес 0,01. Хотя, например, для таблиц Кеплера, Стрита и Винга вес можно было бы взять и побольше, т.к. у них созданы гелиоцентрические теории планет и движутся у них планеты уже по эллипсам, а в наблюдениях учтена рефракция. Правда, здесь возникает вопрос с теорией Винга, которая дает отклонения от эллиптических орбит (dR) примерно такое же как и геоцентрические теории с эксцентрами и эпициклами. Но при создание этих теорий их авторы использовали не только наблюдения выполненные Тихо Браге, но и данные наблюдений, выполненных еще Гиппархом. К тому же они тоже использовали не правильное значение параллакса Солнца. По этому, я и принял для них тоже такие маленькие веса.

 

А то, что в теориях Кеплера и Стрита получились малые отклонения эллиптических орбит от эллиптических орбит (критерий dR), то так оно и должно было быть и точность определения параметров орбит заложенных в этих теориях тоже получилась высокой. Например, Стрит заложил в таблицы Eks=0,01732 и у меня получилось Eks=0,01732. А Птолемей заложил в свои геоцентрические таблицы Eks=0,0207 (если взять как половину эксцентриситета эксцентра), а у меня получилось Eks=0,02077. Таким образом моя методика применима не только для таблиц с эллиптическими орбитами, а с любыми примененными орбитами планет.

 

При создание теории Ser0+ я буду использовать данные нескольких планов, но приводить параметры орбит, полученные мною во всех планах, я не буду т.к. это слишком много информации и кто заинтересуется какими то конкретными данными сможет их посмотреть скачав программу Solsys7, т.к. вместе с самой программой я выложу и все файлы наблюдательных данных и таблицы древних астрономов, которые я использовал, а также данные всех планов с полученными параметрами орбит. При этом, если Вы будете повторять на программе Solsys7 эксперименты, аналогичные проведенным мною, то Вы можете получить данные, которые будут немного отличаться от приведенных мною как в этой таблице так и в других. Это связано во-первых с тем, что я постоянно вношу какие то изменения или уточнения в свою программу Solsys7 и сейчас, когда пишу этот абзац статьи, я работаю уже с 14-м вариантом этой программы. При этом я, например, в 13-м варианте увеличил точность записи параметров в файлы опытов с 6-и до 9-и знаков после запятой и стал определять дату середины интервала обрабатываемых данных, не строго посередине календарного интервала, а как среднюю дату из дат всех наблюдений, но все эти уточнения никак не должны повлиять принципиально на полученные мною ранее результаты.

 

А во-вторых, расхождения возможны из-за того, что мы просто будем не в той последовательности выполнять два подплана 6-и или 8-и факторного эксперимента. Например, я сначала оптимизирую первые 4-е параметра из 6-и, а потом 2-а вторые, а Вы наоборот сначала оптимизируете первые 2-а параметра из 6-и, а потом 4-е вторые.  Но все это не принципиально и обрабатывая как полученные мною данные, так и те, что Вы получите самостоятельно работая с программой  Solsys7, мы будем иметь аналогичные зависимости для изменения параметров орбиты Земли. Хотя, даже, у меня в совершенно идентичных опытах получаются немного разные данные. Например, получилось так, что последние опыты в планах 361 и 365 обрабатывались по одному и тому же критерию dR а в планах 363 и 367 по критерию Abs(dL) и интервал наблюдательных данных в этих опытах был кругом с 1965 по 1980 годы (в 361 и 363 планах хватило наблюдений только на половину 32-х летнего интервала). В таком случае можно было бы в идентичных опытах не производить оптимизацию в каждом из них, а скопировать во второй план полученные в первом плане оптимальные параметры, но я автоматически провел независимую оптимизацию во всех 4-х случаях и получил следующие данные по перигелию Земли.

AlfaP361(5R)=102,849443                         AlfaP363(5L)=102,849274

AlfaP365(9R)=102,849232                         AlfaP367(9L)=102,848951

Как видим, по критерию dR расхождение получилось 0,000211, а по критерию Abs(dL) получилось 0,000323 (градуса). Интервал варьирования параметра AlfaP в планах был 0,02 градуса, а точности я добивался +/-0,01 интервала, т.е. получится +/-0,0002 градуса. Таким образом и в первом и во втором случаях я добился требуемой точности и полученные значения параметра AlfaP не выходят за доверительный интервал.

 

Для нахождения зависимостей изменения параметров орбиты Земли AlfaP, Eks и AlfaL0 мы будем использовать план 368, а для нахождения Wsr план 364 и для AlfaU и Betta план 366. Хотя и для AlfaU и Betta можно было бы использовать план 368, т.к. эти параметры в этом плане не уточнялись по критерию Abs(dL), а остались такими как они были в плане 366, но я принципиально разделил эти планы, т.к. оптимизация в них шла по разным критериям, где учитывалось разное количество наблюдений, и по этому получились немного разные даты для середины интервала обрабатываемых данных, т.е. для дат, для которых эти параметры оптимальны. Можно бы было и зависимость для Wsr тоже сделать по плану 368, но доверительный интервал в плане 364 поWsr получился гораздо меньше и по этому я буду использовать данные именно этого плана. В результате у меня получились вот такие зависимости для теории Ser0+ .

 

AlfaP3 = 102,930604 + 0,31131 * dT – 0,00349204 * dT^2

AlfaU3 = 354,88747 – 0,24111 * dT

Betta3 = - 0,000143778 – 0,0131812 * dT

Eks3 = 0,0167144 – 0,0000265732 * dT - 0,00000868624 * dT^2

AlfaL3 = 100,46501957 + 35999,37325813 * dT

Wsr3 = 628,307603 – 0,0000312939 * dT

R3 = 149618,177 + 0,00523493 * dT

 

А теперь давайте более подробно рассмотрим определение AlfaU для наших теорий. На рис. 19 приведены данные плана 366 (синие точки), где мы видим, что данные таблиц хорошо ложатся на прямую, а данные оптических наблюдений за последние 200 лет (план 365) получились с очень большим разбросом и немного все (кроме последнего опыта) смещенными вниз. Большой разброс объясняется очень маленьким наклоном орбиты к плоскости фиксированной эклиптики эпохи J2000, т.к. при таком наклоне влияние этого параметра на критерий оптимизации будет очень маленьким. А т.к. я оптимизировал параметры так, чтобы влияние их на критерий оптимизации было примерно одинаковым, то мне пришлось задавать очень большой интервал варьирования этого параметра (от 3 до 8 градусов). Учитывая, что я добивался точности до 0,01 интервала, получится, что оптимизировал я этот параметр с точностью до 0,03...0,08 градуса, а это очень много. К тому же периодические возмущения сильно влияют на значение AlfaU. А вот смещение всех этих данных ниже зависимости полученной по данным таблиц объясняется не точностью центровки данных наблюдений, которую мы проводили выше по теории JPL2. И если теперь данные в файле SUMM0_G_200 увеличить по долготе на 1 угл.сек, то оптимальные значения параметра AlfaU в плане 376 по новому файлу SUMM0_G_220LB (красные точки) поднимутся и будут лежать с обоих сторон от прямой аппроксимирующей данные таблиц (красная линия на рис.19).

 

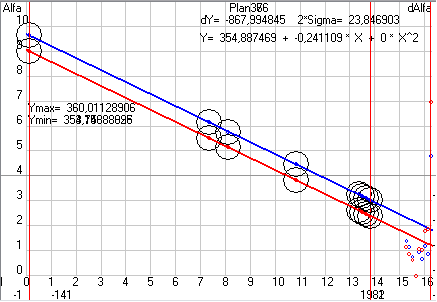
Рис.19. Аппроксимация данных опытов по планам 366 (синие точки) и 376 (красные точки) по параметру AlfaU. Скриншот программы Solsys7.

 

Для получения зависимости AlfaU я использовал только данные таблиц по тому что учет еще и данных оптических наблюдений только ухудшит результат. Для этого перед тем как нажать кнопку //Аппроксимировать данные выборки// надо изменить номер последней точки в выборке (щелкнуть правой кнопкой мыши по нужной последней точке). При этом, ввиду того, что оптимальные значения AlfaU по таблицам получились все таки расчетными, т.к. таблицы составлены для эпохи даты и там просто не может быть для Земли Betta и AlfaU, я принял веса всех опытов по таблицам равными единице (отметил чекбокс //+Ves=1//). Как Вы видите, у нас не получилось при наложение данных плана 376 на данные плана 366 равномерного смещения красных точек относительно синих и к тому же сместились не точки оптических наблюдений, но и точки из таблиц древних астрономов. Это объясняется тем, что при наложение одних данных на другие у меня в программе отсчет ординат точек идет от минимальной ординаты в первом плане, на который накладываются данные второго плана. По этому не красные точки оптических наблюдений приблизились к красной линии данных таблиц, а наоборот. Как видим красные точки при этом (кроме самой нижней) не накрыли точно синие точки. Это объясняется тем, что файл 220LB делался мною давно, а отбраковку я тогда вел по теории JPL0 и dRmax брал не 5 тыс.км., как сейчас для файла 201LB (план 366), а 6 тыс.км. Но все это не столь важно, т.к. главным здесь является то, что расхождение в AlfaU полученном по таблицам и по данным оптических наблюдений объясняется просто не точной центровкой данных оптических наблюдений, которая искажает только определение параметров AlfaU и AlfaL0.

 

Что касается аппроксимации данных по другим параметрам орбиты Земли, то здесь никаких неожиданностей и все они, хотя и гораздо хуже чем в теории Ser0, но все же более менее укладываются в какую то зависимость. И ниже я привожу скриншоты программы Solsys7 с аппроксимацией параметров орбиты Земли для теории Ser0+. Что касается скриншота аппроксимации параметра AlfaL0, то я его не привожу по той простой причине, что там угол изменяется от -770285 градусов у Птолемея до -12498 градусов в опыте №9, что при любом масштабе на рисунке даст идеальную прямую. На всякий случай на скриншотах я вывел на рисунок и зависимости аппроксимирующие данные этих опытов.

 

 

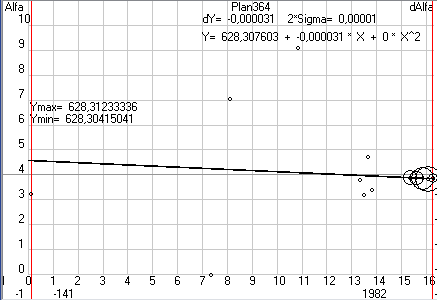
Рис.20. Аппроксимация данных опытов по плану 364 по параметру Wsr. Скриншот программы Solsys7.

 

 

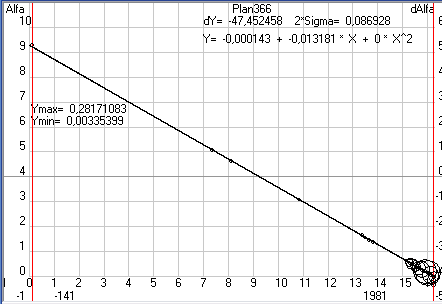
Рис.21. Аппроксимация данных опытов по плану 366 по параметру Betta. Скриншот программы Solsys7.

 

 

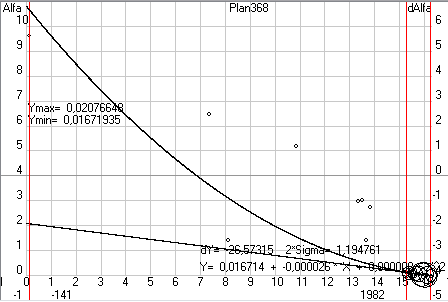
Рис.22. Аппроксимация данных опытов по плану 368 по параметру Eks. Скриншот программы Solsys7.

 

 

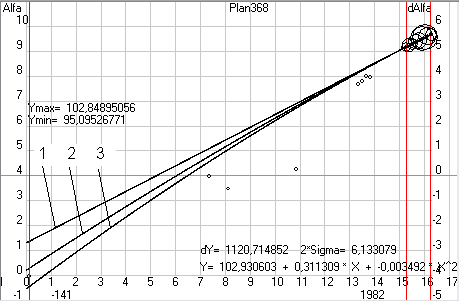
Рис.23. Аппроксимация данных опытов по плану 368 по параметру AlfaP. Скриншот программы Solsys7.

 

Как видим, параметр Betta и здесь отлично аппроксимируется прямой, а по параметру Wsr хотя и имеется большой разброс данных в таблицах древних астрономов, но малый вес этих точек не сильно изменяет зависимость полученную нами для теории Ser0. У тех, кто не знаком с первой частью этого цикла статей [16], может возникнуть много вопросов по параметрам Eks и AlfaP, но пересказывать еще раз то, что написано в первой части я не буду, а просто отправлю их к этой статье, хотя сейчас у меня уже появились и некоторые другие мысли. Что касается параметра AlfaP, то быстрее всего он так и изменяется по квадратичной зависимости (3) потому что даже, если мы аппроксимируем только данные оптических наблюдений, то мы тоже получим квадратичную аппроксимацию (2), которая будет значительно отличаться от линейной (1). А чтобы аппроксимировать данные только оптических наблюдений, надо щелкнуть левой кнопкой мыши по точке 1-го опыта. Как подтверждение правильного выбора начала выборки для статистической обработки Вы увидите вертикальную красную линию, которая будет проходить через эту точку, а в окошке //начальная точка №// Вы увидите номер этой точки и дату начала интервала этого опыта (точки) начиная с которой будут обрабатываться данные при статистической обработке данных.

 

Что касается аппроксимации опытов по параметру Eks, то я сейчас считаю, что зависимость так и должна остаться квадратичной, но кривизна этой зависимости должна быть гораздо меньше, чем у нас получилось, но не быть прямолинейной, как это получается по данным только оптических наблюдений за последние 200 лет. Но до тех пор пока я не найду скорость гравитации я буду считать, что параметр Eks изменяется именно по той зависимости, что у нас получилась. И напоследок несколько замечаний по поводу того, что на рисунках Вы в правом нижнем углу видите не 1980 год, т.е. последний год последнего интервала (опыта) за который мы аппроксимировали данные наблюдений, а 1981 или 1982 год. Это связано с тем, что на форме 6 последний год интервала рассчитывается как год начала интервала плюс две продолжительности до средней величины середины интервала, которая не всегда совпадает с календарной серединой интервала. И в том случае, если наблюдений будет больше в конце интервала, то и значение средины интервала будет больше значения календарной середины интервала. При этом 1981 или 1982 год появляется по тому, что количество наблюдений по dR и dL, а также их распределение по интервалу будут разными. А год начала первого опыта -141 (142 год до нашей эры) это год когда делал свои наблюдения Гиппарх, по данным которого Птолемей в 137 году нашей эры и составил свои таблицы, по этому и полученные по таблицам Almagest параметры орбиты Земли следует считать оптимальными для -141 года.

 

А теперь давайте для теории Луны также обработаем на форме 10 данные таблиц древних астрономов и оптических наблюдений из полученного нами ранее файла SUMM11_G_300, данные в котором еще раз отбракуем с поправками от периодических возмущений, т.е. не по теории JPL0, а по теории JPL1 по расстоянию +/-0,4 тыс.км. и получим файл SUMM11_G_301LB. Правда, теория JPL0 никакого отношения к теории Луны, по которой мы будем отбраковывать данные оптических наблюдений, не имеет, т.к. у JPL нет аналитической теории Луны. И отмечая переключатель JPL0 мы будем выбирать упрощенную теорию Луны, которую я скомпилировал из работ [12, 15 ]. Точно также, как и для Земли, потом полученные данные по параметрам орбиты Луны обрабатываем на форме 6 и получаем кинематическую теорию Луны. Вот только данных оптических наблюдений у меня очень мало и все они за 19-ый век, по этому создавать теорию Ser0 для Луны я не буду, а сразу создам теорию Ser0+. Отличительной особенностью при обработке данных по Луне у нас будет то, что параметры AlfaP и AlfaU изменяются так быстро, что даже для года нельзя задать их неизменными, и по этому будем их задавать также как AlfaL по формуле (4). Только вместо AlfaL0 у нас будут AlfaP0 и AlfaU0, а вместо Wsr будут dP11 и dU11. На форме 13 это 8-ой и 9-ый факторы.

 

Итого нам надо выполнить восьмифакторный план, но программа позволяет сделать только шестифакторный план, по этому я его разбил на два 4-х факторных плана и выполнял их поочередно пока не добился заданной точности. Продолжительности опытов для обработки данных оптических наблюдений в планах 115 и 116 я брал согласно таблице 8, а параметры по таблицам древних астрономов я обрабатывал за тот же интервал, что и данные наблюдений за Солнцем. И также, как и в планах 32 и 33 для Солнца, я для Луны в плане 112 тоже сначала нашел параметры с прецессией заложенной в таблицах, а затем в плане 113 уточнил их с исправленной прецессией (там где можно было). При этом, также как и для наблюдений за Солнцем задал веса параметрам найденным по таблицам гораздо меньше чем они получились в опытах при обработке данных оптических наблюдений (см. таблицу 9). А, т.к. у АльХорезми получились параметры явно выпадающие из общей зависимости я для его параметров задал вес равный нулю, т.е. его данные только выводятся на график, но в статистической обработке данных участия не принимают. А ввиду того, что у меня совершенно нет данных наблюдений за 20-ый век, я решил в выборку добавить и одну расчетную точку из современных теорий, а конкретно параметры на эпоху J2000 и взял для нее вес такой, какой был у оптических наблюдений.

 

Таблица 8. Интервалы опытов для обработки данных наблюдений за Луной.

1	1800-1842 / 2237	1800-1819 / 1207
2	1843-1991 / 4036	1820-1940 / 911
3		1841-1859 / 1563
4		1860-1869 / 1300
5		1870-1891 / 1291

 

При обработке данных оптических наблюдений я использовал для учета периодических возмущений вызванных притяжением Солнца поправки из теории Брауна, которые Вы видели на рис. 13 (только те, что отмечены галочкой). А для таблиц древних астрономов я использовал только те поправки, которые были учтены в их таблицах. АльХорезми вообще не учитывал никаких поправок, а Птолемей, АльБаттани и Альфонсо учитывали только эвекцию, если не считать поправок от 1-го и 2-го главных неравенств, которые нам учитывать не надо, т.к. мы задаем параметры эллиптической орбиты. А вот для таблиц начиная с Тихо Браге я учитывал дополнительно поправки от вариации, годичного неравенства и вариации по широте. При этом для таблиц до Тихо Браге я брал современное значение эвекции -1,2739, а начиная с таблиц Тихо Браге я эвекцию и вариацию подбирал для каждой таблицы индивидуально (Тихо Браге -1,18 и 0,75, Кеплер -1,15 и 0,9, Стрит -1,2 и 0,71, Винг -1,18 и 0,74). При этом, для этих четырех таблиц я брал современные значения годичного неравенства -0,1856 и вариации по широте 0,1732 (градуса).

 

Таблица 9. Параметры орбиты Луны полученные мною при обработке данных из таблиц древних астрономов и данных оптических наблюдений за предпоследние 100 лет (план 115). Здесь dAlfaP и dAlfaU вековые смещения этих параметров, т.к. сами углы изменяются очень быстро и их значения будут сопоставимы со значениями AlfaL0 и их значения в табличном виде нам ни о чем не скажут.

 

данные наблюдений	dR	вес	dAlfaP	dAlfaU	Betta	Eks	Wsr
Almagest -141...-112	2,162	0,2	70,9955	-33,6425	5,0474	0,053911	8399,6821
AlKhwarizmi 800...829	0,975	0,0	70,9913	-33,8740	4,4612	0,042748	8399,6832
AlBattani 900...929	1,756	0,02	70,9962	-33,7519	5,0081	0,053966	8399,6864
Alfonso 1252...1281	1,653	0,2	71,0051	-33,7763	4,9942	0,053224	8399,6888
Ticho 1580...1609	1,129	0,02	71,0000	-33,7990	5,1238	0,054286	8399,6831
Rudolphine 1620...1649	1,029	0,2	70,9967	-33,8025	5,1527	0,054516	8399,6825
Streete 1620...1649	1,017	0,2	70,9967	-33,8012	5,1395	0,054718	8399,6840
Wing 1640...1669	1,027	0,02	70,9976	-33,7969	5,1365	0,053994	8399,6828
1       1800...1819	0,179	25,73	70,9965	-33,7841	5,1501	0,054884	8399,6850
2       1820...1840	0,162	46,04	70,9957	-33,7839	5,1402	0,054881	8399,6850
3       2000...2000	0,000	35,00	70,9937	-33,7814	5,1444	0,054900	8399,6847

 

Как Вы заметили, в таблице 9 я не только привожу не сами параметры AlfaP и AlfaU, а их вековые смещения (рад/век), но и привожу данные по опытам с оптическими наблюдениями когда я всю выборку разбил на два опыта по 43 и 48 лет, хотя, как мы убедились обрабатывая данные наблюдений за Солнцем, что при таких интервалах возникают большие отклонения расчетных данных от наблюдаемых (см. рис. 17). Но давайте посмотрим на рис. 24, где я привожу отклонения по критерию dR во втором опыте 185 плана (с 1843 по 1891 годы) и в пятом опыте 186 плана (с 1870 по 1891 годы). Эффект краев интервала исчез и отклонения на всем интервале 185 плана такие же, как и на маленьком интервале 186 плана. А объяснить это можно только тем, что и на длинном интервале оптимальные параметры орбиты, которые больше всего подходят для середины интервала, оставались тоже почти оптимальными и на краях этого интервала. В самом деле и AlfaP и AlfaU у нас теперь рассчитывались по формуле аналогичной (4) как оптимальные чуть ли не для каждого отдельного наблюдения, а Eks и Betta, как видно на рис. 25, изменяли свои значения очень незначительно. И, если мы все параметры орбиты будем задавать по формуле (4), то мы можем для всех планет задавать интервалы опытов почти в 100 лет. Естественно, мы этого делать не будем, т.к. это усложнит расчеты и к тому же у нас просто нет столько наблюдательных данных, но при длинных интервалах мы можем лучше погасить неучтенные периодические возмущения и по этому я и для Меркурия, Венеры и Марса тоже попробую разбить выборку на длинные интервалы.

 

 

 

 

Рис.24. Влияние продолжительности опыта на отклонения наблюдательных данных за Луной от расчетных по расстоянию при оптимальных параметрах орбиты для каждого опыта. Скриншот программы Solsys7.

 

 

Рис.25. Изменение параметров Betta11 и Eks11 от -141 до 2000 года. Скриншот программы Solsys7.

 

 

 

Рис.26. Изменение Wsr Луны при аппроксимации данных планов 115 и 116. Скриншот программы Solsys7.

 

На рис. 26 приведены данные по Wsr для 115 и 116 планов и здесь мы также, как и при обработке данных наблюдений за Солнцем, видим, что длинные интервалы позволяют более точно найти оптимальные значения Wsr. Быстрее всего это связано с тем, что параметр Wsr изменяется очень медленно и его изменение впору называть не вековым, а тысячелетним смещением этого параметра. По этому, для нахождения достоверного смещения этого параметра нужна выборка данных не за 200 лет, а за 2000 лет. Вообще то у нас такая выборка для теории Ser0+ есть, но точность данных древних астрономов не достаточна, чтобы достоверно выявить изменение этого параметра. То же самое очевидно относится и к размеру большой полуоси орбиты планет, т.к. Wsr и R жестко функционально связаны. Учитывая также то, что сами смещения параметров орбиты Луны меня не очень интересуют, т.к. вызваны они (особенно смещение AlfaP и AlfaU) явно не влиянием других планет, я решил принять для изменения параметра орбиты Луны R зависимости (5-1), т.е. принять его на всем интервале от 0-го до 2000 года неизменным. Итого кинематическая теория Луны Ser0+ будет выглядеть так.

 

AlfaP11 = 83,354172 + 4067,633745 * dT – 0,00896623 * dT^2

AlfaU11 = 125,053825 – 1935,568239 * dT – 0,00342738 * dT^2

Betta11 = 5,147415 + 0,00364811 * dT

Eks11 = 0,0549329 + 0,0000473381 * dT

AlfaL11 = 218,318785 + 481266,497751 * dT + 0,00339164 * dT^2

Wsr11 = 8399,684874 – 0,00000272265 * dT

R11 = 384,402

 

Что касается изменения величины большой полуоси орбиты Луны R11, то можно было бы рассчитать так, как мы это делали для орбиты Земли, и ее изменение, но для моего исследования этого не требуется по этому я ее принимаю неизменной и беру ее современное значение. Для расчета Лунных и Солнечных затмений это конечно же будет вносить погрешность, но мне теория Луны нужна только для того, чтобы из координат барицентра Земля-Луна найти координаты Земли, а здесь эта погрешность будет просто микроскопической. К тому же у меня было очень мало наблюдательных данных по Луне и только за 19-ый век, по этому этот расчет будет очень приблизительным. А точность полученной нами теории Луны мы можем проверить уже сейчас по нескольким солнечным затмениям, т.к. их параметры будут определяться в основном качеством теории Луны, т.к. вклад в это теории Земли будет на порядок меньше. Давайте рассмотрим два солнечных затмения, которые я уже рассматривал в [16], с полученными нами теориями Земли и Луны. При этом, параметры затмений приведенные в [16] для современных теорий New0 и JPL0 немного изменятся, т.к. теперь я буду учитывать и периодические возмущения для Земли, а также для JPL0 учту периодические возмущения Луны для эллиптической орбиты, а не буду брать как и для New0 из подпрограммы MINI_MOON, где координаты и возмущения рассчитываются для круговой орбиты по упрощенной теории Брауна. Таким образом у меня теперь будут теории New1 и JPL1. Данные по этим двум затмениям, куда я добавил и данные по полученной мною теории Ser1+ и по таблицам Птолемея я привожу в таблицах 10 и 11. А на рис. 27 Вы видите расчет затмения -135 года по моей теории Ser1+ для момента времени за две минуты до окончания затмения и траекторию движения диска Луны относительно Солнца.

 

 

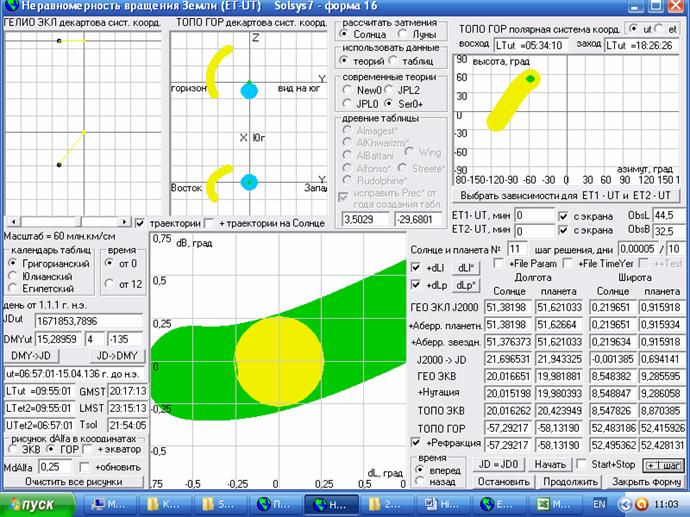
Рис. 27. Расчет солнечного затмения наблюдавшегося 15.4.-135 года в Вавилоне по теории Ser1+. Скриншот программы Solsys7.

 

Таблица 10. Параметры солнечного затмения 29.03.2006 года наблюдавшегося в п. Кировский Астраханской области (долгота 48,153 в.д., широта 45,874 с.ш.) и полученные по таблицам Птолемея и по современным теориям. Для теорий JPL2, JPL1 и New1 эфемеридные поправки рассчитаны по кусочной аппроксимации экспериментальных данных последнего времени, а для таблиц Птолемея подобраны опытным путем. Время дано всемирное (Гринвич) солнечное, а данные Птолемея приведены с исправленной прецессией и выполнены на 11.12.2754 года по Египетскому календарю.

 

Название таблиц, теорий	Фаза в %	Восход	Начало	Начало полного	Конец	Итого
Наблюдаемые данные	100	05:47	10:13	11:23	12:36	02:23
JPL0              ET-UT=1,3	60	05:47	07:52	08:58	10:14	02:22
JPL1              ET-UT=1,3	97	05:47	09:49	11:01	12:10	02:21
JPL2              ET-UT=1,3	100	05:47	10:12	11:23	12:33	02:21
New1             ET-UT=1,3	95	05:47	09:51	11:03	12:11	02:20
Ser1+             ET-UT=0	97	05:47	09:50	11:03	12:11	02:21
Almagest*     ET-UT=0	60	05:44	12:24	13:21	14:20	01:56
Almagest*     ET-UT=100	75	05:44	10:11	11:22	12:29	02:18
Almagest*     ET-UT=183	100	05:44	08:14	09:30	10:47	02:33

 

Таблица 11. Параметры солнечного затмения 15.04.-135 года наблюдавшегося в Вавилоне (долгота 44,5 в.д., широта 32,5 с.ш.) и полученные по современным теориям и по таблицам Птолемея. Для современных теорий эфемеридные поправки рассчитаны как по формуле Далмау, так и по формуле Джонса (в минутах). Время дано местное (Вавилон) солнечное. Данные по таблицам Птолемея приведены с исправленной прецессией и выполнены на 21.07.612 года по Египетскому календарю.

 

Название таблиц, теорий	Фаза в %	Восход	Начало	Начало полного	Конец	Итого
Наблюдаемые данные	100	05:34	07:10	08:22	09:30	02:20
JPL1    ET-UT=0	-5	05:33	-	15:21	-	-
JPL1    ET-UT=182,5  Джонс	70	05:34	09:33	10:45	12:01	02:28
JPL1    ET-UT=196,5  Далмау	75	05:34	09:14	10:29	11:43	02:29
New1    ET-UT=0	-60	05:33	-	14:40	-	-
New1    ET-UT=182,5  Джонс	40	05:34	09:38	10:25	11:10	01:38
New1    ET-UT=196,5  Далмау	60	05:34	09:16	10:06	10:56	01:40
Ser1+                   ET-UT=0	100	05:34	07:41	08:45	09:57	02:16
Almagest*            ET-UT=0	99	05:31	07:08	08:14	09:24	02:16

 

Как видим современные теории при учете периодических возмущений удовлетворительно описывают современные затмения, но без наличия эфемеридной поправки совершенно отказываются описывать затмения давно минувших дней. У них получается фаза затмения -5% и -60%, т.е. это не процент перекрытия диском Луны (по диаметру) диска Солнца, а наоборот процент в диаметрах Солнца, от расстояния на которое диск Луны не дошел до диска Солнца и время указано для момента, когда он максимально приблизился к Солнцу. Подбором эфемеридной поправки можно добиться или того, что совпадет время начала затмения или мы получим фазу затмения 100%, как мы это сделали для таблиц Птолемея для современного затмения, но совпадения и времени и 100% фазы удастся добиться в единичных случаях. Объясняется это и неточностью самих теорий и принципиально не правильным подходом для определения эфемеридной поправки, которую я считаю нужным разделить на две поправки. Подробно об эфемеридных поправках я писал в первой статье этого цикла и по этому останавливаться на этом не буду. Повторюсь только еще раз, что рассчитывать эфемеридную поправку астрономы не могут, а стараются подобрать различные аппроксимации для того, чтобы более менее удачно описать затмения, которые уже наблюдались. Сейчас наиболее известны аппроксимации Джонса и Далмау.

 

Отличительной особенностью моей кинематической теории является то, что для нее не требуется знания эфемеридной поправки, т.к. время для расчета подставляется в нее солнечное (UT), т.е. отсутствует субъективизм присущий всем современным теориям, полученным с использованием динамической методики создания теорий планет. А результаты полученные по моей теории для этих двух затмений говорят сами за себя. И хотя такая точность для Вавилонского затмения быстрее всего удачное стечение обстоятельств для рассчитанных координат и учтенных поправок от периодических возмущений, но даже, если бы у меня получилась фаза затмения 90% это тоже бы было подтверждением работоспособности полученной мною кинематической теории планет. Однако я рано заявил о полученной теории планет, т.к. мы еще не сделали теорию для Меркурия, Венеры и Марса. Вот этим сейчас и займемся, а начнем с Меркурия, у которого также как и раньше для Солнца и Луны разобъем выборку данных наблюдений из файла SUMM1_G_200 на отдельные интервалы (опыты).

 

Таблица 12. Интервалы опытов для обработки данных наблюдений за Меркурием.

1	1837-1886 / 1422	1837-1870 / 899
2	1887-1932 / 2776	1871-1905 / 1032
3	1933-1982 / 3288	1906-1924 / 1153
4		1925-1937 / 1778
5		1938-1950 / 1369
6		1951-1972 / 879
7		1974-1982 / 376

 

Но прежде чем приступить к обработке данных из файла SUMM1_G_200 мы его отбракуем по теории JPL0 по критерию dR<26 тыс.км. и получим файл SUMM1_G_200LB. Теперь по этому файлу найдем периодические возмущения для Меркурия, когда его координаты рассчитываются по теории JPL0 (см. рис. 14), а затем уже с учетом периодических возмущений еще раз отбракуем данные в файле SUMM1_G_200 по критерию dR<26 тыс.км. и получим файл SUMM1_G_201LB (позже повторная отбраковка для Меркурия, Венеры и Марса будет идти с периодическими возмущениями по табл. 6 и по теории Ser00 для этих планет). При этом, для определения координат Земли будем использовать уже полученную теорию Ser. Теперь оптимизируем параметры орбиты Меркурия по критерию dR, но при разных вариантах большой полуоси R Меркурия и Земли, т.к. с этим параметром в теории Земли у нас были проблемы и я хочу посмотреть насколько сильно различные значения R как Земли, так и Меркурия повлияют на остальные параметры. При этом в таблице 13, если не оговорено особо (около номера плана) кругом использовалась теория Земли Ser (кроме плана 191). При этом, в планах 181...185 Ser00 и в планах 1851...1861 Ser0, а в планах 181 и 191 кроме этого и размер большой полуоси Меркурия R1 не оптимизировался, а задавался по теории JPL0. Что касается параметров AlfaP, AlfaU, Betta, Eks и AlfaL, то я сразу приведу зависимости для их расчета, получившиеся у меня по плану 1851, а вот с параметрами Wsr и R будем разбираться отдельно.

 

Таблица 13. Вековые смещения параметров орбиты Меркурия, полученные на программе Solsys7 при обработке данных оптических наблюдений при различных вариантах теории Земли и значений большой полуоси орбиты Меркурия R1. При выполнении всех планов использовался файл 201LB , критерий оптимизации кругом dR и учитывались периодические возмущения. В планах 18Х использовалась теория Земли Ser, а в плане 191 – JPL.

планы	dAlfaP	dAlfaU	dBetta	dEks	dW	dR
191=7R    R1=JPL0	570,0          +/-6,1	-434,3           +/-10,3	-19,94        +/-0,43	16,60          +/-4,40	31+/-350	63+/-3*
181=7R    R1,R3=JPL0	578,5          +/-6,5	-433,6        +/-8,4	-19,96        +/-0,50	21,68          +/-4,26	190+/-350	63+/-3*
182 = 7R    R3=JPL0	577,9         +/-7,0	-433,9          +/-8,3	-19,90         +/-0,50	20,30           +/-3,90	190+/-340	240+/-300
185=7R    R3=Ser00	578,0          +/-7,2	-433,2        +/-8,6	-19,91        +/-0,50	20,63          +/-3,93	208+/-373	-85+/-300
1851=7R      R3=Ser0	578,0          +/-7,3	-433,2           +/-8,2	-19,84         +/-0,51	20,10          +/-3,98	208+/-382	-92+/-297
1852=7R    R3=Ser0	578,0          +/-7,4	-433,1           +/-8,4	-19,83        +/-0,51	19,86          +/-3,95	214+/-376	-87+/-295
1861=3R    R3=Ser0	572,4          +/-20,3	-428,3           +/-0,84	-20,01        +/-0,26	21,57          +/-3,02	408+/-4	-94+/-505

* - параметр не оптимизировался

 

Рис.28. Изменение параметров AlfaP1 и AlfaU1 по плану 1851. Скриншоты программы Solsys7.

 

Рис.29. Изменение параметров Betta1 и Eks1 по плану 1851. Скриншоты программы Solsys7.

 

AlfaP1 = 77,457563 + 0,160566 * dT

AlfaU1 = 48,335022 – 0,120320 * dT

Betta1 = 7,005067 – 0,00551068 * dT

Eks1 = 0,205636 + 0,0000201028 * dT

AlfaL1 = 252,253944 + 149472,674747 * dT

 

Теперь давайте аналогичным образом обработаем данные наблюдений за Венерой и Марсом, а потом проанализируем полученные данные сразу для трех планет.  Разбиваем выборку данных наблюдений за Венерой из файла SUMM2_G_200 на отдельные интервалы (табл. 14). Отбраковываем наблюдения в нем по теории JPL0 по критерию dR<18 тыс.км. и получаем файл SUMM2_G_200LB. Теперь по этому файлу найдем периодические возмущения для Венеры, когда ее координаты рассчитываются по теории JPL0 (см. рис. 14), а затем уже с учетом периодических возмущений еще раз отбракуем данные в файле SUMM2_G_200 по критерию dR<10 тыс.км. и получаем файл SUMM2_G_201LB. При этом, для определения координат Земли будем использовать уже полученную теорию Ser. Теперь оптимизируем параметры орбиты Венеры по критерию dR, но при разных вариантах большой полуоси R Венеры и Земли . При этом в таблице 15, если не оговорено особо (около номера плана) кругом использовалась теория Земли Ser (кроме плана 191). При этом, в планах 281...285 Ser00 и в планах 2851...2861 Ser0, а в планах 281 и 291 кроме этого и размер большой полуоси Венеры R2 не оптимизировался, а задавался по теории JPL0. 

 

 

 

 

Таблица 14. Интервалы опытов для обработки данных наблюдений за Венерой.

1	1800-1860 / 1865	1800-1828 / 334
2	1861-1921 / 5927	1836-1860 / 1531
3	1922-1982 / 7280	1861-1877 / 1516
4		1878-1896 / 1698
5		1897-1919 / 2582
6		1920-1940 / 3376
7		1941-1960 / 2687
8		1961-1982 / 1348

 

Таблица 15. Вековые смещения параметров орбиты Венеры, полученные на программе Solsys7 при обработке данных оптических наблюдений при различных вариантах теории Земли и значений большой полуоси орбиты Венеры (R2). При выполнении всех планов использовался файл 201LB , критерий оптимизации кругом dR и учитывались периодические возмущения. В планах 28Х использовалась теория Земли Ser, а в плане 291 - JPL.

планы	dAlfaP	dAlfaU	dBetta	dEks	dW	dR
291=8R    R2=JPL0	33,0          +/-105,2	-1000,4           +/-7,4	-3,18           +/-0,27	-50,6          +/-1,4	21+/-190	590+/-14*
281=8R    R2,R3=JPL0	-1,3          +/-77,2	-997,3           +/-6,5	-2,90           +/-0,22	-44,6          +/-3,1	67+/-180	590+/-14*
282=8R      R3=JPL0	-6,2          +/-81,6	-997,0           +/-6,4	-2,85           +/-0,24	-44,4          +/-3,1	68+/-170	14+/-520
285=8R    R3=Ser00	-5,9          +/-82,7	-997,1           +/-7,0	-2,85           +/-0,24	-44,4          +/-3,0	64+/-180	-604+/-517
2851=8R      R3=Ser0	30,3          +/-83,5	-996,5           +/-6,8	-2,83           +/-0,21	-45,3            +/-2,9	66+/-168	-549+/-365
2861=3R    R3=Ser0	-12,9         +/-46,9	-968,5           +/-6,5	-2,81           +/-0,29	-47,2          +/-1,7	43+/-5	-738+/-269

* - параметр не оптимизировался

 

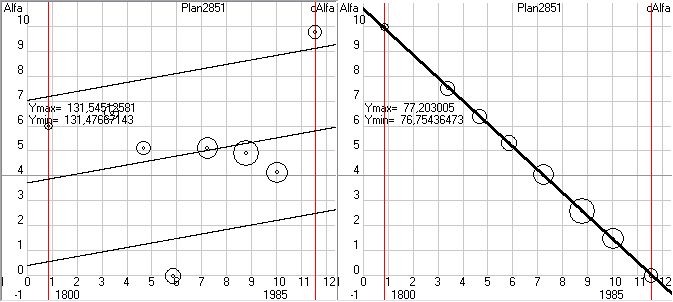
Рис.30. Изменение параметров AlfaP2 и AlfaU2 по плану 2851. Скриншоты программы Solsys7.

 

 

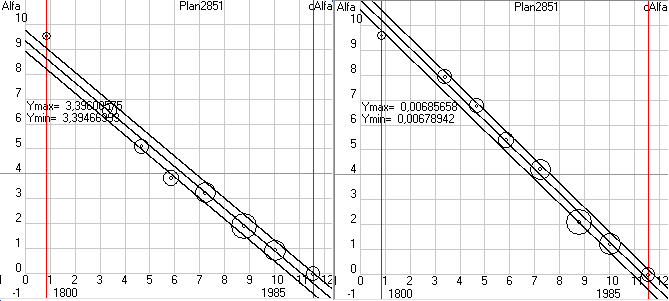
Рис.31. Изменение параметров Betta2 и Eks2 по плану 2851. Скриншоты программы Solsys7.

 

AlfaP2 = 131,519558 + 0,00843485 * dT

AlfaU2 = 76,682467 – 0,276804 * dT

Betta2 = 3,394406 – 0,000785760 * dT

Eks2 = 0,00677596 – 0,0000453236 * dT

AlfaL2 = 181,979394 + 58517,814964 * dT

 

Для Марса также разбиваем выборку данных наблюдений из файла SUMM4_G_200 на отдельные интервалы (табл. 16).  Отбраковываем данные из файла SUMM4_G_200 по теории JPL0 по критерию dR<80 тыс.км. и получим файл SUMM4_G_200LB. Теперь по этому файлу найдем периодические возмущения для Марса, когда его координаты рассчитываются по теории JPL0 (см. рис. 14), а затем уже с учетом периодических возмущений еще раз отбракуем данные в файле SUMM4_G_200 по критерию dR<40 тыс.км. и получаем файл SUMM4_G_201LB. При этом, для определения координат Земли будем использовать уже полученную теорию Ser. Теперь оптимизируем параметры орбиты Марса по критерию dR, но при разных вариантах большой полуоси R Марса и Земли.  При этом в таблице 17, если не оговорено особо (около номера плана) кругом использовалась теория Земли Ser (кроме плана 491). При этом, в планах 481...485 Ser00 и в планах 4851...4862 Ser0, а в планах 481 и 491 кроме этого и размер большой полуоси Марса R4 не оптимизировался, а задавался по теории JPL0. 

 

 

Таблица 16. Интервалы опытов для обработки данных наблюдений за Марсом.

1	1835-1884 / 1904	1751...1821 / 291	1751-1799 / 165
2	1885-1933 / 1033	1822...1861 / 1206	1800-1834 / 306
3	1934-1993 / 1696	1862...1902 / 1273	1835-1864 / 1187
4		1903...1943 / 882	1865-1900 / 1135
5		1944...1993 / 1388	1901-1930 / 550
6			1931-1960 / 738
7			1961-1993 / 1023

 

 

Таблица 17. Вековые смещения параметров орбиты Марса, полученные на программе Solsys7 при обработке данных оптических наблюдений при различных вариантах теории Земли и значений большой полуоси орбиты Марса (R4). При выполнении всех планов использовался файл 201LB, критерий оптимизации кругом dR и учитывались периодические возмущения. В планах 48Х использовалась теория Земли Ser, а в плане 491 - JPL.

планы	dAlfaP	dAlfaU	dBetta	dEks	dW	dR
491=7R    R4=JPL0	1585,0          +/-25,5	-1046,4           +/-29,6	-29,50        +/-0,89	99,3 +/-10,9	-160+/-370	2800 +/-140*
481=7R    R4,R3=JPL0	1586,0          +/-23,4	-1032,1           +/-29,2	-29,51        +/-0,84	98,7 +/-10,9	-170+/-381	2800 +/-140*
482=7R      R3=JPL0	1581,8          +/-17,4	-1033,2         +/-27,5	-29,30        +/-1,10	96,3 +/-11,3	-200+/-310	6300 +/-18000
485    R3=Ser00	1583,4          +/-15,4	-1030,6           +/-28,4	-29,28        +/-0,92	95,9          +/-12,0	-185+/-288	+4995        +/-17381
4851=7R    R3=Ser0	1582,7          +/-30,2	-1028,0           +/-29,9	-29,39        +/-0,85	95,5          +/-12,4	-291+/-395	+4253        +/-19249
4861=3R    R3=Ser0	1621,2          +/-13,1	-1058,6           +/-7,0	-31,37        +/-0,33	109,4        +/-3,71	-776+/-170	-8734         +/-8155
4862=5R    R3=Ser0	1589,9          +/-16,6	-1037,6           +/-6,8	-29,24        +/-0,86	87,19        +/-8,10	77+/-215	-6029         +/-8443

* - параметр не оптимизировался

 

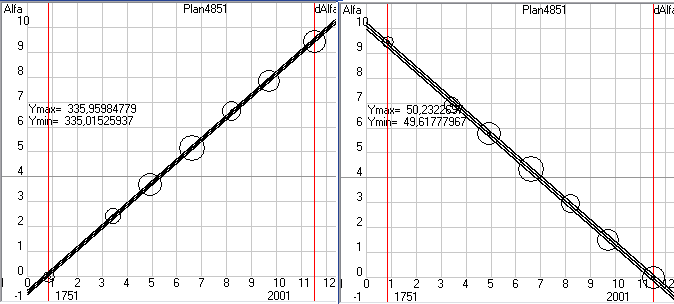
Рис.32. Изменение параметров AlfaP4 и AlfaU4 по плану 4851. Скриншоты программы Solsys7.

 

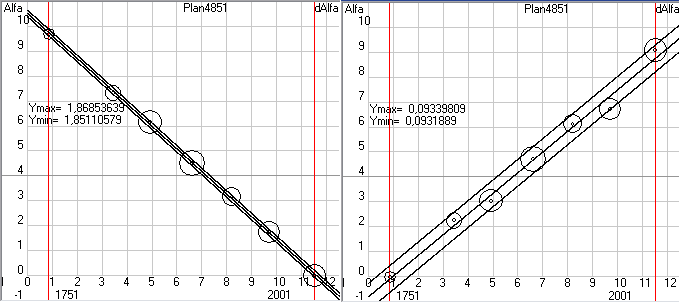
Рис.33. Изменение параметров Betta4 и  Eks4 по плану 4851. Скриншоты программы Solsys7.

 

AlfaP4 = 336,045866 + 0,439650 * dT

AlfaU4 = 49,563453 – 0,285561 * dT

Betta4 = 1,849726 – 0,00816419 * dT

Eks4 = 0,0934080 + 0,0000955278 * dT

AlfaL4 = -4,553420 + 19140,305921 * dT

 

Теперь поподробнее остановимся на изменение для этих планет таких параметров как Wsr и R. Как мы видим, доверительные интервалы по этим параметрам в планах Х851 получились очень большие и позволяют судить только о качественном изменение этих параметров. Дальнейшее увеличение точности оптимизации параметров до одной тысячной интервала варьирования параметра (см. план 1852, где к тому же я в обязательном порядке применил ортогональный план, который лучше подходит для описания самой области оптимума) ни к каким заметным изменениям не привело. Тогда я решил попробовать длинные опыты, как я это делал для Wsr Земли и когда для средних по продолжительности интервала опытов удалось уменьшить дисперсию, т.е. доверительные интервалы оптимальных параметров. Действительно, для Меркурия и Венеры с формальной точки зрения получились отличные данные по Wsr, а Марсу это не помогло. Я даже выполнил для него план со средними продолжительностями опытов (4862), но доверительные интервалы оставались очень большими. Более того, я получил не уменьшение Wsr со временем, как во всех предыдущих планах, а увеличение. А объясняется различное влияние увеличения продолжительности опытов на полученные доверительные интервалы у Меркурия и Венеры с одной стороны и Марса с другой стороны разными краевыми эффектами в этих опытах и на рис. 34 мы это видим по изменению критерия dR в длинных опытах этих планет.

 

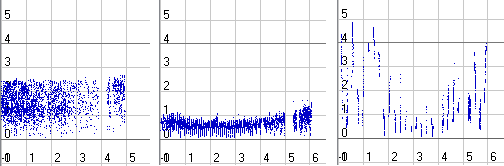
Рис. 34. Отклонение наблюдательных данных от расчетных по критерию dR в опытах №3 планов Х861 у Меркурия, Венеры и Марса. Масштаб по оси абсцисс 10 лет/см, а по оси ординат 10 угл.сек./см для Меркурия и Венеры и 20 угл.сек./см для Марса. Скриншоты программы Solsys7.

 

У Меркурия краевой эффект почти не проявляется (правда у него и продолжительность опыта всего 50 лет), у Венеры проявляется в средней форме, а у Марса он очень заметен. По этому никакого уменьшения доверительных интервалов у Марса от увеличения продолжительности опытов мы и не наблюдаем. Но и обольщаться по поводу просто отличных результатов по Wsr у Меркурия и Венеры особо не стоит, хотя данные плана 1861 просто не могут не радовать (см. рис. 35). Дело в том, что как бы не было мало влияние краевых эффектов на точность оптимизации параметров, но оно присутствует, а такие параметры как Wsr и особенно R ввиду их очень медленного изменения со временем очень чувствительны к малейшим неточностям. Вот если бы у нас появилась такая красивая прямая минимум по 5-и опытам, то тогда можно бы было быть уверенным в точности полученных результатов. А для этого надо увеличивать выборку наблюдательных данных и лучше центрировать данные разных обсерваторий. Но пока у нас есть только сделанная мною выборка наблюдательных данных удовлетворимся пока и этим результатом. А для зависимости изменения Wsr у Марса придется довольствоваться результатами опыта 4851.

 

 

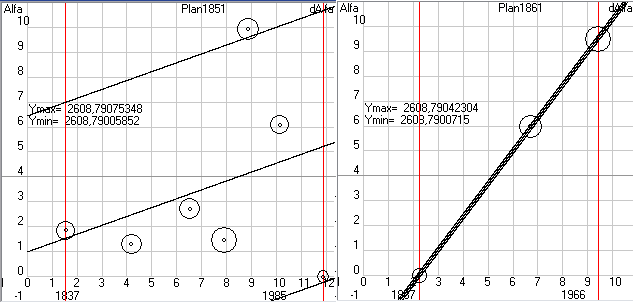
Рис.35. Изменение параметра Wsr у Меркурия по планам 1851 и 1861. Скриншот программы Solsys7.

 

А с параметром R для этих планет результаты у нас получаются еще хуже чем по Wsr. Более того, здесь зависимость изменения R у Земли влияет даже на знак изменения R у этих планет. Так при изменение R3 по теории JPL0 (планы 182 и 282) у Меркурия и Венеры R увеличивалась со временем, а далее при изменение R3 по теории Ser0 у них R стала со временем уменьшаться. А вот у Марса знак изменения R4 при этом остался тот же, но при выполнение длинных и средних опытов (планы 4861 и 4862) он тоже изменился. По этому, определение зависимостей для планет по параметру R непосредственно при обработке данных наблюдений, как мы делали это по остальным параметрам, я считаю нецелесообразным. Более надежным путем определения параметра R для планет я считаю расчетный вариант через изменение Wsr этих планет, т.е. так, как мы определяли изменение R для Земли. По этому, рассчитаем по полученным зависимостям Wsr ее значение через 10 млн. лет и по формуле (6) рассчитаем значение R для этого времени и на стандартную эпоху J2000, а затем по разнице двух значений R найдем вековые изменения этого параметра. И хотя при этом мы найдем изменение радиуса круговой орбиты планет, а не величины большой полуоси, но другого пути я пока не вижу. Изменения средней угловой скорости планет по данным планов, которые приведены в скобках, будут следующие.

 

Wsr1(1861) = 2608,790628 + 0,000408236 * dT

Wsr2(2861) = 1021,328625 + 0,0000425817 * dT

Wsr4(4851) = 334,061253 - 0,000290187 * dT

 

Здесь первая цифра это значение Wsr на эпоху J2000, а через 10 млн. лет значения будут такие

 

Wsr1(+10) = 2608,790628 + 40,8236 = 2649,614228 (рад/век)

Wsr2(+10) = 1021,328625 + 4,25817 = 1025,586795 (рад/век)

Wsr4(+10) = 334,061253 - 29,0187 = 305,042553 (рад/век)

 

Далее переводим эти угловые скорости в размерность (рад/с) и подставляем в формулу (6) для расчета радиусов круговых орбит, где gamma * m0 = 13,276853 * 10^19 (н * м^2 / кг)

 

R1(2000) = (13,276853 / (8,266759)^2)^0,333 * 10^11 = 0,57917285 * 10^11 (м)

R1(+10) = (13,276853 / (8,396121)^2)^0,333 * 10^11 = 0,57320846 * 10^11 (м)

R2(2000) = (13,276853 / (3,236395)^2)^0,333 * 10^11 = 1,08224113 * 10^11 (м)

R2(+10) = (13,276853 / (3,249888)^2)^0,333 * 10^11 = 1,07924353 * 10^11 (м)

R4(2000) = (13,276853 / (1,058576)^2)^0,333 * 10^11 = 2,27973143 * 10^11 (м)

R4(+10) = (13,276853 / (0,966622)^2)^0,333 * 10^11 = 2,42211037 * 10^11 (м)

 

Теперь находим изменение радиусов круговых орбит за 10 млн. лет, т.е. за 100000 веков, а потом вековые изменения этих радиусов и записываем их изменение в функции времени, а рядом для сравнения записываем эти изменения полученные нами по планам при прямой оптимизации этих параметров

 

R1= 57917,285 – 0,00596439 * dT

R1(1851)  = 57916,304570 – 0,0918895 * dT

R2= 108224,113 – 0,0029976 * dT

R2(2851)  = 108225,876437 – 0,548388 * dT

R4= 227973,143 + 0,142379 * dT

R4(4851)  = 227970,660074 + 4,254787 * dT

 

Да, желательно бы было получить такие изменения R, чтобы значения в обоих формулах совпали, но для этого, во-первых, надо уточнить зависимость изменения R для Земли, а для этого опять таки надо увеличивать выборку наблюдательных данных и более тщательно центрировать данные наблюдений в этой выборке. Но эту работу теперь может выполнить каждый кто прочитал эту статью, а помогут ему в этом мои программы Solsys7 и ObsData3, которые я выложу в интернете после того как закончу описание этих программ. А проверить насколько качественно мы определили параметры орбиты Венеры мы можем прямо сейчас, рассмотрев транзит Венеры по диску Солнца, который я рассматривал в предыдущей статье. Для этого я дополню данные в таблице, которую я приводил в [16], данными по созданной мною теории Ser1и учту периодические возмущения в теориях JPL0 и New0.

 

Таблица 18. Наблюдаемые и расчетные данные транзита Венеры по диску Солнца 8.6.2004 года (наблюдаемые данные по всемирному времени UT взяты здесь http://www.venus2004.org/fr/galerie.php    http://www.venus2004.org/comprendre/d/dossier432-1.php?langue=2        http://eclipse.astronomie.info/transit/venus , расчетные данные в топоцентрических экваториальных координатах получены при наблюдение из точки с координатами ObsL=15 и ObsB=50 градусов).

Название таблиц, теорий	Начало	Конец	Итого
Наблюдаемые данные	05:20	11:23	06:03
JPL2                  ET-UT=1,2	05:21	11:21	06:00
JPL1                  ET-UT=1,2	05:21	11:21	06:00
New1                ET-UT=1,2	05:23	11:24	06:01
Ser1                   ET-UT=0	05:24	11:25	06:01

 

Учитывая, что данные наблюдений мы обрабатывали по одной методике, можно и без проверки быть уверенным в том, что и для Меркурия и для Марса у нас тоже получилась удовлетворительная теория Ser0, а с учетом части периодических возмущений от других планет и теория Ser1. Теперь давайте попробуем уточнить теорию Ser0 для Меркурия, Венеры и Марса с учетом данных таблиц древних астрономов и получим теорию Ser0+. Для этого точно также, как мы это делали для Земли и Луны, будем по плану задавать различные параметры орбит этих планет и оптимизировать их по минимальному отклонению по расстоянию dRpl. Только теперь мы уже будем задавать координаты Земли, с которой наблюдаем за этими планетами, по полученной нами теории Ser0+. К сожалению вынужден констатировать, что полученные по таблицах древних астрономов параметры орбит этих планет не позволят нам сделать для них теорию Ser0+, т.к. данные получились очень противоречивые. Причем средние отклонения по расстоянию (в таблицах ниже они даны в тыс.км.) при оптимизации получались очень большие и только благодаря мощи метода многофакторного планирования удалось вытащить из таблиц хоть какие то результаты. А из Альфонсовых таблиц для Меркурия вообще не удалось вытащить параметры его орбиты. Сейчас я понял в чем была ошибка. Надо было положения Земли для геоцентрических таблиц определять тоже по таблицам (находить положение Солнца, а затем по нему определять положение Земли). Да и для гелиоцентрических таблиц надо бы было делать также.

 

Дело в том, что удовлетворительные данные по таблицам для положения планет Меркурия, Венеры и Марса получаются только для тех положений Земли, которые заложили авторы таблиц в свои теории. Особенно это наглядно проявляется для Меркурия и Венеры в геоцентрических таблицах, где их положение определяется относительно Солнца, когда Солнце движется вокруг Земли. И когда я по своей теории Ser0+ определяю положение Солнца относительно Земли не там, где оно получается по таблицам, то и все положения планет определяются с этой систематической ошибкой. Но пересчитывать сейчас, получившиеся у меня параметры орбит Меркурия, Венеры и Марса я не буду. Связано это с тем, что для этого надо существенно переделывать код программы Solsys7, а я уже выкладываю тексты статей в интернете со ссылками на эту программу, но сам пока никак не могу сделать описание уже существующего рабочего кода программы Solsys7, чтобы выложить ее в интернете. По этому, я возможно еще вернусь к этому вопросу, но значительно позже, т.е. когда найду скорость гравитации, т.к. теория Ser0+ мне будет нужна только в этом случае. А сейчас я просто приведу получившиеся у меня по таблицам параметры орбит Меркурия, Венеры и Марса (табл. 19, 20, 21), где в последней строчке для сравнения я дам параметры орбит по теории Ser0 на эпоху J2000. А ввиду того, что я пока не буду уточнять теорию Ser0 по этим планетам, когда мы на форме 16 будем отмечать переключатель Ser0+, то координаты Меркурия, Венеры и Марса будут пока рассчитываться по теории Ser0.   

 

Таблица 19. Параметры орбиты Меркурия полученные мною при обработке данных из таблиц древних астрономов и данные по теории Ser0 на эпоху J2000.

 

данные наблюдений	dR	вес	AlfaP	AlfaU	Betta	Eks	Wsr
Almagest -141...-112	2845,8	0,0004	61,893	33,282	6,899	0,1247	2608,775
AlKhwarizmi 800...829	3669,6	0,0003	74,497	45,155	12,785	0,1462	2608,775
AlBattani 900...929	2786,8	0,0004	61,347	32,750	6,825	0,1154	2608,770
Alfonso 1252...1281	-	-	-	-	-	-	-
Rudolphine 1620...1649	84,5	0,0118	78,391	47,745	6,966	0,2071	2608,795
Streete 1620...1649	84,7	0,0118	76,892	48,521	6,931	0,2066	2608,788
Wing 1640...1669	75,0	0,0133	76,211	48,381	6,945	0,2071	2608,796
Ser0          J2000	-	-	77,458	48,335	7,005	0,2056	2608,791

 

 

Таблица 20. Параметры орбиты Венеры полученные мною при обработке данных из таблиц древних астрономов и данные по теории Ser0 на эпоху J2000.

 

данные наблюдений	dR	вес	AlfaP	AlfaU	Betta	Eks	Wsr
Almagest -141...-112	880,5	0,0011	173,465	76,769	2,894	0,00592	1076,663
AlKhwarizmi 800...829	533,5	0,0019	81,328	77,603	5,031	0,00012	1100,279
AlBattani 900...929	650,9	0,0015	271,859	95,346	2,817	-0,00042	1076,915
Alfonso 1252...1281	1080,8	0,0009	222,613	25,227	0,089	0,00022	1080,882
Rudolphine 1620...1649	125,7	0,0080	134,422	77,745	3,364	0,00515	1083,311
Streete 1620...1649	75,1	0,0133	131,031	77,629	3,381	0,00615	1082,090
Wing 1640...1669	84,9	0,0118	131,269	77,926	3,362	0,00579	1083,127
Ser0          J2000	-	-	131,520	76,683	3,394	0,00678	1021,329

 

 

Таблица 21. Параметры орбиты Марса полученные мною при обработке данных из таблиц древних астрономов и данные по теории Ser0 на эпоху J2000.

 

данные наблюдений	dR	вес	AlfaP	AlfaU	Betta	Eks	Wsr
Almagest -141...-112	3031,8	0,0003	327,830	29,849	0,529	0,09246	334,0551
AlKhwarizmi 800...829	4104,3	0,0002	333,465	39,884	2,688	0,08857	334,0441
AlBattani 900...929	1901,3	0,0005	326,580	45,579	1,091	0,09303	334,0701
Alfonso 1252...1281	7183,2	0,0001	325,789	49,637	0,041	0,08681	334,0131
Rudolphine 1620...1649	75,5	0,0133	334,358	51,004	1,880	0,09294	334,0609
Streete 1620...1649	37,2	0,0267	334,250	51,113	1,892	0,09280	334,0615
Wing 1640...1669	62,4	0,0160	334,598	51,057	1,874	0,09288	334,0598
Ser0          J2000	-	-	336,046	49,563	1,850	0,09341	334,0613

 

Но не смотря на неудачу по созданию теории Ser0+, главную задачу в этом исследование, т.е. нахождение наблюдаемых вековых смещений параметров орбит за последние 200 лет по теории Ser0, мы выполнили. Да, полученные мною значения вековых смещений (см. табл. 21) немного отличаются от смещений заложенных в известные современные теории планет, но я больше доверяю своим значениям, а не полученным с использованием современной методики создания теорий планет. По этому, при поиске скорости гравитации я буду пользоваться своими значениями смещений, а что из этого получится надеюсь мы увидим через год. А пока можете просто сравнить вековые смещения параметров орбит заложенные в известные современные теории и полученные мною, а также сравнить их со смещениями, которые получаются при использование моделей с системой масс планет принятой в JPL, когда в этих моделях используется классический закон притяжения Ньютона и с поправкой Холла. При этом смещения заложенные в современные теории и получающиеся на моделях я получил обрабатывая рассчитанные по этим теориям положения планет по методике, которую я изложу в следующей статье. Как Вы заметили, все эти теории в таблице названы имитаторами, т.к. они являются аппроксимациями данных полученных на моделях. И даже эфемериды DE405 (JPL2), хотя и с очень высокой точностью повторяют данные полученные при моделирование Солнечной системы сотрудниками JPL, но это все же аппроксимация, а не сама модель. И маленькое пояснение. Теорию Ньюкома New0 я использовал не оригинальную, а ее современную трактовку, изложенную в [11], а теорию APC2 я взял из [15] .

 

Таблица 22. Вековые смещения параметров орбит, полученные на программах Solsys6 и Solsys7 с использованием данных полученных по имитаторам (астрономическим теориям) Солнечной системы New0, APC2 и JPL2 и данным математических моделей Солнечной системы, а также полученных при обработке непосредственно данных оптических наблюдений для создания кинематической астрономической теории Ser0. Смещения углов даны в угловых секундах, а смещение эксцентриситета в безразмерных единицах и увеличено в 10^6 раз. Доверительная вероятность (надежность) данных 95%.

параметры	имитаторы				модели
	New0	APC2	JPL2	Ser0	/R^2	/R^n*
dAlfaP1 dAlfaU1 dBetta1 dEks1	+570,73 -452,18 -21,43 +20,55	+574,02 -450,34 -21,44 +20,52	+572,20 -449,95 -21,44 +20,50	+578,0 -433,2 -19,84 +20,10	+529,59 -450,36 -21,455 +20,421	+573,41 -450,40 -21,457 +20,417
dAlfaP2 dAlfaU2 dBetta2 dEks2	+54,41 -999,86 -2,51 -48,01	+59,12 -1011,65 -2,42 -48,20	+43,64     -998,36 -2,52  -48,43	+30,3 -996,5 -2,83 -45,33	+45,555 -999,08 -2,521 -49,417	+61,193 -999,06 -2,521 -49,409
dAlfaP3 dAlfaU3 dBetta3 dEks3	+1160,37 -869,85 -47,19 -41,33	+1185,68 -872,74 -47,14 -41,62	+1158,55 -861,63 -47,17 -41,93	+1141,6 -868,0 -47,45 -41,57	+1141,97 -845,52 -47,235 -43,291	+1152,56 -845,36 -47,234 -43,291
dAlfaP4 dAlfaU4 dBetta4 dEks4	+1601,09 -1054,74 -29,11 +92,27	+1599,64 -1058,58 -29,16 +92,07	+1600,02 -1050,49      -28,93 +91,63	+1582,7          -1028,0        -29,39           +95,53	+1598,09 -1052,79 -29,025 +96,255	+1603,70 -1052,77 -29,025 +96,252

 

* - показатель степени n во второй модели в формуле Ньютона F=G*m*M/R^n брался таким, каким он был у Ньюкома, т.е. n=2,0000001612 (у Холла было n=2,0000001574).

 

 

 

 

 

                                                            Список литературы

 

1. - К.Птолемей //Альмагест или математическое сочинение в тринадцати книгах// http://naturalhistory.narod.ru/Person/Antic/Ptolemey/Almag_ogl.htm 

http://hbar.phys.msu.ru/gorm/almagest/text/book.htm 

2. – Кеплеровы элементы орбит с 1800 по 2050годы  http://ssd.jpl.nasa.gov/txt/p_elem_t1.txt

3.- Кеплеровы элементы орбит с -3000 по 3000 годы http://ssd.jpl.nasa.gov/txt/p_elem_t2.txt

4.- E. Myles Standish and James G. Williams. Orbital Ephemerides of the Sun, Moon, and Planets http://iau-comm4.jpl.nasa.gov/XSChap8.pdf  

5. - Е.Майлс Стэндиш, Джеймс Г.Вильямс. Орбитальные эфемериды Солнца, Луны и планет  (в переводе Вадима Чазова http://vadimchazov.narod.ru/text_htm/xsru00.htm  )

6. – S. Newcomb //Four inner planets and the fundamental constants of astronomy// - Washington, Goverment printing office, 1895, 202 p.

7. – М.Ф.Субботин //Введение в теоретическую астрономию// - М.: Наука, 1968, 800 с.

8. – Карим Хайдаров //Эфир великий часовщик// http://www.bourabai.kz/watchmaker.htm

9. – Н.Т.Роузвер //Перигелий Меркурия. От Леверье до Эйнштейна//: пер. с англ. – М.: Мир, 1985. – 246 с.

10. – О.В.Зайцев //Принцип Маха и орбитальная прецессия планет //                           http://www.physical-congress.spb.ru/russian/pmoop/pmoop.asp#_Toc479550256

11. - Справочное руководство по небесной механике и астродинамике, под редакцией Г.Н. Дубошина, издание второе, дополненное и переработанное - М.: Наука, 1976. – 864 с.

12. – Jean Meeus //Matematical astronomy morsels// Richmond: Willmann-Bell Inc., 1977, 379 p.

13. -  С.В.Мельников, В.Р.Алешкин, П.М.Рощин //Планирование эксперимента в исследованиях сельскохозяйственных процессов// Л.: Колос, 1980, 168 с.

14 – Адлер Ю.П., Маркова Е.В., Грановский Ю.Б. // Планирование экспериментов при поиске оптимальных условий// М.: Наука, 1967, 280 с.

15. - О. Монтенбрук, Т. Пфлегер //Астрономия с персональным компьютером// пер. с нем. М.: Мир, 1993 – 279 с.)

16. – С.Ю.Юдин //О равноденствиях Гиппарха и Птолемея//    (http://modsys.narod.ru/Stat/Stat_Est/Hipp_Ptolo/Hipp_Ptolo2.html ) 2012, 54 с