______Свободно распространяемые программы _____
![]()
___Программы распространяются свободно только для их использования в некоммерческих целях
_______ВНИМАНИЕ
- здесь я
буду размещать программы,
написанные в основном на языке
программирования VisualBasic 6.0, которые
требуют для своей работы
библиотеку MSVBVM60.DLL. По этому, если у
Вас на компьютере установлена
операционная система Windows XP, Windows Vista или Windows 7,
то эта библиотека у Вас уже есть, хотя, если установлена Windows XP,
то там может быть и библиотека MSVBVM50.DLL, т.е. библиотека для
предыдущей версии языка VisualBasic. Если это так (посмотрите в папке C: \ WINDOWS \ SYSTEM32), то Вам
надо будет скачать
библиотеку MSVBVM60.DLL, а затем
поместить ее в папку C: \ WINDOWS \ SYSTEM32 и зарегистрировать.
Потом можете скачивать только исполняемые
файлы нужных Вам программ, например,
Solsys4exe.zip или Solsys5exe.rar и после распаковывания этих архивов
запускать исполняемые файлы как и все остальные
программы. При этом на всякий случай проверьте еще региональные
настройки, т.к. в моих программах для отделения целых чисел от
десятичных используется запятая, т.е. так, как принято в России. А в
тех случаях, когда я
буду выкладывать программы на
других языках программирования, я
буду оговаривать особенности их
работы отдельно. Таким образом,
если у Вас стоят или Windows XP, Windows Vista или Windows 7 (32-х разрядная) следующий абзац можете не читать.
А вот если у Вас установлены версии Windows выше Windows7 или установлена не 32-х разрядная версия этой операционной системы, а 64-х разрядная, то Вам
быстрее всего придется установить
на свой компьютер не только
библиотеку виртуальной машины VisualBasic 6.0, т.е. файл MSVBVM60.DLL, но и некоторые
другие библиотеки. О том, что у Вас нет какой то
библиотеки компьютер Вам сообщит
сам, если программа при запуске не
найдет ее в нужном месте. Все эти
библиотеки (если нужно) Вы
устанавливаете и регистрируете только один раз. При этом, чтобы программы
работали, эти библиотеки даже не
обязательно регистрировать а достаточно только поместить их в ту
папку, где
находится исполняемый файл программы, но лучше, конечно же, их
зарегистрировать, чтобы не помещать их каждый раз в папку с исполняемым
файлом. А в нижеприведенном архиве 11dll.zip я упаковал 11
различных библиотек, которые вам могут понадобиться.
архив различных библиотек 11dll.zip (1,21 Mb)
Естественные науки
Maikelson1 -
программа для моделирования работы интерферометров Майкельсона и моей
конструкции, а также для построения интерференционной картинки с
использованием параметров двух лучей света, падающих на экран, которые
получены при проведении вычислительного эксперимента на математических
моделях установок.
исполняемый и исходные файлы Maikelson.rar - (Windows 95-98-XP-Vista-7, 23,5 Mb)
Galiley1 - программа для проверки различных
принципов относительности, положенных в основу теории относительности.
исполняемый и исходные файлы Galiley1.rar - (Windows 95-98-XP-Vista-7, 0,74 Mb)
________Эта программа, кроме того, что позволяет выполнить
вычислительные эксперименты, как на классических, так и на релятивистских
математических моделях различных систем, для экспериментальной проверки наличия
в природе принципа относительности (ПО) наблюдателей объекта (в формулировке
Эйнштейна, которая отличается от формулировки Галилея и Ньютона для их ПО,
которые у них являются принципами эквивалентности условий проведения
эксперимента), позволяет так же рассмотреть и другие вопросы, отраженные как в
специальной (СТО), так и общей (ОТО) теориях относительности. Например, на
форме 10 (Относительность одновременности) вы можете проверить использовал ли
Эйнштейн в своей СТО явление относительности одновременности или только
пофантазировал на эту тему в своих статьях. А на форме 12 (Потенциалы и силы) вы
сможете проверить не только соблюдение ПО наблюдателей объекта при наблюдении за объектом исследования из разных
ИСО, но и посмотреть чему же на самом деле в СТО и ОТО равна скорость
распространения света и гравитации. Или, например, на форме 13 (Удар) вы
сможете проверить действительно ли в СТО сохраняется импульс системы, а на
форме 5 (Ящик) проверить действительно ли в СТО энергия эквивалентна массе или
это только фантазии Эйнштейна и его современных сторонников, и т.д.
В общем программа позволяет экспериментально проверить практически
все основные фантазии Эйнштейна, которые я подробно рассмотрел в своей статье
"О принципах относительности", где использовал и данные полученные с
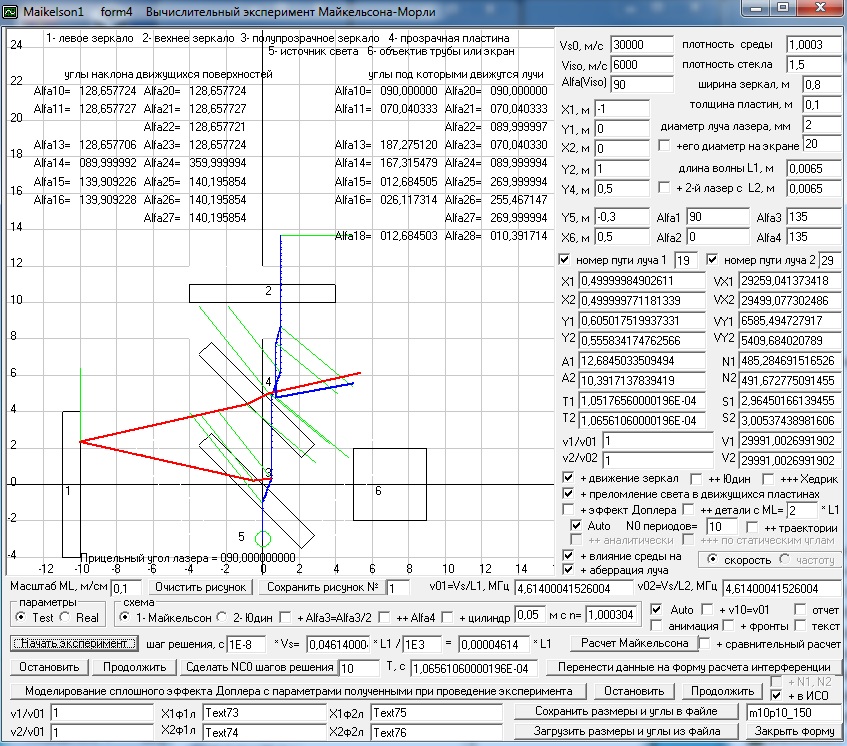
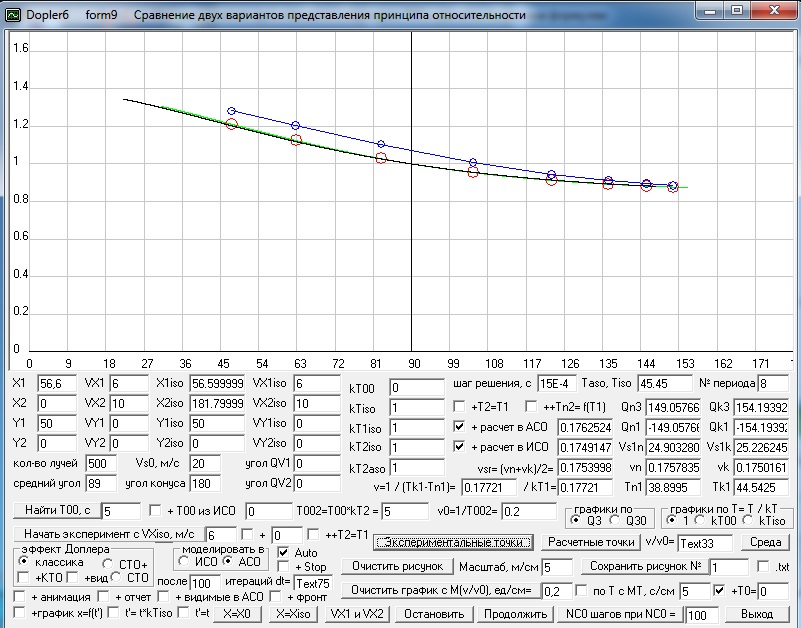
использованием этой программы, а так же программ Dopler6 и Solsys7m5. А ниже вы видите скриншот программы с
загруженной формой 10 (Относительность одновременности), где проверяется
видимая из ИСО движущейся относительно исходной ИСО (у меня это АСО) длина
стержня, который покоится в АСО, в классическом варианте расчета в АСО, т.е.
без использования как преобразований Лоренца, так и преобразований Галилея, т.к.
в рамке <теория> отмечен переключатель <классика в АСО>. Как видим,
расчет без привлечения каких бы то ни было теорий, кроме утверждения о том, что
в АСО скорость света изотропна, что, собственно говоря, и является признаком
АСО, дает совсем не тот результат, что предсказывает СТО, где в данном примере
видимая длина стержня должна была получиться не
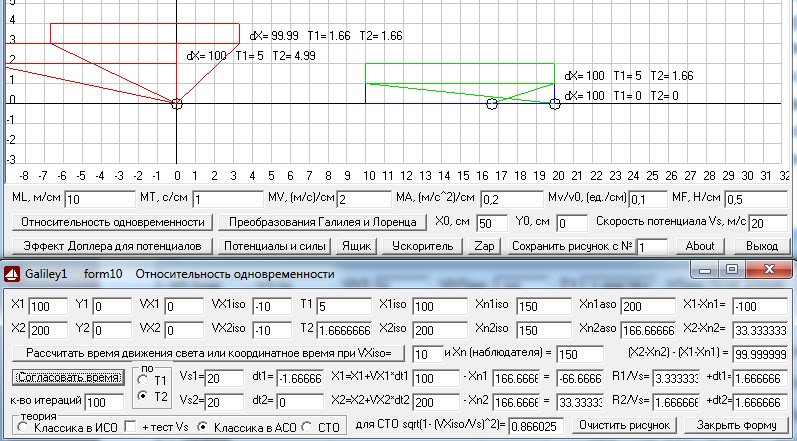
Potencial2 - программа наглядно демонстрирует эффект запаздывания потенциалов по координатам и
различия между потенциалами применяющимися сейчас в физике.
_____Основным назначением программы является наглядная демонстрация эффекта запаздывания потенциалов по координатам, а вторым назначением является демонстрация различий между потенциалами применяющимися сейчас в физике (Ньютона, Кулона, Вебера, Гербера, Лиенара-Вихерта) и предлагаемых мною потенциалов, которые запаздывают по координатам и учитывают динамическое давление поля. При этом я не разделяю потенциалы на создаваемые зарядами и гравитационными массами, хотя, например, потенциалы Гербера никогда не применялись для зарядов, а потенциалы Лиенара-Вихерта в основном используются для зарядов, но, если не учитывать в этой формуле напряженность магнитного поля, то ничто не мешает использовать ее и для гравитационных масс. При этом потенциалы Вебера широко применялись, как для зарядов, так и для гравитационных масс, а то, что потенциалы Кулона ничем не отличаются от потенциалов Ньютона, уже давно всеми признанно. Поэтому можно смело предположить, что идентичные эффекты будут наблюдаться как при взаимодействии зарядов, так и при взаимодействии масс.
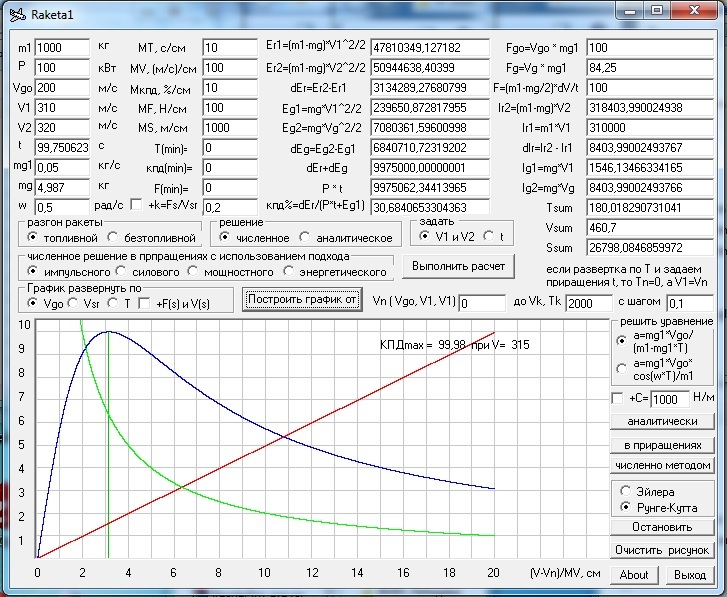
Raketa1 - программа демонстрирует возможности
различных физических подходов (импульсного, силового, мощностного и
энергетического) для математического описания явлений Природы как динамических
систем и возможные методы описания (дифференциальное и интервальное), а также
точность различных методов решения уравнений математического описания.
исполняемый и исходные файлы Raketa1.rar - (Windows 95-98-XP-Vista-7, 0,06 Mb)
_____ В программе сравнивается точность решения задачи
разгона ракеты при математическом описании этого процесса в приращениях и в
дифференциальной форме. При этом описание в дифференциальной форме, полученное
с использованием силового или мощностного подходов для описания явлений
природы, решается потом или аналитически или численными методами Эйлера или
Рунге-Кутта по 4-м коэффициентам, а описание в приращениях, полученное с
использованием импульсного, силового, энергетического или мощностного подходов
для описания явлений природы, так и решается в этих приращениях. Т.к. описание
в приращениях предложено мною впервые, то с его теоретической частью можно
ознакомиться в моей статье «Математическое описание явлений Природы». Там же
можно ознакомиться и с различными подходами, которые в такой классификации
изложены мною тоже впервые, а так же и со всеми формулами, которые используются
в расчетах по этой программе.
Конкретно программа позволяет описать в различных вариантах как разгон
обычной топливной ракеты, так и разгон безтопливной ракеты, которая использует
ионный двигатель для разгона пыли, собираемой ракетой по пути движения. При
этом безтопливная ракета использует для ионизации пыли и для ее разгона в
электрическом поле энергию или солнечных батарей или ядерного реактора, а
количество собираемой ею по дороге в пылесборники пыли в одну секунду равно
количеству пыли, которая потом дозатором подается в двигатель. Таким образом,
начальная масса ракеты для безтопливной ракеты остается неизменной, а у
топливной ракеты каждую секунду уменьшается на величину секундного расхода. При
этом программа позволяет выполнить интервальный расчет разгона этих ракет, как
на одном шаге (полный интервал), когда задаются приращения или времени разгона
или скорости разгона, так и на последовательности приращений (подинтервалов) от
начального значения интервала до конечного значения с заданным шагом.
А во второй части программы мы можем сравнить не только точность
аналитического решения дифференциального описания с решением в приращениях, но
и сравнить их с точностью численных методов решения дифференциального описания.
Здесь рассматривается не только задача разгона топливной ракеты, но и
задача движения массы на которую действует знакопеременная сила, которая
изменяет свое значение по закону cos(w*T), где w это круговая частота. А можно и усложнить эту задачу,
где на массу, кроме знакопеременной силы будет действовать и сила упругости
пружины, к которой будет прикреплена эта масса. При этом решить уравнения
дифференциального описания наших задач мы можем как аналитически, так и
численными методами решения (Эйлера или Рунге-Кутта). А можем использовать и
описание в приращениях и, соответственно, и решать эту задачу методом в
приращениях.
Dopler6 - данная программа позволяет
не только произвести расчеты по нескольким классическим формулам эффекта
Доплера и по всем релятивистским формулам, но и позволяет выполнить различные
вычислительные эксперименты на математических моделях этого эффекта.
исполняемый и исходные файлы
Dopler6.rar - (Windows
95-98-XP-Vista-7, 0,28 Mb)
Данная версия программы отличается от версии Dopler5m только тем, что добавлены две
новые формы 9 и 10 и на форме 3 сделаны мелкие исправления. На форме 9
теперь можно (в отличие от формы 3) моделировать классический и
релятивистский эффекты
Доплера как в АСО при его наблюдение из движущейся относительно нее
ИСО, так и в ИСО, когда и наблюдатель находится внутри этой ИСО, т.е.
движется вместе с ней. Но теперь моделирование можно выполнять только в
среде постоянной оптической плотности, хотя появилось мнго других
возможностей, например, как вы видите на рисунке, графики расчетных и
наблюдаемых данных можно строить непосредственно по ходу выполнения
вычислительного эксперимента (причем по расчетным данным и при расчете
эффекта Доплера в АСО и при одновременном расчете в ИСО).
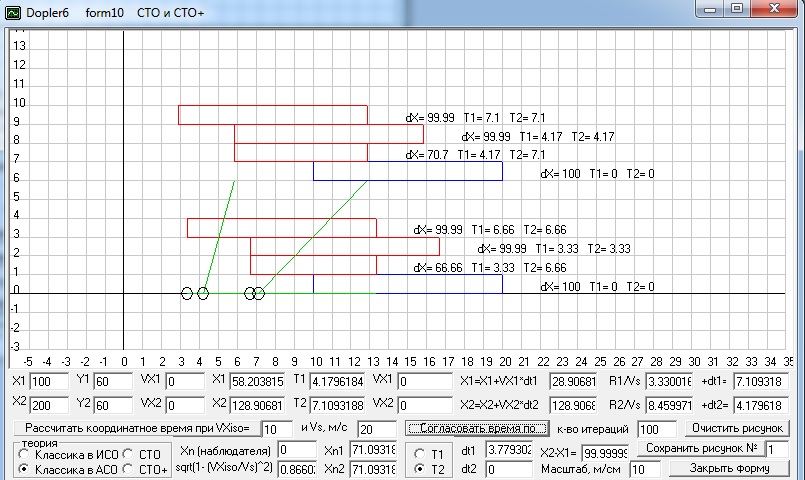
А
на форме 10 можно произвести расчеты видимых, т.е. наблюдаемых в один и
тот же момент времени, координат двух концов стержня, когда он или
покоится в АСО, а наблюдается из движущейся относительно нее ИСО, или
движется относительно АСО, где покоится наблюдатель. Расчет в СТО
согласно преобразований Лоренца действительно дает видимое сокращение
размеров стержня, но только, если стержень покоится в АСО, а
наблюдается из движущейся ИСО, а классический расчет в ИСО, где
используются преобразования Галилея, дает в этом случае наоборот
увеличение видимых размеров стержня. Но, если мы произведем расчет без
каких либо преобразований скоростей стержня и в классике еще и света,
то классический расчет в АСО даст неизменные размеры стержня при его
наблюдение из движущейся ИСО, как это отражено на этом рисунке.
Описание работы с программой смотрите в файле Dopler6_prog.doc.
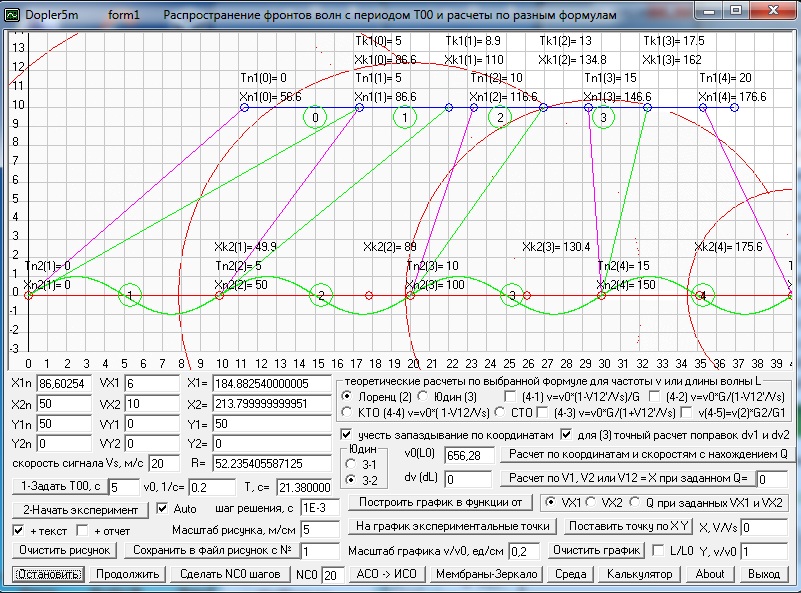
Dopler5m - данная программа позволяет
не только произвести расчеты по нескольким классическим формулам эффекта
Доплера и по всем релятивистским формулам, но и позволяет выполнить различные
вычислительные эксперименты на математических моделях этого эффекта. И на
рисунке первой формы этой программы вы видите один из вычислительных
экспериментов на простейшей математической модели классического эффекта
Доплера, когда у нас от движущегося вдоль оси абсцис источника через заданные
промежутки времени, соответствующие периоду колебаний передатчика,
расположенного на нем, распространяется фронт сферической волны, а при
достижение этим фронтом приемника, который движется на некоторой высоте, у нас
регистрируются моменты прихода сигнала передатчика и по ним вычисляется период
принятого сигнала. А потом программа может по этим данным построить графики и
вывести на них расчетные значения полученные по различным формулам (имитаторам)
эффекта Доплера. А кроме того, программа позволяет сделать и некоторые
вычисления необходимые при обработке данных натурных экспериментов.
исполняемый и исходные файлы
Dopler5m.rar - (Windows
95-98-XP-Vista-7, 0,22 Mb)
Данная версия программы отличается от Dopler5 тем, что я убрал форму с
моделированием эксперимента Майкельсона-Морли, т.к. планирую сделать по нему отдельную
программу, но добавил форму для классического эффекта Доплера, когда
моделируется распространение плоских волн создаваемых источником и принимаемых
приемником, которые имеют мембранную конструкцию. А так же в этой версии на
формах 3 и 6 теперь можно смоделировать и рассчитать классический эффект
Доплера и в эфире не увлекаемом ИСО.
Dopler5 - программа моделирует движение
источника, приемника и волн сигнала передатчика в пространстве между источником
сигнала и приемником, как в математической пустоте, так и в средах переменной
оптической плотности (для света) а также производит расчет и строит графики по
различным формулам для эффекта Доплера и позволяет проанализировать данные,
полученные в различных экспериментах, где наблюдался эффект Доплера.
исполняемый и исходные файлы
Dopler5.rar - (Windows
95-98-XP-Vista-7, 0,24 Mb)
Данная версия программы отличается от Dopler4 тем, что я добавил несколько
форм к проекту, а именно
форма3 - моделирование эффекта Доплера (как классического, так и
релятивистского) для света распространяющегося в средах переменной оптической
плотности.
форма6 - различные варианты расчета по различным релятивистским
формулам при преобразовании координат и скоростей источника и приемника из
одной ИСО в другую ИСО.
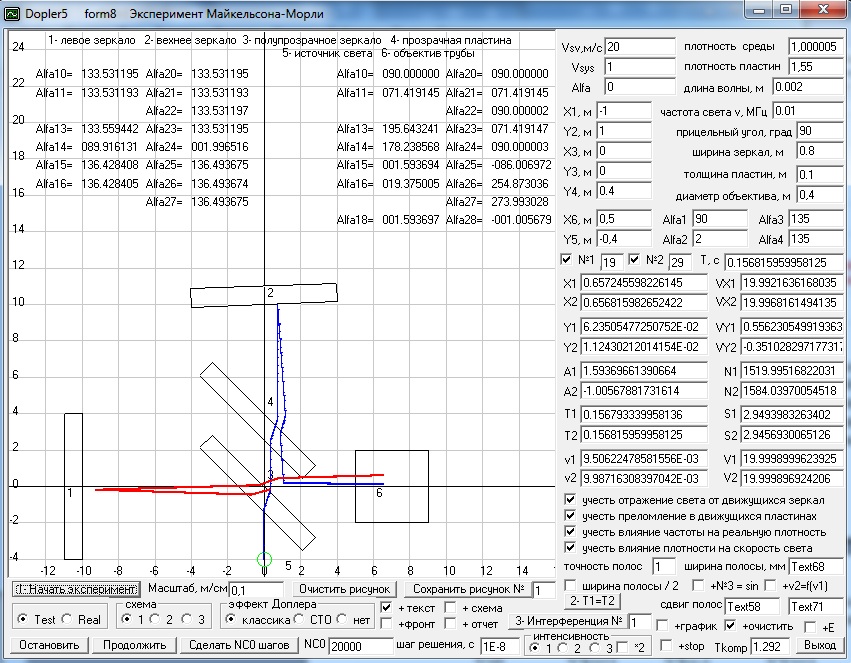
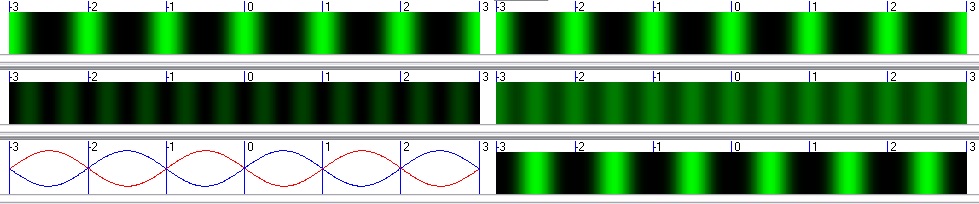
форма8 - моделирование эксперимента Майкельсона-Морли не только с учетом эффекта Доплера, но и с учетом других эффектов влияющих на интерференционную картину. И на нижеприведенных скриншотах Вы видите анимации движения двух лучей в тестовом примере (анимация движения установки по оси абсцисс вправо отключена) и получающихся интерференционных картин при применении различных формул для расчета освещенности экрана.
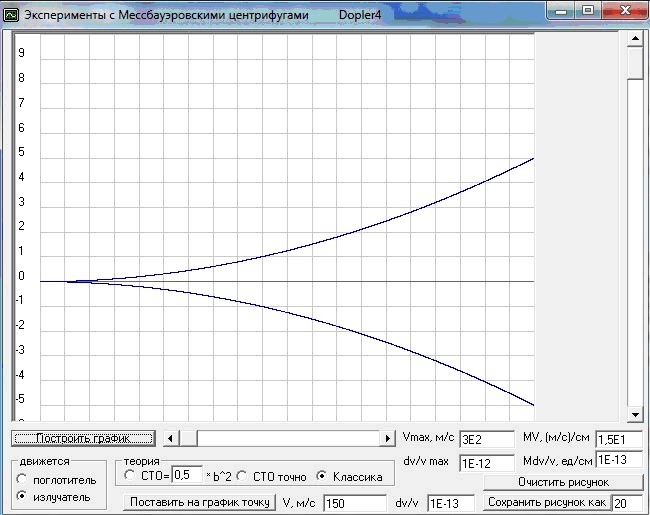
Dopler4 - программа моделирует движение
источника, приемника и волн сигнала передатчика в пространстве между источником
сигнала и приемником, а также производит расчет и строит графики по различным
формулам для эффекта Доплера.
исполняемый и исходные файлы
Dopler4.rar - (Windows
95-98-XP-Vista-7, 0,11 Mb)
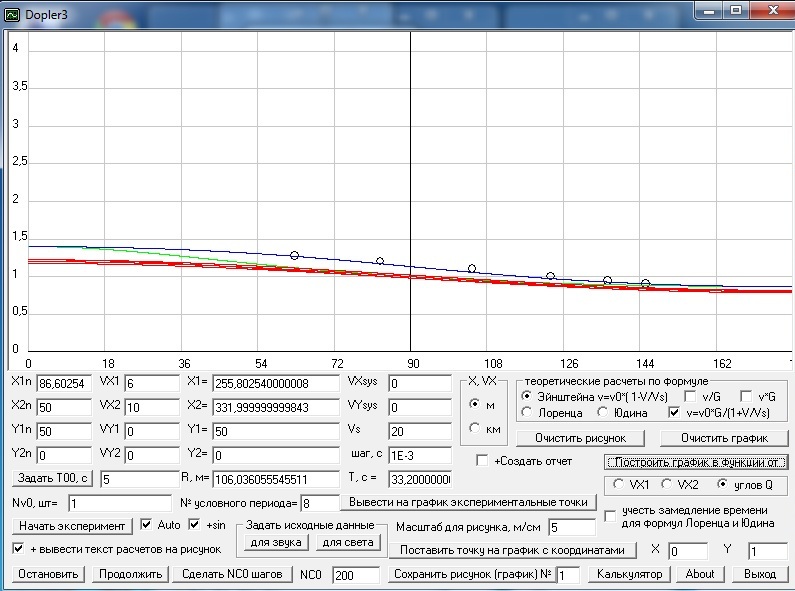
Dopler3 - программа моделирует движение
источника, приемника и волн сигнала передатчика, расположенного на источнике,
как в классическом общем эффекте Доплера, так и в релятивистском, а так же
строит графики по различным формулам для эффекта Доплера.
исполняемый и исходные файлы
Dopler3.rar - (Windows
95-98-XP-Vista-7, 0,08 Mb)
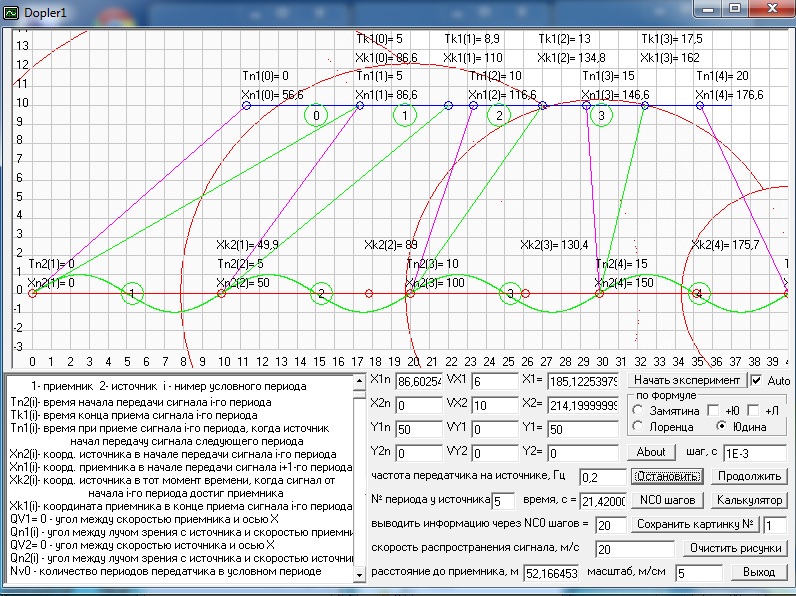
Dopler2 - программа моделирует движение
источника, приемника и волн сигнала передатчика, расположенного на источнике, как
в классическом общем эффекте Доплера, так и в релятивистском, а так же строит графики по различным
формулам для эффекта Доплера.
исполняемый и исходные файлы
Dopler2.rar - (Windows
95-98-XP-Vista-7, 0,06 Mb)
исполняемый и исходные файлы
Dopler1.rar - (Windows
95-98-XP-Vista-7, 0,06 Mb)
Данная программа предназначена не только для наглядной демонстрации
методики расчета по двум формулам общего классического эффекта Доплера, но и
для практических расчетов. В частности на ней можно проиллюстрировать графически
и произвести расчеты эффекта Доплера, как по формуле Лоренца, так и по моей
формуле, которая отличается от формулы Лоренца только использующимися в расчете
углами.
файлы эфемерид DE405 с 1600 по 2020 годы DE405_1.rar - (49,1 Mb)
файлы эфемерид DE405 с 2020 по 2200 годы DE405_2.rar - (22,1 Mb)
А можно производить предварительную
обработка данных оптических наблюдений различных обсерваторий и данных,
полученных по таблицам древних астрономов от Птолемея до Кеплера, для
дальнейшей статистической обработки полученных при этом данных, с целью
получения кинематической теории планет, или производить обработку данных
полученных при моделировании, и в конечном итоге производить окончательную их
обработку с использованием планов многофакторного планирования для
экспериментального определения скорости распространения гравитации и абсолютной
скорости Солнечной системы и многое, многое другое.
Например, программа позволяет по
различным теориям планет (в том числе и по таблицам древних астрономов)
рассчитывать Солнечные и Лунные затмения и транзиты Меркурия и Венеры,
преобразовывать координаты объектов из одной системы координат в другую или на
демонстрационных формах программы уяснить такие вопросы, как расчет аберрации
или запаздывания потенциала по координатам и т.д. и т.п.
При этом, комплекс программ Solsys7m4 является усовершенствованным
комплексом программ Solsys7mmm и в нем выполняются все
операции, которые выполнялись и в программах Solsys7, Solsys7m и Solsys7mm, а полное описание всех возможностей
программы и правил работы с ней читайте в файле Solsys7m4.doc, который я
распространяю вместе с программой в файле архива Solsys7m4.rar. В этот же архив я поместил и
файл New_JPL_Ser, где привожу данные по своей теории планет -Ser и
теориям планет Ньюкома -New и лаборатории реактивного движения
-JPL. Там же находится и описание файлов в папке Plan00, которые я использовал
при написание 3-ей редакции статьи "Влияние скорости гравитации на
смещения параметров орбит планет".
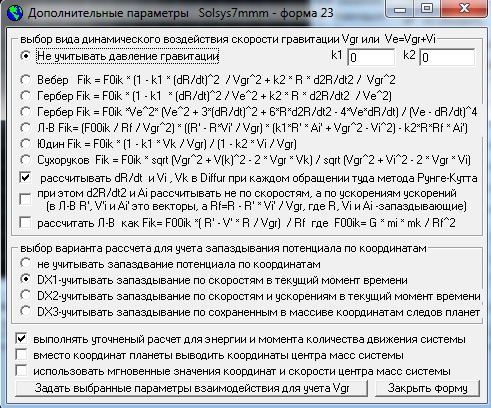
А по сравнению с программой Solsys7mmm я убрал возможность задавать на форме 1 данные
по двойным пульсарам с формы 25, т.к. теперь это можно легко сделать и на самой
форме 1, и добавил возможность работать на формах 1, 2, 20 и 25 с углами
наклона орбит более 10 градусов, что для планет Солнечной системы было не
критично, а для произвольных систем, например, для двойных пульсаров очень
чувствительно. Так же на формах 1, 20 и 25 немного уточнен расчет по различным
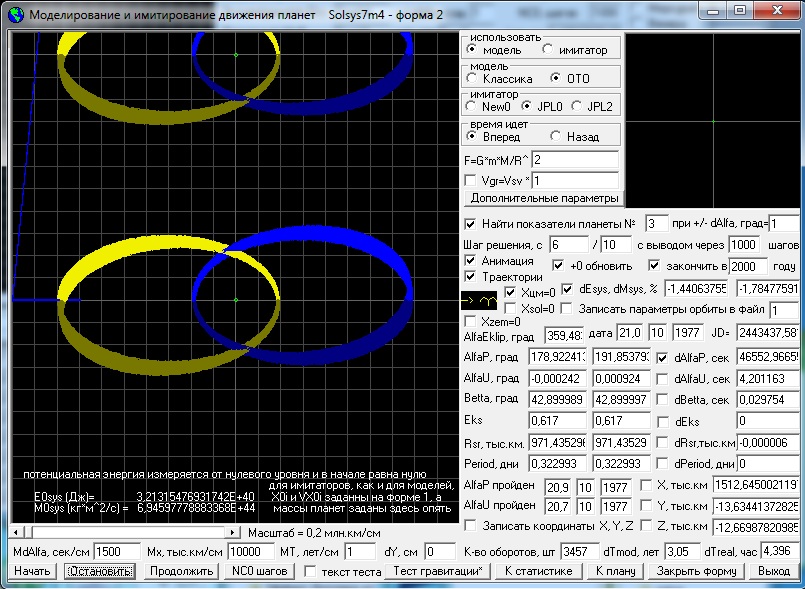
параметрам орбит начальных данных для моделирования. А на нижеприведенном
скриншоте формы 2, Вы видите моделирование движения двойного пульсара PSR B1913+16 с использованием ОТО Эйнштейна, где мы явно видим поворот
эллипсов пульсара и его компаньона в плоскости их орбит на 4,24 град за год,
что, собственно говоря, и должно было быть согласно ОТО.
P.S. Если вы скачали файлы исходного кода программы, то для работы с ними в оболочке языка программирования VisualBasic 6.0, на котором и написана эта программа, разархивируйте их из архива Solsys7m4_bas.rar в папку Solsys7m4, т.е. туда же, куда вы разархивировали и исполнительный файл Solsys7m4.exe вместе с папками данных. Но, если у вас нет этой оболочки, то можете посмотреть код и любой программой для просмотра текста, например, Блокнотом. Только в последнем случае у вас в начале будет показана дополнительная информация относящаяся к визуальному отражению форм программы (примерно половина всего текста), а сам код программы начнется со строчки Private Sub Form_Load().
исполняемый
файл программы и прочие файлы Solsys7m_exe.rar - (Windows
95-98-XP-Vista-7, 14,3 Mb)
файлы эфемерид DE405 с 1600 по 2020 годы DE405_1.rar - (49,1 Mb)
файлы эфемерид DE405 с 2020 по 2200 годы DE405_2.rar - (22,1 Mb)
файлы вычислительных экспериментов Plan0.rar - (18,7 Mb)______Отдельные подпрограммы комплекса Solsys7m позволяют
моделировать движения объектов в Солнечной системе по трем координатам с учетом
скорости распространения гравитации и имитировать это движения планет по
различным теориям движения планет, производить предварительную обработка данных
оптических наблюдений различных обсерваторий и данных полученных по таблицам
древних астрономов от Птолемея до Кеплера для дальнейшей статистической
обработки полученных при этом данных, а так же данных полученных при
моделировании, и в конечном итоге производить окончательную их обработку
с использованием планов многофакторного планирования для экспериментального определения скорости
распространения гравитации и абсолютной скорости Солнечной системы.
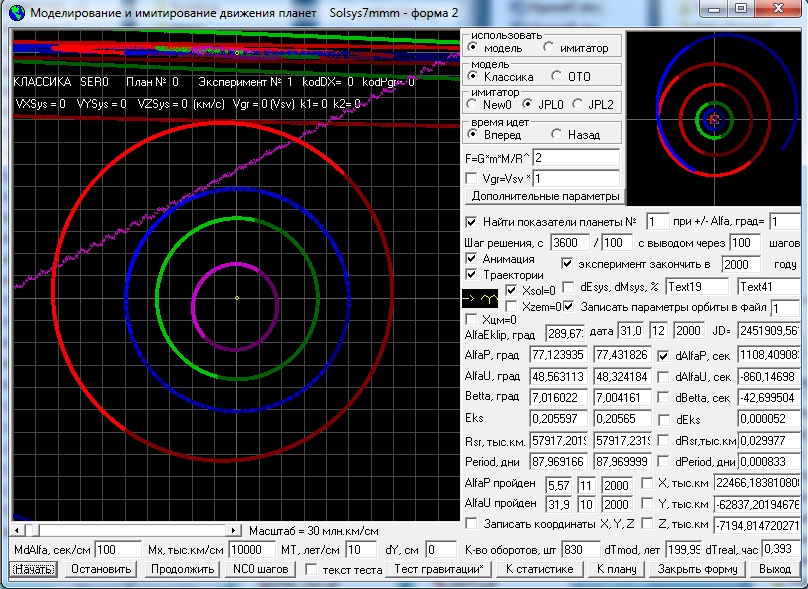
Программа Solsys7m включает в себя и многие другие подпрограммы, которые так или иначе связаны с ее основным назначением. Например, позволяет по различным теориям планет (в том числе и по таблицам древних астрономов) рассчитывать Солнечные и Лунные затмения и транзиты Меркурия и Венеры, преобразовывать координаты объектов из одной системы координат в другую и на демонстрационных формах программы позволяет лучше уяснить такие вопросы, как расчет аберрации или запаздывания потенциалов по координатам и многое другое. Версия программы Solsys7m является улучшенным вариантом программы Solsys7, в которой исправлены две ошибки (расчет запаздывания по координатам на форме 2 и оптимизация параметров на формах, где используется многофакторное планирование) и добавлена возможность учитывать при моделировании динамическое давление, а также внесены другие мелкие изменения. Возможные варианты расчета динамического давления и запаздывания по координатам я привожу на скриншоте программы.

Solsys7 - моделирование движения объектов в Солнечной системе по трем координатам с учетом скорости распространения гравитации и имитирование движения планет по различным теориям движения планет и статистическая обработка полученных при этом данных, а также статистическая обработка данных оптических наблюдений различных обсерваторий и данных полученных по таблицам древних астрономов от Птолемея до Кеплера и использование планов многофакторного планирования для экспериментального определения скорости распространения гравитации и многое другое.
Внимание. В программе Solsys7 на форме 2 не правильно расчитывается запаздывание по координатам (на форме 7 правильно) поэтому я выложил и отдельно исполняемый файл Solsys7error.exe, где эта ошибка исправлена, и если будете моделировать движение объектов на форме 2 с учетом запаздывания, т.е. когда отмечен чекбокс <Vgr=Vsv*>, то используйте этот файл, а для всех остальных расчетов лучше использовать программы Solsys7.exe, т.к. я не уверен, что исправиленный вариант (релиз 2.00.630) полностью соответствует по содержанию (если не считать косметических исправлений) последнему релизу программы (2.00.632), который я выложил ранее. А сейчас я уже заканчиваю модернизированный вариант программы Solsys7m (релиз 2.00.746).
исполняемый файл с исправлением на форме2 Solsys7error.zip - (Windows 95-98-XP-Vista-7 418 kb)
исполняемый файл и прочие (без файлов данных) Solsys7minus.zip - (Windows 95-98-XP-Vista-7 1,7 Mb)
полная версия программы Solsys7exe.rar - (Windows 95-98-XP-Vista-7 14,3 Mb)
копия Solsys7exe.rar на файлохранилище Яндекса - (Windows 95-98-XP-Vista-7 14,3 Mb)
копия Solsys7exe.rar на Яндек диске - (Windows 95-98-XP-Vista-7 14,3 Mb)
_____Хотя данная программа и является усовершенствованной версией программы Solsys6, но наличие в ней многих дополнительных форм, и улучшенное представление уже существующих форм делает ее законченным программным комплексом по теориям планет, т.е. как для изучения существующих теорий планет, так и для создания новых. А т.к. описать все возможности этой версии программы в коротком анонсе не представляется никакой возможности, то я их изложил в файле Solsys7.doc, который распространяю вместе с программой в файле архива Solsys7exe.rar. В этот же архив я поместил и файл NewJPLSer, где привожу данные по своей теории планет -Ser (от Меркурия до Марса) и теории планет Ньюкома -New и НАСА, а конкретно лаборатории реактивного движения -JPL.
Solsys6 - моделирование движения объектов в Солнечной системе по трем координатам с учетом скорости распространения гравитации и имитирование движения планет по различным теориям движения планет и статистическая обработка полученных при этом данных, а также статистическая обработка данных оптических наблюдений различных обсерваторий и данных полученных по таблицам древних астрономов от Птолемея до Кеплера и использование планов многофакторного планирования для экспериментального определения скорости распространения гравитации и многое другое.
исполняемый файл и прочие файлы Solsys6exe.rar - (Windows 95-98-XP-Vista-7, 2,75 Mb)
два первых файла из эфемерид DE200 и DE405 JPL.rar - (4,45 Mb)
24 файла с данными 4-го плана для Меркурия Plan4.rar - (1,0 Mb)
_____Хотя данная
программа и является
усовершенствованной версией
программы Solsys5, но наличие в ней 10-ой
формы обработки первичных
наблюдательных данных позволяет
говорить о ней теперь как о
законченном научно-вычислительном
комплексе, как для обработки данных
наблюдений, так и для получения
данных на различных моделях и
имитаторах и их обработки. А, если
учесть и то, что теперь в программе
есть и такие дополнительные формы,
как сравнение движения планет по
эксцентру Птолемея и по эллипсу,
преобразование координат из одной
системы в другую, наглядное
объяснение принципов определения
планетной и звездной аберрации и т.д.,
то теперь я даже затрудняюсь
сказать, какие задачи на этой
программе нельзя решить. И, т.к.
описать все возможности этой
версии программы в коротком анонсе
не представляется никакой
возможности, то я их изложил в файле
Solsys6.doc, который я распространяю
вместе с программой в файле архива
Solsys6exe.rar. В этот же архив я поместил
и таблицу 11d со значениями вековых
смещений параметров орбит,
полученных мною на различных
имитаторах Солнечной системы и на 2-х
классических моделях с разным
показателем степени у радиуса в
формуле притяжения Ньютона, а также
файл Solsys6info.doc, где я даю чисто
технические пояснения по установке
программы и по особенностям ее
работы под разными версиями Windows.
Отличием 6-ой версии программы от 5-ой
является и то, что я разделил на две
формы статистическую обработку
данных и обработку данных плана
многофакторного планирования для
определения скорости гравитации.
Но основное отличие, конечно же, в
наличие 10-ой формы, т.е. формы, где
обрабатываются данные наблюдений.
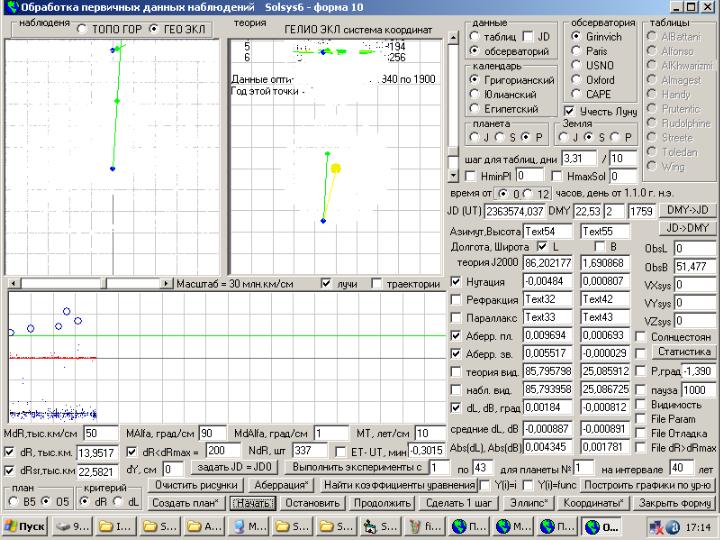
По этому, ниже я привожу скриншот
этой формы, где обрабатываются
наблюдательные данные Гринвичской
обсерватории за Меркурием с 1940 по
1900 год. А пока на этой форме можно
обработать данные наблюдений за
планетами 5-и обсерваторий
Гринвичской, Парижской,
Оксфордской, USNO и CAPE примерно с 1800
года по 1950 год. И файлы с данными
оптических наблюдений этих
обсерваторий, которые я скачал с
сайта Парижского Бюро долгот http://www.bdl.fr/host/podb/podb2/int_merc_tr.html , я распространяю
вместе с программой. На этой же
форме можно обработать и данные
наблюдений древних астрономов,
которые они оформили в виде таблиц
для расчета координат планет и
Солнца на заданную произвольную
дату. Конкретно Вы можете работать
со следующими таблицами – Птолемея,
Индийскими, Аль Хорезми, Аль
Баттани, Толедскими, Альфонсовыми,
Прусскими, Кеплера, Стрита и Винга,
которые я скачал сайта Robert Harry van Gent http://www.phys.uu.nl/~vgent/astro/ancientephemerides.htm и которые я также
распространяю вместе с самой
программой.
P.S. Т.к. каждый файл эфемерид DE405 для имитатора JPL2, где аппроксимируется движение планет и Солнца на промежутке в 20 лет, занимает в распакованном виде около 5 Mb, то разместить их все с 1600 по 2020 год на своих домашних страницах я не могу. По этому, я только первый файл из этих эфемерид с 1600 по 1620 годы, т.е. файл ascp1600.405 разместил в архиве JPL.rar , чтобы Вы просто попробовали, что имитатор работает (этот архив я создавал для 5-ой версии программы, где используются и эфемериды DE200, по этому в архиве находится и файл ascp1600.200). Но, если Вы не собираетесь сами работать с этими эфемеридами, то можете просто обработать на 6-ой форме файлы, полученные с помощью этих эфемерид, которые находятся в папке JPL и которые я распространяю вместе с программой. А, если Вы собираетесь сами поработать с этими эфемеридами, то скачайте их самостоятельно с сайта JPL отсюда ftp://ssd.jpl.nasa.gov/pub/eph/export/ . А вот для того, чтобы Вы поняли, что Вам надо получить при проведение экспериментов по плану многофакторного планирования для оптимизации скорости распространения гравитации на 15-ой форме, я уже полученные мною на 5-ой версии программы 24 файла с первичными данными по Меркурию с уровнями варьирования факторов по 4-му плану и обработанные данные этих 24 экспериментов поместил в архив Plan4.rar .
Solsys5.0 - моделирование движения объектов в Солнечной системе по трем координатам с учетом скорости распространения гравитации и статистическая обработка полученных данных с возможностью их обработки по плану многофакторного планирования для 4-х факторов.
исполняемый файл и прочие файлы Solsys5exe.rar - (Windows 95-98-XP-Vista-7, 549 kb)
два первых файла из эфемерид DE200 и DE405 JPL.rar - (4,45 Mb)
24
файла с данными 4-го плана для
Меркурия Plan4.rar - (1,0 Mb)
_____Хотя данная
программа и является
усовершенствованной версией
программы Solsys4, но наличие в ней на 3-ей
форме мощного блока статистической
обработки данных позволяет
говорить о ней как о принципиально
другой программе и при этом
профессиональной теперь во всех
отношениях. Правда и первые две
формы, где задается состав объектов
моделируемой системы и
определяются параметры орбит
известных объектов (планет) а затем
на классической математической
модели системы проводятся
вычислительные эксперименты, тоже
подверглись существенным
изменениям. Во-первых, я выкинул из
них многие функции, которые нужны
для очень специфических условий, т.к.
размер программы стал просто
зашкаливать за все разумные
пределы. А во-вторых, я не только
сделал их более удобными и уточнил
значения параметров орбит планет и
астрономические постоянные, но и
добавил определение смещения еще
для одного параметра (большая
полуось эллипса) к уже имевшимся
параметрам орбит (перигелий
планеты, узел восхождения, наклон
орбиты и эксцентриситет) и для
одного показателя (период
обращения планет). А вот, в третьих,
я все таки согласился использовать
в качестве данных наблюдений
эфемериды DE200 и DE405, которые созданы
в Лаборатории реактивного движения
(JPL, США) и кругом рекламируются как
данные наблюдений. А согласился по
одной простой причине. Других
обработанных, т.е. приведенных к
какой то системе координат, данных
наблюдений за планетами на больших
промежутках времени 200…400 лет на
сегодняшний день, быстрее всего,
просто не существует, т.к., даже в
нашей космической державе, сейчас
Астрономический ежегодник и
Морской астрономический альманах
выходят с данными, полученными из
этих эфемерид. Таким образом,
теперь на 2-ой форме можно проводить
вычислительные эксперименты не
только на математической модели
системы, но и на ее имитаторе, т.е.
определять координаты планет с
помощью аппроксимаций, которые
представлены в этих эфемеридах в
виде полиномов Чебышева.
Не маловажным является и то, что
теперь я к вспомогательной форме,
которая наглядно показывала все
параметры орбит, определяемые в
программе, добавил еще три
вспомогательные формы. И если в 4-ой
версии скорость системы по осям
координат просто задавалась на 1-ой
форме, то теперь, перейдя на
дополнительную форму скоростей
Солнечной системы, Вы можете не
просто задать эту скорость, но и
наглядно посмотреть, как в
численном виде, так и в графическом
все возможные варианты суммарной
скорости системы при сложение или
вычитание всех составляющих
скорости Солнечной системы,
известных мне из литературных
источников. Например, это скорость
системы относительно центра
галактики или скорость центра
галактики относительно
реликтового излучения и т.д. Очень
полезной является и форма
демонстрирующая (опять в численном
и графическом виде) различие между
силами притяжения между планетами
при различной скорости
распространения гравитации. А в
связи с тем, что файловая система
самой программы из-за возможности
проводить эксперименты по планам
многофакторного планирования
стала достаточно сложной, я сделал
еще одну вспомогательную форму, где
наглядно представлена файловая
система 5-ой версии программы.
Причем, я заранее предусмотрел
изменения, которые я планирую
внести в 6-ю версию программы, и по
этому все файлы с данными,
полученные Вами в 5-ой версии можно
будет использовать и в 6-ой.
К сожалению, описать все
возможности этой версии программы
в коротком анонсе не
представляется никакой
возможности. Мне даже описание
программы в форме About пришлось
сократить страниц на 6, т.к. больше 21-ой
страницы в текстбоксе формы не
умещается. А, т.к. читать 21-у
страницу в маленьком справочном
окошке не очень удобно, я даже
создал специальный текстовый файл
About.doc и поместил его вместе с
другими файлами, необходимыми для
работы программы в архив Solsys5exe.rar.
По этому, чтобы узнать все
возможности программы и как их
реализовать, лучше распечатайте
файл About.doc и внимательно его
почитайте. Хотя управление
программой интуитивно понятно и
без описания, но в ней столько
всяких тонкостей, что разобраться в
них без описания не возможно, а
особенно если Вы не сильны в
статистической обработке данных
или вообще ничего не слышали о
многофакторном планировании. И
даже, если Вы хорошо изучили работу
4-ой версии программы, то форма
статистической обработки данных
является для нее принципиально
новой и описание надо обязательно
читать.
А что касается возможности этой
версии программы, то я скажу только,
что созданная мною методика
обработки данных параметров планет,
замеренных на 2-ой форме программы,
как при проведение вычислительных
экспериментов на математических
моделях, так и на математических
имитаторах, позволяет получить
данные по вековым смещениям
параметров орбит планет как
минимум на порядок надежнее и
точнее, чем в 4-ой версии. А
возможность проводить
эксперименты не вслепую, а по плану
многофакторного планирования,
позволяет экспериментально
определить скорость
распространения гравитации и
абсолютные скорости движения
Солнечной системы по трем
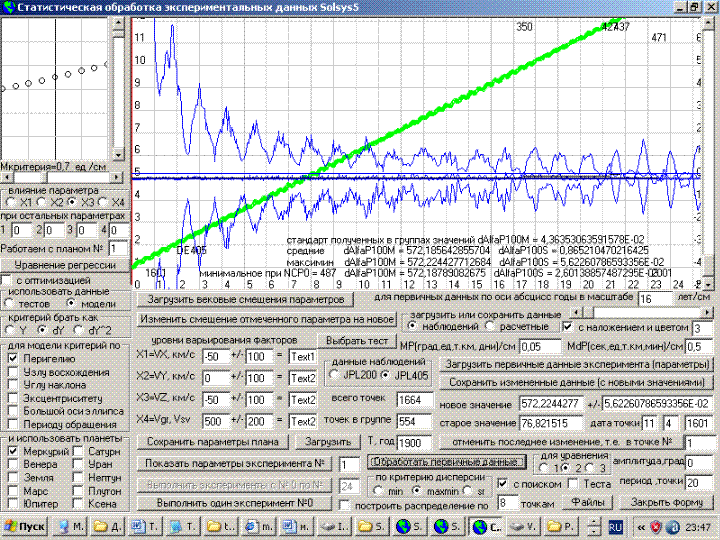
координатным осям. Скриншот 3-ей
формы программы, где показан момент
определения по первичным данным,
полученным на имитаторе DE405
наблюдаемого значения смещения
перигелия Меркурия по критерию
максимина при линейной
аппроксимации первичных данных,
показан ниже.
P.S. Т.к. каждый
файл эфемерид DE200 и DE405, где
аппроксимируется движение планет и
Солнца на промежутке в 20 лет,
занимает в распакованном виде
около 5 Mb, то разместить их все с 1600
по 2000 год на своих домашних
страницах я не могу. По этому, я
только первые файлы из этих
эфемерид с 1600 по 1620 годы, т.е. файлы
ascp1600.200 и ascp1600.405 разместил на одной
из своих страниц http://modsys.narod.ru в
архиве JPL.rar , чтобы Вы просто
попробовали, что имитаторы
работают, а, полученные с их помощью
данные по всем планетам, которые
нужны для их статистической
обработки на 3-ей форме, я поместил в
папках JPL/200 и JPL/405 вместе с
программой и Вы можете работать уже
с ними. Если Вы собираетесь сами
работать с этими эфемеридами, то
скачайте их самостоятельно с сайта
JPL отсюда ftp://ssd.jpl.nasa.gov/pub/eph/export/ . А, т.к.
сейчас даже Астрономические
ежегодники перешли с эфемерид DE200
на более новые эфемериды DE405, то
эфемериды DE200 можете и не скачивать.
Тем более, что обработка мною
полученных данных как по
эфемеридам DE200, так и по эфемеридам
DE405, показала, что они практически
идентичны. А для того, чтобы Вы
поняли, что Вам надо получить при
проведение экспериментов по плану
многофакторного планирования, я
уже полученные мною 24 файла с
первичными данными по Меркурию с
уровнями варьирования факторов по 4-му
плану поместил в архив Plan4.rar . И,
если Вы скачаете эту папку с
файлами и поместите ее рядом с уже
существующими 3-я папками планов,
которые распространяются вместе с
самой программой, то можете
получить уравнение регрессии для
выбранного Вами критерия
оптимизации. Поэкспериментируйте с
уже существующими файлами данных и
Вы быстрее поймете что откуда
берется, куда передается и зачем.
Solsys4.0 - моделирование движения объектов в Солнечной системе по трем координатам с учетом скорости распространения гравитации.
исполняемый файл Solsys4exe.zip - (Windows 95-98-XP-Vista-7, 114kb)
_____Данная
программа является
усовершенствованной версией
программы Solsys3 и теперь движение
планет моделируется по 3-м
координатам и есть возможность
изменить состав планет входящих в
систему, а также теперь можно
определять не только смещение
перигелия планеты, но и его узла
восхождения, угла наклона орбиты и
эксцентриситета. А, проделанная
работа по статистической обработке
данных, позволила значительно
уменьшить дисперсию замеряемых
показателей. При этом перечень
показателей работы системы,
которые теперь можно
экспериментально определить
настолько расширился, что я даже
затрудняюсь сказать какой
показатель функционирования
системы теперь нельзя определить и
какие исходные данные нельзя
задать (посмотрите лучше описание
программы и два скриншота
программы с формы данных и формы
самого эксперимента).
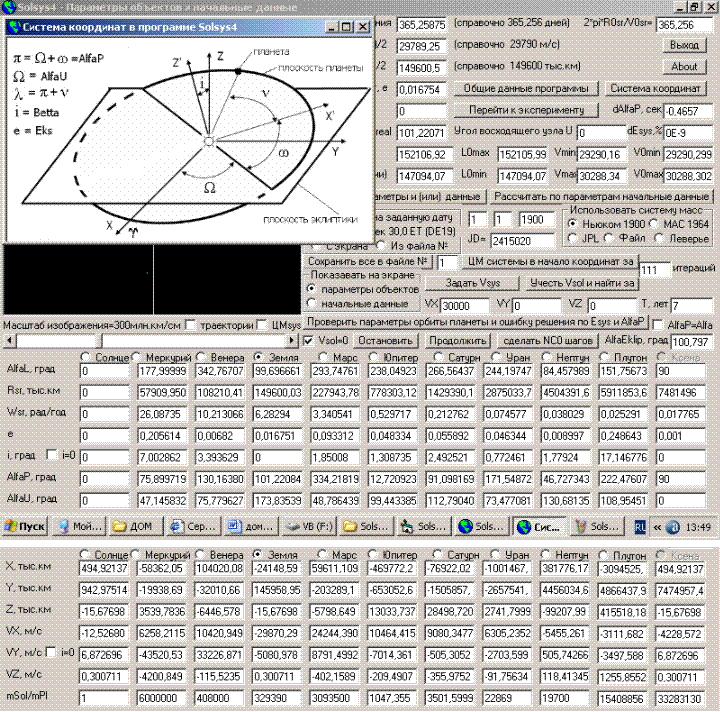
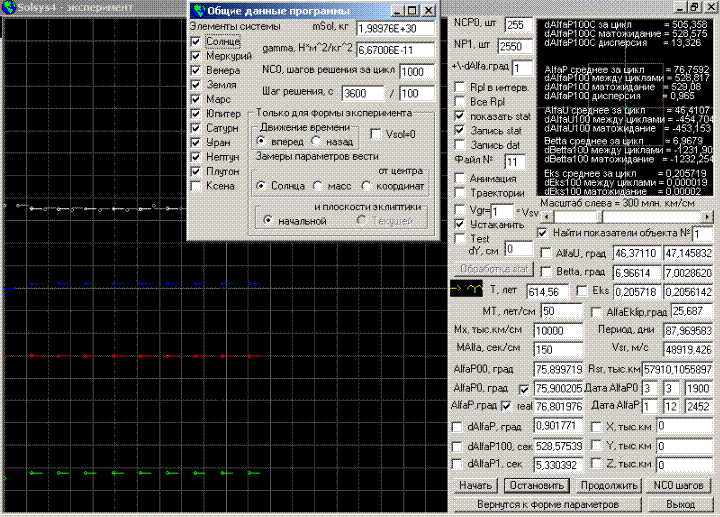
Очень
существенным является и то, что
теперь в программе можно задать
скорость распространения
гравитации. В результате сила
притяжения между планетами теперь
вычисляется по той же формуле
Ньютона, но исходя не из текущего
положения двух взаимодействующих
тел, а с учетом времени на
распространение гравитации, когда
одну планету рассматриваем в том
положение, где она находится сейчас,
а положение второй, которая
действует на первую, определяем в
том положение, где она находилась
несколько минут назад, необходимых,
чтобы гравитация от нее достигла
первой планеты. Результаты
полученные при разных значениях
скорости движения всей Солнечной
системы показывают не только то,
что необходимый результат по
смещению перигелия Меркурия (575
угловых секунд) в этом случае может
быть получен и без измышления
гипотез, т.е. без теории
относительности Эйнштейна, но и то,
что в системе движущейся
прямолинейно и равномерно события
происходят совсем не так как в
покоящейся системе, и такую систему
нельзя считать инерциальной.
Однако для того, чтобы получить
нужный результат по смещению
перигелия для Меркурия (575 угловых
секунд) и нужные значения для
других планет (не измышляя новых
гипотез), необходимо точно знать
скорость движения Солнечной
системы и скорость распространения
гравитации. Ни то ни другое нам не
известно (хотя по скорости
Солнечной системы имеется
множество разнообразных данных) и
по этому надо проводить поисковые
эксперименты, но этим я займусь уже
в 5-ой версии программы. При этом
обращаю особое внимание на то, что
учет скорости распространения
гравитации пока осуществляется по
очень примитивному алгоритму и по
этому он удовлетворительно
работает только в покоящейся
системе, а следовательно и
результаты, полученные в
движущейся системе, следует
считать предварительными и
требующими обязательного
уточнения. При этом, учитывая, что 4-я
версия получилась настолько
сложной, что я сам иногда путаюсь в
коде программы (даже при наличие
своих же комментариев), код
программы уже не может быть
использован в учебных целях и я его
не выкладываю.
Solsys3.0 - моделирование движения объектов в Солнечной системе.
исполняемый файл Solsys3exe.zip - (Windows 95-98-XP-Vista-7, 42 kb)
исходные файлы Solsys3vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 24 kb)
_____Данная программа является усовершенствованной версией программы Solsys2. Переработке подвергся не только дизайн, но и на порядок увеличено быстродействие кода программы. Однако, основным ее отличием от 2-ой версии является наличие возможности экспериментально определить различные показатели функционирования Солнечной системы, например, такие как период обращения различных планет и параметры полученных орбит, если считать их эллиптическими, такие как эксцентриситет, расстояния до Солнца в афелии и перигелии и скорости в этих точках. Кроме этого в программе выводятся также значения этих показателей приведенные в справочной литературе, а для некоторых и полученные расчетным путем. Более подробно об этом можно почитать в описание программы и посмотреть в комментариях к коду программы.
_______Но основным
побудительным мотивом, заставившим
меня модернизировать программу,
явилось желание определить
экспериментально смещение
перигелия Меркурия. Из
литературных источников известно,
что все орбиты планет со временем
эволюционируют, т.е. их эллипсы как
бы поворачиваются, но наиболее
заметен этот эффект только для
Меркурия. Наблюдения показывают,
что за 100 лет его перигелий
поворачивается на 5600" (угловых
секунд), где 5025" это поворот самой
системы отсчета, а 575" это
динамическое смещение,
обусловленное влиянием объектов
Солнечной системы. Как пишут в
литературных источниках, 532"
объясняются влиянием объектов
Солнечной системы классической
механикой, а 43" объясняются
релятивистской механикой. Моя
модель, где все планеты движутся в
одной плоскости, дает значение 544"…549"
(интервал это не погрешность
решения). С учетом заметного угла
наклона орбиты Меркурия (7 градусов)
будет немного меньше, но никак не 532",
хотя и полученный результат можно
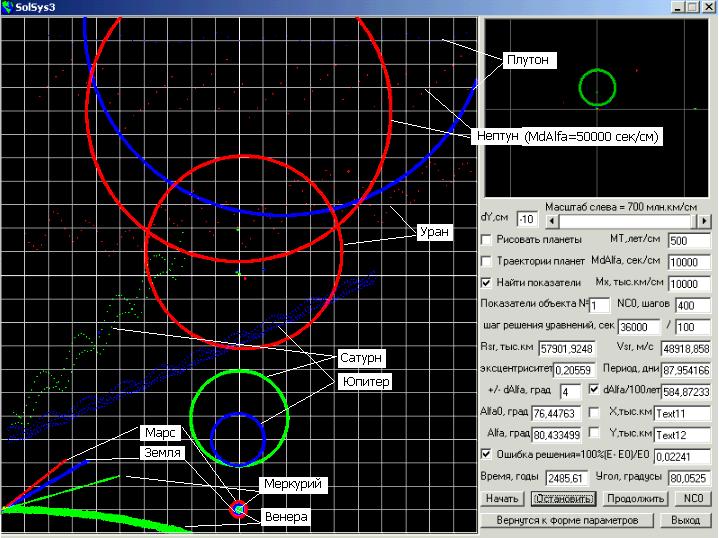
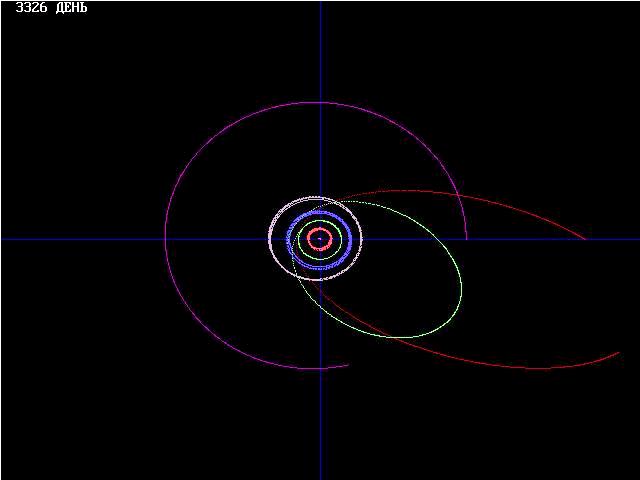
считать вполне удовлетворительным. Графики
зависимости абсолютного смещения
перигелиев планет (не за 100 лет) в функции
времени приведены на скриншоте
второй формы программы, где масштаб
для времени (по оси абсцисс) 500 лет/см и смещение угла перигелия для всех
планет 10000 сек/см, а для Нептуна 50000,
т.к. у него очень сильные колебания
угла, как в одну, так и в другую
сторону от некоторого среднего
значения. При этом у Венеры смещение
перигелия происходит в
противоположную сторону.
Solsys2.0 - моделирование движения объектов в Солнечной системе.
исполняемый файл Solsys2exe.zip - (Windows 95-98-XP-Vista-7, 774 kb)
исходные файлы Solsys2vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 46 kb)
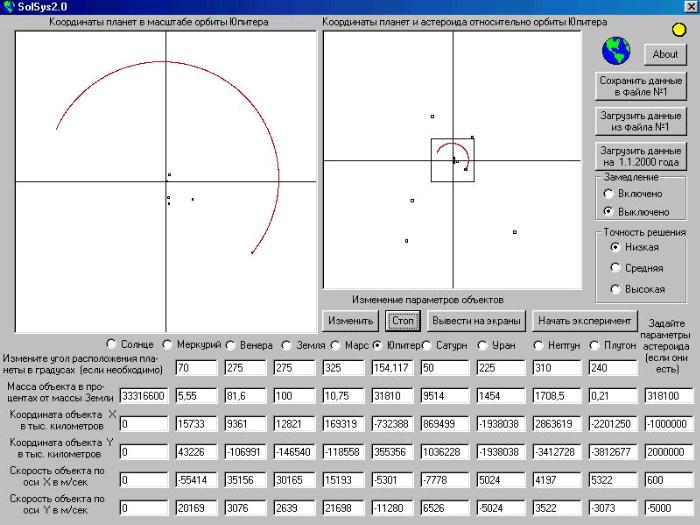
_____Программа моделирует движение Солнца, девяти планет и произвольного объекта, например, астероида, который приближается к Солнечной системе. И хотя программа интересна сама по себе с познавательной точки зрения, но особую привлекательность ей придает возможность смоделировать последствия от встречи с астероидом. И если он будет достаточно бодьшой, то даже, если он пролетит далеко от Земли это может иметь катострофические последствия для Земли, например, она может в таком случае столкнуться с Венерой или вообще улететь за пределы Солнечной системы да и само Солнце может потихоньку полететь куда нибудь. Многим это кажется невероятным, но давайте не будем рассуждать, а обратимся к формулам, которые моделируют движение объектов в Солнечной системе используя только законы Ньютона. Правда все орбиты обектов рассматриваются в этой версии в одной плоскости, хотя они на 1-3 градуса отклонены от плоскости орбиты Земли, а Меркурия и Плутона еще больше, но трехмерная модель потребует от ЭВМ такого быстродействия, что не любой персональный компьютер справится, а уменьшение точности решение меньше чем “низкое”, которое можно изменить в программе, приводит к тому, что дифференциальные уравнения идут в “разнос” и Меркурий с его параметрами не выдерживает этого и улетает.
_____При загрузке программы вы видите параметры объектов, которые загружаются по умолчанию. Их можно вывести на графические экраны, нажав кнопку “вывести на экраны”, а выбрав конкретный объект, можно установить для него произвольные параметры. Все параметры (кроме масс объектов) можно в любой момент сохранить в файле, а позднее наоборот загрузить эти параметры из файла. Кроме того можно загрузить параметры объектов по состоянию на 1.1.2000 г., нажав соответствующую кнопку. После того как все параметры заданы можно начинать эксперимент, для чего необходимо нажать соответствующую кнопку и загрузить вторую форму, которя также имеет два графических экрана и элементы управления ходом эксперимента.
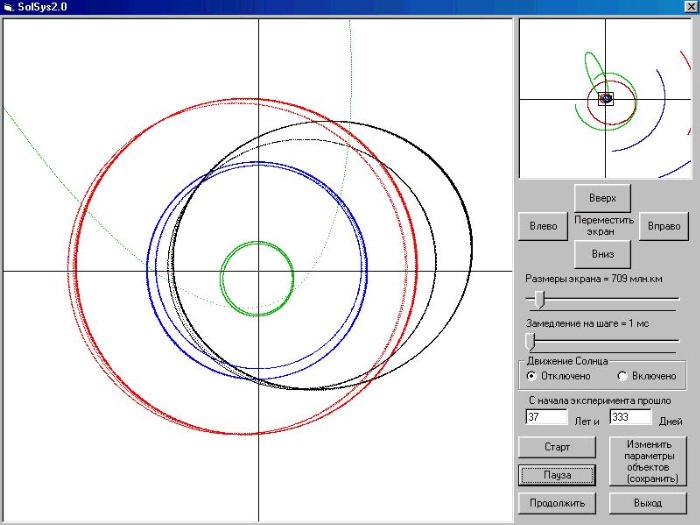
___Масштаб изображения на левом экране можно изменить ползунком, а просматриваемую область пространства выбрать перемещая его влево, вправо, вниз и вверх. При этом на правом экране, который показывает объекты в постоянном масштабе так, чтобы был виден самый отдаленный объект, вы будете видеть квадрат ограничивающий эту область. Также как и на первой форме, чтобы увидеть процесс в замедленном темпе, вы можете ползунком изменить замедление на шаге решения, а чтобы приостановить прцесс вы можете нажать кнопку “пауза”, а затем опять продолжить эксперимент или вернуться к первой форме и сохранить данные в файле. По умолчанию опция “движение Солнца”, отключена, но вы можете ее включить и увидеть, что не только Солнце притягивает планеты, но и они его тоже. После того как вы в нижней части формы увидите сколько лет и дней прошло с начала эксперимента, который будем надеятся закончится для нашей планеты не катострофой, можете нажать кнопку “выход” и отдохнуть от трудов тяжких. А то что это действительно так вы сможете убедится, если не будете изменять на первой форме никакие параметры, а просто начнете эксперимент с начальными данными, и с замиранием будете наблюдать, что происходит с планетами при вмешательстве в их спокойную жизнь постороннего предмета, а именно астероида (правда очень большого). Нажав кнопку <About>, можете ознакомится с работой программы более подробно.
Solsys1.0 - моделирование движения объектов в Солнечной системе.
исполняемый файл Solsys1exe.zip (DOS, 46kb)
исходный файл Solsys1bas.zip (DOS, QBasic, 4kb)
QBasic (Оболочка языка QBasic, 286kb)
____Эта программа является предшественницей программы Solsys2.0 и написана на языке QBASIC для работы под DOS . У нее гораздо меньше возможностей, чем у второй версии, но она включена мною в число программ распространяемых вместе с книгой (исходный файл и распечатка в Word) т.к. является не только примером динамической математической модели механической системы, но и очень полезна в плане обучения программированию т.к. написана на простейшем языке программирования, а цель книги научить читателя моделировать, а не программировать. Но если учесть то, что реализация всех сложных моделей равно как и оптимизация параметров этих моделей подразумевает их машинный вариант, то знание основ программирования просто необходимо.
_____В этой версии вы также можете задать произвольные параметры всех моделируемых объектов, которые по умолчанию даны когда все планеты находятся на оси X в точках перигелия, а вот управление процессом моделирования сведено к минимуму. Вы можете только клавишами < (,) или > (.) изменить масштаб изображения, а клавишей пробел остановить программу. Правда здесь предусмотрен вариант вывода на экран значений параметров объектов в процессе моделирования и вы можете изменить и массы планет. Есть также возможность моделировать движение не всех планет, что значительно ускоряет скорость решения. И если вы, например, укажете, что будете рассматривать только 6 планет, не рассматривая далекие планеты, то значительно ускорите решение, а если этой 6-ой планете (объект Сатурн имеет в программе номер 7) зададите параметры астероида, то сможете также, как и во 2-ой версии наблюдать все катаклизмы от этого вмешательства извне. Задайте параметры Сатурна m = 1111, X0 = 1336, Y0 = 0, VX0 = -6, VY0 = 4 и просто посмотрите что произойдет.
ObsData3 - чтение данных наблюдений за планетами в произвольном формате, их обработка и запись в стандартном формате.
исполняемый файл и примеры данных наблюдений ObsData3minus.zip - (Windows XP-Vista-7, 170 kb)
полная версия программы ObsData3exe.rar - (Windows XP-Vista-7, 7,06 Mb)
копия ObsData3exe.rar на файлохранилище Яндекса - (Windows XP-Vista-7, 7,06 Mb)
копия ObsData3exe.rar на Яндекс диске - (Windows XP-Vista-7, 7,06 Mb)
исходные файлы ObsData3vbp.zip - (Windows XP-Vista-7, Visual Basic 6.0, 160 kb)
ObsData1 - запись данных наблюдений за планетами в стандартном формате.
исполняемый файл и прочие файлы ObsData1exe.rar - (Windows 95-98-XP-Vista-7, 232 kb)
исходные файлы ObsData1vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 53 kb)
отбракованные суммарные данные наблюдений за Солнцем ObsSUMM.zip - (970 kb)
_____ Программа ObsData предназначена для чтения данных наблюдения за планетами и Солнцем, которые записаны в произвольном формате, и для последующей автоматической записи их в одном из стандартных форматов, а конкретно в формате, который используется в Парижском бюро долгот (я его называю формат BDL). Например, дата наблюдения может быть указана как год-месяц-день-часы-минуты-секунды, а может быть указана как год-месяц-день с дробной частью или вообще как юлианская дата (JD), а нам надо записать ее в формате BDL (год-месяц-день-часы-минуты-секунды). Или, например, данные приведены по местному времени и от 12 часов дня, как мы это видим у Леверье, а нам надо их привести к всемирному времени (UT) и как это принято сейчас от 0 часов.
А можно и современные данные, уже записанные в файл, преобразовать из одной системы координат в другую, например, заданные в стандартной эпохе B1950 в эпоху даты или стандартную эпоху J2000, или топоцентрические данные преобразовать в геоцентрические. Или можно упорядочить данные по дате наблюдения, разбить их на несколько файлов или объединить в одном файле из двух, например, с разными датами наблюдений или с данными отдельно по широте и по долготе. Можно и сравнить между собою данные из нескольких файлов или данные из файла с данными, рассчитанными по аналитической теории JPL или численной (эфемериды DE405), а результаты сравнения можно посмотреть или в численном виде или на графике и при этом результаты в численном виде можно также записать в файл вместе со статистикой. А, т.к. в программе уже был режим сравнения данных наблюдения с расчетными данными, то я добавил еще и кнопку для расчета координат планет на произвольную дату по эфемеридам DE405.
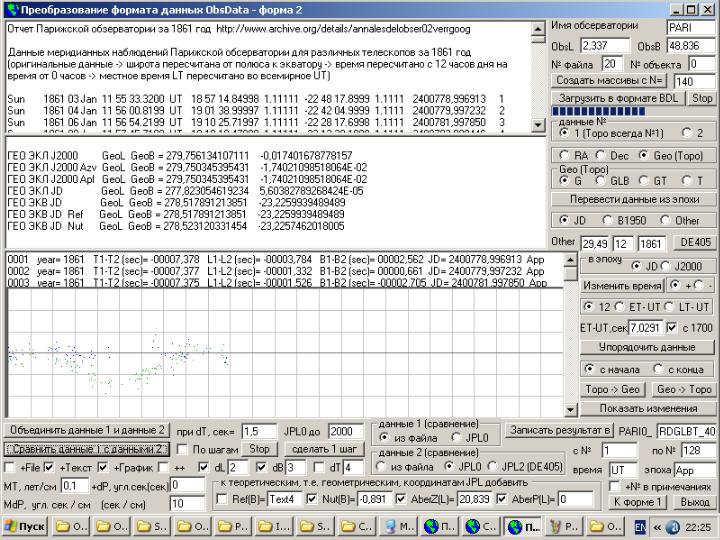
А история написания этой программы такова. Первоначально я сделал программу для чтения данных из таблиц Excel, где они могут быть записаны в произвольном формате, и для последующей записи их в формате BDL, т.к. первыми данными наблюдений за Солнцем, которые я нашел, были данные Николаевской обсерватории http://www.mao.nikolaev.ua/ccd_1/cat_r.php , но они были оформлены в виде таблиц HTML, а моя программа Solsys, на которой я обрабатывал все данные наблюдений, была приспособлена для работы только с данными в формате BDL. Затем я нашел печатный отчет Парижской обсерватории за 1861 год http://www.archive.org/details/annalesdelobser02verrgoog, данные из которого тоже надо было сначала перенести в таблицы Excel. Потом я нашел данные по Солнцу и на сайте НАСА http://iau-comm4.jpl.nasa.gov/plan-eph-data/index.html , где они были записаны в файлах в формате Лаборатории реактивного движения (JPL) и добавил возможность преобразовать данные и из файлов этого формата в формат BDL. А сейчас мне прислали и данные уже в формате BDL http://a-dovgiallo.narod.ru/SUN_1800_1969.rar , которые выложены на сайте Парижского бюро долгот http://www.imcce.fr/host/podb/index.html , но выложены они на FTP сервере без лишней рекламы и по этому узнать о том, что они там есть, можно только тупо просмотрев все папки самому. После этого потребность в этой программе отпала, по этому случись это раньше, то этой программы могло и не быть. Ее могло не быть, по крайней мере в этом виде, и если бы я раньше нашел данные в формате JPL, т.к. на самом деле они у меня давно были, но из-за путаницы JPL с нумерацией планет в этих файлах и в эфемеридах DE405 я не смог их своевременно идентифицировать как данные по Солнцу.
Но как бы там ни было, а первая форма программы ObsData была готова и теперь данные, записанные в произвольной форме, можно было привести к формату BDL, что может быть использовано, например, теми, кто хочет выложить данные своих личных наблюдений на сайте Парижского бюро долгот. Но работать с данными, уже выложенными на сайте Парижского бюро долгот, не очень удобно и я решил создать 2-ю форму для их доработки. Например, данные у них выложены в обратной последовательности, т.е. начиная с самых последних наблюдений, а работать с ними гораздо удобнее в прямой последовательности. Или, например, у них имеется явная ошибка в указание вида времени наблюдения, т.к. кругом указано ET, а как я выяснил должно быть указано UT, что при учете эфемеридной поправки приведет к искажению полученных результатов. А вот анализ одних и тех же данных, но из разных источников, например, обсерватории USNO на сайтах JPL и Парижского бюро долгот или Леверье в его отчете и на сайте Парижского бюро долгот окончательно убедили меня в необходимости создания второй формы программы, т.к. выяснилось, что в одних и тех же данных, опубликованных в разных местах, имеются нестыковки, которые без этой программы даже обнаружить было практически не возможно.
Ну, а, для тех, кого мало интересуют сами данные наблюдений, эта программа может быть полезна в плане программирования, т.к. в тех случаях, когда код может быть полезен в плане обучения программированию, я всегда вместе с исполняемыми файлами выкладываю и исходный код. В данном случае я его выкладываю на языке программирования Visual Basic 6.0. В коде Вы найдете не только примеры работы с файлами последовательного доступа или с таблицами Excel, но и код типовых функций перевода экваториальных координат в эклиптические и обратно, горизонтальных в экваториальные и обратно, из одной эпохи в другую, расчета поправок по рефракции, нутации, параллаксу, звездной и планетной аберрации, перевода календарных дат в юлианские и обратно и многое другое. А кого-то может быть заинтересует алгоритм сортировки данных или простейшая аналитическая теория JPL, по которой можно рассчитывать координаты планет на любую дату. В общем, смотрите сами. А более подробно, как с возможностями программы, так и с порядком работы Вы можете ознакомиться непосредственно при работе программы, нажав кнопку About.
Ptolemey2 - расчет параметров орбиты Земли по продолжительности сезонов года в изложение Птолемея.
исполняемый файл Ptolemey2exe.zip - (Windows 95-98-XP-Vista-7, 20 kb)
исходные файлы Ptolemey2vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 14 kb)
______Программа Ptolemey предназначена для расчета по продолжительности сезонов года (весны и лета) параметров орбиты Земли. Птолемей для отражения видимого неравномерного движения Солнца вокруг Земли использовал теорию простого эксцентра Гиппарха, которая идентична теории движения эпицикла по дифференту. Суть этой теории состоит в том, что Солнце движется равномерно по эксцентру, который смещен относительно центра мира, где находится Земля на величину эксцентриситета эксцентра OT.
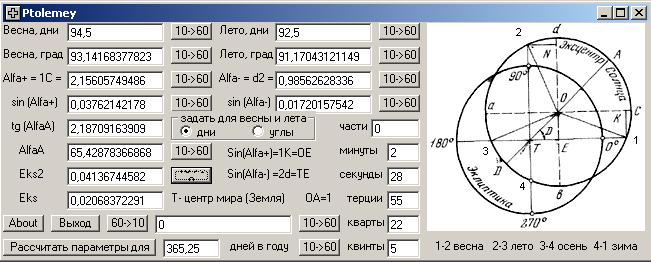
Теперь, наблюдая из центра эклиптики (мира) T, где находится Земля, за движением Солнца, мы увидим, что в точке афелия Солнца (A) оно движется медленнее, чем в точке перигелия (D). Если мы говорим о гелиоцентрической орбите Земли вокруг Солнца (при движение по кругу эклиптики), то будет происходить тоже самое, только в точке (A) будет находиться перигелий Земли, а в точке (D) афелий. На рисунке точкой 1 отмечена точка весеннего равноденствия (начало сезона весны), точкой 2 момент летнего солнцестояния (начало лета), точкой 3 осеннее равноденствие (начало осени) и точкой 4 зимнее солнцестояние (начало зимы).
Расчет положения афелия Солнца и эксцентриситета эксцентра начинается с того, что мы переводим, исходя из продолжительности года, продолжительность сезонов весны (дуга 1-2) и лета (дуга 2-3) в градусную меру. Например, для данных Гиппарха это будет 93,14 и 91,17 градусов. Теперь находим сумму этих углов, вычитаем из нее 180 градусов и делим пополам. Получается 2,156 градуса. Это дуга 1-C. Теперь из угла весны вычитаем угол 90 градусов и найденную дугу 1-C. Получится дуга d-2 равная 0,986 градуса. Если принять радиус эксцентра равным единице, то в этом масштабе отрезки 1-K=O-E и 2-N=T-E будут равны синусам найденных двух дуг.
Теперь по теореме Пифагора можем найти гипотенузу T-O, которая и будет равна эксцентриситету эксцентра. А, зная все три стороны треугольника TOE, используя любую тригонометрическую функцию, найдем угол 1TA, т.е. долготу афелия. А, т.к. все данные у древних астрономов приведены в шестидесятиричной системе счисления, я оснастил программу функцией перевода этих данных в привычную нам десятиричную систему счисления (кнопка 60->10) , а все данные, полученные в программе в десятиричной системе можно для сравнения с расчетом древних астрономов перевести в шестидесятиричную систему счисления (кнопки 10->60).
Savosta1 - моделируется поступательное движение вращающегося диска с двумя массами закрепленными на нем упругими элементами.
исполняемый файл Savosta1exe.zip - (Windows 95-98-XP-Vista-7, 36 kb)
исходные файлы Savosta1vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 20 kb)
Основное назначение программы Savosta
продемонстрировать,
как из реальных сил инерции при вращательном движение возникает
фиктивная
центробежная сила, которая может быть использована как аналог сил
инерции поступательного движения при решении простейших задач с
вращающимися телами, а побочное назначение показать, что при любых
скоростях
движущегося поступательно и вращающегося диска не возникает поперечного
дисбаланса центробежных сил, который бы приводил, как пишет в своей
статье
Савоста, к возникновению, так называемой, поперечной силы.
http://scicommunity.ru/index.php/materials/nauchnye-trudy/112-savosta-v-s-o-zakone-poperechnoj-sily-dejstvuyushchej-na-vrashchayushchiesya-tela-pri-ikh-postupatelnom-dvizhenii-v-svobodnom-prostranstve-vakuume
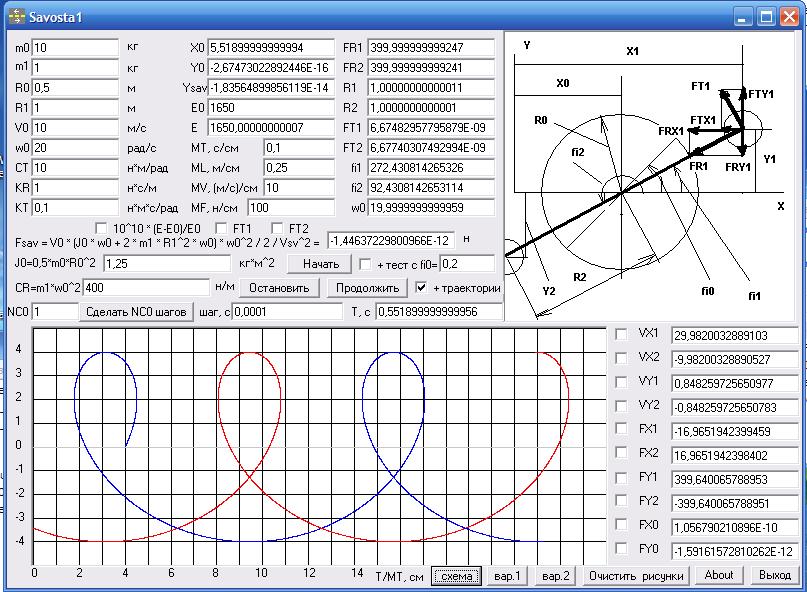
FR=CR*R+KR*VR
где VR это скорость изменения радиуса (деформации пружины), а KR это коэффициент жидкостного трения. В принципе, наличие последнего члена в этой формуле не обязательно и в самой конструкции этот демпфер может отсутствовать, но для более стабильного решения дифференциальных уравнений численными методами я всегда добавляю в уравнения силы демпфирования. Но, если они Вам так не нравятся, то можете задать в исходных данных KR=0, и никаких сил демпфирования не будет.
Аналогично, зная угол поворота fi0 места крепления упругого элемента CT на диске и угловое положение масс m1 и m2, т.е. углы fi1 и fi2, находим углы закрутки упругих элементов Dfi1 и Dfi2, а потом по формуле
FT=(CT*Dfi+KR*VT)/R
находим тангенциальную силу, действующую на массы m1 и m2, где аналогично KT это коэффициент жидкостного трения в упругом элементе, а VT это угловая скорость закрутки упругого элемента. При этом силы FT1 и FT2 будут не только (с обратным знаком) действовать на массу m0, но и создавать крутящий момент (с обратным знаком), который будет замедлять вращение диска.
Теперь раскладываем эти силы FR и FT по осям X и Y и находим, используя 2-ой закон Ньютона, ускорения масс m0, m1 и m2 по осям X и Y, а, зная крутящий момент, приложенный к диску, находим его угловое ускорение. Таким образом, вращательное движение масс m1 и m2 вокруг диска с массой m0 моделируется только как поступательное движение масс m1 и m2 по осям X и Y, т.е. тут не может быть никаких центробежных сил, а возникают только силы инерции, которые пытаются сохранить прямолинейное движение, но при этом увеличивают расстояние между массами m1 и m2 и массой m0 , что приводит к увеличению радиальной силы растягивающейся пружины и эта сила изменяет направление движения масс m1 и m2, заставляя их не улетать далеко от массы m0, а в конечном итоге двигаться вокруг нее на одном и том же расстоянии.А вот в окошке <Ysav> у нас будет выводиться ордината диска, которая должна у него быть на данный момент времени, если бы на него действовала сила Fsav. Как не трудно убедиться, сравнив эту ординату Ysav с получающимся значением Y0, никакой боковой силы Савосты не существует, т.е. центробежная сила, действующая на 1-ый и 2-ой грузы, когда они расположены перпендикулярно скорости движения, будет одна и та же. Это легко объясняется, если мы посмотрим на траектории движения этих масс в этих положениях (смотрите скриншот программы), из которых видно, что у левого груза радиус кривизны будет меньше, а у правого больше, что при разных линейных скоростях дает одинаковое значение фиктивной центробежной силы.
Runge2.0 - решение дифференциальных уравнений описывающих движение материальной точки по одной координате или по двум численными методами Эйлера или Рунге-Кутта
исполняемый файл Runge2exe.zip - (Windows 95-98-XP-Vista-7, 36 kb)
Данная программа позволяет численными методами Рунге-Кутта по 4-м коэффициентам или Эйлера решать дифференциальные уравнения описывающие движение материальной точки (по одной или двум координатам) при воздействии на нее различной внешней силы и при различных видах "упругой силы" удерживающей эту точку от смещения относительно начала координат.
Внешняя сила Fw
может быть задана в одном из трех
вариантов Fw=F0*Sin(w0*T), Fw=F0*Cos(w0*T) и Fw=F0,
где F0 - максимальное значение внешней
силы
w0 - частота изменения внешней силы
T - время
Движение материальной точки может
осуществлятся как по одной
координате, т.е. вдоль линии так и по
двум, т.е. в плоскости. При этом сила
Fk, которая удерживает нашу точку
относительно начала координат,
может быть задана в 4-х вариантах Fk=0,
Fk=-k*x, Fk=kq*qe*qp/R^2 и Fk=-sgn(x)*k*x^2, где
k - коэффициент пропорциональности
силы удерживающей нашу
материальную точку от смещения
относительно начала координат или
относительно протона находящегося
первоначально в начале координат
если нашей точкой является
электрон вращающийся вокруг
протона (в простейшем случае когда
Fk=-k*x коэффициент k равен жесткости
обычной пружины).
qe,qp - заряд соответственно
электрона и протона
kq - коэффициент пропорциональности
в формуле Кулона
x - расстояние от центра координат
до материальной точки при движении
вдоль одной координаты
R - расстояние от протона, который
первоначально находится в центре
координат, до электрона при
движении по "окружности", т.е.
по двум координатам.
Значения
вышеназванных параметров k, F0, w0, R0, qe
а также начальную скорость точки V0
и ее массу m можно задать в
текстовых окошках. А если Вы хотите
задать начальные параметры
электрона (R0, V0) соответствующие
определенной частоте его обращения
вокруг протона, то можете задать их
автоматически нажав кнопку <L0=f(n,k)>.
При этом частота обращения
электрона вокруг протона wv будет
соответствовать длине волны
излучения посчитанной по формуле
Ридберга L0=1/RL/(1/n^2-1/k^2) с заданными
Вами коэффициентами n и k или
заданной Вами произвольной длине
волны, если в окошке <n> будет
введен ноль. При этом будут
расчитаны не только длина волны
излучения L0 и соответствующая ей
частота обращения электрона wv, но и
требуемый для этого коэффициент
пропорциональности k для формулы по
которой будет определятся упругая
сила и собственная частота
колебаний электрона на упругом
элементе wk при радиусе равном R0.
Прежде, чем
начать вычислительный эксперимент,
Вам надо будет так же задать еще
несколько масштабов для вывода
данных на два экрана. Это масштаб
линейных размеров Mx, масштаб
времени для осциллограммы Mt,
масштаб изменения суммарной
энергии системы (кинетическая плюс
потенциальная), а так же задать шаг
решения в секундах и сам метод
численного решения
дифференциальных уравнений. А для
того, чтобы Вы могли проверить
правильность работы программы, я
для простейшего движения по одной
координате, когда сила Fk=0, сделал
вывод на нижний экран одновременно
координаты X точки как при
численном решении, так и при
аналитическом.
Во время
проведения вычислительного
эксперимента Вы будете не только
наблюдать на правом экране
реальное перемещение материальной
точки в масштабе Mx, но и увидите в
том же масштабе изменение
координаты X или расстояния от протона до электрона R (синяя линия)
на осциллограмме (нижний экран). Там
же внизу экрана Вы увидите (зеленая
линия) график изменения внешней
силы Fw и график изменения суммарной
энергии (кинетическая плюс
потенциальная) нашей материальной
точки (красная линия), а при
варианте возможности перемещения и
протона график изменения суммарной
энергии системы электрон-протон.
Кроме вывода на экраны показателей
проводимого эксперимента, часть из
них выводится и в численном виде в
текстбоксах расположенных слева от
верхнего экрана, а если Вы включите
чекбокс <Запись>, то данные будут
еще записываться и в файл.
Конкретно выводятся следующие
показатели
X,Y - координаты точки
wT - экспериментальное значение
частоты обращения электрона вокруг
протона (при незначительных
колебаниях радиуса вращения
электрона wT должно быть равно
теоретическому значению wv)
R - расстояние от электрона до
протона (центра координат)
V - линейная скорость электрона
mc - эффективная масса электрона с
учетом преобразований Лоренца mc=m/(1-V^2/Vc^2),
где Vc = 299780 км/сек - скорость света
FkX - проекция силы упругого элемента
на ось X, т.к. сила Fk при обращении
электрона вокруг протона
раскладывается на две силы FkX и FkY
для расчета ускорений электрона и
протона при решении
дифференциальных уравнений как по
оси X так и по оси Y.
dEp,dEk,dE - соответственно изменение
потенциальной, кинетической и
суммарной энергии материальной
точки (системы электрон-протон) от
начальных значений, т.е. значений в
начале эксперимента. Изменение
кинетической энергии электрона
определялось по формуле dEk=(mc*V^2-m*V0^2)/2,
а изменение потенциальной энергии
определялось для различных упругих
элементов по своим формуламулам
для каждого элемента dEp(R)=k*(R^2-R0^2)/2, dEp(R^-2)=k*(1/R0-1/R)
и dEp(R^2)=k*(R^3-R0^3)/3
T - текущее время.
Alfa - угол на который повернулся
электрон при движении вокруг
протона при возрастании угла
против движения часовой стрелки.
Hrono2 - усовершенствованная версия программы Hrono1
исполняемый файл Hrono2exe.zip - (Windows 95-98-XP-Vista-7, 52 kb)
_____По сравнению с программой Hrono1 добавлена проверка еще 2-х вариационных принципов и убрана проверка принципов кратчайшего времени Ферма и Бернулли. Но появилась возможность в поле ))var2- задать скорость перемещения второму источнику поля, а также можно в нем смоделировать движение и по трем координатам.Hrono1R - усовершенствованная версия программы Hrono1, в которой добавлена возможность проверять принцип наименьшего действия и в релятивистской форме.
исполняемый файл Hrono1Rexe.zip - (Windows 95-98-XP-Vista-7, 88 kb)
_____По сравнению с программой Hrono1 добавлены только несколько окошек для вывода замедления (ускорения) времени при движение тела в гравитационном поле и с учетом эффекта от преобразований Лоренца от скорости, а начальные данные заданы для решения так называемой задачи Фейнмана с полетом ракеты.
Hrono1 - моделирование движения тела в различных силовых полях и луча света в слоистой среде
исполняемый файл Hrono1exe.zip - (Windows 95-98-XP-Vista-7, 84 kb)
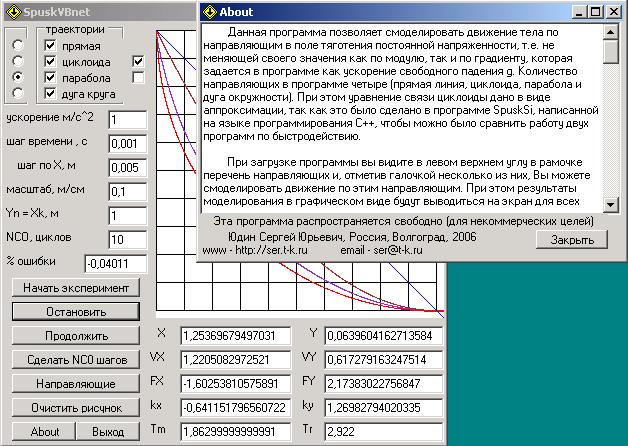
_____Данная программа не только позволяет смоделировать движение одной массы в поле тяготения создаваемом другой массой с большим выбором как вида поля так и вида движения, но и с помощью дополнительных расчетов экспериментально опровергнуть справедливость принципа кратчайшего времени Ферма и принципа наименьшего действия Мопертюи, а также просто углубить свои познания по основным законам физики.

______В программе предусмотрено как свободное движение тела, так и несвободное с 4 уравнениями удерживающих связей (прямая, циклоида, парабола и дуга окружности), которые можно задать в рамке <траектории> (можно задать сразу все - при этом будет одновременно моделироваться движение нескольких разных масс m1 по всем заданным траекториям). Кроме этого мы можем задать постоянные внешние силы Fx и Fy действующие на нее, а также ее начальные скорости VX и VY.
_______Программа позволяет смоделировать 10 видов только монополей и нажав кнопку <Показать траектории>, Вы, кроме траекторий, увидите в левом верхнем углу правого рисунка характер изменения напряженности выбранного Вами поля, а для свободного движения в поле ))var2- предусмотрена возможность движения массы 1 сразу в двух полях. Примеры свободного движения в монополях ))var1- и ))var2- даны на среднем рисунке под окном программы, а в монополях ))var1+ и ))var2+ даны на правом рисунке.
______При проведении вычислительного эксперимента решение дифференциальных уравнений , описывающих движение массы 1, производится методом Рунге-Кутта по 4-м коэффициентам и траектория этого движения в масштабе Mx изображается на правом рисунке, а в масштабе M, выбранные Вами показатели движения, отображаются на осциллограмме (нижний рисунок) с разверткой по времени в масштабе Mt. При этом под правым рисунком мы можем наблюдать численное значение этих показателей, а конкретно
X, Y - текущие
координаты
VX, VY - проекции скоростей по осям X и Y
Fm - сила гравитационного притяжения,
например, в поле ))var2- Fm=66.7*10^-12*m1*m2/LR/LR
Fq - сила электростатического
взаимодействия, например, в поле ))var2-
Fq=9*10^9*q1*q2/LR/LR
Fj1 - сила жидкостного трения внутри
массы 1 Fj1=Kj1*VR1, где VR1- текущая
скорость упругой деформации массы 1
Dfi - точность определения
численными методами интервала угла,
где находится на циклоиде масса 1
Lmax - расстоянее, которое прошла
масса 1 от начальной точки до
конечной при выполнении выбранного
условия в рамке <Tmax>
EС1- потенциальная энергия упругой
деформации массы 1
Ev- кинетическая энергия
поступательного движения массы 1
E- полная энергия как запасенная
системой так и рассеянная в ней за
время проведения вычислительного
эксперимента
Em- потенциальная энергия массы 1 от
силы гравитационного притяжения
относительно нулевого уровня
Eq- потенциальной энергии массы 1 от
сил электростатического
притяжения или отталкивания
относительно нулевого уровня
Ej1- энергия рассеянная внутри массы
1 от сил жидкостного трения с
коэффициентом Kj1 при ее колебаниях
на направляющей за счет упругой
деформации этой массы.
E0- суммарная энергия массы 1 до
начала эксперимента
____Для проверки принципа
кратчайшего времени Ферма наш рисунок (имеющий размеры 20*20
метров) разобит на 20 горизонтальных
слоев имеющих различный
коэффициент преломления света и из
левого верхнего угла рисунка
вылетают два луча света, которые
пройдя верхний слой, далее движутся
согласно закону преломления. Один
из примеров такого движения дан на
левом рисунке под окном программы.
При этом Вы можете использовать,
как установленное по умолчанию
изменение коэффициента
преломления по слоям, так и задать
закон его изменения в виде K=1+Dn*(i-1)
или K=1+Dn*(i-1)^2 в зависимости от того
какой показатель степени 1 или 2 Вы
зададите в рамке <Степень> и
какой знак и величину зададите
параметру Dn. После прохождения
каждого слоя в текстовых окошках
под рисунком Вы увидите следующие
параметры
Fm, Fq - номер слоя для левого и
правого лучей, на начале которого
они закончили свое движение
Fj1, Dfi - абсцисса, где лучи закончили
движение
Lmax, EС1 - углы преломления лучей, т.е.
углы под которыми лучи будут
двигаться в следующем слое или в
этом же, где они двигались сейчас,
если отразяться
Ev, E - синусы этих углов
Em, E0 - скорость движения света в слое,
который он прошел.
Eq, Ej1 - время, которое луч прошел от
начала движения до точки, где он
остановился.
____Для проверки принципа
наименьшего действия, а заодно и
утверждения, что циклоида является
брахистохроной, в программе
имеются 25 текстовых окошек
расположенных в центре формы. В
первой колонке выводятся значения
времени движения массы 1 (T1...T5) от
точки с координатами Xn, Yn до точки с
координатами Xk, Yk для каждой из
выбранных для эксперимента
траекторий. При этом время
замеряется при достижении или Xk или
Yk в зависимости от условия которое
Вы зададите в рамке <Tmax>. А в
четырех следующих колонках
выводятся интегральные или средние
за эксперимент значения
произведения массы 1 на ее скорость,
ее кинетической энергии и суммы или
разности кинетической энергии и
потенциальной. Если у Вас рядом с
показателем стоит галочка, то
выводятся средние за эксперимент
значения, а если нет то
интегральные. Причем как средние,
так и интегральные показатели
выводятся как по времени, так и по
пути в зависимости от того какой
переключатель у Вас включен в рамке
<Интеграл>. Кроме того, поставив
галочку у одного из показателей, Вы
можете вывести этот показатель на
осцилограмму, также как и для
показателей находящихся под правым
рисунком.
Udar3 - моделирование удара двух шаров с произвольными параметрами или шара с произвольными параметрами и абсолютно жесткого стержня
исполняемый файл Udar3exe.zip - (Windows 95-98-XP-Vista-7, 42 kb)
____Эта программа является модернизированной версией программы Udar23 в которой добавлена возможность смоделировать удар шара в стержень, но в упрощенном виде, т.к. шар берется с упруго-диссипативными параметрами, а стержень абсолютно жесткий и при этом в расчетах не учитывается энергия пошедшая на трения в пятне контакта шара со стержнем. Сделаны и некоторые мелкие усовершенствования, например, в программе стало более удобно задавать начальные параметры шаров такие как начальные координаты и стало возможным самому задавать все масштабы а также теперь можно выбирать какие параметры выводить на осциллограмму. Подробное описание программы читайте в ее About.
Udar2.3 - моделирование удара двух шаров с произвольными параметрами
исполняемый файл Udar23exe.zip - (Windows 95-98-XP-Vista-7, 40 kb)
_____Программа Udar23 позволяет смоделировать удар двух тел с любыми параметрами и под любым углом и, следовательно, ударяющимися телами могут быть не только объекты нормальных размеров, но и планеты и элементарные частицы. Например, Вы можете экспериментально проверить, что позитрон, даже при скорости равной 99.9% от скорости света никогда не долетит до протона, или можете наблюдать интересное явление, когда отрицательный мю мезон (при определенных параметрах), сталкиваясь с протоном, отлетает от него на некоторое расстояние, а затем окончательно притягивается к протону. Программа написана на языке Visual Basic 6.0 и является усовершенствованной версией программы Udar1, написаной на языке QBasic. Для того, чтобы начать вычислительный эксперимент, Вам надо задать следующие параметры ударяющихся тел (далее шаров)
m10, m20- массы покоя
шаров
q1, q2- заряды шаров
D1, D2- диаметры шаров
C1, C2- жесткость шаров
Kj1, Kj2- коэффициенты жидкостного
трения внутри шаров
Ks- коэффициент сухого трения
поверхностей шаров друг о друга
VX1, VX2- скорости шаров по оси X
VY1, VY2- скорости шаров по оси Y
X1/D1, X2/D1- координаты шаров по оси X в
долях D1 в предпологаемом месте
удара
Y1/D1, Y2/D1- координаты шаров по оси Y в
долях D1 в предпологаемом месте
удара
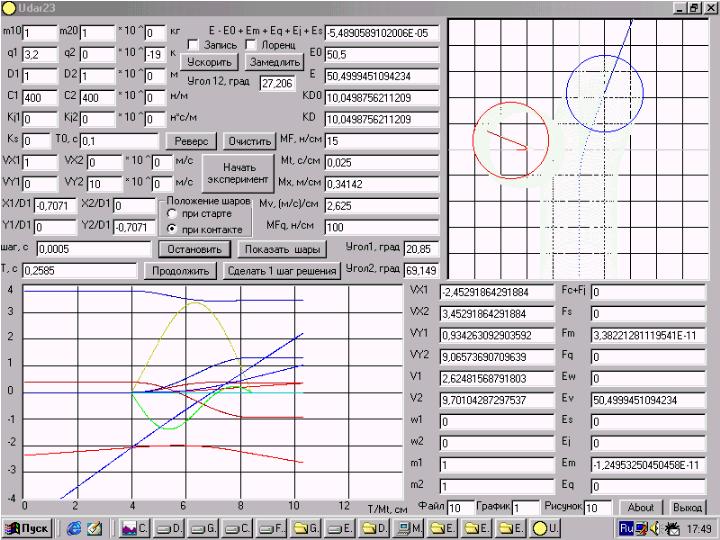
____Во время вычислительного эксперимента Вы наблюдаете на правом рисунке не только сами перемещения шаров, но и векторы их скоростей и траектории их движения . При этом на левом рисунке в том же масштабе, который указан слева от правого рисунка, Ва видите осциллограмму на которой выводятся значения координат и скоростей шаров по осям X и Y, а также проекции суммарной силы взаимодействия между шарами по тем же осям и отдельно силу электростатического взаимодействия в масштабах, которые так же указаны слева от верхнего рисунка. Значения проекций скоростей выводятся также в числовом формате под правым рисунком, где выводятся также текущие значения угловых скоростей шаров и их масс, а если включена опция <Лоренц>, то массы шаров изменяются с учетом преобразований Лоренца. Там же выводятся текущие значения сил взаимодействия и различные виды энергий системы.
Fc+Fj - сила
взаимодействия между шарами от
действия сил упругости шаров Fc и
диссипативных сил Fj, например, со
стороны 1-го шара будет действовать
сила F1=C1*(R1-R10)+Kj1*VR1, где VR1- текущая
скорость деформации первого шара
Fm=66.7*10^-12*m1*m2/LR/LR - сила
гравитационного притяжения между
шарами
Fq=9*10^9*q1*q2/LR/LR - сила
электростатического
взаимодействия между шарами
Fs=Ks*(Fc+Fj+Fm+Fq)*Sqn(Vs) -сила трения
движения между поверхностями шаров,
где Vs-скорость скольжения шаров
Ev- кинетическая
энергия системы от поступательного
движения шаров
Ew- кинетическая энергия системы от
вращательного движения шаров
Es- энергия системы рассеянная при
сухом трении на поверхностях шаров
Ej- энергия системы рассеянная при
жидкостном трении внутри шаров
Em- уменьшение потенциальной
энергии системы при сближении
шаров на величину работы совершенной
силой гравитационного притяжения.
Eq- уменьшение или увеличение
потенциальной энергии системы на величину работы совершенной силой
электростатического притяжения
или отталкивания при сближении или
удалении шаров.
Над левым
рисунком Вы также видите текущее
время T, уголы между осью абсцисс и
направлениями скоростей шаров (угол1
и угол2) и между осью абсцисс и
линией соединяющей центры масс
шаров (угол12), а также заданный Вами
шаг решения дифференциальных
уравнений. Включив опцию <Запись>,
Вы можете записать все текущие
параметры в файл, а нажав кнопку
<About>, ознакомится с работой
программы более подробно.
Krivoship1 - создание математической модели кривошипно-шатунного механизма различными методами получения дифференциальных уравнений.
Krivoship1exe.zip - (Windows
95-98-XP-Vista-7, 44 kb)
Данная программа позволяет
продемонстрировать на конкретном
примере, а именно на кривошипно-шатунном
механизме (КШМ) возможности
различных методов (методик)
получения дифференциальных
уравнений описывающих с
математической точки зрения
поведение различных физических
систем, т.е. различных
математических моделей (ММ) этих
систем, которые затем решаются на
компьютере численными методами (конкретно
в этой программе методом Рунге-Кутта
по 4-м коэффициентам). В данной
программе планируется описание КШМ
с применением уже исвестных
методов (методик) а именно с
использованием уравнений Лагранжа
1-го и 2-го рода, принципа возможных
перемещений и предлогаемого мною
метода, который является модифицированным принципом
Даламбера. Сейчас в программе
реализованы метод с использованием
уравнений Лагранжа 2-го рода и
предлагаемый мною, хотя в этой задаче он аналогичен классическому принципу Даламбера.
В современных
учебниках принцип
Даламбера излагается только как баланс сил, но в моем прочтение
он мне видиться как баланс мощностей (хотя в то время, когда он
был сформулирован, еще не
существовало таких понятий как
мощность или энергия). И хотя 99%
систем можно описать используя
только уравнения сил, всегда надо помнить,
что такое преобразование уравнения
мощностей в уравнение сил
происходит только в том случае,
когда у нас в системе строго задано
кинематическое согласование
скоростей отдельных элементов
системы. А, например, при работе
клиноременной передачи или при
качение колеса автомобиля такое
строгое кинематическое
согласование скоростей не может
быть задано, т.к. наблюдается
упругая пробуксовка (не говоря уже
о неупругой) и по этому необходимо
обязательно использовать только
уравнение мощностей. В то же время, следует отметить, что у уравнение
мощностей тоже является частным случаем уравнения сил, если действующие
на элементы системы силы не совпадают по направлению со скоростью
перемещения этих элементов, что также встречается в 99%
систем .
По этому, в каждом конкретном случае надо для описания движения одних
элементов системы применять уравнение мощностей, а для других
уравнение сил.
Другим отличием предлагаемой мною
методики от существующих, т.к. она
сразу создавалась под компьютерную
реализацию созданных ММ, является
то, что для определения усилий между элементами системы не
все элементы системы при ее
описание принимаються абсолютно
жесткими, а часть из них, как и
реальные элементы, принимаются
обладающими упруго-диссипативными
свойствами. При этом как упругие
так диссипативные свойства этих
элементов могут быть самыми
разнообразными и определяются
исходя из конкретной конструкции
механизма и отдельных его
элементов. В данном абстрактном КШМ
я наделил податливостью, величина
которой задается в программе как
жесткость соединений kF (величина
обратная податливости, т.е.
коэффициенту пропорциональности
деформации приложенной силе),
соединения элементов КШМ (шарниры).
А для того, чтобы повысить
устойчивость решения и сгладить
колебания в системе в начале
эксперимента, когда не все
начальные параметры заданы точно, я
наделил соединения еще и свойством
демпфировать колебания, т.е. принял,
что при деформации элементов
соединения будет возникать не
только сила упругости, но и сила
жидкостного трения
пропорциональная скорости
деформации элементов соединения и
коэффициенту жидкостного трения kj,
хотя на самом деле трение будет
более сложным. При этом, если упруго-демпфирующие
свойства конкретного элемента
конструкции заданы в ММ как
фиктивные, то надо стремиться
подобрать эти параметры так, чтобы
энергия рассеянная при трение была
минимальна и не превышала за время
проведения вычислительного
эксперимента долей процента
от общей энергии системы (хотя в
реальных элементах систем
рассеивание энергии может быть
гораздо больше).
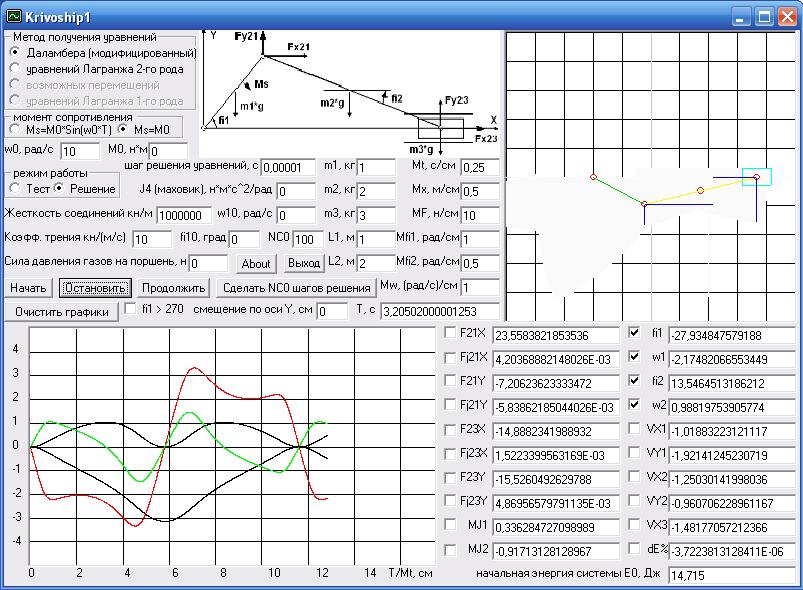
При загрузке программы, Вы в левом
верхнем углу в рамке <Метод
получения уравнений> выбираете
метод с помощью которого получены
дифференциальные уравнения,
описывающие работу КШМ, и затем,
задав параметры этого механизма и
внешние воздействия на него, видите
на экране монитора, то, что Вам
данный метод может дать при решение
численными методами уравнений,
полученных с использованием этого
метода. Но, прежде чем нажать кнопку
<Начать> Вы, кроме задания шага
решения уравнений, должны задать
конкретные параметры КШМ, а именно
массу кривошипа - m1, массу шатуна - m2,
массу поршня - m3, длинну кривошипа - L1
и длинну шатуна - L2. Кроме этого, Вы в
рамке <момент сопротивления>
выбираете различные режимы
изменения момента сопротивления Ms,
который может быть задан в одном из
двух вариантов Ms=M0*Sin(w0*T) и Ms=M0, а
также уточнить различные масштабы
вывода показателей работы на экран
в графическом виде. Кроме того, Вы
можете задать начальную скорость
вращения кривошипа w10 и момент
инерции маховика J4 (при его наличие).
А если Вы собираетесь проводить
вычислительный эксперимент на
математичемкой модели КШМ,
уравнения которой получены с
применением предлагаемой мною
методики, то Вам надо еще уточнить
жесткость соединений для
определения упругой силы в
соединениях КШМ и коэффициент
жидкостного трения для определения
силы жидкостного трения в
соединениях. И так как у
большинства КШМ наверное
ассоциируется с двигателем
внутреннего сгорания, я
предусмотрел и возможность задать
силу давления газов на поршень при
их горение Fr, т.е. при рабочем ходе
поршня. При этом для простоты
принято, что сила давления газов на
поршень при сжатие газов Fs равна 20%
от силы давления при рабочем ходе, а
двигатель у нас двухтактный, т.е.
весь рабочий цикл совершается за
один оборот кривошипа.
Предлагаемая мною методика
получения ММ систем позволяет не
только получить все показатели
работы исследуемой системы, а не
только кинематические, как в ММ
полученной с помощью уравнений
Лагранжа 2-го рода, но и
автоматически воспроизводит все
эффекты, которые могут происходить
в реальном объекте, например,
явления резонанса. Так как для
математического описания систем я
использую Декартову систему
координат, то у меня для описания
КШМ получается 5 дифференциальных
уравнений второго порядка, решая
которые, мы можем получить кроме
угла поворота кривошипа и угла
поворота шатуна относительно его
центра масс также перемещения
центра масс шатуна по осям X и Y и
перемещение центра масс поршня по
оси X, а также скорости их
перемещений по этим координатам.
Кроме этого ММ созданная по моей
методике позволяет получить все
усилия возникающие в элементах
конструкции и все энергетические
показатели работы моделируемой
системы.
При заданных в программе по
умолчанию параметрах жесткости
шарниров и коэффициента трения в
них процент ошибки решения по
энергии системы потерянной на
трение в шарнирах при обычных
скоростях вращения кривошипа не
превысит и сотых долей процента. Но
в некоторых конструкциях
податливости элементов этих
конструкций могут оказаться очень
значительными и если коэффициент
трения будет задан как фиктивный,
то это может привести к
значительным фиктивным потерям
энергии в системе и процент ошибки (по
энергии) может быть не допустимо
большим, по этому внимательно
следите за этим показателем на
осциллограмме. Численные методы
решения конечно же тоже будут
вносить погрешность в решение, но
при правильно заданных параметрах
эта погрешность также не превысит
сотых долей процента. А вот
упрощение реальных систем для
более удобного их математического
описания может дать десятки
процентов ошибки и даже
незначительное с математической
точки зрения допущение, которое
сделано в файле Krivo2.mws при
нахождение cos(fi2) при упрощенном
выводе дифференциального
уравнения описывающего КШМ с
помощью уравнения Лагранжа 2-го
рода и которое используется в этой
программе, приводит к ошибке +/- 1%
даже при свободных колебаниях КШМ.
Поэтому мнение о том, что
аналитическое решение задачи
всегда точнее чем ее решение
численными методами является
большим заблуждением. А если к
этому добавить, что практически ни
одна реальная задача не может быть
решена аналитически без
значительных упрощений
рассматривамой системы и допущений
при математических выкладках, то
предлагаемый мною метод
математического описания
механических систем является
реальной альтернативой
существующим методам
докомпьютерной эры. Моя методика,
не требующая ни упрощения систем ни
допущений при математических
выкладках, позволяюет создать
именно модель системы, а не
квазимодель, пригодную только для
решения простейших учебных задач. И
хотя моя методика практически
пригодна только для
математического описания систем с
последующим решением уравнений
численными методами на цифровых
ЭВМ это никоим образом не может
быть ее недостатком, т.к. сегодня
компьютеры это не экзотика. Тем
более, что простейшие системы,
например, удар двух шаров, могут
быть не только описаны с помощью
этой методики, но полученные
уравнения могут быть и решены
аналитически, как я это сделал в
своей статье <Две меры
механической формы движения
материи>, где приведено
аналитическое решение для упругого
и неупругого удара двух шаров,
которое мною получено впервые (по
крайней мере я этого решения нигде
не встречал), хотя данная задача и
является классической.
Кого интересуют подробности,
предлагаемой мною методики, могут
ознакомиться с ними в моей книге по
моделированию систем, а данная
программа просто демонстрирует
возможности различных методов
математического описания
физических систем. А с методикой
получения дифференциального
уравнения с использованием
уравнений Лагранжа 2-го рода можно
ознакомиться, скачав файлы Krivo1 и Krivo2
для пакета Maple9.5 (просто посмотреть
эти файлы без проведения
вычислений можно браузером в
формате html).
KrivoMWS.zip - (Windows
95-98-XP-Vista-7, Maple9.5, 34 kb)
KrivoHTML.rar - (Windows
95-98-XP-Vista-7, Internet Explorer, 306 kb)
Plank5.0 - построение различных статистических распределений и подбор методом многофакторного планирования коэффициентов для распределения Планка.
исполняемый файл Plank5exe.zip - (Windows 95-98-XP-Vista-7, 56 kb)
Данная программа позволяет с другой стороны взглянуть на физическую сущность формулы Планка (как типичного статистического распределения) и которая может быть получена практически из любого статистического распределения путем подобора соответствующих коэффициентов. А применение методов многофакторного планирования позволяет опытным путем подобрать коэффициенты для этой формулы.
Конкретно
программа позволяет построить
распредедения Больцмана, Релея,
Планка и Гаусса (нормальное
распределение), а также их
комбинации, которые строятся в
функции от частоты излучения и
поэтому надо задать масштаб Mv, в
котором будет откладываться по оси
X частота излучения, а
распределение Планка можно
построить и в функции длинны волны
излучения. Распределение Максвелла
строится в функции скоростей
молекул газа и поэтому для него в
окошке <Vmax> надо указать
скорость которая будет
соответствовать координате X=20 см.
При этом по оси Y для распределения
Планка необходимо задать в окошке
<Mr(v)> масштаб удельной мощности
излучения приходящейся на
бесконечно маленький интервал
изменения частоты излучения v. А для
всех остальных распределений
масштаб по оси Y задается
автоматически и его значение
выводится в окошке <MP(x)>. Хотя и
для них его можно задать
принудительно в этом же окошке
отметив галочкой чекбокс <Задать
MP(x)>. Кроме этого для
распределения Максвелла, также как
и для распределения Планка, надо
задать температуру молекул газа в
окошке <k4(T)>, и массу одной
молекулы в окошке <m0>. Для
построения нормального
распределения надо задать частоту
излучения на которую приходится
матожидание плотности вероятности
в долях от максимального значения
частоты в окошке <msr> и величину
дисперсии вероятности в долях от
матожидания в окошке <sigma=msr/>.
Нажав кнопку <R=f(v),f(L)>
можно увидеть несколько
стационарных орбит вращения
электрона по Бору и расчет частоты
излучения при переходе электрона с
одной орбиты на другую, когда
частота излучения расчитывается по
методике Бора как разность от
энергий электрона на двух
стационарных орбитах деленная на
постоянную Планка h. Кроме этого для
этих орбит выводятся абсолютные
значения энергии электрона на этих
орбитах а также частота вращения
электрона на этих орбитах и
соответствующая ей длина волны
излучения если предположить, что
частота излучения равна частоте
обращения электрона на орбите. Из
этого же предположения можно
получить и зависимость радиуса
обращения для серий Лаймана,
Бальмера, Пашека, Брекета и Пфунда
от частоты излучения.
Программа
позволяет использовать несколько
планов многофакторного
планирования (ортогональный,
рототабельный,
униформрототабельный и D
оптимальный Бокса) для четырех
факторов. Все они позволяют после
проведения экспериментов
обработать экспериментальные
данные и получить уравнение
регрессии, т.е. аппроксимировать
эти данные уравнением
Y = b0 + b1 * x1 + b2 * x2 + b3 * x3 + b4 * x4
+ b5 * x1 * x2 + b6 * x1 * x3 + b7 * x1 * x4 + b8 * x2 * x3 + b9
* x2 * x4 + b10 * x3 * x4
+ b11 * x1 ^ 2 + b12 * x2 ^ 2 + b13 * x3 ^ 2 + b14 * x4 ^ 2
где x1...x4 -факторы (параметры),
которые мы задаем при проведении
натурных или вычислительных
экспериментов в закодированном
виде
b0...b14 -коэффициенты которые у нас
получаются после обработки
результатов экспериментов по
определенной методике с
использованием метода наименьших
квадратов.
В программе
предусмотрено проведение трех
простейших вычислительных
экспериментов в которых
вычисляется критерий оптимизации Y(u)
и включив соответствующий
переключатель Вы можете выбрать
тестовый вариант, т.е. для проверки
программы <Y(u)=k1+k2*k3+k4^2>, вариант
демонстрации возможностей
статистики по нахождению
закономерностей в полном хаосе <Y(u)=u>
и вариант для которого собственно
программа и создавалась для
подбора коэффициентов в аналог
формулы Планка <Y(u)=k1*v^k2/exp(k3*v/k4)> (если
включен переключатель <с-1 в
знаменателе>, то в знаменателе
формулы добавляется минус еденица
и мы получаем формулу Планка).
Программа также позволяет
загрузить на обработку данные из
файла, если Вы проводили в
соответствии с планом натурные
эксперименты, и затем их результаты
занесли с помощью стандартной
программы <Блокнот> в файл Plank_plan(номер).dat
(программа позволяет загрузить из
файла и данные для построения
графика распределения по имеющимся
у Вас экспериментальным данным или
записать в файл данные
рассмотренного Вами распределения).
Особенностью оптимизации коэффициентов для формулы Планка будет то что значение критерия оптимизации будет не Y(u) и даже не как интеграл от этого выражения взятый по всему диапазону частот (выводится в окошке <E(rv(i)*dv(i))>), т.е. интегральная мощность излучения, а в процентах ошибки, т.е. как разность этой мощности излучения и мощности посчитанной по формуле Стефана-Больцмана (выводится в окошке <sigma*T^4>), деленная на последнюю и умноженная на 100. Значение интеграла определяется численными методами и количество элементарных интервалов dv задается в окошке <iMax>. И после получения уравнения регрессии на левом (маленьком) экране Вы увидите изменение критерия оптимизации в функции от одного из выбранных вами факторов, а на правом экране Вы увидите значения критерия оптимизации для всех экспериментов расчитанные по полученному уравнению регрессии и коэффициенты b0...b14 для него.
исполняемый файл Kniga2exe.zip - (Windows 95-98-XP-Vista-7,
46 kb)
исходные
файлы Kniga2vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 30
kb)
_____Данная программа является усовершенствованной версией программы Kniga1, в которой я добавил движение книги по оси Z, т.е. в направление перпендикулярном движению листа, который движется по оси X, и упростил определение среднего по пути движения коэффициента трения (причем теперь раздельно по двум осям), т.к. теперь средняя сила трения выводится уже в окончательном виде. Добавлены также еще один режим изменения скорости листа и вывод на осциллограмму скорости и координаты листа и сделаны некоторые мелкие усовершенствования.
Kniga1 - моделирование процесса выдергивания листа из под книги при различных режимах сухого трения в трущихся поверхностях.
исполняемый файл Kniga1exe.zip - (Windows 95-98-XP-Vista-7,
41 kb)
исходные
файлы Kniga1vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 27
kb)
_____Данная
программа моделирует процессы,
происходящие в простейшей системе,
состоящей из книги лежащей на листе,
который в свою очередь лежит на
столе, при движение листа с
различными режимами изменения
скорости, но ввиду того, что в ней
очень подробно описаны различные
режимы сухого трения, позволяет
воспроизвести очень сложные
процессы, которые возникают при
этом, и фокус, с выдергиванием
скатерти из под бутылки и фужеров,
является самым простым, что может
объяснить данная модель. А сама
идея, написать такую программу,
возникла после того, как на форуме
http://physics.nad.ru/rusboard/messages/49237.html был
задан (казалость бы элементарный
вопрос) - какая шайба при движение
по льду с одинаковой начальной
скоростью улетит дальше - та,
которая не будет при этом вращаться,
или, та, которая будет вращаться. И,
т. к. ответ на этот вопрос оказался
не таким простым и вызвал бурные
споры о сухом трение, я решил
написать эту программу, которая
позволяет ответить на многие
вопросы, которые возникли в ходе
обсуждения, а также могут
возникнуть в будущем.
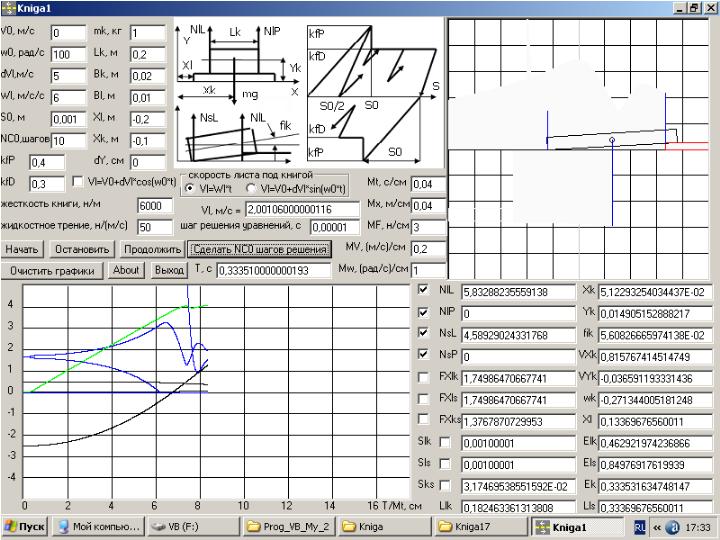
Konma2.0 - моделирование движения тел по окружности и вращательного
исполняемый файл Konma2exe.zip - (Windows 95-98-XP-Vista-7, 40 kb)
_____Эта программа позволяет смоделировать различные случаи вращательного движения груза прикрепленного к нити, которая может вращаться, как по конической поверхности, так и в горизонтальной плоскости. Нить пропущена в отверстие втулки, как это показано на рисунке, и может во время движения груза или медленно подтягиваться или отпускаться с заданной скоростью. При этом мы можем исследовать движение груза не только как материальной точки, но и как материального тела имеющего момент инерции относительно своего центра тяжести, а конкретно двух грузов закрепленных на концах жесткого стержня. Возможен вариант движения, когда во время движения груз массой 2 кг разделяется на две части, одна из которых остается прикрепленной к нити, а вторая продолжает движение по инерции до времени Tr (которое задается до эксперимента), а затем конец нити скользящий внутри второго груза стопорится и мы получаем систему из двух масс и двух нитей. Возможен вариант и когда весь груз 1 секунду движется по инерции, а затем конец нити стопорится во втулке (как раз этот эксперимент изображен на рисунке), а также комбинации этих вариантов и медленное вертикальное движение не только нити со скоростью VL, но и подвижной втулки внутри направляющей втулки с этой скоростью.
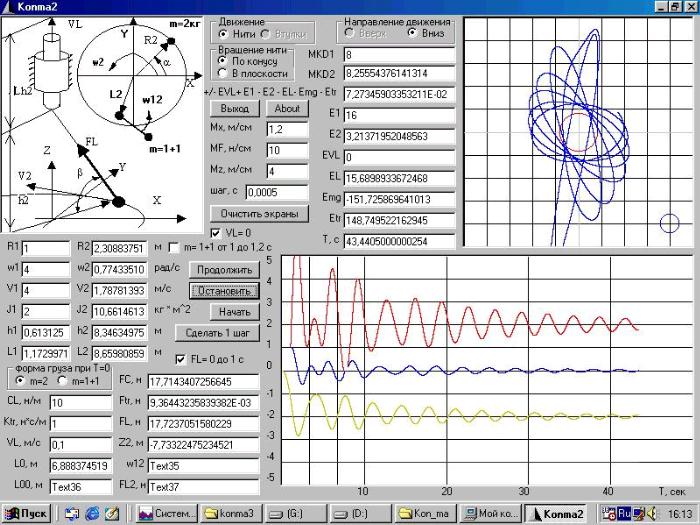
____Данная программа позволяет глубже понять основные законы механики и в частности первый закон Ньютона для вращательного движения, который в учебниках именуется законом сохранения кинетического момента. Во время работы программы на графики и в числовом формате выводятся не только координаты и скорости грузов, усилия возникающие в нитях и т.д., но и различные энергетические показатели работы системы такие как кинетическая энергия грузов, потенциальная энергия нити, энергия рассеянная в нити и т.д. Как и в программе Udar2 мы можем изменять шаг решения дифференциальных уравнений, описывающих движение груза, добиваясь необходимой нам точности проведения вычислительного эксперимента. Нажав кнопку <About> вы можете ознакомится с возможностями и работой программы более подробно.
QBasic (Оболочка языка QBasic, 286kb) - первые мои программы написаны для операционной среды DOS по этому, когда я даю такие программы как примеры для их просмотра и редактирования потребуется оболочка языка QBasic, которую сейчас уже трудно найти. По этому я решил выложить и ее. Правда, разрешения у Microsoft я на это не спрашивал, но я не думаю, что сейчас эта оболочка продолжает распространяться по лицензии также как, например, и одни из первых версий языка BasicM или Basic+, о которых многие даже и не слышали, а я все свои старые программы с этих языков переделал под QBasic.
Risunok5.0 - многооконный графический редактор с функцией мультикопирования
исполняемый файл Risunok5exe.zip - (Windows 95-98-XP-Vista-7, 196 kb)
исходные файлы Risunok5vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 252 kb)
______Основное назначение редактора (для чего он и создавался первоначально) - это качественное изменение размеров изображений. Например, все рисунки на этой странице уменьшены на 10% с использованием функции мультикопирования (MCopy), чтобы их было удобно просматривать в окне браузера и чтобы немного уменьшить размеры файлов. Стандартные графические редакторы, например, Paint входящий в комплект поставки Windows при уменьшении размеров изображения просто выкидывают часть строк и в результате, если толщина отдельных линий составляет один пиксель, они могут просто исчезнуть. Это, например, текст или линии разметки и Вы в этом можете убедится уменьшив изображение снимка с экрана программы Udar22 (файл Test.jpg входит в комплект поставки) с помощью редактора Paint на 10% и сравнив его с изображением полученным с помощью функции MCopy. Но если Вы пользуетесь профессиональными (одноэкранными) графическими редакторами, например, Adobe Fotoshop 5.0, то используя билинейный или бикубический методы преобразования параметров пикселей, Вы можете получить то-же качество изображения, что и при использовании функции MCopy.
_____Во время работы над программой, я решил дополнить ее небольшим редактором, чтобы можно было сделать на рисунке необходимымые надписи, линии выноски, проставить на графиках точки и при необходимости отредактировать отдельные фрагменты изображения. В результате получился очень функциональный редактор, который может не только проставить отдельный пиксель в точку с нужными координатами, но и цвет линий в нем можно задавать как с помощью стандартной палитры Windows, так и брать прямо с изображения и многое другое (корректировка цветов, реверс изображения, работа сразу в трех окнах, старение изображения и т.д.). Некоторое представление о его возможностях можно получить по этому дружескому шаржу на двух президентов (я думаю они на меня не обидятся).
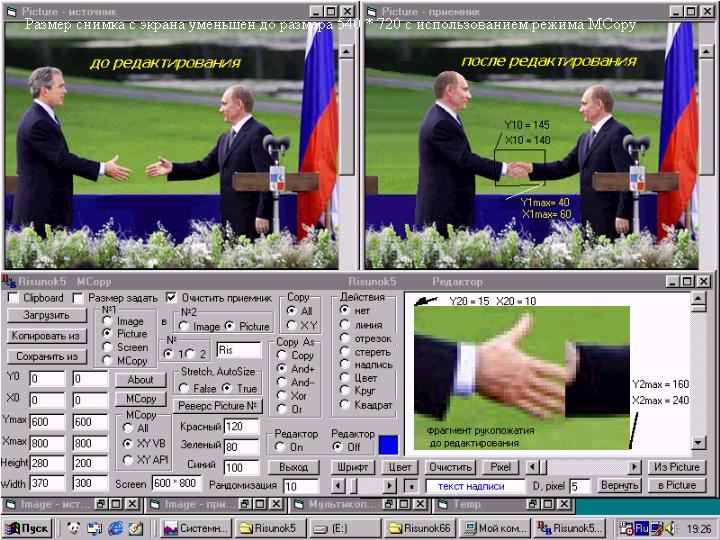
_______А после того как я дополнил редактор демонстрацией возможностей графических элементов Image и Picture, а также возможностей метода PaintPicture получилось очень приличное учебное пособие по работе с графикой языка VisualBasic6.0. Кроме этого данная программа будет полезна и по изучению методов чтения и записи данных, как в файл так и в буфер обмена. Но самое интересное - это реализация метода мультикопирования, как с использованием только возможностей VisualBasic6.0, так и с использованием функций API. Для начинающих программистов изучение варианта с использованием функций API, хотя оба варианта работают по одному алгоритму, очень затруднительно и я бы его не включал в программу, но он работает значительно быстрее, что очень заметно на изображениях превышающих размер экрана. Более подробно ознакомится с работой редактора Вы сможете нажав кнопку About в программе и прочитав коментарии в исходниках.
Grafik4 - построение новых и редактирование существующих графиков.
исполняемый файл, исходные файлы и прочие файлы Grafik4.rar - (Windows 95-98-XP-Vista-7, 149 kb)
Grafik3 - построение новых и редактирование существующих графиков.
исполняемый файл и прочие файлы Grafik3exe.zip - (Windows 95-98-XP-Vista-7, 131 kb)
исходные файлы Grafik3vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 156 kb)
_____Даннаяа программа отличается от первой версии тем, что теперь появилась возможность наложить один график (рисунок) на другой и потм сохранить уже комбинированное изображение. Появилась также возможность не вручную подбирать коэффициенты для аналитической кривой аппроксимирующей загруженные из файла данные, а делать это программно с использованием метода наименьших квадратов. Правда из трех аналитических кривых теперь осталась только одна - квадратичная аппроксимация, но она является самой распространеной. Добавлена также возможность читать спецефические данные созданные программой Solsys, где дата наблюдения задается юлианской датой, а программа переводит ее в год наблюдения с дробной частью.
Grafik1 - построение новых и редактирование существующих графиков.
исполняемый файл и прочие файлы Grafik1exe.zip - (Windows 95-98-XP-Vista-7, 60 kb)
исходные файлы Grafik1vbp.zip - (Windows 95-98-XP-Vista-7, Visual Basic 6.0, 22 kb)
_____Хотя данная
программа и базируется на коде
программы Risunok5, но является
принципиально другой программой. А
основным ее отличием является
возможность наносить на рисунок
точки в заданном масштабе, т.е.
строить графики. Причем график
можно построить и как
аналитическую кривую, задав
значения коэффициентов для
нескольких типовых зависимостей, и
по отдельным точкам, задавая каждый
раз значение аргумента и значение
функции. А можно нанести точки и из
файла данных, где данные должны
быть записаны в определенном
формате, т.е. в том формате, в
котором данные записываются при
работе программ, например, Solsys или
ObsData. При этом можно как создать
новый график, так и
откорректировать уже существующий,
загрузив его из файла в формате bmp,
gif, jpg или ico.
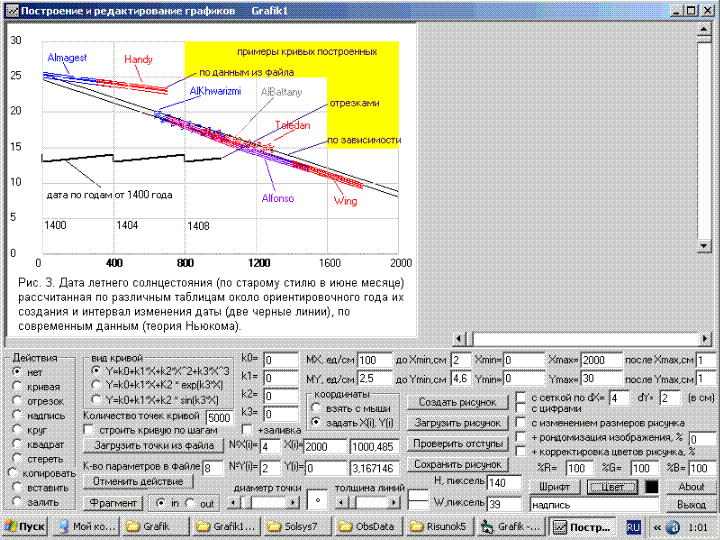
Если Вы будете
редактировать уже существующий
график, Вы можете изменить размер
рисунка, чтобы работать с рисунком
в заданном Вами масштабе. При этом
Вы можете также подкорректировать
цвета на этом рисунке и немного как
бы состарить рисунок. На созданном
Вами чистом графике или уже
существующем Вы можете рисовать
точки (круг или квадрат) и линии,
вставлять надписи и фрагменты
изображения, а также стирать белым
цветом круг или заливать
произвольным цветом выделенный
фрагмент рисунка. При этом,
внутреннюю область точки можно
заливать тем же цветом, что она
нарисована, а фрагмент рисунка
можно не только вставлять на наш
график, но и копировать любой
фрагмент графика в буфер обмена. И,
как я уже писал, можно несколькими
способами нанести на график кривую.
Для всех этих действий координаты
Вы можете задавать двумя способами
- или задавая координаты с мыши или
задавая их в окошках в масштабе
графика.
При этом, Вы можете задать
произвольный размер точки на
графике, толщину линии, шрифт и его
размер, а также задать для них
произвольный цвет. А, если Вы
совершили какое-то ошибочное
действие, то Вы можете отменить это
действие и Вы восстановите прежнее
изображение. После создания
графика, Вы можете его сохранить (только
в формате bmp). Для более подробного
описания программы надо нажать на
форме программы кнопку <About> или
прочитать файл Grafik1.doc.
Spusk -моделирование движения тела по направляющей в поле постоянной напряженности.
Архив
программ TestSpusk.rar - (DOS, Windows
95-98-XP-Vista-7, 411 kb)
Архив
программ TestSpuskM2.rar - (DOS, Windows
95-98-XP-Vista-7, 401 kb)
____Коллекция программ Spusk, написана
на разных языках программирования C++,
Turbo Pascal, Visual Basic 6.0, Visual Basic NET, Free Basic и
еще нескольких языках Basic под DOS, и
все они решают одну задачу –
моделируют движение тела по
различным направляющим в поле
постоянной напряженности. За
основу алгоритма работы всех
программ я взял алгоритм
примененный Kostya в программе code.cpp,
распечатку которой он выложил на
сайте http://physics.nad.ru/aniboard/messages/291.html , и постарался
максимально сохранить обозначения
примененные Kostya, но сам алгоритм
программирования в разных
программах немного отличается с
учетом специфики того или иного
языка. Все эти программы были
использованы мною при написание
статьи “Выбор языка
программирования для научных
работников” (см. в разделе статьи),
где в результате сравнения
различных языков по нескольким
критериям был сделан выбор в пользу
языка программирования Visual Basic 6.0.
По мере написания программ в первом
варианте я их сразу выкладывал
здесь для скачивания, а сегодня я
выкладываю исходники и
откомпилированные файлы этих
программ в одном архиве TestSpusk.rar.
Во время работы над статьей я значительно модифицировал эти программы, чтобы во-первых сблизить их по функциональным возможностям при сравнительных испытаниях, а во-вторых, чтобы опробовать на них различные методы позволяющие повысить эффективность их работы. Например, в программе SpuskVB6MM я опробовал несколько различных режимов организации циклов вычислений с выводом изображения на экран после выполнения заданного количества шагов решения и это мне позволило, организовав циклы вычислений не по таймеру Visual Basic 6.0, как это обычно делалось, повысить быстродействие программы на порядок. А исключение визуальных элементов из критичного кода, т.е. выполняемого многократно циклами, в программе SpuskVB6MV позволило повысить быстродействие программы еще до 3-х раз на некоторых режимах. Вынос же всего критичного кода в библиотеку DLL, написанную на Free Basic, в программе SpuskVB6MVdllFB позволило в сумме получить скорость работы программы на некоторых режимах даже выше чем в программе SpuskSiM, написанной на чистом С++. Все эти и написанные на других языках программирования модернизированные программы я поместил в архив TestSpuskM2.rar, а здесь удаляю все выложенные ранее коды программ и их скриншоты и оставляю для примера только внешний вид (скриншот) программы SpuskVBnet, написанной на языке Visual Basic с применением технологии NET.