МЕХАНИКА ДЛЯ КВАНТОВОЙ МЕХАНИКИ

                                                             Часть 6. Эффект Доплера

                                  .третья редакция (переработанная и дополненная) 08.08.2015                                                                                  

                                                .вторая редакция (дополненная) 25.04.2014                                                                                 

                                                            первая редакция 13.04.2014      

С. Ю. Юдин          http://modsys.narod.ru  .                                                                     . modsys@yandex.ru

                               https://googledrive.com/host/0BwnV2Ac6zvhMalpOVGktQ1Jic1U

 

 

Введение

1. - Обзор основных формул по эффекту Доплера.                                                                                     1

2. - Экспериментальное подтверждение формул по эффекту Доплера для света.                                  13

3. - Проверка различных формул для общего эффекта Доплера при проведении вычислительных

экспериментов на математической модели этого эффекта.                                                                       45

Выводы                                                                                                                                                            52

Список литературы                                                                                                                                         52

Приложение 1. Анализ классических формул Замятина и Акимова дающих поперечный эффект

Доплера.                                                                                                                                                           55

Приложение 2. Отличие моделей от имитаторов и натурного эксперимента от вычислительного.      66

 

 

 

 

                                                                        Введение.

 

В данной статье я рассматриваю различные как классические так релятивистские формулы для эффекта Доплера, как в чисто теоретическом плане, так и их экспериментальную проверку. Что касается классических формул, то здесь и теоретически и экспериментально подтверждается формула Лоренца, но со сделанными мною небольшими поправками, а именно по уточнению углов с учетом запаздывания сигнала при его распространения в пространстве от источника до приемника и двух аберрационных поправок, которые возникают в самих источнике и приемнике. Поэтому все современные классические формулы, например, Замятина или Акимова, дающие поперечный эффект Доплера, являются ошибочными, а поперечный эффект в них появляется из-за ошибок при выводе формулы. Точно так же и различные релятивистские формулы (Эйнштейна, Ландау и Айвса), в которых краеугольным камнем является именно поперечный эффект Доплера, тоже являются ошибочными, т.к. не подтверждаются экспериментально при грамотном выполнении экспериментов. При этом даже, если бы релятивистские формулы для эффекта Доплера и подтверждались экспериментально, они никоим образом не доказывали бы вывод СТО о замедлении темпа течения времени на движущихся объектах, т.к. релятивистский множитель в них не имеет к этому никакого отношения. А сами формулы при немного разных условиях дают или эффект замедления времени или эффект ускорения и как частный случай полное отсутствие эффекта Доплера. Т.е. непосредственно к эффекту Доплера все эти релятивистские формулы имеют очень отдаленное отношение, хотя иногда и создают иллюзию чего-то похожего. К тому же, все релятивистские формулы при одних и тех же условиях дают разные результаты для общего эффекта Доплера, что указывает на теоретическую неоднозначность СТО, с использованием которой и получены все эти формулы.  

 

 

 

                                       1. Обзор основных формул по эффекту Доплера

 

Вы удивитесь, но для такого вроде бы элементарного физического явления, как эффект Доплера в общем виде, а не для частного случая продольного эффекта, который рассмотрел сам Доплер, известно более десяти формул (Лоренца, Эйнштейна, Шредингера, Блохинцева, Замятина и другие). И это при том, что в большинстве случаев мы сами создаем передаваемый сигнал и сами же его фиксируем. Поэтому, я надеюсь, Вы понимаете насколько сложно описать те явления, где мы являемся только сторонними наблюдателями, как, например, с гравитацией, где мы примерно так же, как и Аристотель, можем только наблюдать, что тяжелые предметы падают быстрее, чем легкие, и делать из этого свои выводы. Вот поэтому у меня и возникает столько проблем в цикле статей "Скорость гравитации", где я пытаюсь только по данным пассивных наблюдений за планетами Солнечной системы или наблюдений за двойными пульсарами определить скорость гравитации. А пишу я сейчас о гравитации по той простой причине, что именно при рассмотрении гравитационного взаимодействия двух тел у меня получилась формула (1) подобная формуле (3) для эффекта Доплера и в связи с этим я и занялся подробным изучением этого эффекта, чтобы прояснить для себя некоторые моменты в своей формуле (1). Да и сама эта статья является переработанным приложением 2 к первой и второй редакциям статьи "Влияние скорости гравитации на смещения параметров орбит планет" [10], которая в свою очередь является 4-ой частью цикла статей "Скорость гравитации". 

 

Но и сам по себе эффект Доплера даже в классическом виде оказался очень запутанным физическим явлением поэтому и сейчас в Интернете идет активное обсуждение этого вопроса, где наиболее заметными участниками являются Акимов и Купряев. Первый отстаивает свою формулу (упрощенная формула Замятина), а второй пытается доказать справедливость формулы Лоренца. В связи с этим я в приложении 1 рассмотрю и их работы, но большую часть статьи займет разбор различных релятивистских формул. А результатом моего изучения вопроса по эффекту Доплера стало то, что я предложил еще одну формулу для этого эффекта (3), которая с аберрационными поправками будет выглядеть как (3-2), которую, как и все мои предшественники, я, конечно же, считаю единственно правильной. А самая известная из всех формул это формула Лоренца (2), хотя быстрее всего автор этой формулы не известен, но ее называют именем Лоренца для определенности.

 

 

При этом напоминаю, что все формулы для классического эффекта Доплера подразумевают наличие среды, в которой распространяются с заданной скоростью сигналы от источника к приемнику, и поэтому скорости источника и приемника используются заданными относительно этой среды, а в релятивистских формулах бывает по разному, но в самой первой формуле у Эйнштейна среда отсутствует, а скорость используется относительная, т.е. скорость приемника относительно источника. При этом, обращаю Ваше внимание, что правильно понять смысл, заложенный во всех этих формулах, можно только уяснив себе, что все они являются просто имитаторами (симуляторами) этого эффекта. Поэтому, желательно, перед началом чтения ознакомиться с приложением 2, чтобы понять, что имитатор это не аналитическое описание какого-то явления (этим занимается модель явления), а это только описание результата функционирования системы воспроизводящей этот эффект.

 

 

Давайте рассмотрим некоторые нижеприведенные формулы, где v0 - исходная частота передатчика на движущемся источнике сигнала, т.е. в его системе отсчета, а v - частота сигнала, который распространялся в какой то среде или в вакууме со скоростью Vs и был принят на движущемся приемнике в его системе отсчета. При этом b1=V1/Vs и b2=V2/Vs, где V1 это скорость приемника сигнала и V2 это скорость источника сигнала, а Q1 и Q2 это углы между этими скоростями и радиус-вектором, соединяющим источник 2 и приемник 1 в текущий момент времени. Во всех приведенных формулах у меня положительной считается скорость в направлении распространения сигнала от источника к приемнику, где расположен наблюдатель, т.е. в направлении обратном общепринятому понятию луча зрения, когда говорят о лучевых скоростях и когда положительным направлением считается направление от наблюдателя на источник сигнала. Формула Лоренца (2) в принципе правильно отражает сам эффект Доплера, но с некоторой погрешностью. А если в этой формуле учесть запаздывание по координатам, о котором я писал в [10], и аберрационные поправки, о которых я расскажу позже, чтобы сейчас не усложнять анализ, то этой погрешности не будет. Таким образом, надо  вместо углов Q1 и Q2 в формуле (2) использовать углы A1 и A2 между векторами скорости приемника и источника и радиус-вектором распространения сигнала из той точки 2', где был источник, когда сигнал его покинул, в точку 1, где его принял приемник и получим формулу (3).

 

 

F(i,k) = Fn(i,k)*(1 – Vk/Vgr) / (1 – Vi/Vgr)                      (1)

 

v =v0*(1 – b1*cos(Q1)) / (1 – b2*cos(Q2))                       (2)

 

v =v0*(1 – b1*cos(A1)) / (1 – b2*cos(A2))                        (3)

 

v =v0*(1 – b*cos(Q12)) / sqrt(1 – b^2)                                   (4-1)

 

v =v0*sqrt(1 – b^2) / (1 – b*cos(Q12))                                  (4-2)

 

v =v0*sqrt(1 – b^2) / (1 + b*cos(Q12))                                  (4-3)

 

v =v0*(1 – b*cos(Q12))                                                           (4-4)

 

 

 

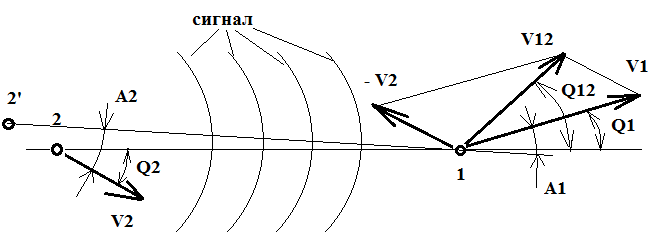
Рис. 1. Схема для расчета эффект Доплера в общем виде.

 

Но для эффекта Доплера существует еще и релятивистская формула Эйнштейна (4-1), которую он предложил в работе [8], и которая, естественно, принципиально отличается от классических формул.  Ведь согласно теории относительности не может быть абсолютных скоростей, а есть только относительные скорости (хотя это было ясно еще и Ньютону), и поэтому, если формулу (4-1) рассмотреть в упрощенном виде, как формулу (4-4), то в ней будет присутствовать только коэффициент b. Он равен скорости приемника относительно источника V12= V1-V2 деленной на скорость распространения сигнала Vs, которая в этой релятивистской формуле, равна скорости света "с". К тому же релятивистскую формулу рекомендовано применять только для световых волн в вакууме, где отсутствует система отсчета, связанная со средой, в которой распространяется волна, но все ее применяют где им вздумается.

 

 

Если использовать только числитель формулы (4-1), т.е. формулу (4-4), то получающийся результат будет при малых скоростях незначительно отличаться оттого, что дает формула Лоренца, а при неподвижном источнике результат будет вообще полностью совпадать. Естественно, эта формула будет давать и ту же ошибку, что и формула (2), т.к. угол Q12 это угол между вектором скорости приемника относительно источника и радиус-вектором соединяющим источник и приемник в текущий момент времени, и, следовательно, этот угол тоже не учитывает запаздывание по координатам. Но здесь еще появился дополнительный релятивистский множитель, который дает, так называемый, поперечный эффект Доплера, которого нет в классической формуле (2). Однако, некоторые альтернативные ученые пытаются доказать, что такой эффект существует и в их классических формулах для эффекта Доплера. Я же в их формулах (см. приложение 1) кроме ошибок никакого поперечного эффекта Доплера не нашел. А откуда же он тогда взялся в формуле (4-1), т.е. чем она еще отличается от классической (2).

 

 

До написания этой статьи лично у меня сложилось такое впечатление, что формула для релятивистского эффекта Доплера существует в единственном числе и отличается от классической только использованием относительной скорости и релятивистским множителем, а при малых скоростях она переходит в классическую формулу эффекта Доплера (2). А, объясняя наличие поперечного эффекта Доплера, которого принципиально нет в классическом варианте, говорят, что релятивистская формула учитывает, согласно СТО, замедление времени в движущихся системах. Причем, оно замедляется и при движении источника вдоль линии соединяющей источник и приемник (продольный эффект Доплера) и при движении в поперечном направлении (поперечный эффект Доплера). В результате, например, при движении звезд относительно Земли спектр их излучения смещается в красную сторону, как при их удалении, так и при движении с постоянным расстоянием до них. Я думаю, что у Вас сложится точно такое же впечатление, если Вы прочитаете, например, учебник [19] (см. сканы, но учтите, что здесь другая индексация у источника и приемника и при этом положительное направление их скоростей принято в другую сторону, а V (у меня V12) вычисляется также, как V1-V2). В этом описании все выглядит очень безобидно и даже как-то тривиально, поэтому и не возникает желания вникать более глубоко в смысл релятивистской формулы, но давайте все же попробуем это сделать.

 

 

 

И так, начнем с того, что, как правильно заметил автор работы [5], формула (4-1) дает, например, при поперечном эффекте Доплера не замедление времени на источнике сигнала, а убыстрение, т.к. частота принимаемого сигнала увеличивается. Таким образом, формула (4-1) дает нам в этом случае фиолетовое смещение в спектре звезд. Начинаем разбираться и видим, что авторы учебников, когда речь идет о замедлении времени на источнике сигнала для получения поперечного эффекта Доплера, используют формулу (4-2), которая действительно дает замедление времени на источнике сигнала. А иногда, как в  приведенных выше сканах, встречается и формула (4-3), которая отличается от (4-2) только знаком у скорости, но это опять таки не формула Эйнштейна. А автор [24], даже явно указывая на Эйнштейна, тоже, почему-то, приводит формулу (4-2).

 

 

 

А автор учебника [11] ухитрился на странице 469 (см. скан) привести и формулу (4-1), которая находится у него чуть выше формулы (151.4), а на следующей странице 470 приводит формулу (151.8), т.е. формулу (4-2), но урезанную до поперечного эффекта Доплера. Но формулы то эти совершенно разные и в одном случае будет замедление времени на источнике сигнала, а в другом ускорение. И видимо, чтобы такое противоречие было не очень заметно, он в одном случае приводит формулу для общего эффекта Доплера, а в другом только для поперечного и при этом еще и делает замену обозначений, но вопросов от этого не становится меньше, т.к. автор совершенно не делает никаких пояснений по применению то одной, то другой формулы.

 

 

 

Вот и в работе [6] на стр. 124, когда речь идет о замедлении времени на источнике сигнала для получения поперечного эффекта Доплера, мы опять видим урезанную до поперечного эффекта Доплера формулу (4-2), но ведь Эйнштейн ясно написал для своей формулы (4-1), что "Это и есть принцип Доплера для любых скоростей", т.е. других релятивистских формул вроде бы быть не должно, т.к. он ничего не уточнял по поводу ее применения. Правда, при выводе своей формулы Эйнштейн рассматривал частный случай, когда источник покоится, а приемник движется. Таким образом, если в СТО время замедляется на движущихся объектах, то в этом случае у него время должно было замедляться на приемнике, а не на источнике и логично она бы выглядела только для частного случая, т.е. при движении приемника. А вот формула (4-2) логично с точки зрения СТО выглядела бы для частного случая, когда движется источник сигнала. Оказывается, так оно и есть, и мы видим у Ландау [20] вывод формулы (4-2) именно для этого частного случая. Кто первый получил эту формулу я не знаю, поэтому буду для определенности называть ее иногда формулой Ландау.

 

 

Да, теперь логически все сходится, но получается, чтобы не было парадоксов с эффектом замедления времени на движущихся объектах, формулы (4-2) или (4-3) надо применять в том случае, когда покоится приемник, а формулу (4-1) надо применять, когда покоится передатчик. Позвольте, но в чем же тогда тут относительность, если для СТО требуется абсолютная система отсчета (АСО), а не инерциальная система отсчета (ИСО). Таким образом, получается, что для релятивистского эффекта Доплера не все системы отсчета равноправны, т.к. нам надо знать, что покоится в АСО - источник или приемник, чтобы узнать какой формулой пользоваться. Но такой выбор ИСО коренным образом противоречит СТО, где события протекают одинаково во всех инерциальных системах и, следовательно, должны описываться одной формулой независимо от выбора ИСО приемника или ИСО источника. Естественно, этого противоречия не могли не заметить и сторонники СТО, поэтому они решили подправить Эйнштейна и в последнее время очень многие из них предлогают формулу (4-5), которая отличается от классической (2) только наличием двух релятивистских множителей. Смотрите, например, здесь [22] или здесь [23].

 

v =v0*[1 – b1*cos(Q1)] / [1 – b2*cos(Q2)]                       (2)

 

v =v0*[(1 – b1*cos(Q1)) * sqrt(1 – b2^2)] / [(1 – b2*cos(Q2)) * sqrt(1 – b1^2)]                       (4-5)

 

 

Как уверяют авторы, эта формула полностью соответствует СТО и здесь углы и скорости V1 и V2 берутся в произвольной ИСО, где в данный момент находится наблюдатель. Это может быть и ИСО приемника и ИСО источника и любая другая ИСО. Вот только сути противоречия и эта формула не устраняет, т.к. здесь результат расчета будет зависеть от выбора ИСО, где будут заданы эти скорости. А при этом я совершенно не понимаю как наблюдатель находящийся не на приемнике может именно наблюдать эффект Доплера, который является физическим, а не кинематическим эффектом. Если мы наблюдаем за кинематическим эффектом, например, за перемещениями игроков и футбольного мяча по полю, то мы можем наблюдать это и находясь на трибунах стадиона и пролетая над стадионом на самолете, а вот с физическими эффектами так не получится. Например, я не понимаю, как наблюдатель, находящийся на Земле, может наблюдать силу гравитационного притяжения космонавта находящегося на Луне или тот же эффект Доплера при передаче сигнала со спутника на Луну.

 

 

На это мне сторонники СТО отвечают, что частота v0 измеряется наблюдателем, находящимся в ИСО источника, а частота v измеряется наблюдателем, находящимся в ИСО приемника, и только скорости и углы могут определяться в любой произвольной ИСО, т.е. даже третьим наблюдателем. Я считаю, что у нас тут многовато получилось наблюдателей, но раз они так нравятся сторонникам СТО, то закроем на это глаза, т.к. я тут вижу более серьезный недостаток этой формулы. Ведь здесь получается, что с использованием этой формулы мы можем определить абсолютную скорость нашей ИСО, в которой мы задаем скорости источника и приемника, а это прямое противоречие принципам СТО и ниже я приведу численный пример, который позволяет определить абсолютную скорость нашей ИСО.

 

 

К тому же, меня удивляет почему авторы современных работ по формуле (4-5) никто не упоминает Айвса, который получил эту формулу еще в 1937 году [16] исходя из эфирной концепции Лармора-Лоренца, а не исходя из СТО, т.к. был ярым противником СТО. Да, да это тот самый Айвс, который вместе с Стилуэллом в 1938 году и потом в 1941 году [17, 18] экспериментально и подтвердил справедливость своей формулы (4-5), но сейчас в учебниках его экспериментальные данные используют как подтверждение формул (4-1) и (4-2) потому, что Джинс дал им иное толкование. Что касается экспериментальной проверки этих формул, то на этом я остановлюсь ниже, а сейчас я бы хотел заметить, что Айвс тоже считал возможным, исходя из формулы (4-5), экспериментально определить абсолютное движение в эфире, что противоречит постулатам СТО, поэтому формула (4-5) никак не может соответствовать СТО как бы современным защитникам СТО этого не хотелось.

 

 

Ну и, прежде чем приступить к практической проверке различных формул для эффекта Доплера, хотелось бы остановиться на еще одном моменте. Поперечный эффект Доплера у нас получается из-за замедления времени, которое дает релятивистский множитель, но этот множитель используется и в расчетах поперечного эффекта Доплера и в расчетах продольного эффекта Доплера. Поэтому этот эффект замедления времени никак не является именно поперечным и здесь надо говорить о другом названии для этого эффекта. А по аналогии с гравитационным замедлением времени, которое дает ОТО, его можно назвать скоростным замедлением времени СТО, т.к. и там и там этот эффект уменьшения исходной частоты передатчика расположенного на источнике объясняется замедлением времени на источнике и эти эффекты не зависят от направления движения источника. А, т.к. последнее, т.е. именно разность скоростей вдоль линии, соединяющей источник и приемник, является краеугольным камнем эффекта Доплера, то и эффект от скоростного замедления времени не имеет прямого отношения именно к самому эффекту Доплера. И формула именно для эффекта Доплера, согласно требованиям СТО, должна бы выглядеть как (4-4), а эффект от замедления темпа течения времени должен был бы рассматриваться уже отдельно.

 

К тому же, как пишет автор [37] любая релятивистская формула может давать при некоторых сочетаниях скорости и угла или уменьшение частоты принимаемого сигнала или увеличение. А вот автор темы по эффекту Доплера на форуме dxdy [31] даже приводит по этому поводу очень наглядный пример В. Квитко. Если мы зададим b=0,8 и Q=60 градусов, то по формулам (4-1) и (4-3) у нас получится v=v0, т.е. нет никакого эффекта Доплера, но при дальнейшем увеличении скорости у нас по формуле (4-1) будет v>v0 и при уменьшении v<v0, а по формуле (4-3) наоборот, т.е. опять проснется эффект Доплера, но результаты будут коренным образом противоречить этому принципу. Таким образом, релятивистские формулы для эффекта Доплера вообще не имеют никакого отношения к этому эффекту, а некоторая схожесть результатов с классическим эффектом Доплера при рассмотрении продольного эффекта это только иллюзия аналогии с этим эффектом.

 

 

Ну а теперь давайте плавно перейдем к дальнейшему рассмотрению всех этих формул на численных примерах. На рис. 2 мы видим результаты вычислений по различным формулам для продольного эффекта Доплера при покоящемся источнике и движущимся приемнике, а на рис. 3 наоборот. При этом по оси X отложена скорость движущегося источника или приемника в долях скорости распространения сигнала, а по оси Y частота сигнала в долях исходной частоты (v/v0), которую мы фиксируем на приемнике сигналов. Причем, во всех примерах, чтобы избежать громоздких расчетов, я буду задавать условные скорости в м/с, и при этом приму Vs=20 м/с, а т.к. у нас во всех расчетах используются скорости в долях Vs, то это никак не отразиться на результатах, т.е. получится то же самое, как если бы мы использовали реальные скорости.

 

 

 

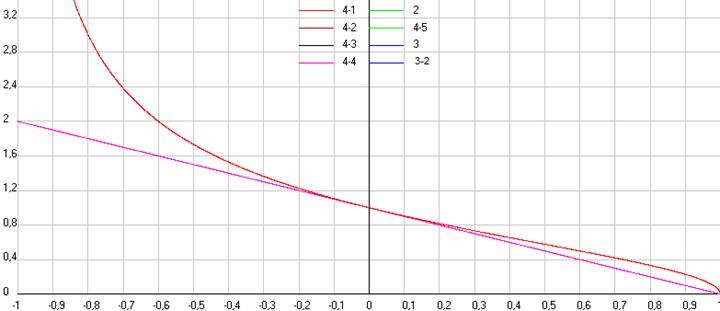
Рис. 2. Сравнение результатов расчетов по различным формулам при продольном эффекте Доплера, когда у нас покоится источник и движется приемник. Сиреневая линия по формулам 4-4, 2 и 3, а красная 4-1 или 2  как 4-5. Скриншот программы Dopler4.

 

 

Как мы видим на этом рисунке, здесь классические формулы (2) и (3), которые при продольном эффекте Доплера ничем не отличаются, дают тот же результат, что и упрощенная релятивистская формула (4-4), а вот при наличии в формуле (2) релятивистских множителей, т.е. использование ее как формулы (4-5),  она даст тот же результат, что и формула (4-1). Но вот, когда у нас движется источник, а покоится приемник (см. рис. 3), то здесь мы видим уже большее разнообразие получающихся результатов. Упрощенная релятивистская формула (4-4) дает такую же линейную зависимость, как и при движущемся приемнике, а классические формулы (2) и (3) дают уже нелинейный эффект так же, как и релятивистская формула  (4-3). Но, если мы будем использовать формулу (2) с релятивистскими множителями, т.е. как (4-5), то мы опять получим тот же результат, как и по релятивистской формуле (4-3).

 

 

Причем, что интересно отметить, чисто математически получается, что формулы (4-1) и (4-3) дают один и тот же результат для продольного эффекта при одинаковом значении V12. Таким образом, можно было бы снять замечания к релятивистскому эффекту Доплера по различию формул для двух частных случаев - движения источника или движения приемника, но такой вывод преждевременный. Как мы уже видели выше, эти формулы дают совершенно противоположные эффекты в случае поперечного эффекта Доплера и, следовательно, они дадут совершенно разные результаты и для общего эффекта Доплера.

 

 

 

 

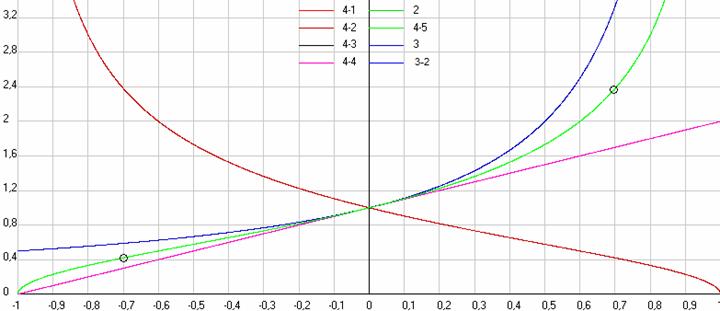
Рис. 3. Сравнение результатов расчетов по различным формулам при продольном эффекте Доплера, когда у нас покоится приемник и движется источник. Сиреневая линия 4-4, синяя 2 и 3, зеленая 4-3 или 2 как 4-5, и красная 4-2. Скриншот программы Dopler4.

 

 

А вот формула (4-2) получается у нас явно ошибочной, т.к. здесь не правильно задан знак у скорости приемника относительно источника, при том определении как я задал это значение V12=V1-V2, и, если учесть мое определение скорости V12, то правильной у нас получится формула (4-3). Хотя, можно с пользой использовать и формулу (4-2) в моих обозначениях, т.к. она, как не странно, дает при этом правильный график изменения принимаемой длины волны в долях исходной длины волны для обеих формул (4-1) и (4-3), т.е. если ее использовать или для движущегося приемника или для движущегося источника. Но в программе Dopler4, с использованием которой мы и производим все эти расчеты, она нам не пригодится, т.к. в программе есть чекбокс <L/L0>, включив который, мы можем произвести расчеты по всем вышеприведенным формулам для изменения длины волны, а не частоты принимаемого сигнала. Таким образом, при том определении как я задал значение V12=V1-V2, нам надо вместо формулы (4-2) использовать (4-3), но чаще всего в различных расчетах многие авторы используют именно формулу (4-2), поэтому, когда я буду разбирать применение этой формулы у них, то мы будем иметь ввиду, что у этих авторов скорость имеет обратный знак, т.е. при положительной скорости источника V2 он приближается к приемнику, но относительная скорость V12 берется положительная.

 

 

Как видим, и в общем эффекте Доплера (см. рис.4) при движении приемника под разными углами вектора его скорости к радиус-вектору у нас будет не большое разнообразие результатов. Упрощенная релятивистская формула (4-4), т.е. именно для эффекта Доплера, дает те же результаты, что и формулы (2) и (3), где в расчете V12/Vs = VX1/Vs = 14/20 (VX2=0, VY1=0, VY2=0, Y1=50 м, Y2=0 м), а формула (4-1) даст тот же результат как (2) в варианте (4-5).

 

 

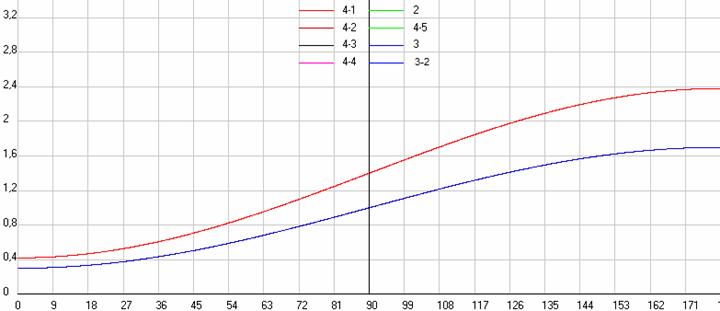
Рис. 4. Сравнение результатов расчетов по различным формулам для общего эффекта Доплера при изменении углов Q1 и Q12 (источник неподвижен, а горизонтально движется приемник на высоте 50 м). Синяя кривая 2, 3, 4-4, а красная 4-1 или 2 как 4-5. Скриншот программы Dopler4.

 

А вот при неподвижном приемнике и движении источника V12/Vs = -VX2/Vs = -14/20 (VX1=0, VY1=0, VY2=0) результаты будут уже более разнообразные (см. рис. 5). Формула (4-4) дает просто зеркальное отражение того, что было на рис. 4, а формула (4-3) хоть и дает зеркальное отражение, но только в самых концах графика, т.е. при продольном эффекте. А вот формулы (2) и (3) дадут существенно другие результаты как по соотношению частот на концах графиков, так и по форме кривых.

 

 

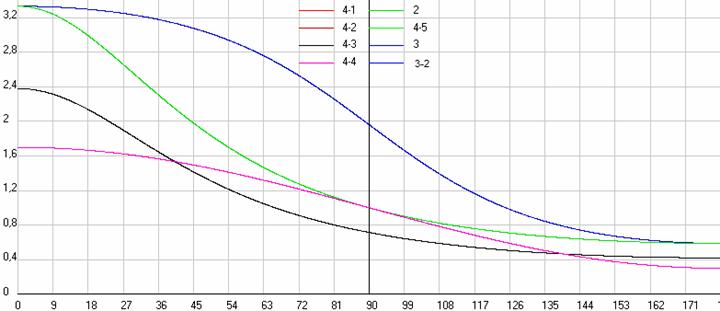
Рис. 5. Сравнение результатов расчетов по различным формулам для общего эффекта Доплера при изменении углов Q1 и Q12 (источник движется параллельно горизонту, а приемник покоится на высоте 50 м). Сиреневая кривая 4-4, зеленая 2, синяя 3, а черная 4-3 и 2 как 4-5. Скриншот программы Dopler4.

 

А теперь давайте проверим наше с Айвсом утверждение, что формула (4-5) позволяет определить абсолютную скорость нашей системы. Допустим, что абсолютная скорость нашей ИСО равна 4 м/с и в ней движутся в том же направлении с абсолютными скоростями - источник V2=12 м/с и приемник V1=16 м/с. Таким образом, скорость приемника относительно источника V12= 4 м/с и формулы (4-1) и (4-3) нам при продольном эффекте Доплера дадут результат v=v0*0,816. Теперь, пусть мы с Вами знаем этот результат из эксперимента и нам известна в нашей ИСО скорость приемника 12 м/с и источника 8 м/с. Для того, чтобы нам найти абсолютную скорость нашей ИСО, мы задаемся различными скоростями нашей ИСО, т.е. Vисо, в АСО и вычисляем какие при этом будут скорости приемника V1 и источника V2, а затем рассчитываем по формуле (4-5) получающийся результат для наблюдателя находящегося на приемнике.

 

Vисо = 8    V1=4     V2=0       v=v0*0,816

Vисо = 4    V1=8     V2=4       v=v0*0,802

Vисо = 0    V1=12   V2=8       v=v0*0,763

Vисо = -4   V1=16   V2=12     v=v0*0,666

 

Следовательно, получается, что наша ИСО движется относительно АСО со скоростью 8 м/с. Таким образом, формула (4-5) противоречит принципам СТО, т.к. позволяет по результатам эксперимента найти абсолютную скорость системы. К тому же, здесь получился такой конфуз, что у нас по формуле (4-5) получилась скорость системы 8 м/с, а по формулам (4-1) и (4-3) такой результат должен был быть при Vисо= 4 м/с. Следовательно, формула (4-5) и по результату не согласуется с формулами (4-1) и (4-3), но, как мы увидим далее, ее все равно используют при обосновании поперечного эффекта Доплера именно как формулу соответствующую всем принципам СТО.  

 

 

  

2. - Экспериментальное подтверждение формул по эффекту Доплера для света.

 

В общем-то, экспериментальной проверки для света различных формул общего эффекта Доплера почти никогда не проводилось, если не считать экспериментов [21], хотя это можно сделать и на установке [7,25]. Во всех экспериментах, которые проводились, преследовалась цель экспериментально подтвердить эффект замедления времени, который дает поперечный эффект Доплера, но все первые эксперименты выполнялись именно при наблюдении продольного эффекта Доплера. При этом, для доказательства справедливости релятивистской формулы эффекта Доплера, использовался такой показатель, как смещение средней длины волны dL=L0*b^2/2 от ее исходного значения. Здесь среднее значение экспериментально определяется как полусумма двух смещений полученных при одинаковой скорости источника и одном угле наблюдения, но при движениях в разных направлениях или при наблюдении движения в одном направлении с одинаковой скоростью под двумя разными углами (0 и 180 градусов). При этом принимается, что релятивистская формула принципиально отличается от классической только наличием релятивистского множителя, дающего эффект замедления времени на движущемся источнике или приемнике сигнала, который и приводит к поперечному эффекту Доплера. Ведь при отсутствие этого множителя, например, при движении приемника и классическая формула (2) и релятивистская (4-1), т.е. урезанная до (4-4), дадут одинаковые результаты для среднего смещения длины волны (так же как и для средней частоты).

 

Вот теоретическое обоснование смещения средней длины волны из работы [24], где используется релятивистская формула (4-1), т.е. для движущегося приемника, но в виде для изменения длины волны, хотя для экспериментов Айвса здесь надо было использовать формулу (4-3) или (4-2), т.е. для движущегося источника излучения. А при использовании формулы (4-1), т.е. для движущегося приемника, надо было и в качестве классической формулы использовать формулу (2) для движущегося приемника, а не источника, как сделано в расчете. А в этом случае для длины волны при движении приемника формула (2) дает L=L0/(1-b1), т.е. при малых скоростях (b1<0,1), которые были у каналовых лучей, получается практически такое же смещение, как и по формуле (4-1). А автор вывода использует формулу (2) для движущегося источника, которая не дает смещения. Да, для частоты при движении приемника излучения (см. рис.2) у классической формулы будет линейная зависимость, но для длины волны она будет нелинейной и будет незначительно отличаться от релятивистской так же, как отличаются их графики на рис. 3 для частоты при движении источника сигнала, где уже для длины волны классическая формула даст как раз линейную зависимость.

 

Запишем релятивистскую формулу эффекта Допплера для длины волны

При движении источника под углами φ=0 и φ=π (противоположные направления) имеем соответственно

Если бы смещения λ₁' и λ₂' от λ были симметричны, т. е. λ₁'–λ=λ–λ₂', то среднее положение для двух смещённых линий совпадало бы с положением несмещённой линии λ. Но простой расчёт даёт

                        (2)

Отсюда видно, что теория относительности предсказывает несколько большее смещение в красную сторону, чем в фиолетовую, в отличие от классической теории, где

 

Но, эта путаница специалиста по СТО, который не знает чем отличаются формулы (4-1) и (4-3), при обосновании ассиметричного смещения dL не является роковой. Ведь, как мы выяснили выше, для продольного эффекта Доплера обе формулы (4-1) и (4-3) дают с математической точки зрения одинаковый результат. Смотрите ниже аналогичный расчет dL из работы [19], где используется формула (4-3), т.е. именно для движущегося источника, но получается то же самое асимметричное смещение в красную сторону от L0, хотя релятивистский множитель здесь дает эффект совершенно противоположный. И при этом здесь уже нет ошибки по нулевому смещению dL для классической формулы, т.к. график изменения длины волны здесь для движущегося источника будет именно линейный.

 

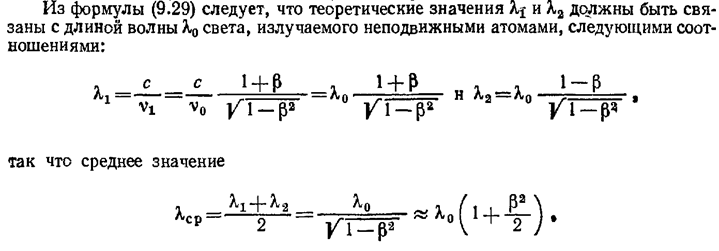
Но, если мы рассмотрим изменение частоты по формуле (4-3), где релятивистский множитель дает замедление времени на движущемся источнике, то мы получим точно такое же смещение средней частоты dv, как было для длины волны dL, но в синюю область. Посмотрите на рисунок 3 и вычислите по двум точкам на зеленой кривой, отражающей изменение частоты по формуле (4-3), изменение этой частоты для двух значений скоростей -0,7*b и +0,7*b и потом вычислите среднее смещение dv. Оно у Вас будет точно такое же, как и значение dL для длины волны вычисленное по темно-красной кривой, которая отражает изменение длины волны. Таким образом, это смещение в синюю область частоты излучения будет говорить об убыстрении времени на движущемся источнике, что противоречит выводу о замедлении времени, когда мы рассматривали ассиметричное смещение длины волны.

 

А, если мы при этом еще и вычислим с использованием классической формулы (2) ассиметричное смещение частоты в синюю область (при движении источника излучения) и ассиметричное смещение длины волны в красную область (при движении приемника), которые будут при b<0,1 практически такими же, как и у релятивистских формул, то мы сделаем вывод о том, что это ассиметричное смещение вообще никак не зависит от замедления времени, т.к. в классической формуле его вообще нет. Таким образом, это среднее смещение длины волны или частоты от исходного значения ни только ничего не говорит нам именно о замедлении времени на движущихся объектах, но и не всегда помогает доказать правильность именно релятивистской формулы. Поэтому, я вообще не понимаю, зачем надо было изобретать велосипед и морочить людям голову с теоретическим расчетом этих средних смещений.

 

Неужели, нельзя было, как делают все нормальные люди в таких случаях, нанести на график наблюдаемые значения смещений длины волны или частоты и построить расчетные зависимости по классической и релятивистской формулам. Я думаю, что, глядя на эти графики, даже школьник бы понял какая формула правильная. Тем более что после вычисления средних смещений их точно так же надо наносить на график и строить там же расчетные зависимости, чтобы на глаз определить какая из формул правильная. Ну, а, если ни по обычным смещениям, ни по средним смещениям на глаз не удается определить какая зависимость верная, то придется точно так же обрабатывать методом наименьших квадратов и те и другие значения, чтобы выяснить какая из формул более правильная. Не знаю, как Вам, а лично мне вся эта возня с расчетом средних смещений напоминает приемы мошенников, когда человека вводят в заблуждение по главному вопросу, сосредотачивая все его внимание на совершенно бесполезных вещах, т.е. на расчете этого среднего смещения, хотя, как мы видим, эти защитники СТО сами запутались в двух формулах (4-1) и (4-2).

 

Или вот, например, сторонники СТО приводят, как доказательство справедливости релятивисткой формулы эффекта Доплера, эксперименты по определению среднего смещения длины волны, выполненные Айвсом и Стилуэллом в 1938 [17] и 1941 [18] годах. Но при этом сторонники СТО забывают сказать, что Айвс при этом по значению dL хотел экспериментально подтвердить справедливость своей формулы (4-5) [16] для движения лучей света в эфире, чтобы объяснить отрицательный результат в опыте Майкельсона-Морли, т.к. являлся ярым противником СТО. И только позже, после интерпретации результатов этих экспериментов Джинсом с точки зрения СТО, все как-то стали воспринимать их эксперименты именно как подтверждающие замедление времени в СТО. А ведь, когда говорят не всю правду, а полуправду, то это тоже приемы мошенников, поэтому нам с Вами надо будет быть очень осторожными, когда мы будем разбирать эксперименты, которые якобы подтверждают справедливость релятивистской формулы эффекта Доплера в изложении современных сторонников СТО. Да, потом подобные эксперименты проводили и другие ученые, которые получили аналогичные результаты, но, как пишут авторы [21], заслуживают внимания, пожалуй, только эксперименты Айвса и Стилуэлла и Мандельберга и Виттена (выполненные в 1962 году), поэтому мы рассмотрим именно их. Далее для краткости я буду кругом писать Айвс и К или Мандельберг и К и т.д.

 

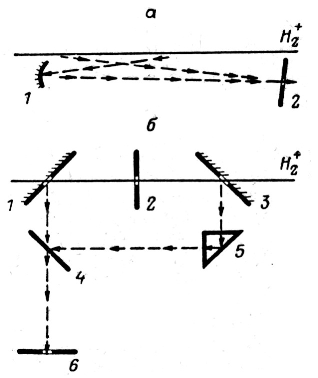
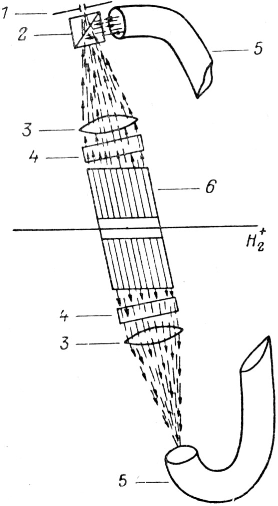
Рис. 6. Оптическая схема экспериментов Айвса (а) и Мандельберга (б) слева и Победоносцева справа.
Левый рисунок - а: 1 – зеркало, 2 – щель спектрографа; б: 1, 3 – зеркала, 2 – экран,
4 – полупрозрачное зеркало, 5 – призма, 6 – щель спектрографа. Правый рисунок - 1 – щель спектрографа, 2 – кубик Люммера, 3 – сферические линзы, 4 – цилиндрические линзы, 5 – гибкий световод, 6 – щелевой коллиматор света.

 

 

В обоих экспериментах авторы использовали каналовые лучи, т.е. разогнанные в электрическом поле ионы водорода Н2+ (два протона и один электрон), которые при столкновении с неускоренными молекулами водорода, которыми заполнялась установка, распадались на свободные протоны и возбужденные атомы водорода. В результате их же столкновений образовывались неподвижные атомы водорода в возбуждённом состоянии. Таким образом, как нам объясняют, в эксперименте должны наблюдаться три линии: несмещённая с длиной волны L0 (одна из линий серии Бальмера) и эта же линия с длинами волны L1 и L2, смещёнными вследствие эффекта Доплера при их наблюдении с разных направлений по отношению к движению пучка ионов. Принципиальные схемы их установок показаны на рис. 6, где Н2+ это движущийся слева направо пучок ионов. У Айвса и К на спектрограф напрямую попадало излучение из начала пучка ионов, т.е. приближающихся к спектрографу, а излучение от ионов при удалении их от спектрографа попадало на него из конца пучка ионов, отразившись от сферического зеркальца. А у Мандельберга и К, при движении ионов так же слева направо, излучение от начала пучка до экрана попадало на левое зеркало 1, а от экрана до конца пучка попадало на правое зеркало 3, т.е. от зеркала 3 излучение было по ходу движения ионов, а от зеркала 1 против их движения и далее, отраженные от зеркал излучения, с помощью зеркала и призмы попадали на щель спектрографа.

 

Принципиальным недостатком этих установок является то, что излучение в прямом и обратном направлениях имеет немного разные по абсолютной величине скорости, т.к. ионы при движении в разряженном водороде хоть немного, но тормозятся. А кроме этого у них излучение регистрируется под углом к скорости пучка, хотя у Мандельберга и К эти углы и очень близки к 0 и 180 градусам. Ну, и, естественно, у них были очень маленькие скорости ионов, т.к. максимальное напряжение у Айвса и К было 42,28 кВ, а у Мандельберга и К 78 кВ, что для ионов водорода Н2+ при их массе 3,3509*10^-27 кг даст скорости 0,00671*с и 0,00911*с. При этом Айвс и К использовали и ионы Н3+, но они при большей массе дадут еще меньшую скорость.

 

Недостатки установок Айвса и Мандельберга были устранены в установке Победоносцева и К [21] в 1989 году, схема которой дана на правом рис. 6 и где мы наблюдаем общий эффект Доплера. Для того чтобы излучение в прямом и обратном направлениях происходило из одного и того же участка ионов, они применили щелевой коллиматор, который был установлен под углом в 77 градусов к оси пучка ионов. В результате излучение по ходу движения ионов было под углом в 77 градусов к пучку, а в противоположную сторону под углом в 257 градусов. Таким образом, здесь при расчете релятивистского множителя надо учитывать полную скорость пучка ионов, а в остальной части формулы (4-3) V*cos(77). Существенным было так же то, что у них установка позволяла разгонять ионы до энергии 2000 кэВ, что позволяло получать скорость ионов 0,04613*с и то, что они использовали для калибровки спектрограмм подсветку неоном, который давал вблизи изучаемой ими несмещенной линии излучения ионов водорода Н2+ с длиной волны 6562,8 А (652,28 нм) еще три полосы.

 

Да, Айвс и К хоть и подтвердили эффект замедления времени на движущемся источнике, что и требовалось Айвсу для объяснения отрицательного результата в опытах Майкельсона-Морли согласно его формуле, но достоверность их экспериментальных данных и ранее вызывала много вопросов и вызывает сейчас. Например, уже в 1939 году Оттинг критиковал их и за сферическое зеркальце, которое при конечной ширине пучка излучения приводило к нелинейной зависимости от угла падения на него излучения и за то, что у них было слишком большое время освещения фотопластин и они не фотометрировались. Да и Джонс в том же 1939 году писал о том, что из-за того, что, якобы неподвижные атомы водорода, могут увлекаться пучком ионов и иметь некоторую положительную скорость, центральная линия может смещаться в синюю сторону и это приведет к завышенному значению асимметричного смещения от центральной линии в красную сторону. Причем, при некоторых условиях такая погрешность может быть порядка величины наблюдаемого эффекта. Поэтому во второй их работе 1941 года, где Айвс и К приводят результаты уже с энергией частиц до 42,28 кэВ, они уделили очень много внимания замечаниям сделанным Оттингом и Джинсом.

 

Но вот, как пишут Победоносцев и К, только за счет того, что излучение в прямом направлении и обратном у них бралось из разных участков пучка ионов, то за счет замедления ионов в атмосфере водорода, напускаемого в рабочую область установки, скорость ионов в обратном направлении будет меньше, чем в прямом. А при тех напряжениях разгона ионов, что они использовали (до 43 кВ), это может дать погрешность сопоставимую с самим эффектом, и, например, при напряжении до 34 кВ погрешность будет даже больше самого эффекта асимметрии в смещении линий. Поэтому ни о какой достоверности этих данных, при такой грубой ошибке в методике проведения экспериментов, не может быть и речи. А мне, к тому же, не нравится и то, как Айвс и К учли угол отклонения скорости пучка ионов от скорости излучения в 7 градусов. В работе [17] (см. табл.1) они приняли, что истинные наблюдаемые данные будут равны полученным наблюдаемым даным деленным на cos(7), но это не правильно, т.к. в наблюдательных данных мы фиксируем полный результат, а угол надо учесть только в части эффекта. Поэтому наблюдаемые данные надо было оставить в покое, а вот для расчетных данных надо было для релятивистского множителя в формуле (4-3) взять полную скорость пучка ионов, а скорость отвечающую только за сам эффект Доплера надо было умножить на cos(7). Да, тут у нас появляется погрешность в 2 %, которая не может повлиять принципиально на результаты экспериментов, но такая элементарная ошибка в обработке данных уже подрывает доверие к полученным результатам.

 

Давайте теперь рассмотрим экспериментальные данные Победоносцева и К. Сразу замечу, что у меня ни к методике проведения экспериментов ни к экспериментальной установке замечаний нет, если не считать того, что они не определяли скорость каналовых лучей непосредственным измерением, а рассчитывали, как и все, по энергии V=sqrt(2*E/m). В том виде, как авторы статьи изложили эти данные, когда они дали ошибку по расчету относительной разности отклонений длин волн в красную и синюю стороны при противоположных углах наблюдения, где ошибка получается почти 50%, ясно видно, что их данные не подтверждают релятивистскую формулу (4-2). Правда при этом, они в статье подчеркнули, что сейчас никто не сомневается в справедливости релятивистской формулы (наверное, чтобы пропустили статью в печать), а расхождения с наблюдательными данными можно объяснить неясностью с процессами излучения в атомах. А вот с этим объяснением я частично согласен и поэтому, прежде чем использовать в экспериментах по эффекту Доплера процессы излучения, надо бы сначала хорошенько разобраться с самими процессами излучения.

 

И с разгоном частиц в ускорителях тоже не мешало бы разобраться, а то используем при проведении экспериментов скорости частиц, рассчитанные по энергии затраченной на их разгон, и совершенно не учитываем КПД этих ускорителей. А в результате получаем частицы с огромными энергиями, но со скоростями всегда меньше скорости света, что зачем-то объясняют мифическим увеличением массы частиц с ростом скорости. Но почему-то это увеличение массы при рассмотрении экспериментов с излучением частиц никак не учитывают при расчете частот излучения. И, если мы, например,  посмотрим на абсолютные значения отклонений в эксперименте Победоносцева и К (см. табл.1), то мы увидим, что все расчетные данные, как по классической формуле, так и по релятивистской, получились немного больше, чем наблюдаемые значения. Таким образом, это может быть косвенным доказательством того, что при разгоне частиц в электрическом поле КПД ускорителей всегда меньше 100%. Но, даже, если бы в экспериментах Айвса и К замерялась скорость каналовых лучей непосредственно пролетным методом, то эти эксперименты все равно являются явно не корректными, поэтому не могут ничего доказать в принципе. А вот экспериментальные данные полученные Победоносцевым и К могли бы быть использованы для подтверждения релятивистской формулы для эффекта Доплера, но при непосредственном замере скорости каналовых лучей, а этого не делалось. Таким образом, все эксперименты с каналовыми лучами не могут пока подтвердить ни релятивистскую формулу ни классическую. 

 

Правда, недавно появились новые экспериментальные данные, которые получили ученые из Германии [7, 25, 26, 40, 41, 43] и которые подтверждают справедливость релятивистской формулы для чисто продольного эффекта Доплера. Они ионы лития 7Li+, разогнанные в ускорителе, помещали в специальное кольцо сложной конфигурации длиной 55,4 м, где они вращались в вакууме по инерции, удерживаемые магнитным полем (см. левый рис. 7). Затем, на прямолинейном участке движения ионов, они облучались двумя лазерами, свет от которых подводился по оптоволокну, в попутном направлении движения пучка ионов с частотой vp и навстречу пучку с частотой va.

 

 

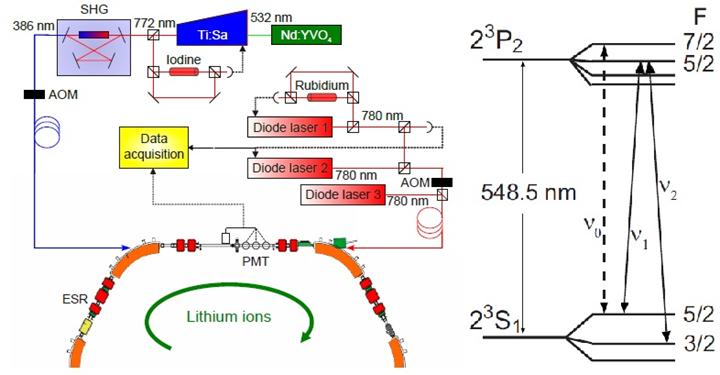
Рис. 7. Схема установки для трехуровневого ДОР слева (воспроизведено из работы [25]) и схема переходов между энергетическими уровнями для двухуровневого ДОР насыщения и трехуровневого линейного ДОР по Л-схеме справа (воспроизведено из работы [7]).

 

 

В возбуждённом состоянии, т.е. на верхнем уровне, ионы находятся очень короткое время (43 нс) после чего происходит спонтанное излучение, т.е. обратный переход в невозбуждённое состояние на нижний метастабильный уровень, где они могут находиться около 50 с, и в этот момент возникает флуоресценция (свечение, которое распространяется в произвольном направлении). Сама частота флуоресценции в эксперименте не определялась, а просто тремя датчиками PMT (фотоумножители) под углом 90 градусов к направлению движения пучка ионов фиксировалась её интенсивность (крайние датчики регистрировали излучение при воздействии на ионы одного лазера, а средний при воздействии на ионы обоих лазеров). При этом они проводили два типа экспериментов. В Хидельберге, где они разгоняли ионы ускорителем Ван де Граафа до скоростей 0,03*с и 0,064*с и затем помещали в накопитель (кольцо) TSR, они наблюдали двухуровневый двойной оптический резонанс (ДОР) в режиме насыщения, а в Дармштадте (на рис. 7 показана эта установка), где они разгоняли ионы на циклотроне до скорости 0,338*с и затем помещали в накопитель ESR, они наблюдали трехуровневый ДОР по Л-схеме. Правда, авторы пишут, что они наблюдали во втором варианте оптическо-оптический двойной резонанс, но это и есть ДОР. Бывает еще двойной резонанс радиочастотно-оптический, микроволново-оптический и инфрокрасно-оптический, но у авторов эксперимента в обоих вариантах был именно ДОР.

 

 

При использовании двухуровневой схемы у нас при возбуждении электронов происходит их переход с уровня s1 (F=5/2) на уровень p2 (F=7/2), как это показано на правом рис. 7,  с последующим спонтанным излучением волны 548,47 нм (есть такая стандартная длина волны для иона лития [39]), т.е. с частотой v0=546,593 * 10^12 Гц при скорости света 299790 км/с). Правда, авторы, почему то, пишут, что длина волны будет 548,5 нм, т.е. с их скоростью света 299737 км/с у них получается частота v0=546,467 * 10^12 Гц, поэтому я далее буду использовать их данные. Таким образом, как пишут авторы, чтобы происходило излучение на частоте v0, надо чтобы частоты лазеров, светящего по ходу движения пучка ионов, vp=582,491 * 10^12 Гц и, светящего во встречном направлении, va=512,671 * 10^12 Гц после преобразования согласно релятивистской формуле эффекта Доплера для движущегося приемника при скорости пучка ионов 0,064*с, воздействовали на ионы в их системе отсчета с частотой v0 (назовем такую частоту лазеров эффективной частотой) и возбуждали электроны, переводя их на верхний уровень. А вот при использовании трехуровневой схемы у них поглощение или излучение происходят при переходах электронов между уровнями s1 (F=5/2) <--> p2 (F=5/2) и s1 (F=3/2) <--> p2 (F=5/2) при эффективных частотах возбуждения v11=546,455 * 10^12 Гц и v22=546,475 * 10^12 Гц, которые получатся при скорости пучка ионов 0,338*с от воздействия одним лазером с длиной волны 386 нм (vp=777,210 * 10^12 Гц) по ходу движения пучка ионов и другим лазером с длиной волны 780 нм (va=384,226 * 10^12 Гц) во встречном направлении.

 

 

Первый вариант экспериментов называется спектроскопией насыщения потому что ДОР наблюдается на нелинейном участке эффективности воздействия лазера, когда дальнейшее увеличение мощности лазера практически не приводит к увеличению интенсивности излучения (см. рис. 9б, где показана интенсивность излучения при работе одного лазера и двух лазеров одинаковой мощности). При этом, обычно, вещество облучают двумя лазерами во встречных направлениях (основным мощным, которым насыщают верхний энергетический уровень, и сканирующим маломощным). Скорости различных групп атомов всегда будут отличаться от скорости центральной группы (наиболее многочисленной) как в положительную так и в отрицательную стороны поэтому из-за эффекта Доплера эффективные частоты, совпадающие с частотой линии поглощения, для различных групп атомов будут различные. Таким образом, при облучении большой группы атомов различными частотами (близкими к частоте линии поглощения для скорости центральной группы атомов) мы наблюдаем доплеровски уширенную линию поглощения. И точно так же будет уширена линия при излучении атомом на одной и той же частоте, соответствующей своей естественной линия излучения (см. рис. 8в и правый рис.10), а ширина этой линии для видимого света на два порядка шире естественной линии излучения. При этом ширина доплеровски уширенной линии (или просто ширина линии) измеряется на полувысоте ее профиля интенсивности излучения, поэтому на графиках, обычно рисуют ее спектр поглощения или излучения на интервале частот только немного шире профиля на полувысоте интенсивности излучения.

 

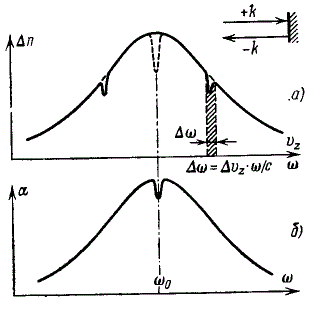
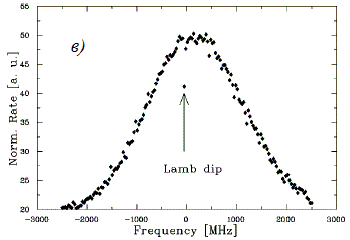
Рис. 8. а) симметричные провалы Беннета в распределении населенности нижнего уровня в случае облучения атомов вещества двумя встречными волнами, когда частота v11 не равна v22. б) Лэмбовский провал коэффициента поглощения в центре доплеровского уширенного профиля линии поглощения при v11= v22 (воспроизведено из работы [27], где используется круговая частота w). в) Изменение суммарной интенсивности излучения в эксперименте двухуровнего ДОР со скоростью ионов 0,064*с, где ширина линии получается 2,8 ГГц, при изменении частоты сканирующего лазера влево и вправо от va (воспроизведено из работы [41]).

 

 

А при облучении пучка ионов двумя встречными лазерами, когда их эффективные частоты совпадают с частотой линии поглощения для скорости центральной группы атомов, которая в нашем случае будет средней скоростью пучка ионов, на доплеровском профиле наблюдается провал Лэмба (см. рис. 8б и 9а). Но, если эффективная частота сканирующего лазера совпадает с частотой линии поглощения для группы атомов, скорость которой отличается от скорости центральной группы атомов, то в данном случае наблюдается провал Беннета (см. рис. 8а), которых может быть два, как для группы, скорость которой больше скорости центральной группы, так и для группы со скоростью меньше центральной. Поэтому обычно, при покоящемся исследуемом веществе, для получения провала Лэмба используют один лазер, у которого луч расщепляют на два встречных, один из которых ослабляют, и при этом эффективные частоты у обоих лучей будут совпадать точно и именно с центральной группой атомов, т.е. с той, где скорость равна нулю.

 

 

А, судя по графику интенсивности излучения для полосы частот чуть больше половины ширины доплеровского профиля линии излучения (см. рис. 8в), в эксперименте наблюдался не совсем провал Лэмба и сами авторы эксперимента надеялись увидеть что то похожее на график рис. 9а. И хотя в эксперименте провал наблюдается не ровно по центру пика доплеровской ширины линии излучения ионов лития, а смещеным от этого пика влево, но возможно, что это действительно провал Лэмба, а расчетные частоты лазеров просто не соответствовали эффективной частоте для скорости ионов в середине пучка. Вот только, как я понял, на графике (см. рис. 8в) у нас отражена не суммарная интенсивность излучения, а за вычетом интенсивности излучения, вызванной работой основного насыщающего лазера с постоянной частотой vp, т.к. график начинается с нуля интенсивности, а должен был начинаться с интенсивности основного лазера, как показано на рис. 9а. Ведь основной лазер постоянно возбуждает электроны центральной скоростной группы ионов и датчик PMT3 должен при любой частоте сканирующего лазера, возбуждающего по очереди все скоростные группы ионов, регистрировать излучение как от основного лазера так и вызванное работой сканирующего лазера.

 

 

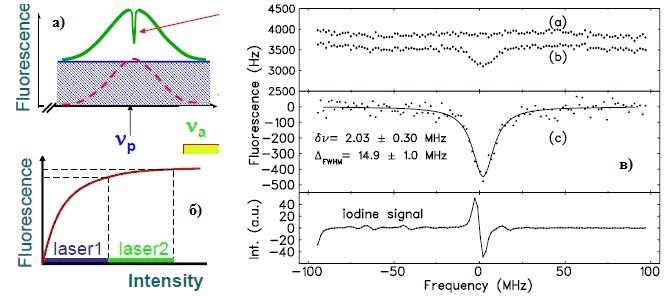
Рис. 9. а) - теоретическая форма провала Лэмба. б) - зависимость интенсивности излучения при возбуждении атомов от мощности одного лазера или суммы мощностей двух одинаковых лазеров в режиме насыщения, т.е. на нелинейном участке характеристики (воспроизведено из работы [41]). в) интенсивность излучения ионов лития при скорости пучка 0,064*с при облучении их двумя встречными лазерами и с изменением частоты одного из них от нулевого значения (соответствующего опорной линии йода) на интервале 200 МГц, где a) арифметическая сумма интенсивностей излучения при раздельной работе двух лазеров, b) интенсивность излучения при одновременной работе двух лазеров, с) разность интенсивностей b) и a) (воспроизведено из работы [26]).

 

 

А вот зачем авторы этого эксперимента с ДОР насыщения вычисляют арифметическую сумму интенсивностей излучения при работе лазеров по отдельности, а затем вычитают ее из суммарной интенсивности излучения при работе двух лазеров одновременно, как это мы видим на рис. 9в и при этом мощность сканирующего лазера берут такой же, как и насыщающего, т.е. рассматривают вариант образования провала Лэмба, который возникает в самих лазерах, это вообще не понятно. Во-первых, при спектроскопии насыщения ничего вычитать не надо и глубина и ширина провала Лэмба измеряются непосредственно по графику b), а, во-вторых, арифметически складывать интенсивности при работе лазеров по отдельности вблизи провала Лэмба нельзя, т.к. спектроскопию насыщения называют так же нелинейной оптикой. Да авторы и сами приводят график изменения интенсивности излучения с ростом мощности лазера (см. рис. 9б). Правда, они здесь нарисовали, что будут параллельно работать два одинаковых лазера, как у них и было в эксперименте, но более корректно здесь по оси абсцисс отложить просто мощность одного лазера. Так вот, с ростом мощности лазера у нас при обычном резонансе сначала линейно растет интенсивность излучения (линейная спектроскопия), а потом при приближении к зоне насыщения график становиться нелинейным и рост мощности лазера практически не увеличивает интенсивность излучения, т.к. заселенности верхнего и нижнего уровней становятся примерно одинаковые.

 

 

Если в нашем эксперименте (при одинаковой мощности лазеров) фазы обоих лазеров для центральной скоростной группы ионов совпадают, то у нас будет небольшое увеличение интенсивности излучения, а, если лазеры будут работать в противофазе, то у нас интенсивность излучения упадет до нуля, но вероятность этих обоих вариантов практически равна нулю. Поэтому всегда будет некоторое рассогласование фаз и у нас сканирующий лазер будет за один период колебаний и немного увеличивать интенсивность излучения, когда амплитуды излучения лазеров будут суммироваться, и много уменьшать, когда суммарная амплитуда воздействия будет уменьшаться, а в результате за один период у нас немного уменьшится интенсивность излучения, что и даст провал Лэмба. И авторам эксперимента надо было просто зафиксировать этот момент, а не вычислять ширину провала добиваясь какой то фантастической точности в определении частоты середины провала как будто они уточняют до восьмой значащей цифры какую то физическую константу, например, гравитационную постоянную.

 

 

А их манипуляции с арифметическим сложением интенсивности излучения от двух лазеров работающих по отдельности говорят только о том, что у них в этом эксперименте что-то было не ладно. Если мы, согласно их же графика (см. рис. 9б), арифметически просуммируем интенсивность излучения от работы двух лазеров одинаковой мощности, которые большей частью будут работать на линейном участке характеристики, то это даст почти двойную интенсивность излучения по сравнению с интенсивностью излучения одновременно работающих двух лазеров даже при их работе в одной фазе. А согласно их данным арифметическая сумма интенсивностей излучения получается примерно 3900 Гц, а суммарная интенсивность при одновременной работе двух лазеров примерно 3600 Гц. Таким образом, я не знаю что там за эффект наблюдали авторы этого эксперимента (вариантов тут масса), но это в любом случае не ДОР насыщения с образованием провала Лэмба. Хотя, возможно, что мощность сканирующего лазера у них, как и положено делать в таких экспериментах, была меньше мощности основного, а тогда интенсивность излучения на графиках "a" и "b" будет похожа на правду, но в любом случае ничего суммировать тут не надо.

 

 

Более того, схема установки у них немного отличалась от той, что нарисована на рис. 7, а именно у них лучи обоих лазеров подводились к кольцу с пучком ионов по одному оптоволокну, как это показано на левом рис. 10, где они входят в кольцо слева, отразившись от поворотного зеркала. Затем два луча проходили через встречный поток ионов слева направо, где отражались от правого зеркала и опять направлялись на пучок ионов в попутном направлении. Таким образом, в этом варианте эксперимента у нас на пучок ионов, кроме двух эффективных частот v0, которые получаются при воздействии сканирующего лазера с частотой va=512,671 * 10^12 Гц и светящего во встречном направлении при первом проходе пучка и лазера накачки с частотой vp=582,491 * 10^12 Гц, светящего на пучок в попутном направлении после того, как он отразиться от правого зеркала, т.е. при втором проходе, действовали еще две эффективных частоты, которые получатся при движении луча с частотой va в попутном направлении (после отражения от зеркала) и при движении луча с частотой vp во встречном направлении при первом проходе. К тому же, совершенно не понятно почему в этом эксперименте ослабляется не луч сканирующего лазера, а луч основного лазера, т.е. лазера насыщения, который с частотой vp воздействует на ионы, сначала пройдя через весь пучок и отразившись от правого зеркала. В общем, получается очень запутанная ситуация с образованием тут провала Лэмба.

 

 

 

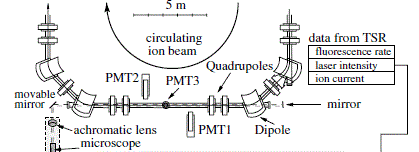
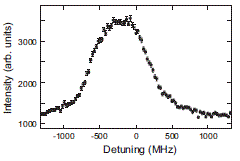
Рис. 10. Слева - схема части кольца TSR с расположением датчиков излучения PMT1...PMT3 (воспроизведено из работы [26]). Справа - интенсивность излучения ионов лития при скорости пучка ионов 0,338*с при облучении их одним лазером с изменением его частоты от нулевого значения соответствующего длине волны 780 нм на интервале частот чуть больше доплеровской ширины линии излучения, которая составляет здесь 1 ГГц  (воспроизведено из работы [7]).

 

 

А теперь давайте перейдем к трехуровневому ДОР. На рис. 7 (справа) они привели для этого эксперимента Л-схему, а, вообще то, трехуровневые ДОР бывают и по V-схеме с общим нижним уровнем (см. рис. 11а) и по каскадной схеме с общим промежуточным уровнем (см. рис. 11б). При этом эффективные частоты в трехуровневых ДОР могут отличаться очень сильно, т.к. назначение этих схем возбуждение самых разнообразных уровней. А для нашего эксперимента, я думаю, лучше всего подошла бы каскадная схема, когда первый лазер с эффективной частотой v11 заселяет 2-ой уровень, а второй лазер с эффективной частотой v22 (или одновременно или с некоторой задержкой по времени) переводит электрон с этого уровня на уровень "а", где и происходит спонтанное излучение с частотой v12= v11+v22. Этой схеме эквивалентна (при одновременном облучении двумя лазерами) схема двухфотонного ДОР с реальным промежуточным уровнем "k" (см. рис. 11в), когда у нас электрон получает сразу два фотона с энергиями h*v11 и h*v22. Но можно использовать и фиктивный уровень "v" (см. рис. 11г), т.к. самое главное при двухфотонном ДОР, чтобы сумма двух эффективных частот давала энергию необходимую для перехода на уровень "f", где будет происходить спонтанное излучение (флуоресценция), которую мы и будем фиксировать.

 

 

 

Рис. 11. Двухуровневые схемы для двойного оптического резонанса. а) V-схема с общим нижним уровнем. б) каскадная схема. в) двухфотонная с реальным промежуточным уровнем. г) двухфотонная с фиктивным промежуточным уровнем (воспроизведено из работы [27]).

 

 

Таким образом, у нас во втором эксперименте возможно, что был или каскадный ДОР или двухфотонный ДОР, а в этом случае резонансная частота излучения будет уже v1+v2. Если справедлива релятивистская формула для эффекта Доплера, то мы получим частоту 1092,929*10^12 Гц (длина волны 274,3 нм), а, если справедлива классическая формула, то мы получим частоту 1028,607*10^12 Гц (длина волны 291,454 нм). Для длины волны 274,3 нм в спектре излучения 7Li+ имеется две близкие линии 273,07 нм и 276,7 нм, а для линии 291,454 нм тоже есть близкая линия 295,27 нм [39], поэтому вполне возможно, что в эксперименте наблюдали резонанс и на этих частотах, но проверить это мы не можем, т.к. авторы эксперимента упорно отказываются измерять частоту флуоресценции. К тому же, хотя мы и видим на левом рис. 12 всплеск интенсивности излучения при работе двух лазеров одновременно, когда на верхний уровень p2 (F=5/2) электроны закачиваются и с уровня s1 (F=3/2) и с уровня s1 (F=5/2), но мы никак не можем гарантировать, что закачка произошла именно с этих уровней и именно на уровень p2 (F=5/2). Ведь различных подуровней, как на нижнем, так и на верхнем уровне, очень много (см. правый рис. 12) и расположены уровни очень часто поэтому, даже, если мы и неправильно рассчитали частоты лазеров va и vp, то мы все равно загоним электрон с какого ни будь нижнего подуровня на какой ни будь верхний подуровень. После этого точно так же произойдет спонтанное излучение и датчики будут считать эти импульсы излучения, как ни в чем не бывало, т.к. им все равно какая была длина волны при излучении, а при совпадении суммы двух частот с одной из резонансных частот в спектре иона лития у нас добавиться и излучение от двухфотонного поглощения.      

 

 

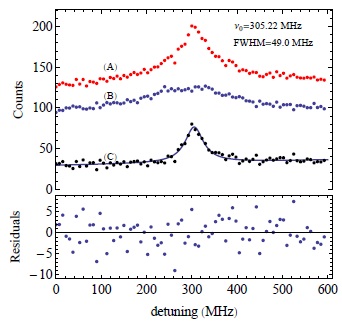
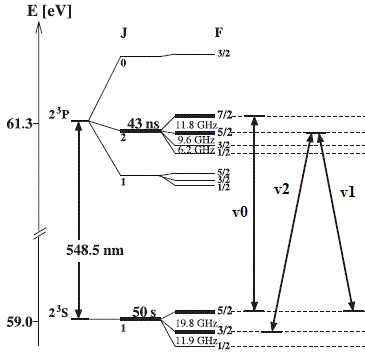
Рис. 12. Левый рисунок - изменение интенсивности спонтанного излучения (флуоресценции) при ДОР по Л-схеме, когда частота одного лазера остается постоянной, а сканирующего изменяется. А- изменение интенсивности излучения при одновременной работе двух лазеров. В- сумма двух интенсивностей при работе лазеров по одному. С- разница интенсивностей С=А-В (воспроизведено из работы [25]). Правый рисунок - часть энергетических уровней и подуровней иона лития, используемая в экспериментах двухуровнего ДОР с частотой v0 и трехуровнего ДОР с частотами v1 и v2 (воспроизведено из работы [40]).

 

 

Но авторы эксперимента [7] настаивают, что здесь у них не только будут рассчитанные ими эффективные частоты, но и на том, что всплеск интенсивности излучения будет, потому что эффективные частоты для левой и правой ноги Л-схемы будут качать "туда и сюда" электроны по обоим переходам для одной и той же центральной скоростной группы ионов. А вот это я совсем не понимаю, т.к. нет никакой разницы из какой скоростной группы лазеры на разных переходах будут возбуждать электроны. Нижние уровни между собою никак не связаны (даже у одной и той же скоростной группы на двух нижних уровнях будут совершенно разные электроны) и, следовательно, главное, чтобы эффективная частота лазера совпала с частотой этого перехода, а для какой скоростной группы это произошло не имеет никакого значения. И совершенно не понятно, с какого перепугу электроны начнут бегать "туда и сюда". Туда они будут бегать, т.к. будут резонансно возбуждаться на конкретной частоте, а вот сюда они не обязаны возвращаться, т.к. при спонтанном излучении они могут спокойно улететь на любой (не запрещенный) нижний уровень.

 

 

При этом авторы эксперимента опять, зачем-то, суммируют излучение от двух лазеров при их работе по отдельности и потом из суммарной интенсивности излучения вычитают арифметическую сумму интенсивностей, как это делали и в первом варианте экспериментов. Ну и о чем это нам говорит и что это нам дает. Только то, что здесь опять, что-то не ладно в Датском королевстве, т.к., вследствие того, что оба лазера у нас здесь работают на линейном участке характеристики (см. рис. 9б), и работают они параллельно, т.е. с разными электронами, находящимися на разных нижних уровнях, то у нас здесь на всей ширине линии поглощения арифметическая сумма излучений при работе лазеров по отдельности должна быть точно равна суммарному излучению при работе двух лазеров одновременно. А в эксперименте мы явно видим, что графики A и B не совпадают. Естественно, при работе этой схемы все будет работать так, как пишут в учебниках, только, если электроны будут с верхнего уровня возвращаться каждый на свой нижний уровень и при этом еще и не будут утекать на какой ни будь другой нижний уровень, а иначе появятся нелинейности в интенсивности излучения одного или сразу двух переходов, как при режиме насыщения.

 

 

Но я надеюсь, что т.к. время воздействия лазеров на ионы пучка было непродолжительное то заселенность нижних уровней за это время должна измениться незначительно, а за счет столкновений ионов за время обращения по кольцу населенности нижних уровней опять выровняются и оба лазера все же будут работать на линейных участках. Однако, описанный мною вариант развития событий, как показывает практика, будет наблюдаться только при небольших мощностях лазеров, а у нас тут мощность лазера с постоянной частотой была очень даже приличной (280 мВт). А в этом случае у нас возможен и другой вариант развития событий, т.е. эффект квантового пленения населенностей (КПН) или так называем темный провал. Этот эффект возникает при работе по трехуровневой Л-схеме с близко расположенными двумя нижними подуровнями, т.е. то, что и было у нас во втором эксперименте. При этом (см. левый рис. 13), если интенсивность лазеров небольшая, то у нас получается обычная доплеровски уширенная линия поглощения (кривая 1), т.е. тот вариант развития событий, что я описал выше, а с увеличением интенсивности излучения начинает образовываться темный провал (кривые 2, 3, 4).

 

 

 

 

Рис. 13. Слева - образование темного провала при фиксированной частоте одного лазера и изменении частоты сканирующего лазера, т.е. уменьшения населенности верхнего уровня, где и происходит спонтанное излучение. Здесь частоты Ω1= v1-v11 и Ω2= v2 - v22 (воспроизведено из работы [42]). Справа - схема устройства для изменения скорости пучка ионов в кольце (воспроизведено из работы [43]).

 

 

Внятного теоретического объяснения этому явлению, как я понял, сейчас нет, т.к. объяснения в духе "возникновения непоглощающей суперпозиции состояний атома" или "особым когерентным состоянием системы, когда амплитуды вероятностей нижних состояний имеют противоположные знаки", лично мне ничего не объясняют. Да и книжное объяснение образования провала Лэмба вследствие образования стоячей волны я считаю просто смешным, поэтому выше я и дал свое объяснение этому эффекту. А вот с темным провалом я не могу дать такого простого объяснения его образования и могу только предположить, что при этом электроны начинают раскачиваться вдоль радиуса с частотой v12= v1 - v2 и это затрудняет возникновения резонанса на частотах переходов v1 и v2. Тем ни менее это не отрицает факта того, что темные провалы реально наблюдаются в экспериментах. А вот почему мы не наблюдаем этого провала в нашем втором эксперименте, а наблюдаем наоборот всплеск интенсивности, в этом надо долго разбираться, а не делать скоропалительных выводов, как авторы наших экспериментов, которые все, что не наблюдают, объясняют мифическими эффектами даже не вникая в суть происходящего.

 

 

При этом расположение датчиков в этих двух экспериментах не всех в одном месте, а разнесенных по ходу движения пучка ионов, меня вообще ставит в тупик. В этих экспериментах лучи лазеров перед попаданием в оптоволоконный кабель проходят через акустическо-оптикие модуляторы (АОМ) и поэтому в кольцо с ионами подается или луч от одного лазера или луч от другого лазера или оба луча сразу или ничего на интервалах по 200 мкс в первых экспериментах и по 100 мкс во втором, поэтому и нужный датчик работает только в нужный ему интервал времени. Следовательно, даже если расположить все датчики в одном месте они будут регистрировать именно то, что им надо. При этом, если в первых экспериментах расположение датчиков не в одном месте из-за малой скорости пучка ионов не сильно скажется на нелинейности результатов работы датчиков, то при скорости 0,338*с это станет очень заметно.

 

 

Если предположить, что на рис.7 эта часть установки с датчиками имеет те же размеры, что и на левом рис. 10, то расстояние от того места, где пучок ионов выходит на прямолинейный участок и начинает облучаться лазерами, до 3-го датчика, который фиксирует излучение при одновременной работе двух лазеров, составляет около 5 м. Пучок ионов проходит его за 49 нс, а расстояния до датчиков 1 и 2 примерно за 34 нс и 64 нс. А отсюда получается, что, т.к. в возбужденном состоянии электроны находятся 43 нс, то первый датчик должен вообще ничего не регистрировать, а 3-ий и 2-ой будут регистрировать излучение от электронов, которые возбуждались менее 6 нс и менее 31 нс. Естественно, при всех прочих условиях 2-ой датчик будет регистрировать больше всего импульсов и поэтому здесь возникает нелинейность в счете только от расположения датчиков. Следовательно, ничего суммировать или вычитать из показаний этих датчиков, как делали авторы эксперимента, нельзя и по этой причине. В общем, здесь по графикам A и B очень большой вопрос.

 

 

Таким образом, мы видим, что вопросов только по спектроскопии, как к первому варианту экспериментов, так и ко второму, накопилось очень много, и поэтому меня удивляет, как авторы этих экспериментов, у которых должны были возникнуть те же вопросы, не выяснив причину расхождения наблюдаемых явлений тому, что обычно наблюдают при проведении подобных экспериментов, решились утверждать, что их эксперименты подтверждают релятивистскую формулу для эффекта Доплера. И, в связи с возникшими вопросами, меня просто удивляет то, что ни один из почти 20 соавторов эксперимента, так и не додумался за все 10 лет измерить частоту излучения флуоресценции. Ведь полученные ими результаты вполне могли получиться и при неправильном расчете частот лазеров и при неправильном определении скорости пучка ионов или при возникновении и двухфотонного резонанса, а измеренная длина волны излучения (или нескольких разных, которые могли быть в этих экспериментах) заставила бы их сразу задуматься о том, почему получилось именно так. Или возможно, что, если бы авторы провели вторые эксперименты и со скоростью 0,45*с (как я понял, установка позволяет это сделать), то они получили бы результаты, которые бы тоже заставили их задуматься, но и этого не было сделано. И потом, почему мы не видим результата, который бы наблюдался при расчете частот лазеров по классическому эффекту Доплера. Возможно, что и в этом случае они наблюдали бы похожую картину и задумались бы, наконец-то, над методикой проведения своих экспериментов.

 

 

А вот то, как в экспериментах определялась скорость пучка ионов, это очень интересно. Дело в том, что при больших скоростях ионов вычислять эту скорость по затраченной на разгон энергии нельзя, т.к. КПД ускорителей при таких скоростях будет явно меньше 100%. И если при разгоне ионов до скорости 0,064*с они затрачивали в ускорителе Ван де Граафа энергию 13,3 МэВ, что при массе ионов 11,7196*10^-27 кг по формуле V=sqrt(2*E/m) дает 0,0636*с, т.е. КПД получается примерно 100%, то при разгоне до скорости 0,338*с это будет не так. Они затрачивали при разгоне ионов на циклотроне 58,6 МэВ на нуклон, что по той же формуле при семи нуклонах у 7Li+ даст  скорость 0,353*с, что заметно больше 0,338*с, поэтому скорость надо было определять при эксперименте непосредственно пролетным методом. Тем более что установка позволяет это сделать (имеются большие прямолинейные участки кольца).

 

 

А как же авторы эксперимента определили, что у них была скорость именно 0,338*с, если им неизвестен КПД ускорителя и они не замеряли скорость пролетным методом. А делалось это так. После того, как ионы впрыскивались в кольцо, они в течение 7-20 с охлаждались в электронном охладителе, где обдувались электронами, чтобы уменьшить разброс скоростей ионов в пучке и уменьшить ширину линии, а потом на две пластины (см. правый рис. 13) в этом же охладителе подавалось напряжение (на 3-ей гармонике предполагаемой частоты обращения ионов по кольцу TSR и на 10-ой гармонике для кольца ESR), которое изменяло скорость ионов в кольце. И в тот момент, когда при работе лазера с постоянной частотой vp наблюдалась флуоресценция, напряжение отключали, т.к. считали что скорость пучка достигла 0,338*с, при которой эффективная частота согласно расчету по релятивистской формуле для эффекта Доплера как раз и возбуждала переход, который был нужен в эксперименте [7].

 

 

И получается, что авторы эксперимента определяют скорость пучка ионов по релятивистской формуле для эффекта Доплера, а потом доказывают экспериментально справедливость релятивистской формулы для эффекта Доплера, что, мягко говоря, не корректно. Таким образом, т.к. неизвестно на какой переход при этом попали авторы эксперимента, то определение таким образом скорости пучка становиться неоднозначным, а, если справедлива формула для классического эффекта Доплера, то скорость получается совершенно не определенной и вариантов развития событий в этом эксперименте становиться очень много. Поэтому, даже, если с теоретической точки зрения авторы эксперимента делали все так, как их учили, то все равно надо было скорость после этих манипуляций измерять непосредственно. Тем более, как я понял, не очень то они и теоретически вычисляли частоту обращения ионов по кольцу, т.к. в работе [26] приводится длина кольца TSR 55,4 м, а в работе [41] ровно 55м. К тому же, они ничего не пишут как же они при этом определяли нужную напряженность магнитного поля на поворотах кольца, чтобы ионы двигались точно по радиусу закругления, если им при разгоне была неизвестна скорость пучка ионов. В общем, со скоростью пучка очень большой вопрос.

 

 

Да и вообще, сам ДОР это очень сложное явление, где при похожих условиях проведения эксперимента возможны различные варианты развития событий, которые можно ошибочно отождествить с нужным вариантом. К тому же, ионы лития у них облучались лучами лазеров в начале прямолинейного участка и в его конце, находясь в магнитном поле, и у нас тут могли вмешаться в полученный результат и магнитные резонансы и эффект Зеемана. Поэтому, я считаю, что при проведенных ими экспериментах, надо было не мудрить с ДОР, а просто фиксировать длину волны излучения при разных скоростях и углах наблюдения, а для возбуждения ионов использовать только один лазер. Ведь это только при излучении резонансная частота конкретной линии излучения строго определена, а поглощение может происходить в очень широком диапазоне частот вблизи этой резонансной частоты. К тому же, авторы экспериментов во всех статьях так и пишут, что они проводят эксперименты по типу Айвса и К. Вот и проводили бы их в этом духе, а у Айвса и К, так же, как и у Победоносцева и К, наблюдалась именно длина волны, испущенная ионами водорода. И им надо было наблюдать изменение длины волны излучения при разных скоростях пучка ионов и разных углах наблюдения, а не только при двух фиксированных углах, как это было у Айвса и К (примерно 7 и 173 градуса) и у Победоносцева и К (77  и 103 градуса).

 

 

К тому же у Айвса и К было большой проблемой, что соседние линии излучения водорода наползали на исследуемую им линию излучения иона водорода, а у них здесь будет только линия 548,5 нм, которая не только одна из самых ярких и расположена далеко от соседних линий (ближайшие 958,14 нм и 503,78 нм) но и возбуждение на этой длине волны у них в эксперименте осуществляется очень легко. А вообще-то, ионы надо было бы использовать в этом случае какой ни будь фракции со стабильным нижним уровнем, чтобы не приходилось через каждые 50 с впрыскивать в кольцо новую порцию ионов, т.к. время жизни электронов на метастабильном уровне 3S1, после которого электроны покидали этот уровень и без возбуждения, как раз и есть 50 с. А, если учесть, что для того, чтобы получить хорошую яркость линии излучения в спектроскопе, обычно требуется несколько часов, то эксперименты с метастабильным уровнем 3S1 станут очень затратными. К тому же, концентрация фракции ионов с метастабильным уровнем 3S1, после получения их на пеннинговском генераторе составляла у них всего 1% и то, как показал эксперимент на правом рис. 10, концентрация в этом случае была только 0,1% (такой вывод авторы сделали, наверное, по наблюдаемой интенсивности излучения). А в первых экспериментах концентрация таких ионнов в пучке была 10%, но здесь, как пишут авторы экспериментов, фракция метастабильных ионов была увеличена в процессе отгонки в ускорителе, но это  опять дополнительные затраты.

 

Таким образом, вот, когда германские ученые грамотно выполнят предлагаемые мною эксперименты со смещением известной линии излучения, а не с возбуждением неизвестно каких линий поглощения, то тогда их результаты будут интерпретироваться однозначно и можно будет что-то утверждать. А так авторы экспериментов провели кучу сложнейших экспериментов, научная ценность которых очень сомнительна, хотя они, не смотря на все их ошибки в методике проведения эксперимента, чего-то там и наблюдали. А вот как раз объяснить то, чего же там авторы этих экспериментов наблюдали, без дополнительной информации очень сложно (да и навряд-ли при наших познаниях о процессах поглощения и излучения вообще возможно сделать это однозначно), но давайте попробуем это сделать хотя бы в общих чертах, если справедлива классическая формула для эффекта Доплера. При этом будем считать, что некоторое отличие частот внешнего воздействия от резонансной частоты вполне допустимо, если мы рассматриваем именно резонанс, а не прыжки электронов с одного энергетического уровня на другой.

 

Ведь резонанс это растянутый во времени процесс, где амплитуда колебаний или возрастает (при возбуждении электрона) или убывает (при излучении, когда колебания затухают) со временем постепенно. И при этом круговые частоты этих колебаний электронов вдоль радиуса их орбиты определятся по формуле w=sqrt(kF/m), где kF это жесткость силовой функции на конкретной орбите. А еще есть режим близкий к резонансному, т.е. режим биений, когда частота внешнего воздействия может отличаться от собственной частоты колебаний электронов на 5 и более процентов, но мы и при биениях получим хорошую амплитуду возбуждения электронов на их резонансной частоте. При этом не надо забывать и о том, что резонанс может возникнуть и когда частота внешнего воздействия является одной из низших гармоник резонансной частоты, например, равна 1/2 или 1/4, а поэтому колебания с резонансной частотой могут возникнуть и при частоте внешнего воздействия меньше этой частоты. Таким образом, вполне возможно, что авторы этого эксперимента и наблюдали эффекты, которые  должны были происходить в этом эксперименте, но если справедлива классическая формула для эффекта Доплера. Например, если к частотам vp и va во втором эксперименте применить классическую формулу для эффекта Доплера, то мы получим одинаковые значения эффективных частот при скорости чуть-чуть больше 0,338*с, а именно при скорости 0,33836*с, (на рис. 14 это пересечение графиков эффективных частот лазеров (светло-зеленая и синяя линии) именно в точке 0,3384*с, которая найдена с точностью построения графиков).

 

 

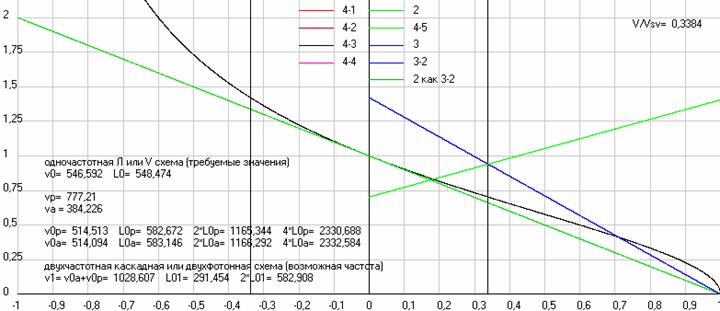
Рис. 14. Графики изменения нужной частоты лазеров в долях резонансной частоты излучения ионов в функции скорости пучка ионов рассчитанной по классическому эффекту Доплера (темно-зеленая прямая) и релятивистскому (черная кривая), а также графики изменения эффективных частот лазеров по классическому эффекту Доплера (светло-зеленая и синяя прямые) от заданных в экспериментах частот основного и сканирующего лазеров. Скриншот программы Dopler4.

 

 

А если скорость в эксперименте действительно была 0,338*с, а частоты лазеров с длиной волны 386 нм были vp=777,210 * 10^12 Гц и с длиной волны 780 нм va=384,226 * 10^12 Гц, то у нас при классическом эффекте Доплера получатся эффективные частоты 514,513*10^12 Гц и 514,094*10^12 Гц, которые вполне могли совпасть с частотами каких ни будь двух близких подуровней, т.к. от частоты v0=546,467 * 10^12 Гц эти частоты отличаются всего на 5,8%, что вполне позволяет возбудить даже эту частоту в режиме биений. А при наличии двухфотонного резонанса такой вариант даст излучение с частотой 1028,607*10^12 Гц, что, кстати, как раз и может объяснить пик на графике а) левого рис. 12 при одновременной работе лазеров.

 

 

Ну, а в первых экспериментах с двухуровневым ДОР, т.е. при скоростях 0,03*с и 0,064*с, у нас решение для заданных частот vp и va тоже будет единственным, когда их эффективные частоты совпадут, и получится оно тоже при почти этих скоростях (для 0,064 получится 0,06375). А при ровно 0,064 мы получим v01=545,482 * 10^12 Гц и  v02=545,211 * 10^12 Гц, что только на 0,2% отличается от резонансной частоты v0. Таким образом, и здесь вполне возможен резонанс в режиме биений, а если учесть то, что скорость пучка ионов в экспериментах подгонялась под резонанс с эффективной частотой одного из лазеров, то у нас тут обе эффективные частоты точно совпадут с частотой v0 и будет наблюдаться провал Лэмба. Да и образование темного провала тут тоже возможно, т.к. мощности лазеров были достаточные, а, судя по интенсивности излучения на рис. 9в, его образование даже более вероятно, чем образование провала Лэмба. В общем, вариантов развития событий в этих экспериментах очень много, поэтому не будем больше фантазировать, а дождемся, когда авторы выполнят свои эксперименты грамотно.

 

 

Таким образом, пока из рассмотренных нами экспериментов, без больших претензий к методике проведения эксперимента остается только эксперимент Победоносцева и К, который не подтверждает релятивистскую формулу эффекта Доплера (впрочем, как и классическую). При этом я опять говорю только о справедливости самой формулы, т.к. даже, если окажется, что подтверждается релятивистская формула, то это никоим образом не подтверждает именно эффекта замедления времени в движущихся объектах. Поэтому, сторонники СТО проводят и эксперименты по чистому поперечному эффекту Доплера, где, как они считают, должен наблюдаться именно эффект замедления времени и используют для этого эффект Мессбауэра, который был открыт в 1957 году. Суть этого эффекта состоит в том, что используется излучение и резонансное поглощение гамма-лучей ядрами в твердых телах без отдачи, т.е. без изменения импульса ядер. При обычных температурах частоты излучения и поглощения обычно не совпадают, а, как установил Мессбауэр, при низких температурах они совпадают, т.к. отдача не наблюдается. При этом, т.к. гамма-лучи имеют очень узкие линии излучения и поглощения и не перекрываются друг другом, то можно очень точно измерить даже незначительные смещения этих линий и это позволяет использовать гамма-излучение при изучении поперечного эффекта Доплера даже при нерелятивистских скоростях.

 

Обычно для этого используют высокоскоростные центрифуги, в которых источник излучения (чаще всего изотоп Co57) и поглотитель (чаще всего изотоп Fe57) помещают в разных частях этой центрифуги. Например,  источник помещают на оси ротора, а поглотитель на боковой стенке ротора. При этом сам ротор помещали в герметичный кожух, где создавали низкое давление, а в кожухе делалось окошко, сквозь которое не поглощенное гамма-излучение вылетало из центрифуги и регистрировалось счетчиком при пролете поглотителя мимо окошка. При этом в состоянии покоя регистрировалось максимальное поглощение, которое уменьшалось по мере раскрутки ротора. При такой конструкции радиальная скорость поглотителя относительно источника будет равна нулю, а тангенциальная скорость будет достаточной, чтобы дать такое замедление времени на поглотителе, которое можно будет зафиксировать по смещению линии поглощения гамма-излучения. Когда источник размещается точно над осью ротора, а поглотитель на его стенке, то мы должны получить смещение частоты поглощения dv в долях исходной частоты v согласно формуле (5), где V это линейная скорость поглотителя на боковой стенке ротора и b=V/c, а K=0,5. А, т.к. энергия гамма-кванта по Планку равна h*v, то точно таким же будет и смещение энергии.

 

dv/v = dE/E = V^2 / (2*c^2) = K*b^2                   (5)

 

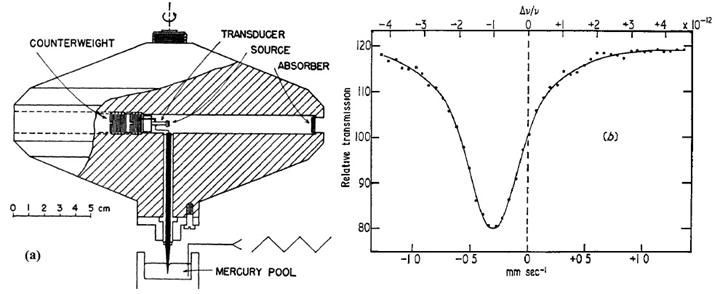
Рис. 15. a)- Схема центрифуги с источником излучения на оси ротора и поглотителем на его стенке (воспроизведено из работы [32]). b)- График интенсивности излучения прошедшего через поглотитель в функции радиальной скорости движения источника излучения, который находился на оси ротора, при подаче на вибратор через контакт в ртутной ванной пилообразного напряжения (воспроизведено из работы [29]).

 

Таким образом, чтобы после раскрутки ротора опять наступила максимальная интенсивность резонансного поглощения, нам надо каким то образом немного изменить частоту излучаемых волн или, как принято говорить, гамма-квантов. Для этого используются различные вибраторы (обычно пьезоэлектрические преобразователи), которые при подаче на них пилообразного напряжения заставляют источник перемещаться с очень маленькой линейной скоростью (меньше миллиметра в секунду) в радиальном направлении, то сближаясь с поглотителем, то удаляясь от него. При этом возникает продольный эффект Доплера, величину которого легко определить по радиальной скорости, и за счет этого изменяется частота излучателя. Вот таким образом, постепенно изменяя радиальную скорость излучателя, определяют смещение линии поглощения по частоте, когда опять наступает максимальное поглощение излучения.

 

И первые такие эксперименты, которые подтвердили релятивистское замедление времени по красному смещению линии поглощения, провел Хэй уже в 1960 году. Затем их повторили в 1961-1965 годах Кёнинг [32] и Чемпни и К [28, 29]. Но до настоящего времени самыми точными (с технической точки зрения) считались эксперименты Кёнинга, которые с точностью до 1,1% доказывали в этих экспериментах наличие красного смещения, т.е. замедление времени на поглотителе, которое и привело к смещению линии поглощения в красную сторону. Вот только не менее точные эксперименты выполненные в 2008-2010 годах Холмецким и К [35, 36] доказывают, что в формуле (5) коэффициент K должен быть равен 0,6. При этом, как они пишут, и если экспериментальные данные Кёнинга обработать грамотно с помощью метода наименьших квадратов, то мы тоже получим K=0,6. Таким образом, расхождения сейчас заключаются только в величине коэффициента, но то, что здесь будет квадратичная аппроксимация экспериментальных данных, расхождений нет.

 

При этом если мы будем формально рассматривать в этом эксперименте чисто кинематические эффекты СТО, то у нас получится смещение частоты принимаемых сигналов, не в красную, а в синюю сторону. Здесь поглотитель (приемник) будет двигаться перпендикулярно лучу зрения, т.е. мы будем наблюдать только поперечный эффект Доплера согласно формуле (4-1), где у нас остается только релятивистский множитель в знаменателе, т.к. cos(Q12)=0. Теперь, пусть эталонный передатчик, покоясь в абсолютной системе отсчета (АСО), т.е. при эталонном темпе течения времени, генерирует сигналы с частотой 1 Гц. В наличие такого эталонного времени, в принципе, нет ничего крамольного с точки зрения теории относительности, т.к., например, в ОТО замедление времени определяется относительно темпа течения времени вдали от гравитирующих масс, т.е. за эталонное значение принимается темп течения времени, когда полностью отсутствует этот эффект (та же АСО). Вот пусть и у нас источник покоится в АСО, а приемник движется со скоростью 0,866*с, т.е. sqrt(1-b^2)=0,5, и у нас получается так.

 

 

Передатчик за 10 эталонных секунд и сделает 10 колебаний, но, т.к. темп течения времени на приемнике будет в 2 раза меньше темпа течения эталонного времени, то мы на абстрактном приемнике зарегистрируем эти 10 колебаний за 5 секунд и получится, что частота принимаемых сигналов увеличится в 2 раза, т.е. сдвинется в синюю сторону, что соответствует формуле (4-1). А, т.к. нам надо, чтобы излучение было поглощено, т.е. чтобы частота на приемнике получилась равной v0, то нам надо частоту источника уменьшить, т.е. сместить в красную сторону. Но, т.к. частота покоящегося источника никак не могла измениться в эксперименте, то отсюда делается вывод, что это резонансная частота поглотителя сместилась в красную сторону. Таким образом, результат в этом эксперименте полностью соответствует релятивистской формуле для эффекта Доплера. И, если мы рассмотрим этот эксперимент с чисто физической точки зрения реального замедления времени в движущемся поглотителе, то и в этом случае у нас результат будет соответствовать этому следствию из СТО. Ведь в этом случае у нас и все физические процессы должны проходить в системе поглотителя в замедленном темпе течения времени, т.е. и все колебания в атомах поглотителя должны проходить с частотой, которая будет меньше, чем в системе, где время не замедлялось. Следовательно, резонансная частота поглощения атомов уменьшится, и линия поглощения сдвинется в красную сторону, т.е. вроде как получается полный триумф СТО.

 

А, вообще-то, данный эксперимент, где поглотитель движется с центробежным ускорением, не соответствует принципам СТО, где рассматриваются только инерциальные системы, т.е. движущиеся без ускорения и поэтому по результатам этого эксперимента нельзя доказывать справедливость СТО. Но авторы этих экспериментов считают, что у них тут СТО можно применять (наверное, потому что в первом эксперименте все хорошо сошлось с ответом по СТО). А в соответствии с правилами теории относительности (ТО), т.к. тут рассматривается движение в неинерциальной системе, то надо применять ОТО, где движение с постоянным ускорением эквивалентно движению в гравитационном поле, если на ускоряемое тело действует та же сила, что и в гравитационном поле. Таким образом, движение изотопов с постоянным центробежным ускорением можно приравнять к их движению в гравитационном поле, приводящему к такому же замедлению темпа течения времени. Кстати, именно такой эксперимент при движение гамма-квантов в гравитационном поле и был первым с использованием эффекта Мессбауэра. Его выполнили Паунд и К [33, 34], которые в первых экспериментах помещали излучатель на башне высотой H=22,5 м, а поглотитель со счетчиком помещали у основания башни. При движении гамма-кванта в гравитационном поле он падая вниз получает дополнительную скорость и, следовательно, увеличивается его кинетическая энергия, а отсюда, т.к. E=h*v, и частота. Таким образом, относительное увеличение частоты при движении гамма-кванта с постоянным ускорением g будет

 

dv/v = dE/E = g*H / c^2           (6)

 

В эксперименте они получили значение dv/v с точностью до 4% согласующееся с расчетным значением dv/v= 2,45*10^-15, но далось это им нелегко, т.к. первоначально у них на семи дисках поглотителей получались результаты от 8*10^-15 до 30*10^-15. Как пишут авторы, это было связано с разностью температур у излучателя и дисков поглотителя, а различие в 1 градус дает погрешность 2,44*10^-15, т.е. столько же, сколько и сам эффект. И только после учета этой поправки они получили нужный результат, который подтвердили в последующих экспериментах, где они помещали и излучатель внизу, а поглотитель наверху, и при этом уже помещали их в термостаты. Здесь при перемене местами излучателя и поглотителя смещение получается одно и тоже, но с другим знаком. Вот только у меня возникает множество, как чисто технических, так и теоретических вопросов по этому эксперименту.

 

 

Во-первых, не понятно как в первых экспериментах у семи поглотителей, которые были расположены рядом, могла оказаться разной температура на целых 9 градусов, т.к. (30-8)/2,44=9,01. Быстрее всего, это какие то другие неучтенные погрешности в эксперименте. Да и вообще, в этом эксперименте все на грани фола. Например, чтобы спектральная линия изотопа Fe57 с энергией 14,4 кэВ сместилась, хотя бы, на свою ширину, нужна разность по высоте излучателя и поглотителя более 3000 м, а мы имеем только 22,5 м. Поэтому, здесь бы надо было использовать изотоп Zn67 у которого отношение ширины линии к энергии гамма-кванта будет 5,2*10^-16, а у изотопа Fe57 это отношение равно 3,1*10^-13, т.е. на три порядка больше. И многие экспериментаторы, например у нас в Дубне и в Америке в Лос-Аламоссе, так же, как и Паунд и К в Гарварде в начале своего исследования, проводили подобный эксперимент именно с изотопом Zn67, но что то у них у всех дружно не заладилось с изотопом Zn67. Ладно, оставим на совести этих граждан полученные ими результаты и будем отталкиваться оттого, что они достоверные и подтверждают наличие гравитационного красного смещения.

 

 

Вот только этот эффект изменения частоты излучения имеет не только квантовое объяснение из-за потерянной или приобретенной гамма-квантом энергии при движении в гравитационном поле, но и объяснение исходя из эффекта замедления темпа течения времени в гравитационном поле согласно ОТО. И Паунд и К упоминают в своей статье об этом варианте, как об эквивалентном рассмотренному ими и где уже время будет протекать на источнике и поглотителе с различным темпом и это даст относительное увеличение частоты излучения на величину g*H / c^2. Причем, эти два варианта объяснения считаются сейчас равнозначными (наверное, потому, что результат получается один и тот же), но ведь это два совершенно разных физических эффекта. И, если оба эти объяснения верны, то учитывать надо оба этих эффекта, т.е. результат у Паунда и К должен был получиться в два раза больше. Кстати, они в своих теоретических расчетах все таки учитывали и эффект от замедления времени, когда рассчитывали температурную поправку, т.к. там в расчете используется среднеквадратичная скорость колебания атомов, которая приводит согласно СТО к скоростному замедлению времени, но вот учесть в своем эксперименте и гравитационное замедление времени согласно ОТО не пожелали.

 

 

Правда, сейчас в академических изданиях, наконец-то, наметилась некоторая дискуссия по этому вопросу и начинают утверждать, что верно только объяснение гравитационного красного смещения согласно ОТО. А вот автор [9], анализируя эту дискуссию, утверждает, что эти объяснения согласно ТО противоречат друг другу, т.е. получается, что пока еще сами сторонники ТО не знают этой самой ТО. К тому же, например, в работе [30] наоборот показывается, что не только результат полученный Паундом и К, но и многие результаты, которые объясняются в рамках ОТО за счет замедления времени, можно объяснить только изменением скорости света в гравитационном поле и, следовательно, не нужно никакое замедление времени по ОТО. Таким образом, мы видим, что пока нет единого мнения по вопросу о том, что же доказывают эксперименты Паунда и К. Тем более, не понятно надо ли учитывать и гравитационное замедление времени в экспериментах с центрифугами, а поэтому мы опять тут видим два равнозначных объяснения получающихся результатов по замедлению времени: или согласно СТО или согласно ОТО. А, т.к. и в этих экспериментах оба применяющихся теоретических расчета дают один и тот же результат (5), то различные авторы в зависимости от того, какое объяснение больше подходит, выбирают или одно объяснение или другое.

 

 

А в работе [38] автор даже приводит формулу (10-210) для суммарного эффекта по частоте сигнала, принимаемого приемником в центре окружности от источника движущегося по окружности с релятивистской скоростью в гравитационном поле, который будет равен произведению результата по релятивистской формуле Доплера, т.е. с учетом замедления времени согласно СТО, и результата от замедления времени по ОТО. Но далее он тоже дает пояснения, что для наблюдателя находящегося в центре вращения, т.е. в Лоренцевской системе координат, будет замедление времени по СТО, а для наблюдателя находящегося во вращающейся системе координат, т.е. в Эйнштейновской системе координат, замедление времени будет по ОТО, но при этом результат с математической точки зрения будет один и тот же. Таким образом, получается, что, т.к. у нас в экспериментах с центрифугами положение наблюдателя, коим является поглотитель, который и наблюдает частоту резонансного поглощения, всегда строго определено, то у нас и не должно быть проблем с выбором одного из двух объяснений этого эффекта.

 

 

 

 

Вот только когда сторонники ТО рассматривают эксперименты не связанные с центрифугами, то об этих скачках из одной системы в другую и выбора при этом или СТО или ОТО как-то забывают и рассматривают в Лоренцевой системе оба эффекта. Так, например, в принципе наименьшего действия в релятивистской форме учитывается, как гравитационное замедление времени ОТО, так и скоростное замедление времени СТО (причем они тут суммируются). А конкретно этот принцип в релятивистской форме говорит о том, что на действительном пути замедление времени от гравитации и скорости движения будет минимальным. Правда, я проверил это утверждение экспериментально [13] на примере, который приводил Фейнман, с полетом ракеты в поле тяжести Земли, и увидел, что в Природе этот принцип не наблюдается, но сторонники ТО этого знать не желают и, следовательно, когда это им нужно используют этот принцип, где разрешают времени замедляться по двум теориям сразу.

 

 

И при рассмотрении, например, частоты импульсов приходящих от двойных пульсаров, т.е. от нейтронных звезд, которые и посылают эти импульсы, и при этом еще и с большой скоростью вращаются вокруг других нейтронных звезд, сторонник ТО учитывают при этом и замедление времени согласно ОТО и замедление времени согласно СТО (причем опять суммируют, а не умножают, как рекомендовано [38]). Смотрите, например, Нобелевскую лекцию [4] по двойному пульсару PSR 1913+16. Вот только авторы экспериментов с центрифугами почему-то отказываются учитывать оба замедления времени. Я так догадываюсь, что это потому, что у них в этом случае по их формулам результат будет получаться в два раза больше наблюдаемого (так же, как и в эксперименте Паунда и К).

 

А вообще то, в этих экспериментах мы имеем движения в неинерциальных системах и получается, что применимы тут только принципы ОТО, но давайте пока закроем на это глаза и попробуем объяснить результаты экспериментов по рекомендациям [38]. Таким образом, полученные результаты будем рассматривать с позиции СТО, когда наблюдатель не движется или с позиции ОТО, если он движется по круговой орбите, т.е. мы пока не будем учитывать одновременно замедление времени и по СТО и по ОТО. Таким образом, будем анализировать экспериментальные данные, полученные на центрифугах, с точки зрения подтверждения их релятивистской формулой эффекта Доплера, только те, для которых СТО применима с этой точки зрения. И так, мы имеем три варианта экспериментов, когда излучатель и поглотитель помещались в разных местах ротора и имеем три разных результата, когда у нас было смещение частоты линии поглощения от частоты излучения в красную сторону -1, синюю +1 и отсутствовало 0.

 

При этом давайте договоримся, где у нас будет красное смещение, а где синее, т.к. одни авторы рассматривают изменение частоты излучения v, а другие частоты поглощения vp. Например, Чемпни и К кругом пишут, что в первом варианте у нас частота излучения смещается в синюю сторону от обычного состояния, когда и излучатель и поглотитель не движутся, а во втором варианте в красную. Но я считаю, что, т.к. мы регистрируем приборами именно частоту поглощения, то корректно говорить об отклонении именно этой частоты от частоты излучения, т.к. наблюдателем на приемнике у нас был именно поглотитель. В первом варианте, чтобы наступило резонансное поглощение, задавали вибратором отрицательную линейную скорость излучателя (см. рис. 15б), т.е. уменьшали частоту излучения и, следовательно, частота поглотителя была смещена в красную сторону. Во втором варианте задавали наоборот положительную скорость, т.е. увеличивали частоту излучения, чтобы она совпала с частотой поглощения, т.е. частота поглотителя была смещена в синюю сторону. Ну, а в третьем варианте ничего не делали, т.к. частота излучения и так совпала с частотой поглощения.

 

1.- источник-ось ротора                 ---->     поглотитель-стенка            -1        ОТО=-1    СТО=-1

2.- источник- стенка ротора     ---->     поглотитель- ось ротора         +1        СТО=+1    СТО=+1

3.- источник- стенка ротора     ---->     поглотитель-стенка ротора       0        ОТО=0     СТО=-4

 

Вариант 1. Мы имеем наблюдателя в движущейся с ускорением системе и, следовательно, должны применить ОТО, где излучатель в этой системе координат будет покоиться и его потенциал будет равен нулю, а поглотитель будет иметь отрицательный потенциал и у него будет замедление времени. Таким образом, все процессы в поглотителе будут проходить в замедленном темпе и частота поглощения vp сместится в красную область, т.к. будет меньше v= v0. А, чтобы она совпала с частотой излучения, последнюю надо уменьшить и нам надо задать излучателю отрицательную скорость, что и мы и делали, т.е. объяснение соответствует наблюдаемым результатам.

Вариант 2. У нас наблюдатель находится в неподвижной системе и, следовательно, мы должны (вернее, можем) применить СТО. Тут время замедлится на излучателе и частота излучения v станет меньше v0, а частота поглощения vp=v0 получится больше v, поэтому, чтобы они совпали, надо будет увеличивать частоту излучения и задавать положительную скорость сближения излучателя и поглотителя, что в экспериментах и делалось. Таким образом, и здесь теория объясняет результат.

Вариант 3. Мы имеем опять наблюдателя в движущейся с ускорением системе, т.е. должны применить ОТО. Здесь время должно замедлиться и на источнике и на поглотителе, т.к. они оба имеют отрицательный потенциал относительно оси ротора и у нас будет и v<v0 и vp<v0, т.е. не будет никакого смещения резонансной частоты поглощения, что и наблюдалось.

 

Таким образом (смотрите предпоследнюю колонку в списке вариантов), ТО объясняет все варианты экспериментов, но два с точки зрения ОТО, и при этом сторонники ТО иногда еще говорят, что и во втором варианте мы имеем дело с движением в неинерциальной системе координат (и ведь правильно говорят) и поэтому для объяснения полученного результата надо использовать не СТО, а тоже ОТО, т.е. рассматривать результат с точки зрения наблюдателя движущегося с ускорением. Но это уже, как говориться, перебор, т.к. мы рассматриваем полученные в экспериментах результаты с точки зрения наблюдателя, а им в этих экспериментах был поглотитель, а не излучатель. И потом, если мы и второй вариант рассмотрим с точки зрения ОТО, то какое отношение ко всем этим экспериментам будет иметь СТО, с помощью которой сторонники ТО и пытаются доказать справедливость релятивистской формулы для эффекта Доплера и как следствие скоростное замедление времени.

 

А теперь давайте рассмотрим более внимательно вопрос о гравитационном замедлении времени по ОТО на боковой стенке ротора. Обычно при рассмотрении этого вопроса берут потенциал поглотителя при его вращении такой, как будто бы он вращается не жестко прикрепленный к стенке ротора, а в гравитационном поле, и удерживается на этой орбите, равной радиусу ротора, именно силами этого поля. А в результате получают результат такой же, как и согласно скоростному замедлению времени в СТО, т.е. в соответствии с уравнением (5). Позвольте, но я что-то не понимаю - какая может быть потенциальная энергия у поглотителя жестко прикрепленного к боковой стенке ротора. Вот у спутника, вращающегося вокруг Земли в ее гравитационном поле, есть потенциальная энергия, а у поглотителя ее нет, если не считать его энергии в поле тяготения Земли, но она не изменяется при раскрутке ротора. Или в эксперименте Паунда и К гамма-кванты движутся в потенциальном поле и за счет этого изменяют свою скорость, а у нас поглотитель и излучатель движутся строго горизонтально и не меняют своей скорости от движения в потенциальном поле Земли.

 

 

Поэтому, формула дающая при таком потенциале замедления времени по ОТО такое же, как и по СТО, является явно ошибочной и нам надо здесь рассматривать замедление времени по ОТО в полном согласии с ОТО, т.е. с движением именно в гравитационном поле ротора а, следовательно, учесть его гравитационный радиус Rg. Таким образом, согласно расчету одного из участников дискуссии [31], для наших экспериментов с центрифугой мы получим dv/v согласно СТО порядка 10^-12, что мы и наблюдаем, а согласно ОТО порядка 10^-26. Здесь в расчете принято: масса ротора 1 кг, радиус R=0,1 м, угловая скорость w=6000 рад/с. Таким образом, замедление времени по ОТО в наших экспериментах можно вообще не учитывать. Но и этот расчет я считаю все-таки не совсем корректным, т.к. опять таки мы привязываемся к потенциалу поля, в котором движется поглотитель на краю ротора. Более корректным здесь будет учесть замедление времени по ОТО, как движение в поле, дающем такое же ускорение, как и в наших экспериментах, где поглотитель движется по окружности с постоянным центробежным ускорением.

 

 

При расчете гравитационного красного смещения согласно ОТО у нас частота поглощения изотопов v или длина волны L в гравитационном поле будут определяться по нижеприведенным зависимостям, где Zg - относительное смещение спектральных линий под влиянием гравитации.

 

v=v0 / (1+Zg)                                  (7-1)

L=L0*(1+Zg)                                  (7-2)

Zg= G * M / (R*c^2)                         (8)

 

Здесь G - гравитационная постоянная, M - масса гравитирующего тела, R - расстояние от центра массы M, c - скорость света. Для Земли Zg будет 6,95 * 10^-8, что равнозначно движению с ускорением свободного падения 9,8 м/с^2, а центробежное ускорение, которое будет действовать на поглотитель в эксперименте Кёнинга при радиусе центрифуги R=0,093 м и при одной из угловых скоростей, что были в эксперименте, w=31000 об/мин (3246 рад/с), будет a=R*w^2 = 9,8*10^5 м/с^2, т.е. в 100000 раз больше, чем на поверхности Земли. Следовательно, скоростное красное смещение Za= Zg*a/9,8= 6,95*10^-3. Таким образом, у нас теперь получается смещение линии поглощения от замедления времени по ОТО наоборот на много порядков больше, чем смещение от замедления времени по СТО, что нас явно не устраивает. Более того, такой подход к расчету замедления времени по ОТО и напрямую противоречит экспериментальным данным приведенным в таблице 2 [36], где видно, что при разных диаметрах центрифуг, но при примерно одинаковых данных по линейным скоростям у Чемпни и К, Кёнинга и Холмецкого и К ускорения будут отличаться более чем на порядок. Но результаты по смещению резонансной линии у них получились одинаковыми и, следовательно, ускорение не оказало на них никакого влияния.

 

Таким образом, эффект от гравитационного замедления времени по ОТО никак не может быть использован для объяснения результатов получающихся в экспериментах по смещению линий поглощения у изотопов в мессбауэровских центрифугах, т.е. объяснения вариантов 1 и 3 по ОТО отпадают. Но давайте тогда, учитывая настойчивые просьбы сторонников СТО, попробуем и их объяснить в рамках СТО (последняя колонка в списке вариантов). Что касается 1-го варианта, то здесь можно сказать, что на движущемся относительно излучателя поглотителе замедлилось время и уменьшилась частота поглощения, ставшая меньше частоты излучения, которая не изменялась, т.е. так мы можем объяснить результат этого эксперимента. А вот с объяснением 3-го варианта экспериментов по СТО получается  парадоксальный результат, которому удивились и сами авторы этого эксперимента [28]. Ведь, как пишут Чемпни и К, мы имеем здесь скорость источника излучения относительно поглотителя (наблюдателя) 2*V, т.е. согласно формуле (5) должно было получиться смещение в красную сторону в четыре раза больше, чем в варианте 1, а его вообще нет.

 

И тут сторонники СТО начинают придумывать различные варианты, прибегая к своим прыгающим из одной системы в другую наблюдателям. Одни заявляют, что этот эксперимент надо рассматривать с точки зрения наблюдателя, находящегося на оси ротора. Тогда замедление времени будет и у излучателя и у поглотителя, а, следовательно, будет нулевой результат в смещении частоты поглощения. Но и здесь придется сделать замечание о том, что этот наблюдатель не имеет никакого отношения к третьему варианту наших экспериментов, где наблюдатель, т.е. поглотитель, находился на краю ротора. Другие заявляют, что этот вариант надо рассматривать во вращающейся системе поглотителя, т.е. в Эйнштейновой системе, но замедление времени считать по скоростям, как в Лоренцевой системе. Тогда скорость источника относительно поглотителя будет равна нулю, и получим нужный результат. Ара! Получилось. Не знаю, как Вам, а мне разнообразные варианты объяснения сторонников ТО экспериментов с центрифугами напоминают гадание на кофейной гуще и их устраивает даже решение, в котором нарушаются все требования ТО, если при этом получается результат, который совпадает с ответом в конце задачника. Но давайте придерживаться хоть каких ни будь правил ТО при объяснении результатов с центрифугами.

 

А согласно этим правилам мы выяснили, что ОТО хоть и применима в вариантах 1 и 3, но она дает значения смещений на много порядков меньше, чем наши наблюдаемые значения, поэтому ее можно вообще не учитывать в расчетах. Для варианта 2 мы, согласно рекомендациям учебника, можем применить СТО и она даст нужный результат, но вообще то, применение СТО и для этого варианта некорректно, т.к. по сути движение излучателя происходит в не инерциальной системе. А вот как быть с вариантами 1 и 3 вообще не понятно, т.к. СТО здесь применять дважды нельзя, а ОТО дает очень незначительный эффект. Таким образом, ТО не может объяснить всех вариантов наших экспериментов, а, следовательно, не объясняет ничего. Но, не смотря на это сторонники ТО продолжают давать интерпретацию результатов этих экспериментов, и применяя СТО там, где ее нельзя применять, и применяя в неверной трактовке расчеты по ОТО.

 

А вот Чемпни и К решили все же объяснить результаты всех трех вариантов в рамках СТО и для этого они решили применить формулу (4-6), где используют не относительную скорость поглотителя относительно источника излучения V12, а абсолютные скорости - V1 для поглотителя и V2 для источника излучения. При этом, как я писал, Чемпни и К говорят об увеличении частоты излучения при движущемся приемнике (это соответствует формуле (4-1), т.е. Эйнштейна) и об уменьшении частоты при движущемся источнике (это соответствует формуле (4-2), т.е. Ландау). Эта их формула (4-6) легко получается из формулы Айвса (4-5), если убрать радиальные скорости, которые будут равны нулю. Таким образом они тоже, как и Айвс, рекомендуют рассматривать эффект Доплера в абсолютной системе отсчета, где в зависимости от того, что покоится надо использовать или формулу (4-1) или формулу (4-2) или сразу обе формулы, если движутся и источник и поглотитель.

 

v =v0* sqrt(1 – b2^2) / sqrt(1 – b1^2)                       (4-6)

 

Да, если теперь рассматривать результаты экспериментов по формуле (4-6) в трактовке Чемпни и К, то она их теперь объясняет, но теперь это уже дважды не СТО, т.к. и здесь у нас опять используются абсолютные скорости, а не относительные, т.е. мы определяем, что покоится, а что движется, и это не считая того, что у нас движение по кругу никак не соответствует движению в ИСО. Таким образом, и здесь мы видим у Чемпни и К, которые являются сторонниками ТО, неудовлетворенность существующими формулами (4-1) и (4-2) или (4-3), которые дают идентичный результат для продольного эффекта Доплера, но при поперечном эффекте дают совершенно противоположные результаты, и они пытаются подправить СТО, чтобы она могла объяснить результаты их экспериментов, но при этом нарушают ее же принципы. Итого, ни СТО ни ОТО объяснить результаты экспериментов с центрифугами не могут, поэтому давайте попробуем их объяснить в рамках классической механики. На рис. 16 Вы видите поглотитель и излучатель, которые закреплены на краю ротора, т.е. движутся с линейной скоростью V.

 

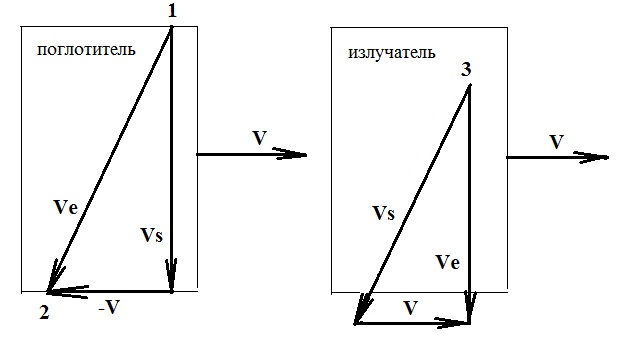
Рис. 16. Схема сложения скоростей для расчета суммарной скорости излучения при движущемся поглотителе (слева) и при движущемся излучателе (справа).

 

Излучение со скоростью Vs входит в поглотитель в точке 1 и проходит его за время dt, а поглотитель за это время немного смещается вправо и в результате излучение выходит из поглотителя в точке 2, т.е. проходит в поглотителе путь больше чем толщина поглотителя. А, т.к. за то же самое время dt излучение пройдет больший путь, то это будет эквивалентно тому, что у нас увеличилась скорость воздействия на атомы поглотителя (приемника) а, следовательно, и частота этого воздействия. Если мы теперь определим по формуле (9) эту суммарную скорость излучения Ve, то по формуле (10) мы можем рассчитать относительное смещение эффективной частоты излучения относительно стандартной частоты излучения. А по формуле (10-1) мы можем рассчитать относительное смещение частоты поглощения движущегося поглотителя относительно частоты излучения покоящегося излучателя, т.е. рассматривая этот процесс с точки зрения наблюдателя, которым в рассмотренных нами экспериментах был поглотитель. Естественно, сама частота поглощения при этом не меняется, но при рассмотрении экспериментов с центрифугами с точки зрения теории относительности мы вынуждены были рассматривать изменение именно ее.

 

Ve= sqrt(Vs^2+V1^2)                      (9)

dv/v= (Ve - Vs) / Vs                        (10)

dv/v= (Vs - Ve) / Vs                       (10-1)

Ve= sqrt(Vs^2-V2^2)                       (11)

 

Аналогичный процесс изменения скорости излучения мы будем наблюдать и при выходе излучения из ядра атома в точке 3. Чтобы излучение со скоростью Ve у нас пошло строго по отверстию в роторе, т.е. перпендикулярно плоскости излучателя, оно должно вылететь в направлении скорости Vs. По правилам классической механики суммарная скорость излучения Ve определится согласно формуле (11), как сумма скоростей Vs и V2, а относительное смещение эффективной частоты излучения опять определим по формуле (10). А для покоящегося поглотителя это смещение его частоты поглощения относительно частоты излучения движущегося излучателя опять определим по формуле (10-1). В общем-то, тут более корректно все время говорить об изменении именно эффективной частоты самого излучения, т.е. всегда использовать формулу (10), но, т.к. мы все эксперименты рассматривали с точки зрения наблюдателя, которым был поглотитель, то приходится обращаться и к формуле (10-1). А в дальнейшем я буду говорить только об изменении эффективной частоты излучения и поэтому буду использовать только формулу (10).

 

Если мы теперь по этим формулам построим графики изменения частоты излучения или поглощения относительно стандартной частоты излучения или поглощения для рассмотренных выше вариантов 1 и 2 в функции линейной скорости края центрифуги, то мы получим две параболы, как показано на рис. 17. Верхняя парабола отражает увеличение эффективной частоты излучения относительно стандартной частоты излучения (при движении поглотителя излучения), а нижняя уменьшение частоты излучения источника излучения относительно стандартной частоты излучения (при движении источника излучения). Если мы теперь построим точно такие же графики при движении поглотителя и излучателя по формуле (5), то мы получим точно такие же параболы, которые совпадут с нашими параболами (если перед формулой (5) поставить знаки плюс и минус. Т.е. численно мы по формуле (10) получим точно такой же результат, как и по формуле (5) и смещения в красную и синюю стороны у нас тоже будут соответствовать экспериментальным данным.

 

 

Рис. 17. Графики изменения эффективной частоты излучения (в долях стандартной частоты) в функции от скорости центрифуги, построенные по формулам (5) и (10) для движущегося на краю ротора поглотителя излучения - верхняя парабола и источника излучения - нижняя парабола (графики по формулам (5) и (10) совпали). Скриншот программы Dopler4.

 

Таким образом, если наблюдаемые смещения частоты в экспериментах соответствуют формуле (5), то все эксперименты в вариантах 1, 2 и 3 с центрифугами, отлично объясняются в рамках классической механики, когда мы используем классическую формулу для эффекта Доплера не имеющую поперечного эффекта, а изменения частоты поглощения или излучения объясняем обычным эффектом звездной аберрации при классическом сложении скоростей. Но из этого не следует вывод, что релятивистские формулы своим релятивистским членом отражают именно эффект аберрационного смещения частоты излучения или поглощения, т.к. при продольном эффекте Доплера никакого аберрационного смещения частоты не будет, а релятивистские формулы будут давать его наличие (и очень, очень большое). Следовательно, релятивистский член отражает именно замедление времени, которое заметно влияет на общий результат даже в том случае, когда аберрационных эффектов, т.е. происходящих именно в источнике или приемнике, нет или они не значительные. Но при очень маленьких скоростях, которые были у центрифуг, этот релятивистский член очень удачно отражает аберрационные эффекты, хотя при скоростях примерно больше 0,5*Vs расхождения в данных рассчитанных по формулам (5) и (10) станут уже заметными (см. рис. 18).

 

 

 

 

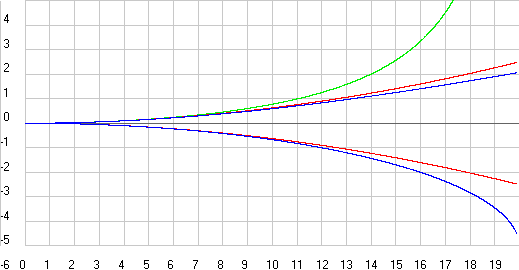
Рис. 18. Графики изменения эффективной частоты излучения (в долях стандартной частоты) в функции от скорости центрифуги, построенные по формулам (5) - красные кривые и (10) - синие кривые для движущегося на краю ротора поглотителя излучения (верхние параболы) и источника излучения (нижние параболы). Зеленые параболы точный расчет по формулам (4-1) - верхняя парабола и (4-3) - нижняя парабола, которая совпала с расчетом по формуле (10). Максимальное значение скорости равно Vs, а максимальное смещение частоты dv/v равно +/-1. Скриншот программы Dopler4.

 

При этом приблизительной формулой (5), согласно математическим справочникам, можно пользоваться при значении b1=V1/Vs только до 0,052, а при b2=V2/Vs только до 0,085, что нас вполне устраивало, когда мы рассматривали эксперименты с центрифугами, но вот в других экспериментах, где скорость приемника или источника будет больше, надо использовать уже точный расчет смещения частоты с использованием непосредственно формул (4-1) и (4-3). В этом случае смещение будет рассчитываться уже не по формуле (5), а по формулам (5-1) и (5-2).  А, если произвести расчеты по этим точным формулам, то здесь у нас (см. зеленые кривые на рис. 18) при движении источника результат точно совпадет с классическим расчетом, а при движении приемника будут очень большие расхождения. Таким образом, релятивистский член в релятивистских формулах не отражает и численно аберрационные поправки даже при чистом поперечном эффекте Доплера, хотя при малых скоростях и получаются одинаковые результаты.

 

dv1/v= 1 / sqrt(1-b1^2) - 1                                    (5-1)

dv2/v= sqrt(1-b2^2) - 1                                         (5-2)

 

 

Только не надо отождествлять суммарную (эффекивную) скорость излучения на приемнике или на источнике со скоростью передачи сигнала между источником и приемником. Например, и чисто продольный эффект Доплера можно точно так же описать в терминах суммарной скорости излучения, где сама скорость распространения сигнала остается неизменной. Для приемника будет Ve1= Vs-V1, а для источника Ve2= Vs+V2, и тогда формула для продольного эффекта Доплера запишется как (3-1). Как видим, у нас получилась не совсем формула (3), где вместо умножить на 1+b2 стоит разделить на 1-b2, т.е. эта формула будет справедлива только при движении приемника. И хотя, при малых скоростях, когда b2<0,031, и общий результат будет примерно одинаковый и по формуле (3) и по формуле (3-1), но нам нужна точная формула, а получить ее часто аналитически через эффективные скорости пока не получается даже для продольного эффекта. Поэтому, для общего эффекта надо или создавать математическую модель, учитывающую и возникающие аберрационные эффекты, или попробовать учесть их в математическом имитаторе (3) как то по-другому. Ведь аберрационные эффекты отражают только изменение частоты в самих источнике и приемнике, а изменение частоты в пространстве между источником и приемником должно отражаться уже обычной формулой для эффекта Доплера и, следовательно, суммарные (эффекивные) скорости должны использоваться только в расчете аберрационных поправок. Таким образом, я сейчас просто вынужден, как говорят юристы "в связи со вновь открывшимися обстоятельствами", как-то подправить свою формулу (3), чтобы она отражала аберрационные поправки.

 

 

v= v0*Ve1*Ve2 / Vs^2= v0*(1-b1)*(1+b2)                                                                    (3-1)

 

 

Вообще-то, я примерно последние лет 10 периодически задумывался о том, как может отразиться эффект звездной аберрации на показаниях радиотелескопов, т.к. постоянно приходилось работать с данными астрономических наблюдений, где учитываются различные поправки. И, например, эффект планетной аберрации, который обусловлен движением источника света, я давно учел в формуле эффекта Доплера, как запаздывание сигнала по координатам. Вернее, я его сначала учел при определении силы Fn(i,k) в формуле (1), т.к. и занимался и сейчас занимаюсь именно вопросом определения скорости гравитации, а поэтому рассматриваю все эффекты, которые могут быть именно при гравитационном взаимодействии между телами. А вот эффект звездной аберрации, который обусловлен движением приемника света, и который отлично объясняется для телескопов, я не только не знал как учесть в силе гравитационного взаимодействия или в показаниях радиотелескопов но, до рассмотрения экспериментов с мессбауэровским центрифугами, у меня не было даже доказательств того, что этот эффект должен присутствовать и в эффекте Доплера.

 

 

Сейчас я знаю, что этот эффект надо учитывать, но вот привести окончательную формулу имитатора для общего эффекта Доплера я затрудняюсь, т.к. у меня у самого пока еще физическое объяснение воздействия суммарных скоростей не вызывает никаких вопросов только при воздействии этой скорости на поглотитель. Могу только, как предварительный вариант предложить формулы двух имитаторов (3-2-1) и (3-2-2), которые включают в себя формулу (3) к которой добавляются два аберрационных эффекта от источника со скоростью V2 и приемника со скоростью V1. При этом аберрационные поправки будут рассчитаны по приблизительным формулам (3-2-11) и (3-2-12), где эффективные скорости Ve1 и Ve2 будут рассчитаны по формулам (9) и (11). Графики изменения принимаемой частоты для движущегося источника, рассчитанные по формуле (3-2-1) и по формуле (2) с аберрационными поправками (3-2-1), приведен на рис. 19. Сейчас я считаю формулу (3-2-2) более корректной, чем (3-2-1), но с доказательствами этого у меня пока не все гладко, поэтому надо проверять обе формулы на соответствие экспериментальным данным.

 

 

v= dv2 + v0*(1 – b1*cos(A1)) / (1 – b2*cos(A2)) + dv1                            (3-2-1)

 

v= (v0 + dv2) *(1 – b1*cos(A1)) / (1 – b2*cos(A2)) + dv1                         (3-2-2)

 

dv1= v0*(Ve1/Vs -1)*sin (A1)                                                                      (3-2-11)

 

dv2= v0*(Ve2/Vs - 1)*sin (A2)                                                                     (3-2-12)

 

 

 

Рис. 19. Сравнение результатов расчетов частоты принимаемого сигнала по различным формулам для общего эффекта Доплера при изменении углов Q2 и Q12 (источник движется параллельно горизонту со скоростью b2=14/20 при скорости сигнала 20 м/с, а приемник покоится на высоте 50 м). Темно-синяя кривая 3, синяя 3-2-1, черная 4-3 и 2 как 4-5, зеленая 2, а темно-зеленая 2, но с аберрационными поправками 3-2-1. Скриншот программы Dopler4.

 

 

А вот как раз проверить мои формулы (3-2) при релятивистских скоростях по экспериментальным данным я, к сожалению, пока не могу, т.к. единственные корректные данные были только в экспериментах Победоносцева и К, но и они не регистрировали пролетным методом скорость пучка ионов. Но, давайте, хотя бы из любопытства посмотрим, что у нас получится, если мы посчитаем по формулам (4-3), (2) и (2) с аберрационными поправками, которые будут учитываться согласно формуле (3-2-1) только для источника излучения, т.к. спектрограф (приемник) покоился. А использовать в расчете будем формулу (2), а не (3) потому, что при расчете по моей формуле (3) запаздывающий угол A2 находится по текущему углу Q2 и программа Dopler4, на которой я произвожу расчеты, воспринимает угол 77 градусов, как текущий и по нему рассчитывает запаздывающий угол, а уже потом производит расчет частоты по запаздывающему углу А2, но выдает результат расчета и строит все графики по углу Q2, т.е. так же, как и для всех остальных формул. А в экспериментах Победоносцева и К коллиматором задается угол уже запаздывающий, т.е. A2, поэтому для нашего случая сравнивать надо графики построенные по формулам (4-3) и (2) с аберрационными поправками (3-2-1), где этот запаздывающий угол воспринимается как текущий Q2 (в таблице это будет результат 3-2-1).

 

 

Как видим, все расчетные данные значительно отличаются от наблюдаемых и к тому же данные по формулам (4-3) и (3-2-1) практически совпадают и не возможно даже сказать какая из этих формул лучше, чем другая, отражает наблюдаемые данные. Но такие близкие результаты получаются только при малых скоростях, а при скорости источника 0,3*Vs у нас будет уже смещение для (4-3)=-14,74, а для (3-2-1)=-17,56 при угле наблюдения 77 градусов, хотя при угле 180-77=103 градуса результаты все равно будут очень близкими - для (4-3)=+78,12, а для (3-2-1)=+79,54. Но, не в условиях эксперимента, где лучи выделялись коллиматором строго под углом 77 градусов, а в реальных условиях, где будет и эффект запаздывания сигнала по координатам, расхождения в данных будут очень заметными (см. синие кривые на рис. 19).

 

 

 

 

 

Табл. 1. Наблюдаемые данные для смещения линии иона водорода 656,28 нм в красную dLk и синюю dLs стороны при разных скоростях ионов и расчетные данные по разным формулам, где красное смещение наблюдается при угле 180-77=103 градуса, а синее при угле 77 градусов.

 

E, кэВ	b2=V2/c	dLk	dLk (4-3)	dLk (2)	dLk (3-2-1)	dLs	dLs (4-3)	dLs (2)	dLs (3-2-1)
150	0,01264	1,72	1,919	1,866	1,917	-1,68	-1,814	-1,866	-1,815
175	0,01365	1,91	2,076	2,015	2,077	-1,86	-1,954	-2,015	-1,957
180	0,01385	1,87	2,108	2,045	2,106	-1,81	-1,982	-2,045	-1,984
200	0,01460	1,97	2,226	2,155	2,224	-1,90	-2,086	-2,155	-2,088
210	0,01496	2,05	2,282	2,209	2,281	-1,96	-2,135	-2,209	-2,137
225	0,01549	2,11	2,366	2,287	2,364	-2,05	-2,208	-2,287	-2,211
250	0,01632	2,16	2,497	2,409	2,495	-2,09	-2,322	-2,409	-2,325
260	0,01665	2,30	2,549	2,458	2,547	-2,20	-2,367	-2,458	-2,370
275	0,01712	2,37	2,624	2,527	2,622	-2,28	-2,432	-2,527	-2,434
300	0,01788	2,40	2,745	2,640	2,743	-2,29	-2,535	-2,640	-2,538
1500	0,04000	6,24	6,436	5,905	6,427	-5,40	-5,384	-5,905	-5,402
1750	0,04315	6,87	6,988	6,370	6,978	-5,75	-5,764	-6,370	-5,786
2000	0,04618	7,34	7,526	6,818	7,515	-5,95	-6,124	-6,818	-6,148

 

 

К сожалению при угле 77 градусов и более, как мы видим на рис.19, расхождения между данными рассчитанными по формулам (4-3) и (2) с аберрационными поправками (3-2-1) будут небольшие, что делает данные эксперимента Победоносцева и К мало пригодными для нашего анализа, но при углах менее 77 градусов расхождения в расчетных значениях по этим двум формулам будут очень заметными. Вот только у меня нет в распоряжении таких корректных данных, чтобы проверить их формулами (4-3) и (2) с аберрационными поправками (3-2-1). При этом, даже, если мы рассчитаем аберрационные поправки dv1 и dv2 не приблизительно, а точно, то для данных в эксперименте Победоносцева и К нам это ничего не даст. Ведь расхождения в данных рассчитанных по формулам (3-2-1) и (3-2-2), как с точными значениями аберрационных поправок, так и с приблизительными, будут отличаться между собою при углах и при скоростях, которые были в эксперименте, только в 4-м знаке, а экспериментальные значения приведены с точностью до 3-го знака.

 

 

Но, если кого-то интересует именно точный теоретический расчет этих поправок, то я приведу его, т.к. при больших скоростях различия между точным расчетом и приблизительным вдали от угла 90 градусов станут заметными. На рис. 20 Вы видите четыре расчетные схемы и ниже соответствующие им формулы для расчета аберрационных поправок dv1 и dv2 для источника и приемника при углах менее 90 градусов и более 90 градусов. При этом, обратите внимание, что углы А1 и А2 для приемника и источника отсчитываются в этом расчете по азимутоидальной схеме, т.е. от вектора скорости источника или  приемника влево и вправо до вектора луча зрения с источника на приемник от 0 до 180 градусов и эти углы берутся всегда положительные. А так же эти углы определяются между вектором скорости источника и вектором суммарной скорости и вектором скорости приемника и вектором скорости распространения сигнала и в расчетах, когда эти углы больше 180 градусов, используются углы В1=180-А1 и В2=180-В2.   

 

Рис. 20. Расчетные схемы для определения эффективных (суммарных) скоростей для источника и приемника при углах наблюдения меньше 90 градусов и больше 90 градусов.

 

 

Ve2 = sqrt(Vs ^ 2 - (V2 * sin(A2)) ^ 2) + V2 * cos(A2)                        (A2 <= pi/2)           (11-2)

Ve2 = sqrt(Vs ^ 2 - (V2 * sin(B2)) ^ 2) - V2 * cos(B2)                          (A2 > pi/2)

dv2 = v0 * (Ve2 - Vs - V2 * cos(A2)) / Vs                                                                            (3-2-22)

 

Ve1 = sqrt((Vs - V1 * cos(A1)) ^ 2 + (V1 * sin(A1)) ^ 2)                        (A1 <= pi/2)          (9-2)

Ve1 = sqrt((Vs + V1 * cos(B1)) ^ 2 + (V1 * sin(B1)) ^ 2)                        (A1 > pi/2)

dv1 = v0 * (Ve1 - Vs + V1 * cos(A1)) / Vs                                                                             (3-2-21)

 

 

Таким образом, т.к. значения рассчитанные и по моим формулам (3-2) и по релятивистской формуле (4-3) все таки отличаются от наблюдаемых данных, то, если в эксперименте Победоносцева и К скорости соответствуют реальным, значит надо менять расчетные формулы. Но, если изменять релятивистскую формулу, то надо отказываться от СТО, а, если изменять мою формулу, то значит надо глубже разобраться с эффектом аберрационного смещения частоты излучения и поглощения. Тем более, надо подойти более внимательно к этому эффекту, т.к. в экспериментах, аналогичных рассмотренным нами с центрифугами, но при распространении звукового сигнала [1], поперечный эффект тоже наблюдался, но происходило увеличение частоты принимаемого сигнала при приближении динамика к микрофону (см.  рис. 21), где скорость динамика V2= 57 м/с, а частота сигнала 3...4 кГц.

 

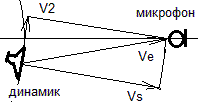
Рис. 21. Схема установки для наблюдения поперечного эффекта Доплера при распространении звука.

 

Хотя, возможно, что это связано с тем, что и у использовавшегося в экспериментах динамика, который крепился на стенке ротора, излучение не было узконаправленным перпендикулярно плоскости диффузора, и микрофон, который был установлен неподвижно за пределами ротора, мог принимать излучение не строго при угле 90 градусов, т.е. частично тут мог быть и продольный эффект Доплера, а в этом случае эффективная (суммарная) скорость Ve получалась больше Vs, как это изображено на рис. 21. Поэтому, чтобы этот эксперимент был чисто аберрационным, надо было сделать узкий канал, по которому сигнал от динамика мог распространяться строго под углом 90 градусов. Но в любом случае, окончательно вопрос об эффекте типа звездной аберрации пока не закрыт и вполне возможно, что он наблюдается не только при распространении света. А, т.к. эксперимент с динамиком и микрофоном не такой сложный, как с ионами или с мессбауэровскими центрифугами, то я недеюсь, что в ближайшее время его кто ни будь осуществит и не только в варианте поперечного эффекта. А кроме этого, сейчас надо будет внимательно проанализировать и все подобные эксперименты, а не только связанные со светом, например, эксперимент Майкельсона-Морли, т.к. возможно, что и в этих экспериментах наблюдается эффект звездной аберрации и эти данные тоже помогут уточнить некоторые моменты, которые при моем рассмотрении эффекта Доплера остались спорными.

 

 

А вот, что касается эффектов с замедлением времени то, как я постоянно пишу, я их просто считаю фокусами Эйнштейна, но, т.к. мы анализировали и его формулу для эффекта Доплера, то пришлось заниматься и его фокусами. А в рамках нашего рассмотрения именно эффекта Доплера надо сделать однозначный вывод о том, что релятивистская формула эффекта Доплера не имеет никакого отношения к действительности, а именно к эффекту Доплера, и, соответственно, и замедление времени на движущихся объектах, которое в экспериментах, связанных с эффектом Доплера, пытаются найти, тоже является просто мифом, а, следовательно, и нет никакой необходимости притягивать сюда за уши теорию относительности с ее геморроями. А сама СТО, родившая релятивистскую формулу эффекта Доплера, является просто мифической теорией для развлечения математиков, но истинным релятивистам никакими логическими доводами этого доказать никак нельзя. Поэтому, приходится уповать только на эксперименты, которые говорят сами за себя лучше любых доказательств.

 

 

  

 

 

 

3. Проверка различных формул для эффекта Доплера при проведении вычислительных экспериментов на математической модели этого эффекта.

 

 

А сейчас давайте посмотрим, какие результаты покажут различные формулы для эффекта Доплера в вычислительных экспериментах при распространении условного сигнала в пространстве между источником и приемником без учета аберрационных поправок, возникающих в самих источнике и приемнике. Вычислительные эксперименты будем проводить на программе Dopler4, в которой (по сравнению с предыдущими версиями) добавлен расчет по всем известным мне релятивистским формулам и убран расчет по формуле Замятина, а также добавлена форма для расчетов по центрифугам. К сожалению, после публикации 1-ой редакции статьи я понял, что многие до сих пор имеют смутное представление о том, что такое математическая модель (ММ) и что такое вычислительный эксперимент, поэтому возникло много вопросов о приведенных мною наблюдательных данных, полученных при проведении вычислительного эксперимента. В связи с этим я решил прямо в этой статье устроить маленький ликбез по этим вопросам, изложив вкратце материал своих работ [14, 15] по моделям и имитаторам и немного коснуться вопроса о вычислительном эксперименте (см. Приложение 2). К тому же, уравнения математической модели для описания эффекта Доплера, т.к. здесь рассматривается прямолинейное равномерное движение, у нас получились самые элементарные. А, т.к. система у нас небольшая - состоит из источника, приемника и предаваемого сигнала, то и уравнений получилось не много, поэтому для примера очень подойдет именно модель эффекта Доплера.

 

 

Уравнения этой модели я привожу ниже, но можете посмотреть их и в исходниках программы Dopler4 - это файл form1.frm (можно просмотреть обычным Блокнотом в конце файла, т.к. код начинается после описания самой формы). Мы при проведении вычислительных экспериментов на этой модели будем как бы решать эту систему уравнений численными методами, т.е. с использованием множества мелких итераций с шагом решения по времени P0. А, кого интересует решение этой системы уравнений полуаналитически, т.е. когда мы не получаем как при аналитическом решение системы уравнений окончательный ответ, как, например, нижеприведенная формула (10*), а решаем систему уравнений аналитически, но по частям для каждого отдельного этапа, могут ознакомиться с ним в Приложении 1. Там я даю расчет частоты принимаемой движущимся приемником для нескольких первых периодов движущегося на источнике передатчика сигналов.

 

X1=X1+VX1*P0

Y1= Y1+VY1*P0

X2=X2+VX2*P0

Y2= Y2+VY2*P0

R=((X1-X2n)^2+(Y1-Y2n)^2)^0,5

Rs=Rs+Vs*P0

T=T+P0

где X1, Y1, X2, Y2 - текущие координаты, соответственно, приемника и источника

X2n, Y2n - координаты источника в момент времени, когда сигнал о начале или конце периода колебаний был излучен источником.

VX1, VY1, VX2, VY2 - скорости приемника и источника по осям координат

Rs - радиус сферы, до которой распространился сигнал от источника с момента его излучения и до текущего времени

R - расстояние между текущим положением приемника и положением источника в тот момент времени, когда сигнал о начале или конце периода колебаний был излучен источником.

Vs - скорость распространения сигнала

T - текущее время

P0 - шаг интегрирования (шаг решения уравнений).

 

Многие, посмотрев на эти уравнения, сильно удивятся и зададутся вопросом - неужели это и есть модель для эффекта Доплера. Да, это самая, что ни на есть настоящая математическая динамическая модель для эффекта Доплера. А вот все теоретические формулы, которые мы рассмотрели ранее (2, 3, 4-1...4-6), являются математическими имитаторами этого эффекта и таких имитаторов может быть много (кстати, и моделей для сложных систем тоже может быть несколько). Причем, эти имитаторы, иногда бывают окончательным решением (пусть и с какими то допущениями) системы уравнений являющейся ММ системы, но чаще всего это просто аппроксимация какими то уравнениями экспериментальных данных, хотя иногда такая аппроксимация и выглядит как отражающая логические закономерности процессов, описанных ею. И именно такими имитаторами и являются все рассмотренные нами формулы эффекта Доплера, но почти все видят в них больше, чем простые аппроксимации, и пытаются найти какой-то глубинный смысл. А эти имитаторы являются просто расчетными формулами, которые упрощают нам процесс вычислений при рассмотрении эффекта Доплера. Хотя надо заметить, что точные аналитические решения уравнений ММ действительно позволяют нам понять рассматриваемое явление, но это бывает очень редко, т.к. почти все окружающие нас системы описываются нелинейными дифференциальными уравнениями, а последние аналитически не решаются и остается только численное решение таких систем уравнений.

 

При этом по различным расчетным формулам для эффекта Доплера мы можем определить только мгновенную частоту принимаемого сигнала в конкретных положениях приемника, чего в реальности быть не может. Поэтому, для сравнения наблюдаемых и расчетных данных, мы будем находить эту расчетную частоту в начале приема условного периода и в конце. А потом будем находить среднее расчетное значение частоты для этого условного периода и сравнивать его с наблюдаемым значением частоты, полученным по разности времени прихода сигнала, т.е. по его наблюдаемому в эксперименте периоду. Хотя, можно было бы определять и по расчетным формулам сразу среднюю частоту приема сигнала, но для этого надо было бы в расчетных формулах использовать углы Q и A для положения приемника в середине принимаемого периода. Например, если бы у нас источник был неподвижен в точке O, то это было бы положение между точками N1 и N2 для угла A, как это показано на рис. 22. Но я считаю, что это бы только запутало расчеты, да и результат при этом получился бы с большой погрешностью, поэтому будем вычислять по формулам две принимаемые частоты (в начале и в конце расчетного периода), а потом находить среднюю частоту. 

 

 

 

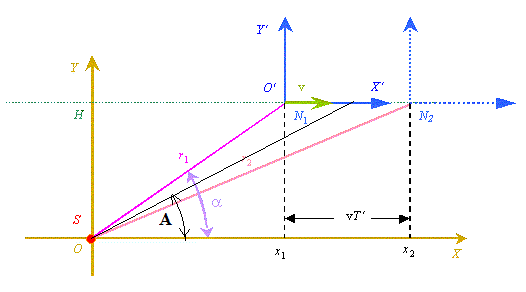
Рис. 22. Схема к расчету периода принимаемого сигнала для общего эффекта Доплера при неподвижном источнике (воспроизведено из работы [12]).

 

 

Вообще то, можно было бы и не проводить вычислительный эксперимент на модели системы, где движутся по заданным уравнениям источник, приемник и сигнал, а решить аналитически эту систему уравнений и получить формулу для наблюдаемой частоты принимаемого сигнала, т.е. именно формулу для эффекта Доплера, но в виде имитатора, т.е. в том виде, как мы привыкли говорить об эффекте Доплера. При этом саму частоту мы определили бы так же по периоду между двумя моментами времени прихода сигнала, но я считаю, что и это еще больше запутало бы рассмотрение этого вопроса и к тому же мы бы лишились наглядности этого процесса, который при проведении вычислительного эксперимента в программе Dopler мною еще и анимирован. Да и аналитическая формула получилась бы слишком громоздкой, т.к., например, в работе [12] такая формула (10*) уже для частного случая движения только приемника и только по одной оси координат получилась очень сложной (к тому же, в расчете используется только один угол, что является ошибкой). А для общего случая, т.е. и для движения источника и по двум осям координат и при расчете по двум углам, она будет на порядок или на два больше и это лишит нас простоты и наглядности, которую дает вычислительный эксперимент. Кстати, авторы [12] пренебрегли тем обстоятельством, что мы вычисляем наблюдаемую частоту по периоду времени между двумя точками приема начала и конца принимаемого периода сигнала, т.е. примерно для угла А, и поэтому, используя данные, полученные ими по формуле (10*), которую выводили по рис. 22 с использованием угла α, они пришли к выводу о том, что наблюдают и поперечный эффект Доплера.

 

 

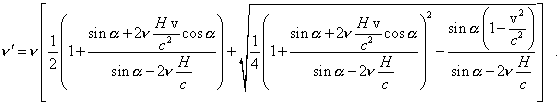      (10*)

Рис. 23. Графики зависимости относительного изменения частоты, принимаемой движущимся наблюдателем при неподвижном источнике в общем эффекте Доплера в функции от изменения угла α. Синяя кривая по СТО, сиреневая - классика (воспроизведено из работы [12]).

 

Но, если они устранят эту ошибку и будут определять на рис. 22 угол α не в направлении на точку N1, а в направлении на середину отрезка между точками N1 и N2, то на рис. 23 у них в той точке графика, где у них указан угол pi/2, получится угол немного меньше, а угол α будет равен именно pi/2, но немного правее. Таким образом, их график на рис. 23 пройдет в точке pi/2 ровно через значение частоты передатчика отложенной по вертикальной шкале и никакого поперечного эффекта Доплера не будет. Кстати, для тех, кто заинтересуется этой работой, отмечу особо, что ни только никаких вычислений по расчетной формуле для общего эффекта Доплера (2) они в этой работе не производят, но они вообще этой формулы не приводят в своей работе. Это я к тому, чтобы, ознакомившись с этой работой, некоторые читатели не подумали, что у них поперечный эффект Доплера получился не из-за методологической ошибки определения наблюдаемой частоты приема, а именно из классической формулы (2). А у меня при проведении вычислительных экспериментов никакого поперечного эффекта Доплера не наблюдается.

 

 

Рассмотрим движение источника и приемника, а также распространение волн генерируемых передатчиком с заданной частотой v0 и распространяющихся в пространстве между источником и приемником, как это изображено на рис. 24, где вычислительный эксперимент выполняется на математической модели (ММ) описанной выше. Конкретно здесь v0=0,2 Гц и получается один условный период T00=5 с, который используется в расчетах для начала передачи сигнала в начале каждого нового периода колебаний передатчика. А мы в тот момент времени, когда этот сигнал достигает движущегося приемника, фиксируем время прихода и потом находим промежутки времени между этими соседними зафиксированными моментами времени прихода сигнала, т.е. определяем наблюдаемый период принимаемого сигнала. И ниже в табл. 2, как наблюдения, я и привожу данные вычислительного эксперимента, которые получились при исходных данных заданных в полях формы программы на рис. 24. При этом для данных, рассчитанных по формулам Эйнштейна, я сначала привожу значения, которые получаются по его формуле без релятивистского множителя (4-4), т.к. в моей модели не отражено замедление времени, а потом даю и по формулам (4-1), (4-3) и (4-5).

 

 

 

Рис. 24. Вычислительный эксперимент по распространению волн от движущегося на нулевой высоте со скоростью 10 м/с источника 2 и принимаемых движущимся на высоте 50 м со скоростью 6 м/с приемником 1. В зеленых кружках указаны номера условных периодов между моментами времени, когда передатчик сделал одно колебание и приемник принял сигналы начала и конца этого колебания. Скриншот программы Dopler4. 

 

 

 

 

 

 

Табл. 2. Наблюдаемые и расчетные данные частоты принимаемого сигнала при распространении условного сигнала с частотой передатчика 0,2 Гц.

 

№ периода	наблюдения	Юдин	Лоренц	4-4	4-1	4-3	4-5
1	0,256	0,256	0,224	0,218	0,223	0,216	0,204
2	0,242	0,241	0,206	0,205	0,209	0,201	0,187
3	0,221	0,221	0,192	0,190	0,194	0,187	0,174
4	0,202	0,202	0,183	0,178	0,182	0,177	0,166
5	0,189	0,189	0,179	0,171	0,175	0,171	0,162
6	0,182	0,183	0,177	0,167	0,171	0,168	0,160
7	0,179	0,179	0,176	0,165	0,168	0,167	0,159

 

 

Как видим, совпадение наблюдаемых данных с расчетными при распространении условных волн сигнала имеется только при расчете по моей формуле, а все остальные формулы дают очень большую ошибку, но еще более наглядно это видно по графику на рис 25. А небольшое отклонение моих расчетных данных от наблюдаемых имеется только вблизи угла 90 градусов, но это объясняется не ошибкой в моей формуле, а погрешностью определения для графика среднего угла, по которому мы и наносим на график наблюдаемое значение частоты приема. Это связано с тем, что вблизи угла 90 градусов функция тангенса имеет большую нелинейность и поэтому при таком большом расчетном периоде мы при вычислении среднего угла для этого наблюдаемого периода получаем несоответствие между наблюдаемым периодом для среднего угла и наблюдаемым периодом между двумя заданными углами. И чем больше у нас будет расстояние между двумя углам наблюдения, пройденное приемником за один расчетный период (особенно вблизи угла 90 градусов), тем больше будет эта погрешность на графике, построенном в функции от средних углов для рассчитываемого периода приема сигнала. Хотя, как это видно из данных в таблице 2, значение самого расчетного периода, рассчитанного по средней частоте, которая в свою очередь рассчитана как среднее значение двух принимаемых частот для двух углов (начала периода и конца), очень хорошо согласуется с наблюдаемым значением.

 

 

 

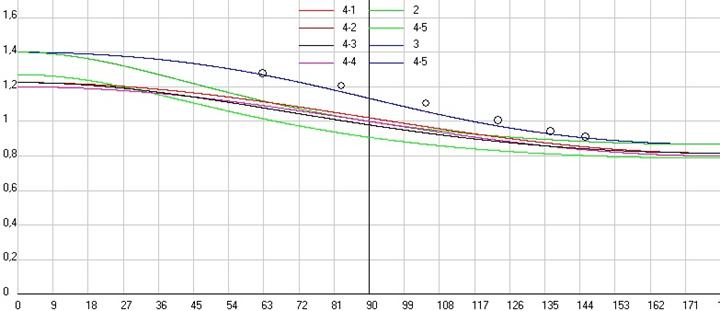
Рис. 25. Сравнение наблюдаемых данных (частоты принимаемого сигнала) вычислительного эксперимента (кружки) и расчетных значений (кривые), полученных по различным формулам при движении приемника на высоте 50 м со скоростью 6 м/с, а передатчика на нулевой высоте со скоростью 10 м/с (2- зеленая кривая и как вариант 4-5- светло-зеленая, 3- синяя, 4-1, 4-3 и 4-4- соответственно, красная, черная и сиреневая). Скриншот программы Dopler4. 

 

 

И, если мы изменим начальные координаты (Y1n=20 м и X2n=40м), т.е. так, чтобы за один период его угол начала приема и конца изменялись еще больше, то ошибка на графике, построенном по среднему углу приема, станет еще больше (см. рис. 26). Хотя рассчитанное среднее значение частоты по двум положениям приемника для этого условного периода, как и данные в таблице 2, будет очень хорошо согласовываться с наблюдаемым значением. Таким образом, сама моя формула дает всегда правильный результат по принимаемому периоду сигнала, но, когда мы строим график для этого результата по среднему углу приема, то у нас получается несоответствие между теоретическим графиком и проставленной точкой. Причем это несоответствие при построении графика может быть больше или меньше в зависимости от того какова нелинейность функции тангенса между точками начала приема периода сигнала и его конца, т.е. мы можем попасть или на почти линейный участок и тогда расхождения будут небольшие или на очень нелинейный и тогда расхождения будут большие. Но для реальных частот излучения, которые есть у звука или света и обычно наблюдаемых скоростях источника и приемника эта разность в углах для одного периода будет очень не большой и такого несоответствия при построении графиков наблюдаться не будет.

 

 

 

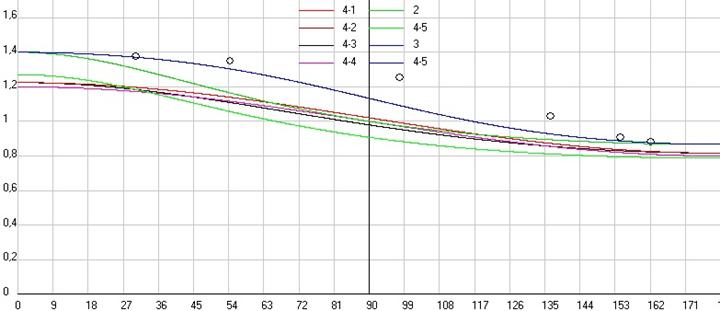
Рис. 26. Сравнение наблюдаемых данных (частоты принимаемого сигнала) вычислительного эксперимента (кружки) и расчетных значений (кривые), полученных по различным формулам при движении приемника на высоте 20 м со скоростью 6 м/с, а передатчика на нулевой высоте со скоростью 10 м/с (2- зеленая кривая и как вариант 4-5- светло-зеленая, 3- синяя, 4-1, 4-3 и 4-4- соответственно, красная, черная и сиреневая). Скриншот программы Dopler4. 

 

 

Таким образом, наши вычислительные эксперименты, во-первых, опровергают наличие поперечного эффекта Доплера в различных классических формулах, когда рассматривается только процесс распространения волн в пространстве между источником и приемником, а, во-вторых, доказывают справедливость именно моей формулы для отражения этого эффекта, которая позволяет получить очень точные данные. Ну, а про релятивистские формулы тут и говорить нечего, т.к. все они дают очень плачевные результаты. Ведь их релятивистский множитель оказывает влияние сразу на весь результат при этом эффекте, а должен был повлиять только на аберрационные поправки, которые не учитывались в ММ, т.е. не должны были отражаться имитатором (релятивистскими формулами).

 

 

Да, я при проведении вычислительных экспериментов на ММ не изменял темп течения времени и решал задачу в математическом времени, т.е. с постоянным шагом Р0, поэтому сторонники СТО могут заявить, что, если бы темп течения времени изменялся, то наблюдаемые значения совпали бы с расчетными значениями по релятивистской формуле. Ну, во-первых, не совпали бы потому, что все эти релятивистские формулы не учитывают запаздывание сигнала по координатам, а, во-вторых, это бы все равно ничего нам не дало, т.к., если бы мы включили в модель замедление времени, то, естественно, его надо было бы отражать и в классическом имитаторе. А при этом именно замедление времени правильно бы отразили все имитаторы - и релятивистские и классические, но запаздывание по координатам релятивистские имитаторы бы так и не отразили. Да и потом, чтобы моделировать такое чудо, как замедление темпа течения времени, надо хотя бы знать, какая из трех релятивистских формул самая правильная из неправильных. Но пока сторонники СТО даже не могут договориться между собою какую из формул надо использовать в подобных экспериментах при учете в ММ замедления времени. А это надо знать, чтобы знать где в ММ время должно замедлятся (на приемнике для формулы (4-1), на источнике для формулы (4-3) или и там и там для формулы (4-5)). Ведь, как мы видим, все релятивистские имитаторы дают разные значения принимаемой частоты для общего эффекта Доплера, поэтому самой правильной формулой из неправильных может быть только одна.

 

 

А вот, что касается аберрационного эффекта в наших вычислительных экспериментах, то я его не моделировал, т.к., как я писал выше, пока и сам не до конца разобрался с этим вопросом. Но, например, при наблюдении чисто поперечного эффекта, когда у нас и источник и приемник будут двигаться с одинаковыми скоростями равномерно и параллельно друг другу (источник немного впереди), то здесь этот эффект никак не скажется на результатах вычислительного эксперимента. В этом случае, так же, как и с центрифугами, когда и источник излучения и поглотитель размещены на стенке ротора, у нас оба аберрационных эффекта взаимно компенсируются. А вот именно поперечного эффекта Доплера, связанного с относительным движением источника и приемника, которые и воспроизводятся в вычислительном эксперименте, не будет в принципе. Да, я постараюсь в будущем создать ММ отражающую все явления в эффекте Доплера, чтобы проверить созданный мною имитатор (3-2) на адекватное отражение этого явления, но пока можно пользоваться и им, т.к. он вполне удовлетворительно отражает все процессы, которые протекают при наблюдении  эффекта Доплера.

 

 

При этом надо всегда понимать, что даже если наши различные теоретические зависимости (имитаторы) и не всегда идеально аппроксимируют наблюдаемые данные, но, например, для эффекта Доплера они позволяют значительно упростить расчет, то это очень важно с практической точки зрения, т.к. не надо использовать для этого ММ эффекта. Ведь Коперник предложил свою систему мира именно для упрощения людьми астрономических расчетов, а не для того, чтобы насолить церкви, ошибочно утверждавшей, что Солнце вращается вокруг Земли, и не для того, чтобы показать всем какой он крутой альтернативщик. А вот зачем Эйнштейн предложил свою формулу для эффекта Доплера совершенно не понятно, т.к. мало того, что она только запутала этот вопрос, но и все ее разновидности дают результаты очень далекие от наблюдаемых данных. А то, что время не замедляется на движущихся объектах, и, следовательно, нет в Природе поперечного эффекта Доплера, мы с Вами убедились, проанализировав результаты различных натурных экспериментов, где авторы пытались найти это замедление. В общем, получается, что СТО не только не соответствует результатам натурных экспериментов, ни и не может даже сказать какой, из рожденных ею формул, надо пользоваться при проведении вычислительных экспериментов, т.е. является просто математической игрушкой.

 

 

 

  

 

 

                                                                           Выводы

 

1. - Все классические формулы, которые дают поперечный эффект Доплера, являются ошибочными, т.к. не подтверждаются вычислительным экспериментом, а сам поперечный эффект в них появляется в  результате различных ошибок сделанных при выводе формулы для эффекта Доплера. Но эффект, подобный поперечному эффекту Доплера, т.е. аберрационный эффект Доплера, при этом наблюдаться будет и определять его надо по моей формуле (3-2). При этом в формуле Лоренца (2) должно учитываться запаздывание сигнала по координатам, т.е. за основу формулы (3-2) надо брать мою формулу (3).

 

2. - Все релятивистские формулы, которые дают поперечный эффект Доплера, являются ошибочными, т.к. не подтверждаются натурными экспериментами, в которых нет методических ошибок, а также противоречат друг другу для общего эффекта Доплера, что не позволяет даже выбрать одну из них для сравнения с данными вычислительного или натурного эксперимента.

 

3. - Т. к. различные релятивистские формулы для эффекта Доплера, не имеют к этому физическому явлению никакого отношения, но непосредственно вытекают из СТО, то и сама СТО не имеет никакого отношения к действительности и является просто игрушкой для математиков.

 

 

 

                                                                        

                                                                   Список литературы

 

1. – А.Г. Замятин Принцип близкодействия. Свердловск, 1988, 153 с. http://yadi.sk/d/mpuZzuId1xkL5

2. – Н.В.Купряев Классический эффект Доплера http://www.sciteclibrary.ru/rus/catalog/pages/8803.html

3. – О.Е.Акимов О формуле, описывающей классический эффект Доплера http://sceptic-ratio.narod.ru/fi.htm#Doppler

4.- Дж.Х. Тэйлор (мл.) Двойные пульсары и релятивистская гравитация (Нобелевская лекция. Стокгольм, 8 декабря 1993 г.) Успехи физических наук, Июль 1994 г. Том 164, №7

5. - Н.М. Акельев Специальная теория относительности А. Эйнштейна – величайшая афера в истории физики и альтернативная ей концепция Лоренца-Фиджеральда-Планка. Волгоград, 2013, 166 с http://akelevnm.narod.ru/aboutsto.htm

6 - У.И. Франкфурт, А.М. Френк Оптика движущихся тел. М.: Наука, 1972  ссылка  http://ritz-btr.narod.ru/frankfurt/frankfurt.html

7. - C. Novotny and other Sub-Doppler laser spectroscopy on relativistic beams and tests of Lorentz invariance. Physical Reviev, A 80, 022107, 2009

8. – А.Эйнштейн К электродинамике движущихся тел. Собрание научных трудов. Том 1. М.: Наука, 1965, 701 с.

9.- Е.А. Бутяев Загадки природы Гл. 4 О противоречивости различных интерпретаций красного смещения http://butjaev.narod.ru/BIB/gl4.pdf

10. - С.Ю. Юдин Влияние скорости гравитации на смещения параметров орбит планет. Волгоград, 2013, 144 с. http://modsys.narod.ru

11. - И.В. Савельев Курс общей физики. т. 2, М.: Наука, 1988 г., 496 с.

12. - С.Б. Каравашкин, О.Н. Каравашкина О поперечном эффекте Доплера в рамках классического формализма Харьков, 11 с. http://selftrans.narod.ru/v5_1/doppler/doppler47/doppler46rus.html

13. - С.Ю. Юдин Опять о принципе наименьшего действия. Волгоград, 2010, - 43 с http://modsys.narod.ru/Stat/Stat_Est/Princip2/princip21.html

14. - С.Ю. Юдин Моделирование систем и оптимизация их параметров. Волгоград, 2006, 213 с.   программа-просмотрщик с анимациями  http://modsys.narod.ru/Stat/Reader5m_exe.rar , текстовый файл http://modsys.narod.ru/Stat/Reader5m_doc.rar

15. – С.Ю.Юдин Модели и имитаторы. труды 5-ой международной научно-технической конференции Компьютерное моделирование 2004. Часть 1. СПб.: Нестор, 2004, 356 с. http://modsys.narod.ru/Stat/Stat_Est/Konf_SPB/mod_imi.html

16. - H.E. Ives The Doppler Effect Considered in Relation to the Michelson-Morley Experiment, J.O.S.A, Nov. 1937, vol. 27 pp. 389-392. http://www.conspiracyoflight.com/Ives/HerbertIves1937c.pdf

17. - H.E. Ives, G.R. Stilwell An Experimental Study of the Rate of a Moving Atomic Clock, J.O.S.A, Jul. 1938, vol. 28, No 7, pp. 215-226. http://www.conspiracyoflight.com/Ives/HerbertIves1938a.pdf

18. - H.E. Ives, G.R. Stilwell An Experimental Study of the Rate of a Moving Atomic Clock. II, J.O.S.A, May 1941, vol. 31 pp. 369-374. http://www.conspiracyoflight.com/Ives/Herbert_Ives-Rate_of_a_Moving_Clock_II.pdf

19. -  А.А. Детлаф, Б.М. Яворский Курс физики. Том III. Волновые процессы. Оптика. Атомная и ядерная физика. М.: Высшая школа, 1979. - 511 с. http://eqworld.ipmnet.ru/ru/library/books/DetlafYavorskij_t3_1979ru.djvu

20. - Л.Д. Ландау, Е.М. Лифшиц Теоретическая физика: Учеб. пособие в 10-ти т.Т.2. Теория поля. - 7-е изд. М.: Физматлит, 1988. - 512 с.   

21.- Л.А. Победоносцев, Я.М. Крамаровский, П.Ф. Паршин, Б.К. Селезнёв, А.Б. Берёзин   Экспериментальное определение доплеровского смещения линий водорода на пучках ионов H2+ в диапазоне энергий 150-2000 кэВ. Журнал технической физики, Том 59, в. 3, 1989 г., с. 84.

22. - S.P. Drake, A. Purvis Everyday relativity and the Doppler effect. American Association of Physics Teachers. 2014. http://dx.doi.org/10.1119/1.4830887

23. - C. H. Chang, J. H. Hsiao, and T. M. Hong  Optical Doppler Effect in a Medium  Chinese Journal of Physics Vol. 47, No. 4. August 2009.

24 - У.И. Франкфурт Оптика движущихся сред и специальная теория относительности. Эйнштейновский сборник. 1977, стр. 257-326.

25. - B. Botermann and other Test of Time Dilation Using Stored Li+ Ions as Clocks at Relativistic Speed. arXiv: 1409.7951v1. 2014     http://arxiv.org/pdf/1409.7951.pdf

26. - G. Saathoff and other Improved Test of Time Dilation in Special Relativity. Phisycal Review Letters,   Vol. 91, No. 19, 2003

27. - В. Демтредер Лазерная спектроскопия: Основные принципы и техника эксперимента. М.: Наука. 1985. 608 с.

28. - Д.К. Чемпни и П.Б. Мун Отсутствие доплеровского сдвига при движении источника и детектора гамма-излучения по одной круговой орбите. Эйнштейновский сборник за 1978-1979 годы, М.: Наука, 1983, стр. 319-322.  http://acmephysics.narod.ru/archive_r/moon.zip

29.- D.C. Champeney, G.R. Isaak, A.M. Khan A time dilatation experiment based on the Mössbauer effect. Proceedings of the Physical Society. 85. 3. 583–593. 10.1088/0370-1328/85/3/317, 1965 http://iopscience.iop.org/0370-1328/85/3/317/pdf/0370-1328_85_3_317.pdf

30. - С.Г. Тигунцев О красном смещении http://www.sciteclibrary.ru/rus/catalog/pages/8788.html

31. - Теория относительности Эйнштейна подтверждена математикой. дискуссия на форуме dxdy

http://dxdy.ru/post97928.html#p97928

32.- W. Kundig Measurement of the Transverse Doppler Effect in an Accelerated System. Physical Review Vol. 129, No. 615, 1963.

33. - Р.В. Паунд О весе фотонов. Успехи физических наук, том 72, выпуск 4, 1960.     http://ufn.ru/ufn60/ufn60_12/Russian/r6012b.pdf

34. - R.V. Pound and J.L. Snider Effect of Gravity on Gamma Radiation. Physical Review 140, B788, 1965. http://www.fisica.uniud.it/URDF/laurea/idifo1/materiali/g5/Probl8_37II.pdf  

35. - A.L. Kholmetskii, T. Yarman and O.V. Missevitch  Kündig’s experiment on the transverse

Doppler shift re-analyzed. Phisical Scripta, 2008.

36. - A.L. Kholmetskii, T. Yarman, O.V. Missevitch and B.I. Rogozev Mössbauer experiments in a rotating system on the time dilation effect. International Journal of the Physical Sciences Vol. 6(1), pp. 84-92, 2011.

37. - Ю.И. Овсепян Некоторые особенности релятивистского доплер-эффекта. УФН, том 168, №9, 1998. http://www.mathnet.ru/links/999b4e721bf601770a437ffd23b79c7b/ufn1521.pdf

38. - К. Мёллер Теория относительности. Изд. 2-е. М.: Атомиздат, 1975, 400 с.

39. - А.Р. Стриганов, Н.С. Свинтицкий Таблицы спектральных линий нейтральных и ионизованных атомов. М.: Атомиздат. 1966. 899 с.

40. - G. Saathoff and other Test of time dilation by laser spectroscopy on fast ions. Can. J. Phis. Vol. 83, 2005, p. 425-434.

41. - S. Karpuk and other Test of Time by Laser Spectroscopy on Fast Ions (презентация).

42. - Б.Д. Агапьев, М.Б. Горный, Б.Г. Матисов, Ю.В. Рождественский Когерентное пленение населенностей в квантовых системах. Успехи физических наук, том 163, выпуск 9, 1993.  http://ufn.ru/ufn93/ufn93_9/Russian/r939a.pdf

43. - S.B. Reinhardt Measurement of Time Dilation by Laser Spectroscopy on Fast Stored Lithium Ions.

Dissertation of Doctor of Natural Sciences. Heidelberg. 2005.

 

 

P.S. Все мои работы (в последних редакциях) можно найти на моих сайтах в разделе "Научные работы", а всю другую литературу, использованную мною при написание статей, в разделе "Моя библиотека".

 

Первую редакцию статьи можно посмотреть здесь http://modsys.narod.ru/Stat/Stat_Est/Dopler1.html

или скачать архив статьи в формате .doc http://modsys.narod.ru/Stat/Stat_Est/Dopler1doc.zip

https://googledrive.com/host/0BwnV2Ac6zvhMalpOVGktQ1Jic1U/Stat/Stat_Est/Dopler1/Dopler1doc.zip

 

 

P.S.P.S.

Надеюсь, что данная статья не только помогла разобраться Вам с самим эффектом Доплера, но и помогла лучше понять сегодняшнее положение дел в науке, где организованные профессиональные группы (ОПГ), используя свое влияние, навязывают научной общественности свои взгляды на описание явлений Природы. Это делается и проведением экспериментов, выгодных этим ОПГ, и интерпретацией результатов уже проведенных экспериментов в рамках теорий, защищаемых этими ОПГ, и запретом на публикацию статей, не подтверждающих эти теории. И, хотя последнее время уже появилось много статей (спасибо Интернету), которые наглядно показывают ошибочность многих теорий (СТО, ОТО, квантовая механика), которые защищаются различными ОПГ, но я надеюсь, что и эту статью я написал не зря и она поможет читателям более наглядно увидеть ошибочность этих теорий.

  

Хотя, вообще-то, при написании этой статьи я первоначально и не думал, что дело зайдет так далеко, т.е. до СТО, ОТО и квантовой механики, и собирался только прояснить для себя некоторые моменты в моей формуле силы гравитационного взаимодействия тел (1), т.к. она получилась очень схожей с формулой (2) для эффекта Доплера. Но, в любом случае, то, что я хотел, я для себя прояснил и поэтому могу спокойно продолжать свое исследование по определению скорости гравитации, но уже внеся в свою формулу (1) аберрационные поправки. Кстати, Лаплас это уже делал, о чем я писал в работе [10], но он при этом рассматривал гравитацию с корпускулярной точки зрения.

 

Вот только сейчас у меня возник тупик, т.к. мне для дальнейшей работы по определению скорости гравитации нужны первичные наблюдательные данные (сырые) по двойному пульсару PSR 1913+16, но все, у кого они есть, т.к. являются членами одной ОПГ, под различными предлогами пока отказываются мне их предоставить. Поэтому, возможно, что я сейчас займусь рассмотрением вопроса описания в рамках классической механики процессов излучения и поглощения энергии атомами, а всех читателей, у кого есть такая возможность, попрошу посодействовать мне в получении данных наблюдений за двойным пульсаром PSR 1913+16.

 

                                                                                                                                        ПРИЛОЖЕНИЕ 1

 

 

 

Анализ классических формул Замятина и Акимова дающих поперечный эффект Доплера.

 

 

Как мы выяснили по результатам вычислительного эксперимента, никакого поперечного эффекта Доплера в классической формуле этого эффекта не должно быть. А у Каравашкиных этот эффект появляется из-за ошибки определения периода сигнала регистрируемого на приемнике только по одному углу. А вот откуда появился этот эффект в формуле Акимова мы сейчас выясним. Правда, как показал анализ литературных источников по эффекту Доплера, формула, которую пропагандирует сейчас Акимов, получена еще в работе Замятина [1]. Поэтому логичнее было бы говорить о формуле Замятина. К тому же у Акимова, например, вот в этой работе [3], изменяется скорость распространения сигнала (у Замятина она не меняется), и вывод этой формулы у него явно уступает выводу Замятина, хотя он у обоих не правильный. Сейчас ошибочность формулы Акимова активно критикует Купряев [2] и приводит свой вывод общей формулы для эффекта Доплера, который дает формулу Лоренца. Но все они, не считая мелких ошибок и не понимая того, что создают просто имитатор, сделали одну принципиальную ошибку, а именно они совершенно не рассматривают сам передатчик, генерирующий исходную частоту, которую и надо промодулировать этим эффектом по законам частотной модуляции. И это при том, что они совершенно не рассматривают аберрационные эффекты. Давайте рассмотрим их ошибки и начнем с вывода своей формулы Замятиным, который воспроизведем по рисунку из его же работы.

 

 

 

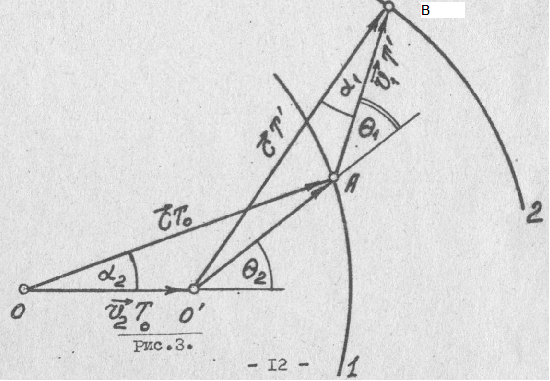
«Пусть движущийся со скоростью V2 источник в точке O создал некоторый фронт волны 1, зафиксированный далее также движущимся со скоростью V1 приемником в точке A в момент времени  t1. К этому моменту источник, перейдя в точку O’, создает следующий той же фазы фронт 2, который настигает удаляющийся приемник в точке B в момент t2. Требуется определить период принятых колебаний T’= t2 – t1 и частоту v’.

Из тр-ка O’BA отрезок O’A определится выражением

 

 

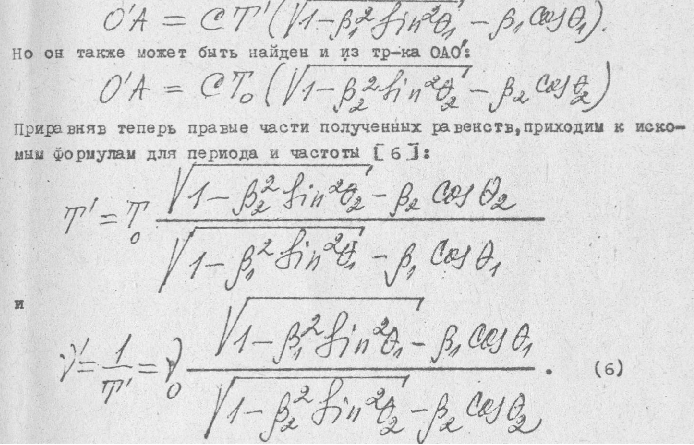
И к этой же самой своей формуле (6*) Замятин приходит и другим путем из формулы продольного эффекта Доплера, полученной самим Доплером

 

v’ = v0 * (C – V1) / (C – V2)      (1*)

 

   

 

 

Вот только я никак не могу взять в толк какое отношение вывод Замятина (Акимова, Купряева) имеет именно к эффекту Доплера, т.е. к изменению частоты принимаемого движущимся приемником сигнала, который излучается передатчиком на движущемся источнике, т.е. к частотной модуляции. Например, гудок паровоза является передатчиком, который генерирует сигнал с определенной частотой и который потом подвергается частотной модуляции движущимся источником, т.е. паровозом. При приближении паровоза мы слышим сигнал более высокой частоты, а при удалении - более низкой. А все эти авторы вообще ничего не пишут о частоте именно передатчика. У них за исходный сигнал принимается либо движение фронта ударной волны либо уже промодулированный источником сигнал передатчика. Конкретно Замятин рассматривает движение фронта ударной волны. И здесь у него время T и T’ не является никаким периодом колебаний, т.к. это просто время распространения сигнала, которое будет одинаковым и для ударной волны и для обычной волны при любой частоте передатчика, т.е. при любом периоде его колебаний. А у фронта ударной волны, которую создает источник, эта частота может зависеть только от скорости источника, а не формироваться искусственно, как у Замятина, когда новый фронт волны образуется при достижении предыдущим фронтом приемника. Но его не может быть у обычной волны передатчика (даже с заданной фазой сигнала), т.к. здесь можно говорить только условно о фронте волны при фазе равной нулю.

 

 

Вывод Замятина формулы для якобы эффекта Доплера, можно, наверное, как-то применить для распространения фронта ударных волн с учетом запаздывания сигнала по координатам, но никак не к эффекту Доплера. Но тогда надо и назвать этот эффект, который рассматривает Замятин, например, эффектом Маха, т.к. Мах первым определил формулу для конуса ударных волн при движении пули. Да, формула у Замятина получается вроде бы очень похожая на правду, но ведь и корова тоже очень похожа на быка, но любому человеку ясно, что она не бык. Вот и распространение фронта ударной волны не имеет прямого отношения к эффекту Доплера, т.е. к частотной модуляцией сигнала передатчика. А Замятин находит период, фиксируемый на приемнике, между двумя фронтами ударных волн, формируемых самим движущимся источником в строго заданные моменты времени, т.е. тогда, когда фронт первой волны достигнет приемника. Ведь он прямо пишет, что «К этому моменту источник, перейдя в точку O’, создает следующий той же фазы фронт 2, который настигает удаляющийся приемник в точке B в момент t2», что явно не относится к передатчику и ниже я на примере покажу, что фаза именно у передатчика при этом может быть любой.

 

 

При этом, странно, что, когда Замятин критически анализирует другие формулы, он пишет «Тот факт, что из всех этих формул вытекает закон продольного эффекта, очевидно, не является достаточным доказательством их правильности. Можно было бы придумать много других формул, которые бы при условии Q1=Q2=0 стали бы сводиться к выражению (1*)». Так почему же он и свою формулу не подверг сомнению по этой же причине. Тем более, как видно из текста, Замятин даже проводил эксперименты по проверке эффекта Доплера. Но, почему же он не провел простейший эксперимент по выявлению различий в результатах, получаемых по разным формулам (результаты сравнения я дам ниже), а занялся сложным экспериментом с вращающимся на диске передатчиком звуковых волн для поиска мифического поперечного эффекта Доплера, который получался в его формуле. А вот, если бы он провел обычные эксперименты для общего эффекта Доплера, то получил бы, как будет показано далее, результаты по своей формуле лучше, чем дает формула Лоренца.

 

 

Но, надо отдать должное Замятину. Ведь его формула (6*) действительно просто фантастическая, т.к. она эквивалентна его формуле через углы альфа, один из которых берется для источника из прошлого времени, а другой для приемника из будущего времени. И вот это для меня является фантастикой, т.к. я никак не могу понять, как положение приемника в будущем времени может повлиять на принимаемый им сигнал в настоящем времени. Неужели и здесь процессом распространения волн управляет божественный принцип наименьшего действия, где движение в настоящем времени подчиняется заданному положению в будущем времени. Но, давайте обратимся к конкретному примеру расчета эффекта Доплера по классической формуле Лоренца (2), Юдина (3) и по полученной Замятиным формуле (6*), а потом рассмотрим и выводы Акимова и Купряева. Для этого немного видоизменим рисунок Замятина. Пусть у нас в какой то момент времени в точке О передатчик, который движется на источнике со скоростью V2, начинает генерировать сигнал определенной частоты, например, v0=0,2 Гц с нулевой фазой, который настигает приемник, который движется со скоростью V1, в точке 1. Эта точка находиться на расстоянии 100 м от точки О и ее ордината равна 50 м. Если мы примем, что скорость распространения сигнала Vs =20 м/с, то, следовательно, с момента, когда была начата генерация сигнала в точке О, прошло время dt=5 с. Примем, что у нас V1=6 м/с, а V2=10 м/с. А, т.к., когда приемник начал принимать сигнал от передатчика, источник переместился, то в данный момент времени t1 он находится в точке 2.

 

 

 

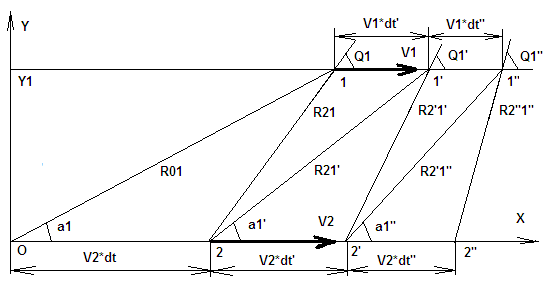
Рис. П1-1. Иллюстрация к расчету эффекта Доплера по времени распространения фронта волны.

 

Итак, передатчик будет генерировать колебания с частотой 0,2 Гц, а т.к. эта частота передатчика будет промодулирована (частотная модуляция) движущимся источником, то в направлении на точку 1 сигнал будет распространяться с частотой v(01) = v0 / (1-b2*cos(a1)) = 0,3527 Гц и если бы приемник был  неподвижный то именно эту частоту он бы и зафиксировал. А при движущемся приемнике она будет приниматься в точке 1 как частота v(1) = v(01) * (1-b1*cos(a1))= 0,2611 Гц. При этом непосредственно мгновенную частоту принимаемого сигнала в момент, когда приемник будет находиться в точке 1, зафиксировать экспериментально мы не можем, т.к. для этого необходимо иметь хотя бы один период синусоидальных колебаний. Т.е. мы можем зафиксировать частоту только в интервале времени около точки 1, например, начав фиксацию сигнала за пол периода колебаний до момента времени, когда приемник будет в точке 1 и закончив спустя пол периода колебания после этого момента.

 

 

Поэтому и в нашем расчете какой-то мгновенной частоты приема, при использовании одного угла отражающего направление распространения сигнала от источника к приемнику, мы можем только приблизительно задать этот средний для принимаемого периода колебаний угол. Например, для первого принимаемого периода сигнала передатчика (см. рис. П1-1) это будет положение между моментами времени, когда приемник находился в точках 1 и 1', и надо в расчетной формуле использовать угол a1 не в направлении на точки 1 и 1', а на середину отрезка между ними и из точки находящейся посредине между точками О и 2. Наглядно эту неопределенность, связанную с необходимостью принять хотя бы один период колебаний демонстрирует рис. П1-2. Если мы приняли часть синусоидальных сигналов S1 и S2 на участке 1-2 или на участке 2-3 и при этом у нас, естественно, не будет горизонтальной линии, чтобы знать увеличивается амплитуда или уменьшается от нулевого значения, то мы, как Вы догадываетесь, не только не сможем определить частоту принимаемого сигнала, но и не сможем сказать у какого сигнала S1 или S2 частота будет больше.    

 

 

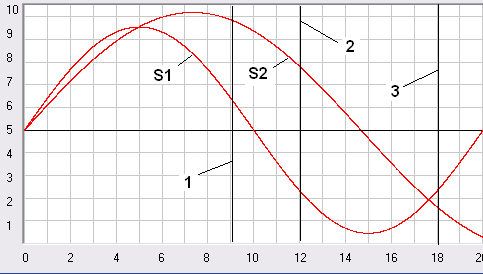
Рис. П1-2. Сравнение частот двух принимаемых сигналов при их частичном приеме.

 

 

При этом для заданной нами в примере частоты колебаний сигнала передатчика v0=0,2 Гц, которая будет приниматься в точке 1 с частотой v(1)= 0,2611 Гц, период которой T(1)= 1/v(1) = 3,83 с, получается очень большая ошибка в определении частоты принимаемого сигнала, т.к. за это время (3,83 с) от начала периода и до конца у нас очень сильно изменятся углы a1 и Q1. Но, если мы будем использовать в рассматриваемом примере высокую частоту, чтобы сделать условный период колебаний очень маленьким и максимально уменьшить погрешность, как теоретического, так и практического определения мгновенной частоты, то трудно будет анализировать ошибку использования формул для эффекта Доплера. К тому же нам надо сделать наглядным смещение фазы сигнала при рассмотрении вывода формулы Замятиным, поэтому мною специально частота принята такой маленькой.

 

 

А то, что при проведении натурных экспериментов мы никак не можем точно вычислить мгновенную частоту принимаемых сигналов, если у нас изменяются скорости V1 и V2 или углы a1 и Q1, то это данность от которой никуда не уйти. И в таких случаях, говоря о частоте принимаемых сигналов, мы просто всегда должны указывать погрешность, с которой она определена. Но сейчас в нашем примере мы рассматриваем чисто теоретический вопрос, поэтому, и частоту принимаемого сигнала и его фазу мы определяем чисто теоретически. А в этом случае мы уверены, что у нас никаких погрешностей нет, кроме известных нам особенностей связанных с временем приема хотя бы одного периода сигнала, и мы по данным наших расчетов можем точно сопоставлять результаты, получающиеся по разным формулам.

 

 

Так вот, за время dt равное 5 с, сигнал передатчика, выйдя из точки О достигнет точки 1, т.е. в этой точке будет принята нулевая фаза сигнала. А вот сам передатчик за это время, придя в точку 2, сделает ровно одно колебание и у нас в этот момент времени будет начата передача второго сигнала (продолжение первого) с той же нулевой фазой или можно сказать, что будет передан конец первого периода колебаний. Но для следующих моментов времени в точках 2' и 2'' это будет уже не так. До точки 2' передатчик сделает 0,2*(5+3,907)= 1,7814 колебания, а до точки 2'' он сделает 0,2*(5+3,907+3,208)= 2,423 колебания, поэтому утверждение Замятина о том, что в его выводе будет сохраняться фаза передаваемого сигнала, не верно. Да, вообще-то, Замятин и не пишет именно о сигнале. Он кругом говорит о фронте волны, т.е. ведет речь о распространении именно фронта ударной волны, поэтому, не будем больше придираться к его выводу формулы (6*), а давайте просто посмотрим, что она дает.

 

 

Для этого, давайте, теперь определим, где будет находиться приемник (точка 1’), когда до него дойдет сигнал из точки 2, где сейчас находится источник, а затем определим, где будет находиться приемник (точка 1’’), когда до него дойдет сигнал от источника из точки 2’. Т.е. давайте повторим на численном примере расчеты Замятина, а для наглядности рассчитаем не одну точку в будущем, как у него, а две. Все эти расчеты можно выполнить и на программе Dopler4 при проведении вычислительного эксперимента решая численным методом уравнения математической модели эффекта Доплера, но я их дам здесь в поэтапном аналитическом решении, т.е. так, как я их выполнял до написания программы. Для определения времени dt’, которое необходимо для распространения сигнала из точки 2 в точку 1’, составим уравнение

 

R21’^2 = Y1^2 + (X1 - X2 + V1*dt’)^2

 

С учетом того, что R21’ = Vs * dt’, получим квадратное уравнение относительно dt’. Решив его, найдем, что один из корней равен 3,907, т.е. это и будет наше время dt’ за которое приемник переместится из точки 1 в точку 1’, а сигнал от источника из точки 2 настигнет его. Т.к. у нас было X1=86,6 м, а X2=50 м, то мы получим в момент времени t2 следующие координаты приемника и источника

 

X1’ = X1 + V1* dt’ = 110,04 м

X2’ = X2 + V2* dt’ = 89,07 м

 

Аналогично произведем расчет и для определения координат точек X1’’ и X2’’ через промежуток времени dt’’ прошедший с момента времени t2. У нас получиться dt’’=3,208 с и координаты приемника и источника станут

 

X1’’ = X1’ + V1* dt’’ = 129,29 м

X2’’ = X2’ + V2* dt’’ = 121,15 м

 

Давайте, теперь сравним результаты, получающиеся по формуле Лоренца (2), Юдина (3) и по формуле Замятина (6*). Для этого нам потребуются для формул (2) и (6*) углы Q1, а для формулы (3) углы а1.

 

a1 =   arctg (Y1 / X1) =            30

a1’ =  arctg (Y1 / (X1’ – X2)) = 39,79

a1’’ = arctg (Y1 / (X1’’ – X2’)) = 51,19

Q1 =   arctg (Y1 / (X1 – X2)) = 53,8

Q1’ =  arctg (Y1 / (X1’ – X2’)) = 67,25

Q1’’ = arctg (Y1 / (X1’’ – X2’’)) = 80,79

 

 

По моей формуле (3), с учетом наших обозначений и того, что b1= V1/Vs , b2= V2/Vs и того, что скорости источника и приемника параллельны, у нас углы между векторами этих скоростей и радиус вектором для источника и приемника будут одинаковые, частота сигнала, принимаемого приемником, когда он будет находиться в точках 1, 1’ и 1’’ будет

 

v1 = v0 * (1 – b1 * cos(a1)) / (1 – b2 * cos(a1)) = 1,3055 * v0

v1’ = v0 * (1 – b1 * cos(a1’)) / (1 – b2 * cos(a1’)) = 1,2496 * v0

v1’’ = v0 * (1 – b1 * cos(a1’’)) / (1 – b2 * cos(a1’’)) = 1,1825 * v0

 

А по формуле Лоренца (2) мы получим

 

v1 = v0 * (1 – b1 * cos(Q1)) / (1 – b2 * cos(Q1)) = 1,1676 * v0

v1’ = v0 * (1 – b1 * cos(Q1’)) / (1 – b2 * cos(Q1’)) = 1,0959 * v0

v1’’ = v0 * (1 – b1 * cos(Q1’’)) / (1 – b2 * cos(Q1’’)) = 1,0348 * v0

 

И по формуле Замятина

 

v1= v0 * sqrt(1–b1^2*sin(Q1)^2)–b1*cos(Q1)) / sqrt(1–b2^2*sin(Q1)^2)–b2*cos(Q1))= 1,2798*v0

v1’= v0 * sqrt(1–b1^2*sin(Q1’)^2)–b1*cos(Q1’)) / sqrt(1–b2^2*sin(Q1’)^2)–b2*cos(Q1’))= 1,2177*v0

v1’’= v0 * sqrt(1–b1^2*sin(Q1’’)^2)–b1*cos(Q1’’)) / sqrt(1–b2^2*sin(Q1’’)^2)–b2*cos(Q1’’))= 1,1491*v0

 

 

Интересно отметить, что по формулам Замятина через углы a1, т.е. когда для текущего времени приемника вычисляется принимаемая им частота по углам, отражающим положение источника в прошлом времени, т.е. учитывается запаздывание по координатам, а положение приемника в будущем времени, получаются те же результаты, как и по его формуле (6*), когда углы и для приемника и для источника вычислялись нами выше по их положению в текущий момент времени.

 

v1= v0 * sqrt(1 – 2*b1*cos(a1’)^2) + b1^2) / sqrt(1 – 2*b2*cos(a1) + b2^2)= 1,2799*v0

v1’= v0 * sqrt(1 – 2*b1*cos(a1’’)^2) + b1^2) / sqrt(1 – 2*b2*cos(a1’) + b2^2)= 1,2176*v0

 

 

Таким образом, мы видим, что при принятых нами значениях скоростей, результаты по разным формулам получаются существенно разными и эту разницу в полученных нами данных легко зафиксировать в простейшем эксперименте. Ведь, если увеличить наши скорости из примера в 15 раз, то мы получим данные для эксперимента с распространением звука, а осуществить такой эксперимент при существующем уровне развития техники не составляет никакой трудности. Поэтому, мне не понятны нескончаемые споры в последнее время о том, какая из этих двух формул (Лоренца или Замятина) правильная для эффекта Доплера (естественно моя формула, т.е. Юдина). При этом, формула Замятина, хоть и похожа на формулу для эффекта Доплера, но ее вывод, сделанный Замятиным, говорит о том, что она получена явно для другого эффекта. Но, давайте до проведения натурных экспериментов, проверим формулы Лоренца, Юдина и Замятина по данным нашего расчета.

 

 

Так вот, как я писал выше, когда источник был в точке О, передатчик начал излучать сигнал с частотой 0,2 Гц и через 5 с, когда источник прибывал в точку 2, передатчик сделав одно колебание опять начинал излучать сигнал для следующего периода колебаний. А приемник начал принимать сигнал от первого периода колебаний в точке 1 и закончил принимать в точке 1', и между этими двумя положениями приемника прошло время dt’= 3,907 с, т.е. на этом интервале времени частота принимаемого сигнала получится v(11')= 1/3,907= 0,2559 Гц. Давайте теперь посмотрим какая частота на этом интервале времени, т.е., грубо говоря, в точке расположенной посередине между точками 1 и 1' получается по данным, которые мы получили выше, по нашим трем формулам, если ее вычислить как среднюю частоту между частотами рассчитанными для точек 1 и 1' и сравним ее с наблюдаемым значением 0,2559 Гц.

 

v(11')= 0,2*(1,3055+1,2496)/2= 0,2555 Гц       (Юдин)

v(11')= 0,2*(1,1676+1,0959)/2= 0,2264 Гц       (Лоренц)

v(11')= 0,2*(1,2798+1,2177)/2= 0,2498 Гц       (Замятин)

 

Как видим, формула Лоренца дает очень плохой результат, а формула Замятина, хотя и получена не для эффекта Доплера, но дает результат гораздо лучше. Но почти идеальный результат получается только по моей формуле и, таким образом, вопрос о том, какая формула для общего эффекта Доплера является правильной можно считать закрытым.

 

 

Но выше я упомянул еще о двух выводах формул для эффекта Доплера – Акимова и Купряева, одна из которых повторяет формулу Замятина, а другая формулу Лоренца, но они получены только для неподвижного приемника и поэтому менее ценны, чем общие формулы Замятина (6*) и Лоренца (2). Но давайте рассмотрим то, как эти авторы получили их, т.к. возможно, что они их выводили действительно для эффекта Доплера, в отличие от Замятина, и тогда интересно будет посмотреть как это им удалось сделать для движущегося источника, т.к. я не смог по эффективным скоростям получить аналитически правильную формулу даже для продольного эффекта Доплера при движении источника (3-1). А начнем в исторической последовательности с Акимова. В своей работе [3] он пишет

 

 «На рис. 1а вычерчен застывший в произвольный момент динамический процесс распространения волн. На одной из окружностей — неважно какой, поскольку все треугольники 0АВ будут подобными, — выбрана точка А. Стороны треугольника 0А и 0В соответствуют скоростям v и c; нужно по двум сторонам треугольника 0АВ найти третью — АВ. Для решения этой задачи треугольник 0АВ достраиваем до прямоугольного 0АС, как показано на рис. 1б. Из последнего чертежа находим отрезки a = v sin θ и b = v cos θ. По теореме Пифагора составляем равенство:

                                                             

Если в последнее выражение подставить значения a и b, получим искомую скорость c' :

                                                   .     (3)

Умножая обе части равенства (3) на период колебаний Т, получаем изменившуюся за счет эффекта Доплера длину волны λ', которую удобно выразить через параметр β:

                                             .    (4)

Формула (4) есть истинное, абсолютно точное выражение, описывающее эффект Доплера для любых значений параметра β.» (здесь у автора β= v/c).

 

Рис. П1-3. Чертеж (а) представляет собой застывшее изображение процесса распространения волн при движущемся источнике колебаний ( i ). Пока волновой фронт, испущенный из точки 0, дойдет до точки А, источник колебаний i окажется в точке В. Чтобы найти выражения для векторной суммы векторов v и c, на чертеже (б) показан вспомогательный прямоугольный треугольник (воспроизведено из работы [3], где это рис. 1).

 

Да формула у Акимова получилась та же самая, что и у Замятина (только для неподвижного приемника), но в выводе у Замятина хотя бы скорость распространения сигнала была одинаковой во всех направлениях, а у Акимова явно видно, что вывод притянут за уши, т.к. у него, почему то, скорости c и c’ разные, хотя он пишет в подписи к рисунку, что, как и Замятин, рассматривает движение волнового фронта. Но у этого фронта при распространении в какой-то среде может быть только одна скорость распространения, а не разные в разных направлениях при отсутствии движения среды. К тому же, у Акимова мы видим и еще один математический фокус, т.к. в завуалированном виде Акимов здесь демонстрирует в действии ту же фантастическую машину времени, что и Замятин. Ведь скорости c и V у него относятся к настоящему времени, а скорость c’ к будущему времени. Да, чисто с математической точки зрения сложение векторов выполнено правильно, но в нашем случае эти вектора нельзя складывать, т.к. у нас это не отвлеченные вектора, а векторы конкретных скоростей. А в таком случае мы можем складывать векторно скорости тела движущегося одновременно по двум координатам, чтобы найти суммарный вектор скорости, который позволит вычислить координаты точки, куда придет тело за то же время, что и двигаясь отдельно по каждой из координат, т.е. мы рассматриваем движение в одном и том же времени. А у Акимова получается, что из точки В в точку А тело (фронт волны) движется уже в будущем времени, когда движение со скоростями c и V уже закончилось, т.е. ни о каком векторном сложении скоростей тут не может быть и речи.

 

 

И его утверждение о том, что частота v0 (у него используется эквивалентная ей длина волны λ) является частотой передатчика, которая с учетом эффекта Доплера по его формуле, учитывающей движение источника сигнала, получается для приемника другой, тоже является ошибочным. Ведь у Акимова за v0 берется частота сигнала при его движении из точки 0 в точку А (то же самое и у Купряева), но это не частота передатчика, которая должна согласно эффекту Доплера при движении источника сигнала приниматься на приемнике уже другой величиной. Это частота сигнала, распространяющегося в направлении на приемник, т.е. из точки 0 в точку А, которая является частотой сигнала передатчика уже промодулированной движением источника и определится она согласно формуле Доплера как v(0А) = v0 / (1-V*cos(Q)/Vs). И в том случае, если у нас приемник неподвижен, то он эту частоту и будет принимать. А, если говорить о формуле Акимова (4*), то этой частоте у него соответствует длина волны λ, но у Акимова она, почему-то, считается исходной частотой передатчика, которую надо опять подвергнуть преобразованиям согласно его формуле, т.е. промодулировать еще раз. Но в таком случае я вообще затрудняюсь сказать, что он определяет как λ'. Таким образом, вывод формулы для эффекта Доплера у Акимова не только не имеет никакого отношения к эффекту Доплера, но и выполнен, мягко говоря, антинаучными методами.

 

 

А теперь давайте посмотрим, что же придумал Купряев, чтобы защитить от Акимова (Замятина) формулу Лоренца. Проанализируем только начало его вывода формулы для эффекта Доплера, т.к. ясно, что дальше нечего и смотреть. В работе [2] Купряев пишет

 

«Излучаемые источником сферические волны распространяются в пространстве со скоростью света c. Какой период tau “колебания” волн зафиксирует неподвижный наблюдатель P ?

Обозначим через Q угол между направлением распространения волны и положительной осью X в системе отсчета S. Пусть начало колебания источника, приходится на момент времени t=0, когда источник находится в начале координат системы отсчета S. После завершения полного цикла колебания (периода T), источник переместится в точку с координатами (VT,0,0) и начинает излучать вторую волну. Волны, разделенные промежутком времени T и расстоянием VT, будут, таким образом, распространяться в неподвижном пространстве как две расширяющиеся сферы: с центром в начале координат (0,0,0) и с центром в точке с координатами (VT,0,0). Дальнейшая судьба источника нас не интересует.

 

Пусть первая волна, испущенная источником в момент времени t=0, достигает наблюдателя в момент времени NT в точке с координатами (N*c*T*cosQ, 0, N*c*T*sinQ), где N – число длин волн (необязательно целых), укладываемых на этом расстоянии. (Источник к этому моменту времени может находиться где угодно, например, на расстоянии NVT от начала координат S и совершенно не интересует.) Радиус первой волны (с центром в начале координат (0,0,0)) в момент времени NT составляет NcT.

 

Вторая волна, испущенная источником в момент времени t=T, очевидно, имеет радиус (N-1)*c*T  с центром в точке с координатами (VT,0,0) и достигает наблюдателя в момент времени NT+tau. Радиус второй волны увеличивается при этом на величину c*tau. Нужно найти tau.»

 

 

Рис. П1-4. Схема к расчету эффекта Доплера при неподвижном приемнике Р и движущимся со скоростью V источнике (воспроизведено из работы [2]).

 

 

Тут мы видим, Купряев не стал совершать ошибку Замятина и вычислять время движения первого фронта мифической волны до приемника, чтобы через это время началось распространение второго фронта или Акимова, у которого используется мифическая скорость с’ для движения второго фронта волны, а рассматривает движение второго фронта волны ровно после одного колебания с той же скоростью. Только использует при этом не период колебания передатчика, как надо было сделать, а использует период уже промодулированного сигнала. А вот дальше опять начинается фантастика с машиной времени, но не явная, как у Замятина и Акимова, а в виде утверждения Купряева о том, что расстояние между точками i и Р у нас будет (N-1)*c*T + tau*с. Уж хоть бы написал, что на время tau увеличится период N колебаний, и то было бы больше похоже на правду. Но, нам на этом пути движения волны не известны ни период колебания этих волн, ни количество волн, которое уложится на этом отрезке, и по этому здесь нет никакого решения. А вот при гипотезе Купряева о том, что у нас между точками О и Р и точками i и Р будет одинаковое количество колебаний, но с разным набором длин волн, есть решение, но оно является полным произволом.

 

 

При этом если бы речь у нас шла о теоретическом выводе какого-то закона, который потом мы будем экспериментально проверять по эффектам, которые следуют из этого закона, то в данном случае возможны различные гипотезы. А здесь у нас рассматривается теоретическое доказательство справедливости уже существующего закона для расчета эффекта Доплера, поэтому, мы можем использовать только бесспорные утверждения. А в данном случае за время tau при разных частоте передатчика, скорости источника и угле Q у нас может быть произвольное количество колебаний. Единственный случай, который здесь мог бы представлять интерес, это когда между точками O и P будет укладываться одна длина волны, т.е. при N=1. Тогда у нас расстояние между вторым положением источника и приемника будет (N-1)*c*T + tau*с =0 + tau*с, но в этом случае нельзя принять, что Q1=Q, т.к. это можно сделать только при очень больших N. Да и в этом случае предположение, что за время tau будет сделано одно колебание тоже будет ошибочным. Поэтому, весь вывод Купряева построенный на его фантастическом утверждении является ошибочным и дальше можно не читать, т.к. там пошла голая математика, где он подобно тому, как мы находили dt в численном примере рассматривая формулу Замятина, находит tau, а потом, используя ее, находит выражение для частоты принимаемого сигнала (формула 12*), которую умножает на бесконечность, а потом делит на бесконечность и получает формулу Лоренца.

 

 

Давайте лучше, используя эту формулу Лоренца, которой должны соответствовать все преобразования Купряева, проверим его фантастическое заявление. Для этого используем данные нашего расчета по рис. П1-1. У нас там было ОР=100 м, Vs =20 м/с, V=10 м/с, Q=30 градусов, XP=86,6 м, а YP=50 м. А вот частоту давайте возьмем побольше, чтобы N не было равно 1. Пусть частота сигнала распространяющегося из точки О в точку Р будет v(0P)=1 Гц. Тогда N=100/20/1=5, а частота передатчика (согласно формуле Лоренца) будет v0 = v(0P) * (1 – V * cos(Q)/Vs ) = 0,567 Гц. Теперь найдем угол Q1 и расстояние между точками i и P. Q1=arctg(50/76)=33,13 градуса. iP=YP/sin(Q1)=91,48 м. А теперь, используя заявление Купряева, найдем tau=(iP – (N-1)*T*Vs) / Vs = 0,57 с. Далее найдем (согласно формуле Лоренца) частоту сигнала, который будет распространяться от передатчика из точки i в точку P, т.е. v(iP) = v0 / (1 – V * cos(Q1)/ Vs) = 0,975 Гц. Следовательно, период колебаний этого сигнала будет T(iP)= 1/v(iP)= 1,025 с, что никак не соответствует заявлению Купрява о том, что он будет равен tau, т.е. 0,57 с. Но, если бы даже он сделал более правдоподобное заявление, что на время tau увеличится период N колебаний, то и тогда ответ бы был не правильным, т.к. тогда T(iP)= ((N-1)*T(OP)+tau)/N = 0,915, что тоже не равно 1,025. Да, далее Купряев пишет, что углы Q и Q1 будут примерно равны при очень больших N, но как бы не было велико N, его заявление всегда будет оставаться ошибочным, кроме случая, когда N равно бесконечности, т.е. когда период колебаний будет равен нулю и не будет вообще никаких колебаний, а будет только деление бесконечности на бесконечность и бесконечная благодать.

 

 

Но, если бы даже Купряев правильно определил отношение периодов принимаемого сигнала при его движении из точки О и из точки i, то и в этом случае эффект Доплера у него был бы рассчитан не правильно из за той же ошибки, что была и у Акимова. Ведь в эффекте Доплера нам надо найти изменение частоты именно передатчика, но Купряев, зачем-то, используя преобразования Галилея, находит частоту источника в движущейся системе отсчета и приходит к выводу, что она будет такой же, как и в покоящейся системе координат. Но, это частота самого передатчика при этом не изменится, а частота волн распространяющихся в разных направлениях из-за частотной модуляции при движении источника будет разной. А он, как и Акимов, дает формулу для вычисления величины на которую изменится период сигнала передатчика, уже промодулированный движением источника при его распространении из точки О, по сравнению с периодом сигнала передатчика, промодулированного движением источника, при его распространении из точки i.

 

 

А вот если бы Акимов и Купряев ясно себе представляли, что эффект Доплера это частотная модуляция сигнала передатчика движущимся источником с последующей частотной модуляцией этого (уже промодулированного источником) сигнала еще и приемником, то они не сделали бы этой ошибки, а именно – не принимали бы за исходный сигнал передатчика сигнал уже промодулированный источником. А Купряев ясно пишет, что у него период T= Ti, т.е. он тоже принимает, что из точки О в точку P у него сигнал распространяется именно с частотой передатчика, но на самом деле из точки О в точку P будут распространяться волны с частотой v(ОP) = v0 / (1 – V*cosQ/ Vs), а не с частотой передатчика, которая будет v0. Таким образом, период этих колебаний будет не 1/v0, а 1/v(ОP) и, следовательно, вторая волна у него начнет распространяться из точки i, когда передатчик с частотой v0 еще не успеет сделать целое колебание. Более того, т.к. у него получилась формула для частоты сигнала принимаемого из точки i в функции от частоты сигнала принимаемого из точки О, то его формула в функции от частоты передатчика должна выглядеть так, как дано ниже, а это точно не формула Лоренца (2), где v0 это именно частота передатчика. И получается, что и Купряев зачем то, как и Акимов, опять подверг преобразованиям (согласно формуле Лоренца) частоту сигнала распространяющегося из точки О в точку P.

 

v(iP) = v(ОP) * (1 – V*cos(Q)/Vs) = v0 * (1 – V*cos(Q)/Vs)^2 

 

 

Таким образом, ничего интересного с точки зрения идей, как получить чисто теоретически формулу для эффекта Доплера с использованием эффективных скоростей, как в формуле (3-1), нам этот разбор ошибок Замятина, Купряева и Акимова не дал. Поэтому, я пока остановлюсь на созданном мною имитаторе (3-2), а вот возможно, что кто-то из читателей попробует получить чисто теоретически формулу хотя бы для продольного эффекта Доплера с использованием эффективных скоростей, которые при этом автоматически учтут аберрационные поправки в этом эффекте.

 

 

 

 

 

 

                                                                                                                                        ПРИЛОЖЕНИЕ 2

 

Отличие моделей от имитаторов и натурного эксперимента от вычислительного.

 

 

Под моделью следует понимать копию объекта, находящуюся с ним в определенном объективном соответствии, способную замещать его на определенных этапах познания и практической деятельности человека и дающую при ее исследовании информацию о самом моделируемом объекте, т.е. об оригинале. При этом под объектом в смысле объективной реальности следует понимать различные системы: механические, физические, биологические, социально-экономические и т.д., а под системой следует понимать ограниченное множество элементов объединенных причинно-следственными и функциональными связями, позволяющими ей функционировать определенным образом. И, если охарактеризовать объект с точки зрения теории отражения, то он подвергается внутренним и внешним воздействиям и реагирует на них изменением своего состояния в виде различных показателей работы (показателей функционирования).

 

Но не надо путать модели с имитаторами (симуляторами), которые тоже являются копиями объекта, но в отличие от моделей, они не могут замещать объект при его познании и, следовательно, не могут дать новой информации о самом объекте, а могут только выдать уже известную информацию, но в другом виде. Таким образом, имитаторы могут быть использованы только для оптимизации параметров систем и только в тех условиях, при которых они были получены. Т.е. с помощью моделей можно проводить как синтез систем, так и их анализ, а с помощью имитаторов, только синтез. Это объясняется тем, что, например, математические имитаторы не раскрывают сущности явлений, т.е. их взаимную внутреннюю связь, а только выдают формальный результат, который должен получиться при функционировании системы. А вот математические модели отражают объективное влияние параметров системы на показатели ее функционирования вследствие внутренней логики объекта. Т.е. в отличие от моделей, где отражена и форма и содержание, в имитаторах, в общем случае, отражена только форма. При этом наличие в математических моделях логической структуры позволяет не только прогнозировать показатели работы системы, но и экстраполировать выводы, вытекающие из структуры модели, на структуру самого объекта.

 

 

Рис. П2-1. Классификация моделей и имитаторов.

 

При этом как модели, так и имитаторы (симуляторы) разделяются на материальные и идеальные. Материальные модели и имитаторы систем состоят из вещественных элементов, природа которых у моделей, как правило, одинакова с природой оригинала и реализуются они на основе теории подобия. А идеальные модели и имитаторы, в отличие от материальных, состоят не из вещественных элементов, а свойства оригинала описаны в них с помощью цифр, функций, логических построений и образов предметов и ситуаций. При этом идеальные как модели, так и имитаторы, делятся на количественные и качественные. И хотя, человеческий мозг при принятии решений использует воображаемую модель, в которой имеются как качественные параметры, так и количественные, одновременно и которые закодированы в мозгу человека одним и тем же индивидуальным кодом, мы пока еще не научились хорошо делать ни качественные, ни смешанные модели. 

 

Количественные же идеальные модели - это математические модели (ММ), построенные на принципах стандартной логики и в их основе всегда лежат законы. Если в их основе заложены объективные законы, т.е. законы Природы, то данная модель всегда обладает прогностической функцией, т.е. с помощью нее мы можем уверенно прогнозировать будущее. Если же в ММ имеются как объективные, так и субъективные законы, т.е. законы поведения человека или законы налогового кодекса, то прогнозировать будущее с помощью таких ММ можно только с какой-то вероятностью в расчете на то, что эти законы либо не будут меняться, либо будут меняться по известным нам правилам.

 

Но все известные нам законы Природы не являются абсолютной истиной и, следовательно, ММ могут состоять не только из законов в строгом их понимании, но и из более простых математических зависимостей, отражающих определенным образом взаимосвязь различных явлений на доступном нам на сегодняшний день уровне. При этом в основе ММ должны лежать все же законы, которые вместе с этими простейшими зависимостями, т.е. математическими имитаторами (МИ), должны быть логически все объединены в единую систему. И чем больший процент математических формул, входящих в ММ будут составлять законы, а не МИ, которые чаще всего являются просто различными аппроксимациями экспериментальных данных, тем достовернее будет прогноз на будущее. Таким образом, любая ММ отражает условность уровня познания достигнутого ее создателем и, следовательно, она обязательно должна содержать в себе способность к расширению и модификации, когда отдельные явления, не учтенные или слабо отраженные в ММ, могут быть учтены при дальнейшей работе с нею, если это потребуется для достижения другой цели операции. При этом переделывается не вся ММ, а только один ее элемент, а у МИ чаще всего приходится переделывать все математическое выражение.

 

Но при этом надо всегда помнить и о том, что по большому счету математическое описание явлений Природы это в любом случае только математическая аппроксимация этих явлений в тех понятиях, которые выработало человечество. Ведь все законы Природы появились именно как аппроксимация экспериментальных данных, но только не формальная аппроксимация, а с привлечением логики. При этом, какой бы удачной ни была эта аппроксимация, но это в любом случае только наше приближение к точным законам Природы, которые могут быть построены и на таких принципах, о которых у человечества даже нет пока понимания. И уж, конечно же, Природа не обязана подчиняться придуманным нами законам, например, принципу наименьшего действия, а так же у Природы не может быть таких вещей (придуманных человечеством), как вариационное исчисление или Риманова геометрия.

 

При этом ММ ещё подразделяются на элементарные и сложные, а ММ и МИ на статические и динамические. Элементарные ММ - это формулы конкретных законов, а сложные ММ состоят из нескольких формул конкретных законов. В динамических моделях и имитаторах  воспроизводится та или иная форма движения материи, а в статических - воспроизводится образ оригинала. Иными словами, если за время проведения вычислительного эксперимента все параметры системы и внешние возмущения, действующие на нее, остаются неизменными во времени, а, следовательно, и показатели работы системы не меняются, то такие ММ и МИ будут статические, а если изменяются, то динамические. Например, закон всемирного тяготения Ньютона является элементарной статической моделью, а если мы опишем движение планет Солнечной системы с помощью этой статической элементарной модели и динамической элементарной модели ускорения масс (второй закон Ньютона), то мы будем иметь уже сложную динамическую ММ. А примером динамического МИ является, например, описание движения планет Солнечной системы Птолемеем или Кеплером. Большую массу примеров элементарных статических ММ можно привести из курса Сопромата, например, это уравнение прогиба балки, по которому можно найти прогиб, угол наклона и радиус кривизны балки в любом её сечении.

 

Но самыми распространенными идеальными моделями и имитаторами являются, конечно же, воображаемые модели и имитаторы, которые человек создает у себя в голове и они всегда  индивидуальны и отражают уровень познания и способность мыслить конкретного индивида. При этом вычислительные эксперименты на ММ проводятся с использованием стандартной логики, а воображаемые эксперименты с использованием как стандартной, так и индивидуальной логики, а последняя не предсказуема. Например, индивид может принять решение идти или ехать на красный свет светофора потому, что в прошлый раз все остановились и дали ему спокойно пройти или проехать. А в математических моделях и тем более тех, где нет индивида, например, в модели рассмотренного нами эффекта Доплера никакой субъективности быть не может, т.к. тут от индивида движение сигнала никак не зависит.

 

Природа, при проявлении тех или иных эффектов, не решает уравнения, описывающие различные явления, и не создает в зависимости от того, какое будет решение, тот или иной внешний эффект, т.е. показатель этого решения. Она просто воспроизводит эти явления и нужные эффекты проявляются сами. Поэтому все эффекты, которые могут проявиться в объекте, можно воспроизвести и с помощью численного решения уравнений, составляющих ММ объекта, когда не ищут ответы на конкретные вопросы, как при аналитическом решении, а просто воспроизводят явления Природы по этим уравнениями. А если при совместном решении этих уравнений должен проявиться тот или иной эффект, то он обязательно и проявится. И в этом смысле ММ - это заменитель Природы и каков будет ответ ММ, до проведения вычислительного эксперимента на ней, не знает даже создатель ММ.

 

А, если мы решаем аналитически уравнения ММ, описывающей то или иное явление, то мы получаем в зависимости от того, что мы ищем, ту или иную зависимость того или иного показателя функционирования системы, описывающей это явление. Например, формулы эффекта Доплера  отражают функциональную зависимость частоты принимаемого сигнала в функции от скоростей источника и приемника при заданной скорости распространения сигнала. Но ММ отличает от МИ не только то, что мы можем из ММ получить МИ, а и тем, что МИ позволяют сразу получить результат, который мы сможем получить на ММ только после проведения вычислительного эксперимента. При этом различные функциональные зависимости, т.е. МИ, не обязательно должны быть именно решением уравнений ММ, а могут быть любыми видами аппроксимаций экспериментальных данных. Хорошо, когда в этих аппроксимациях есть здравое зерно, т.е. когда их пытаются получить логически, но в принципе МИ является любое выражение, дающее сразу результат функционирования системы.

 

Иногда такие МИ получаются настолько удачными, что приобретают статус законов, как, например, это было с МИ Кеплера, но они все равно остаются по своей сути имитаторами и, если, например, в Солнечную систему залетит крупное тело, то планеты не будут подчиняться "законам" Кеплера, но будут продолжать двигаться согласно законам Ньютона. При этом Кеплер ничего не решал, а просто аппроксимировал экспериментальные данные движения одной планеты (Марса), а т.к. здесь мы имеем задачу двух тел (Марс и Солнце) то сейчас мы можем получить его МИ и как аналитическое решение ММ, описывающей движение этих двух тел. Но все его МИ отражают только какую-то отдельную функциональную зависимость (эллиптичность орбит, секторальные скорости, отношение периодов обращения), а вот ММ системы состоящей из Солнца и одной планеты одна содержит в себе сразу все эти функциональные зависимости. И даже, если ММ описывается одним дифференциальным уравнением, то его аналитическое решение может быть и для X(t) и для dX(t)/dt и точным и приближенным и общим и частным, т.е. из модели при этом можно получить множество различных МИ.

 

При этом получить МИ подобные МИ Кеплера, которые отражали бы более сложные зависимости для тел Солнечной системы, например, для смещения перигелия Меркурия (не путать с аномальным смещением перигелия Меркурия), решив уравнения ММ Солнечной системы, мы теоретически не можем, т.к. мы имеем в этом случае задачу трех тел, которая аналитически не решается. Поэтому, мы можем провести только вычислительный эксперимент на такой модели, решая эти уравнения численными методами, что стало возможно с появлением компьютеров. Хотя, например, Леверье или Ньюком и до компьютеров ухитрялись решать эту систему уравнений чисто аналитическими методами, но тоже с итерациями (они воздействия от всех остальных планет на исследуемую планету задавали как возмущающую функцию, в которой параметры орбит всех остальных планет брались как заданные). При этом мы так же не можем решить аналитически даже простейшие системы уравнений, если они содержат нелинейные дифференциальные уравнения. Но иногда нам удается (где аналитическими методами с упрощениями, а где-то вообще не известно какими методами, т.е. чисто интуитивно) все же получить решения уравнений такой ММ, которые более-менее лаконично отражают какой то показатель функционирования этой системы для того или иного явления. И одним из таких показателей функционирования системы является рассмотренный в этой статье эффект Доплера для которого различными методами, исходя из различных предпосылок, получено множество различных МИ.

 

При этом ММ воспроизводят само явление во всех его проявлениях и мы можем наблюдать развитие того или иного процесса, который нас интересует, а МИ выдают уже готовый ответ по интересующему нас процессу. Да, как частный случай, МИ могут быть аналитическим решением системы уравнений ММ, но чаще всего это просто аппроксимация экспериментальных данных, где с точки зрения математической целесообразности отражается формальное влияние различных параметров систем на их показатели функционирования. При этом, например, человек будет подбирать коэффициенты для выбранного вида аппроксимации, обрабатывая экспериментальные данные методом наименьших квадратов, а нейронная сеть при этом будет использовать свои алгоритмы и вид ее аппроксимации будет определяться количеством нейронов в одном слое и количеством слоев в этой сети. А очень часто последнее время такие МИ создаются с использованием методов многофакторного планирования, где экспериментальные данные аппроксимируются квадратичной зависимостью сразу в функции от многих параметров системы. А до этого было модным создавать МИ по принципу "черного ящика" для которого подбирались различные передаточные функции.

 

И, хотя, часто аналитическое решение уравнений, описывающих простейшие системы, позволяет производить не только синтез, но и анализ систем (т.е. как и модели), никогда нет уверенности, что этот анализ будет правильный. Ведь мы можем получить частное аналитическое решение, результаты которого нельзя распространять на всё явление, или наоборот, как я покажу ниже, общее решение не позволяет анализировать явление резонанса, которое является частным решением. Поэтому, хотя МИ, полученные аналитическим решением уравнений ММ, обладают немного и свойством проводить анализ систем и, конечно же, описывают результат функционирования системы на гораздо более качественном уровне, чем типичные имитаторы, т.е. просто аппроксимации экспериментальных данных, но все равно их следует считать именно имитаторами. Ведь какими бы качественными не были имитаторы Кеплера, но при изменении условий функционирования системы они будут совершенно не пригодны. Хотя, для большей ясности можно и акцентировать внимание на том, что речь идет об аналитическом МИ или об аппроксимационном МИ.

 

А теперь давайте немного остановимся на том, что же это такое - вычислительный эксперимент. Во-первых, само определение для слова "эксперимент" звучит в словаре Ожегова, как то же самое, что "опыт" в его 3-м значении, а 3-е значение "опыта" звучит как - "воспроизведение какого ни будь явления экспериментальным путём, создание чего ни будь нового в определённых условиях с целью исследования, испытания", т.е. мы видим, что это именно то, что нам может дать и модель (см. определение выше). При этом даже натурный эксперимент не обязательно выполнять на самом объекте и с гораздо меньшими затратами (при удовлетворительной точности данных) мы можем получить нужные результаты, проведя натурный эксперимент на материальной модели. Например, при определении аэродинамического сопротивления самолета, мы можем продувать в аэродинамической трубе не сам самолет, а его уменьшенную копию, т.е. материальную модель, используя при этом свойство масштабности. Но, гораздо больше информации и гораздо больше возможностей мы получаем, экспериментируя не с материальной моделью, а с идеальной моделью и конкретно с математической.

 

Так вот - расчетные значения мы получаем, когда по какой-то аналитической зависимости (МИ) рассчитываем интересующий нас показатель функционирования системы, а в эксперименте мы измеряем этот показатель функционирования или по приборам в натурном эксперименте или вычисляя его по каким то другим простейшим показателям функционирования системы в вычислительном эксперименте. Причем, и в натурном эксперименте мы тоже не всегда можем измерить именно интересующий нас показатель функционирования, а тоже частенько вычисляем его по показаниям других приборов. Например, среднюю скорость автомобиля в течение 2-х часов езды замерить непосредственно очень проблематично, а вычислить, разделив измеренный по спидометру путь на время езды, очень просто. Точно также и в программе Dopler мы при моделировании движения источника, приемника и волн сигнала передатчика можем замерить (зафиксировать) только моменты времени прихода начала и конца расчетного периода сигнала на приемник, а потом уже по этим моментам времени вычислить период принимаемого сигнала и его частоту.

 

При этом, как и в натурном эксперименте, мы при проведении вычислительного эксперимента на ММ, описанной множеством различных уравнений, получаем после проведения продолжительного эксперимента только один результат для заданных произвольных условий функционирования системы. А при использовании различных имитаторов мы получаем этот результат мгновенно, используя только одну формулу, но пригодную только для конкретных условий функционирования системы. При этом обращаю Ваше внимание на том, что ММ в любом случае описывает любое явление более полно, чем конкретный имитатор (даже аналитический МИ). Например, у нас есть простейшая ММ горизонтальных колебаний груза (без трения о горизонтальную поверхность) на пружине жесткостью kF при воздействии на груз внешней силы F, изменяющейся по синусоидальной зависимости с круговой частотой w.

 

m*d2X/dt2= F*sin(w*t) - kF*X

 

Аналитическое решение этого уравнения для X(t) известно

 

X(t)= Fm*(sin(w*t) - w*sin(k*t)/k) / (k^2 - w^2)

 

Здесь удельная сила Fm=F/m, а частота собственных колебаний системы k=sqrt(kF/m). Да, это очень качественный МИ, но, например, нам надо в каких то практических расчетах посмотреть как поведет себя эта система в режиме резонанса, т.е. когда k= w. К, сожалению, воспользоваться этим имитатором мы не сможем, т.к. в этом случае у нас в знаменателе получится ноль. Тогда, зная, что при k= w у нас должен наблюдаться в системе резонанс, мы ищем аналитическое решение уравнения ММ в другом виде и получаем совсем другой аналитический МИ, который и используем в этих условиях функционирования системы. А вот если бы мы не знали, что в Природе существует резонанс, то мы бы по общему решению могли сделать вывод, что такого явления как резонанс и не должно быть, т.к. общее решение не позволяет его получить.

 

X(t)= Fm*(sin(w*t) - w*t*cos(w*t)) / (2*w^2)

 

 

Да, с этой простейшей системой, используя нужное аналитическое решение ММ, мы справились, т.к. она давным-давно изучена вдоль и поперек, а в более сложных системах мы частенько даже предположить не можем какой нам надо создать МИ, чтобы пользоваться им в данных конкретных условиях функционирования системы, т.к. никогда не наблюдали систему в этих условиях. Я уже и не говорю о том, что точно решить аналитически такие системы уравнений, которые даже не включают в себя каких-то аппрокимационных МИ и не содержат логических переходов, мы практически никогда не можем. Поэтому, какой бы качественный аналитический МИ не был в нашем распоряжении он никогда не заменит нам вычислительного эксперимента на самой ММ. А при вычислительном эксперименте ММ всегда будет воспроизводить именно то явление, которое и должно наблюдаться в реальных условиях функционирования системы. Ну, а различные аппроксимационные МИ и тем более не могут сказать как поведет себя система в услових отличных от тех при которых были получены экспериментальные данные, использовавшиеся для создания МИ. Тем более, никакой МИ не может использоваться для получения новых знаний о сложной системе, хотя, иногда аналитический МИ и может сообщить нам  что-то новое о системе, но безоговорочно доверять ему никак нельзя. Таким образом, самые достоверные данные о поведении сложных систем мы можем получить только проведя вычислительный эксперимент на ММ этой системы.