МЕХАНИКА ДЛЯ КВАНТОВОЙ МЕХАНИКИ

                                   Часть 5. Математическое описание явлений Природы

                                                  …            .первая редакция 24.03.2014                                                                                  

С. Ю. Юдин          http://modsys.narod.ru .                                                                     . modsys@yandex.ru

https://googledrive.com/host/0BwnV2Ac6zvhMalpOVGktQ1Jic1U

                                                                навигация по статье

стр.1 –   история вопроса

стр.8 –  физические подходы для описания явлений Природы как систем

стр.25 – методы математического описания систем

стр.41 – особенности метода дифференциального описания систем

стр.52 – методы решения уравнений математического описания динамических систем

стр.68 – выводы

стр.69 – список литературы

                                                                       история вопроса

Вопросам, как получения уравнений описывающих явления Природы, так и методам решения этих уравнений, я уже уделял много внимания в своих работах [5, 6, 7, 14], рассматривая те или иные аспекты этих вопросов, но сейчас я решил все эти материалы объединить в одной статье. Начнем с того, что человечество всегда пыталось описать явления Природы языком математики и изобретало различные методы решения уравнений, отражающих это описание. Хотя, конечно же, первые описания были чисто качественные, например, человек мог сказать, что видел очень яркий свет. А вот, если он говорил, что видел свет, который был яркий, как 1000 Солнц, то это будет уже количественное описание, т.е. математическое, т.к. здесь появляется предмет для математики. Но не только описать на языке математики, но и чисто качественно те или иные явления Природы или искусственные системы, созданные человеком, но функционирующие по тем же законам Природы, бывает не всегда просто. Например, Архимед не смог даже качественно описать работу изобретенного им винта, т.к. тогда не существовало таких понятий, как шаг винта и т.д., а вот работу изобретенного им рычага он смог описать. При этом само математическое описание явлений Природы имеет смысл только в том случае, если мы с его использованием можем решать конкретные задачи. Например, дифференциальное описание не имеет смысла, если у нас нет методов решения этих дифференциальных уравнений.

Естественно, первыми математическими задачами были экономические задачи, например, определение площади земельного участка или раздел урожая, выраженного количественно в каких то единицах измерения, на несколько человек. А самыми первыми из известных нам методов решения задач были динамические приближённые методы, о которых говорится в папирусе Ахмеса (около ХХ века до н.э.), где излагается методика решения таких задач и, например, одна из этих задач это решение уравнения x+x/7=19. Но затем эти методы были забыты и воцарились геометрические (графические) методы решения задач и, например, теорема Пифагора доказывается именно геометрическими  методами, а Ньютон в своих Началах решал все задачи геометрическими методами даже в начале XVIII века. Но после того как в XVI веке Виет ввёл в обращение алгебраические формулы близкие к современным, а в XVII веке было вдобавок к алгебраическому исчислению введено дифференциальное и интегральное, то на фоне простоты решаемых задач сложилось впечатление о всемогуществе аналитических методов и обо всех остальных методах решения задач просто забыли.

Но методов или методик решения конкретных задач может быть много и, например, корни квадратного алгебраического уравнения мы можем найти различными методами и все они будут давать правильный результат. Жители Древней Греции, конечно же, решали эту задачу с использованием доступного им геометрического метода, т.е. с помощью циркуля и линейки, и АльХорезми тоже решал эту задачу геометрически (это задача в его сборнике №7, где он исследовал уравнение  x^2+10*x=39). Естественно, мы сейчас можем найти эти корни с использованием известного нам аналитического решения, но можем также найти их и с использованием методов многофакторного планирования, получив уравнение регрессии, которое будет давать нужный ответ. А можем и научить находить корни уравнения нейронную сеть или нейросетевой имитатор (эмулятор), у которых получится своё уравнение регрессии или, иначе говоря, алгоритм математической целесообразности, т.е. так называемый генетический алгоритм. Но в социальной форме движения материи выживает та методика, которая не только даёт нужный  результат, но и наиболее проста и удобна в её применении. Ведь, например, основным побудительным мотивом Коперника стало не стремление изменить представление о законах Природы, при замене вращения Солнца вокруг Земли на вращение Земли вокруг Солнца, а именно стремление упростить методику Птолемея, что было очень насущным социально-экономическим требованием того времени для быстрого определения капитанами кораблей их координат. И сейчас мы пользуемся теорией Коперника, хотя при этом его теория (методика) и давала результаты гораздо хуже, чем теория Птолемея, и можно с успехом и сейчас определять координаты планет по теории Птолемея.

Поэтому, сложившееся в последнее время научное мнение об аналитическом методе решения задач, как о единственно верном и возможном, является ошибочным, а, следовательно, если и численное решение и геометрическое и аналитическое все позволяют нам получить нужный результат, то мы можем применять ту методику, которая для нас более удобна. Тем более, что не во всех задачах мы можем получить точный результат. Например, в задаче Зенона с Ахиллесом и черепахой, где Зенон утверждал, что если у черепахи, которая может передвигаться со скоростью 1м/с, будет фора в 100 метров перед Ахиллесом, который бежит со скоростью 10 м/с, то он её никогда не догонит, так как когда Ахиллес пробежит 100 метров, он затратит на это 10 секунд, а черепаха за то же время  отползет на 10 метров, на преодоление которых Ахиллесу потребуется ещё 1 секунда, за которую черепаха отползет ещё на 1 метр и т. д. Да, это типичный пример численного решения задачи, т.е. с использованием многократно повторяющихся итераций, который не дает точного ответа, когда Ахиллес обгонит черепаху. Это объясняется тем, что время, за которое Ахиллес обгонит черепаху, равно 100/9=11,11111..... секунд, т.е. это число, величина которого только асимптотически приближается к некоторому значению. Но ведь и аналитическое решение этой задачи тоже не может дать точного ответа в известных единицах измерения, а только может дать ответ до какой-то заданной цифры после запятой, поэтому и численное и аналитическое решение этой задачи дадут нам одинаково верный результат при заданной точности решения и мы можем выбрать тот или иной метод решения этой задачи, который для нас более удобен.

Теперь, что касается основ описания языком математики тех или иные явления Природы, которые мы рассматриваем, как некоторые естественные системы, или описания искусственных систем, т.е. создания математических моделей этих явлений или систем, т.е. моделей этих объектов. Под математической моделью объекта следует понимать копию объекта, которая описана языком математики, и находится с ним в определенном объективном соответствии, т.е. способна замещать его на определенных этапах познания и практической деятельности человека и давать при ее исследовании информацию о самом моделируемом объекте, т.е. об оригинале. А под объектом в смысле объективной реальности следует понимать различные системы: механические, физические, биологические, социально-экономические и т.д. При этом под системой следует понимать ограниченное множество элементов объединенных причинно-следственными и функциональными связями, позволяющими ей функционировать определенным образом. Если охарактеризовать объект с точки зрения теории отражения, то он подвергается внутренним и внешним воздействиям и реагирует на них изменением своего состояния в виде различных показателей функционирования.

При этом модель не надо путать с имитатором (симулятором), который тоже является копией объекта, но в отличие от модели, он не может замещать объект при его познании и, следовательно, не может дать новой информации о самом объекте, а может только выдать уже известную информацию, но в другом виде, т.е. имитаторы могут быть использованы только для оптимизации параметров систем и только в тех условиях, при которых они были получены. Таким образом, с помощью моделей можно проводить как синтез систем, так и их анализ, а с помощью имитаторов, только синтез. Это объясняется тем, что имитаторы не раскрывают сущности явлений, т.е. их взаимную внутреннюю связь, а только с точки зрения простой математической целесообразности отражают формальное влияние различных параметров систем на их показатели функционирования или, как сейчас модно говорить, действуют по генетическому алгоритму, а модели вследствие внутренней логики объекта отражают объективное влияние параметров системы на показатели ее функционирования. Т.е. в отличие от моделей, где отражены и форма и содержание, в имитаторе отражена только форма. При этом наличие в моделях логической структуры позволяет не только прогнозировать показатели функционирования системы, но и экстраполировать выводы, вытекающие из структуры модели, на структуру самого объекта.

Это объясняется тем, что содержание моделей составляют законы Природы, а в имитаторах отражены какие-то закономерности, которые наблюдались в конкретных условиях функционирования систем. И, если условия функционирования системы изменятся, то и эти зависимости в имитаторе станут другие. Например, если мы опишем поведение планет в Солнечной системе с использованием законов Ньютона, то это будет модель системы, а, если мы опишем их поведение с использованием кинематических закономерностей, которые использовали Птолемей или Кеплер, то это будет имитатор системы. И, если теперь в нашу систему залетит астрономический объект с заметной массой, то планеты и далее будут двигаться в соответствии с законами Ньютона (только надо будет в систему добавить этот объект). А вот теория планет Птолемея, т.е. его имитатор Солнечной системы, в этом случае будет совершенно не пригоден, т.к. планеты начнут двигаться по совсем другим траекториям, т.е. в новых условиях функционирования системы кинематические зависимости получатся совсем другие. А полное название этих модели и имитатора Солнечной системы будут – математическая динамическая механическая модель системы и математический динамический механический имитатор системы. Это связано с тем, что модели и имитаторы могут быть не только идеальными, частным случаем которых являются математические модели и имитаторы, но и натуральные, например, макет самолета, продуваемый в аэродинамической трубе является натуральной моделью.

Кроме этого модели и имитаторы могут быть статические и динамические и их отличие заключается в том, что в динамических моделях и имитаторах их поведение описывается во времени, т.е. с течением времени они изменяют свои показатели функционирования. Например, если мы на упругую балку, лежащую на двух опорах, положим в средней части массивный электродвигатель, то мы сможем описать прогиб балки с использованием формул сопромата и это будет статическая модель и этот прогиб не будет изменяться со временем. Но, если мы поместим в средней части балки электродвигатель, который будет иметь дисбаланс, т.е. будет создавать дополнительную знакопеременную нагрузку, то нам надо будет описывать поведение этой системы уже с использованием динамической модели, т.к. ее прогиб будет изменяться со временем. При этом он будет сильно зависеть от соотношения частоты приложения внешней силы и частоты собственных колебаний системы, а также от инерционных свойств балки, а не только от веса электродвигателя и момента инерции сечения балки, как в случае статической модели. Но в данной статье я рассмотрю только математические динамические механические модели систем, т.е. их описание на языке математики с использованием физических законов.

Первыми, кто начал из наблюдений за Природой создавать именно физические законы, по которым в нашем представлении она функционирует, были Леонардо Да Винчи и Галилей, а до этого законам Природы приписывались правила, по которым Природа должна функционировать, исходя из логических построений Аристотеля. И, если Аристотель приходил к логическому выводу о том, что тяжелые тела должны падать быстрее, чем легкие, значит Природа должна была выполнять этот его закон. Но первым, кто системно изложил законы, которые следуют из наших наблюдений за Природой, был Ньютон. И именно после его Начал стало возможно, используя набор физических законов, решать самые разнообразные задачи механики в едином ключе. Вот только описание этих законов у Ньютона было чисто словесное, т.е. не аналитическое, и решал он все задачи опять-таки не аналитически, а геометрически, и поэтому воспользоваться этими законами в чистом виде мог только сам Ньютон.  Поэтому-то он и рассматривает в своих Началах так много различных примеров конкретных задач, которые позволили другим ученым по аналогии решать похожие задачи. Кстати, наверное, по этой же причине, т.е. из-за отсутствия четкого математического описания этих законов, Герц в своей Механике, рассматривая различные подходы для математического описания явлений Природы, не видит разницы между импульсным подходом Ньютона и силовым Эйлера.

Ну а впервые математика показала себя в полном блеске при математическом описании явлений Природы, конечно-же, в Альмагесте Птолемея, где ему удалось не только описать движения светил, которые уже наблюдались в прошлом, но и описать их движение в будущем, т.е. теперь светила стали двигаться по его законам, т.е. создавалось впечатление, что математика управляет Природой. Это являлось как бы доказательством учения Пифагора, который обожествлял числа и учил, что числа управляют миром и, следовательно, в Природе должна быть гармония чисел. Поэтому, когда Пифагор обнаружил, что отношение стороны квадрата к его диагонали не может быть выражено простым  числом, он приказал своим ученикам хранить это в тайне, т.к. он считал, что если люди об этом узнают, то мир разрушится. Да, собственно говоря, и современные математико-физики ушли не далеко от Пифагора и тоже пытаются нас всех убедить в том, что Природа должна подчиняться созданным в их больном воображении математическим конструкциям. Но у Природы свои законы, которые мы можем только в каком-то приближении описать созданными нами физическими законами, которые мы излагаем на языке математики.

И эти законы Природы мы должны получать не из свойств тех или иных математических уравнений, которым по задумке математико-физиков эти законы должны подчиняться, а "аппроксимируя" этими уравнениями экспериментальные данные, которые мы наблюдаем. При этом сам термин "аппроксимация" это приближение к точному аналитическому уравнению, которое нам желательно получить и, когда мы получаем такое уравнение, мы говорим, что получили физический закон Природы. Только не надо путать аппроксимации частных случаев функционирования систем, т.е. математические имитаторы, именно с физическими законами, которые аппроксимируют поведение систем в любых условиях функционирования систем, т.е. с математическими моделями. И здесь, при создании таких законов, самое главное, чтобы созданная с их использованием новая физическая теория не только сама стала понятна хотя бы через определенное время после ее создания, когда новые понятия и методы мышления станут общепризнанными, но и позволила сделать более понятными описываемые ее процессы. Ведь как сказал Антуан де Сент-Экзюпери "Истина - это вовсе не то, что можно убедительно доказать, это то, что делает все проще и понятнее".

Не страшно если эта теория не понятна только в начале, как, например, было с винтом Архимеда, который он не смог описать, хотя сам и понимал, как он работает. Но в то время не было таких понятий в науке и технике, которые бы позволили это сделать, а сейчас для нас это не представляет большого труда. Но сейчас появились три физические теории, которые очень плохо поддаются их логическому пониманию и через 100 лет после их создания. Это теория электромагнитного поля Максвелла, теория относительности Эйнштейна (специальная и общая) и оставшаяся без отцовства квантовая теория (квантовая механика), которую следует, пожалуй, признать самой непонятной теорией. Таким образом, эти три теории надо было по критерию простоты и понятливости давно признать ложными учениями. Но здесь мы имеем жесточайшее сопротивление математико-физиков, которые в смутное для науки время сумели прорваться к власти в науке и отстаивают теперь свою единственно верную точку зрения на законы Природы. И эта святая инквизиция в лице Академий Наук безжалостно борется со всяким инакомыслием, касающемся этих теорий (священных писаний), хотя любому здравомыслящему ученому ясно, что они ошибочны. Ведь мало того, что эти теории не понятны и через 100 лет, например, Нобелевский лауреат за работы по квантовой механике Фейнман заявил, что квантовую механику не понимает никто, но эти теории и опровергаются экспериментально, хотя официальная наука на всех углах трубит о различных экспериментальных подтверждениях этих теорий. При этом официальные ученые, во-первых, не правильно интерпретируют те экспериментальные данные, которые уже есть, а, во-вторых, не проводят новые эксперименты, которые могли бы опровергнуть эти теории.

И при этом современные математико-физики продолжают идти по стопам Пифагора и придумывают свои теории (законы), исходя из божественной веры в математику, и продолжают утверждать, что Природа должна подчинятся этим их математическим законам. Например, также, как и во времена Птолемея, когда считалось что все светила должны были двигаться только по круговым орбитам, т.к. круг это идеальная математическая фигура, и сейчас математико-физики утверждают, что все законы Природы должны подчиняться чисто математическому принципу наименьшего действия (ПНД) и именно из него и получают все физические законы, которым должна подчиняться Природа. При этом, хотя у Лагранжа и Гамильтона были различные ПНД, но они были едины в том, что и Лагранж считал, что механика представляет лишь особый класс вариационных задач, и Гамильтон считал, что механика это класс математических задач и вся разработка механики сводиться к разработке различных математических методов (поэтому Гамильтон так и нахваливал Аналитическую механику Лагранжа). А вот Ньютон [16] писал что наоборот «геометрия основывается на механической практике и есть не что иное, как та часть общей механики, в которой излагается и доказывается искусство точного измерения» (в то время математики назывались геометрами).

Таким образом, научный подход Лагранжа и Гамильтона в корне противоречит методологии познания Природы Ньютона и поэтому с приходом в физику математико-физиков развитие науки пошло вспять и все достижения, какие были достигнуты в ней, были сделаны не благодаря, например, Лагранжу и Гамильтону, а вопреки им. А первым математико-физиком, конечно же, был Лагранж, хотя официально считается, что первым теоретическим физиком был Планк, но получается, что он был, по крайней мере, 4-м после Лагранжа, Гамильтона и Вебера, а далее этих математико-физиков развелось столько, что все физики (механики) стали считаться редкими ископаемыми или, как сейчас любят говорить, альтернативщиками. Хотя и не все альтернативщики сейчас являются физиками, т.к. за 200 лет господства в науке энергетическо-геометрического подхода с Лагранжево-Гамильтоновым формализмом даже те, кто пытается устранить ошибки в теориях прославляемых официальной наукой, делают их теми же методами, что и математико-физики, т.е., по сути, и сами являются таковыми.

А сейчас я могу только констатировать, что, если бы не было Аналитической псевдомеханики Лагранжа и порожденной ею псевдомеханики Гамильтона, развитие науки могло бы пойти по правильному пути, но лавры Ньютона, которые не давали спокойно спать Лагранжу не позволили этого сделать. Снискать такой же славы, как Ньютон в математике Лагранж не мог, поэтому накинулся на механику, что он, кстати, советовал сделать и всем остальным математикам в своем письме Даламберу [20]  «Я думаю также, что шахта становится слишком глубокой и что ее придется рано или поздно бросить, если не будут открыты новые рудоносные жилы. Физика и химия представляют ныне сокровища, гораздо более блестящие и более легко эксплуатируемые; таким образом, по-видимому, все всецело обратились в эту сторону, и возможно, что места по геометрии в Академии наук сделаются когда-нибудь тем, чем являются в настоящее время кафедры арабского языка в университетах.»

Вот они (математики) и накинулись, и задушили в своих объятиях всю физику, а начали, естественно, с ее основ, т.е. с механики. Вот и я начну возрождение здравого смысла в науке именно с механики, как с основы всех естественных наук и далее изложу на примере механических задач различные подходы для описания явлений Природы. И надеюсь, что эта моя работа поможет в правильном понятии законов Природы и со временем альтернативные ученые смогут выработать общие теории, которые заменят релятивистскую и квантовую механики. А в этой статье я не буду доказывать справедливость тех или иных теорий (законов Природы), а просто покажу, как с их использованием описать различные явления Природы на языке математики.

Но прежде я бы хотел еще немного остановиться и на психологических проблемах научного познания, т.к. морально-психологический климат в научной среде, который характеризуется крайней нетерпимостью к инакомыслию, оказывает очень заметное влияние на развитие науки. И началось это не сто лет назад после создания теории относительности и квантовой механики, а гораздо раньше. Например, уже в Древней Греции и Древнем Риме огромную роль в торможении процесса познания играл именно морально-психологический климат или, как мы сейчас говорим, менталитет свободных граждан, как в обществе, так и в научной среде того времени. В то время поэзия, философия и геометрия относились к высшей сфере духа, а механику считали низшей наукой. Платон даже называл ее пошлым ремеслом. Поэтому пользоваться любыми инструментами для свободных граждан считалось не достойным занятием и только для циркуля и линейки было сделано исключение. Все законы выводились только из умозрительных заключений, сделанных при пассивном созерцании Природы и мысленных экспериментов. Например, Аристотель, создатель логики и механики, наблюдая падение различных тел, вывел закон о том, что тяжелые предметы падают быстрее. И только Галилей, проведя натурные эксперименты на созданной им лабораторной установке, доказал, что все тела падают с одинаковой скоростью.

Естественно, свободные граждане Древней Греции не стали бы заниматься никакими лабораторными установками, так как это механика, и тем более подгонкой траекторий движения планет, т.е. нахождением примерного решения, как это делал Кеплер. Математика того времени сводилась к теории чисел, причем целых и положительных, правда разрешалось использовать дробные числа и квадратные корни. Типичными задачами того времени являются задачи квадратуры круга, удвоения объёма куба и нахождение корней уравнений в радикалах. Причём, тогда даже логика решения задач в корне отличалась от современной. Надо было не доказать, что это решение верное, а наоборот надо было доказать, что все остальные решения не верны, т.к. их можно логическими рассуждениями привести к абсурду. Но сколь бы ни сильна была логика того времени, а вот задачу Зенона не смог решить и создатель логики Аристотель, т.к. геометрически эта задача не решалась, аналитического решения, которое давало ответ 100/9, тогда не было, а, численные методы тогда были под запретом.

Но любая созданная физическая теория (математическая модель системы) нуждается в подтверждении своей правоты экспериментальными данными, и для этого нам надо любой ценой замерить результат эксперимента, даже если он не выражен в целых или дробных числах. А вот это в Древней Греции не просто не понималось, но и не одобрялось и последствия такого атомистического подхода в науке могли стоить человеку не только репутации, но и жизни. Поэтому Архимед, использовавший при решении многих своих геометрических задач методы численного интегрирования (атомистический подход) боялся до конца своей жизни опубликовать этот метод, т.к. уже в то время в науке велась бескомпромиссная война с инакомыслием (вплоть до уничтожения самих ученых). И только незадолго до смерти, когда он случайно натолкнулся на труды Демокрита, которые почти все были уничтожены, и обнаружил, что Демокрит тоже пользовался численными методами интегрирования для нахождения площадей и объемов фигур, он решился изложить публично свой метод. Но и его труды постигла участь трудов Демокрита и поэтому человечеству пришлось опять заново открывать методы численного интегрирования, хотя, как я писал выше, первые задачи (XX-ый век до н.э.) человечество решало именно численными методами.

А в наше время мы узнали о трудах Архимеда, посвященных численным методам, только благодаря случаю. Бумага тогда стоила дорого и поэтому работа, где Архимед излагает численные методы решения задач, была не уничтожена, а просто с бумаги смыли чернила и написали другой текст, а сейчас под этим текстом, благодаря современным методам, удалось разглядеть первоначальный текст. А начиная с XVIII века, идет тотальное наступление аналитических методов решения задач и при этом стараются даже не вспоминать о геометрических и численных методах решения, хотя, иногда еще можно найти остатки получисленных методов решения задач. Например, в задачнике Магницкого для решения алгебраического уравнения первой степени применён метод двух ложных положений. И только благодаря изобретению компьютера сейчас опять вспомнили о численных методах, т.к. сложность решаемых задач настолько возросла, что ни один математик, зная все аналитические методы, не может их решить, не говоря уже о специалисте конкретной области знаний, которому надо не только решить эту задачу, но ещё и сформулировать её. И если при этом простая и универсальная методика решения задач с использованием численных методов будет давать удовлетворительный результат, то для большинства специалистов конкретных областей знаний можно будет без ущерба для них в 2-3 раза сократить объём изучаемых разделов математики. Но этому всячески противятся математико-физики и стараются всячески дискредитировать численные методы решения задач, продолжая утверждать, что аналитическое решение дает точный ответ, а численное приблизительный. Хотя все обстоит как раз наоборот и численное решение реальных задач дает почти точный ответ, а аналитическое приблизительный и ниже я рассмотрю этот вопрос подробно.

                                  физические подходы для описания явлений Природы

А сейчас я приведу различные подходы для описания явлений Природы на языке математики с использованием физических законов, полученных из наблюдений за Природой, а потом изложу различные методы описания явлений Природы и методы решения конкретных задач, после того как мы описали явления Природы на языке математики. И наряду с известными методами дифференциального описания, т.е. в виде дифференциальных уравнений, и конечного описания, т.е. в виде алгебраических уравнений для законов сохранения, я дам и предлагаемое мною описание в приращениях. И, хотя ранее я уже применял этот метод описания для социально-экономических систем, но я его не позиционировал, как новый универсальный метод описания поведения систем, который является аналогом дифференциального описания, поэтому я подробно остановлюсь на его особенностях. При этом методы решения задачи при дифференциальном описании могут быть как аналитические для общего решения, так и численные для частного решения, например, методом Эйлера или Рунге-Кутта, а описание в приращениях дает нам сразу и метод решения, который по своей сути является численным. И так, различные существующие подходы для описания явлений Природы с основной их характеристикой и с указанием их основных признаков таковы

Нулевой – импульсный (пространство – время – масса – импульс)      - Ньютон

Первый – силовой (пространство – время – масса – сила)                      - Эйлер

Второй – энергетический (пространство – время – масса – энергия)     - Лагранж

Третий – кинематический (пространство – время – масса)                      - Герц

Четвертый – мощностной (пространство – время – масса – мощность) - Юдин

А их рассмотрение я начну с обзора Механики Герца [17], где он рассматривает три подхода (силовой, энергетический и кинематический). Герц отмечает достоинство силового подхода, состоящее в том, что силы мы можем непосредственно ощущать, например, вес камня в руке, т.е. они нам даны в ощущениях и возникли из нашего опыта. Но, в тоже время, отмечает Герц, совершенно не понятно, что такое масса, т.к. определение Ньютона о том, что это плотность, умноженная на объем нам ни о чем не говорит, т.к. логичнее сказать, что это плотность равна массе деленной на объем. Не ясна и природа силы, т.к. формулировка о том, что это произведение ускорения на массу не ответ. А мне вот странно, почему Герц при этом, говоря о массе, ссылается на Ньютона, а, говоря о силе, дает определение Эйлера, но при этом совершенно не упоминает об Эйлере, который дал очень объективные определения пространству, времени, массе и силе. Поэтому, тут у него не должно было возникать никаких вопросов, а вопрос может возникнуть у нас – неужели и Герц не знал об Аналитической механике Эйлера, как не знают о ней все современные математико-физики.

Далее Герц приводит такой пример. Мы вращаем камень на веревке и сила натяжения веревки в соответствие со 2-ым законом Ньютона изменяет его движение так, что он движется по окружности. Но 3-ий закон требует, чтобы сила действия была равна силе противодействия, а ответ о том, что этой противодействующей силой будет центробежная сила, Герца не устраивает, т.к. сама центробежная сила тоже является следствием действия сил инерции, т.е. мы вводим здесь понятие инерции один раз как массы, а другой раз как силы. Сразу хочу заметить, что именно тут никакого противоречия нет, т.к. никакой дополнительной центробежной силы не будет, а будет только сила инерции камня старающегося сохранить прямолинейное и равномерное движение. Просто при аналитическом решении подобных задач нам удобно вводить фиктивную центробежную силу, но если мы смоделируем процесс движения камня в Декартовой системе координат по двум осям и решим дифференциальные уравнения численными методами с использованием только 2-го закона Ньютона (в интерпретации Эйлера) для прямолинейного движения, то получим тоже самое движение по окружности. Если кто-то хочет это проверить, то могут скачать мои программы Savosta, Konma и другие (вместе с исходниками).

А вот следующее замечание Герца о том, что пока нет конкретного определения силы не возможно ответить на вопрос – зависит ли сила только от координат и скоростей или зависит и от производных более высоких порядков, является очень существенным. И я в своей статье [14] посвятил этому вопросу очень много места, т.к. считаю, что сила может зависеть только от координат и скоростей, а поэтому рассмотренные мною там потенциалы Вебера и Гербера являются антинаучными, т.к. в них сила зависит и от ускорений, т.е. сила зависит от силы. А полученные мною с использованием этих потенциалов значения смещений параметров орбит планет экспериментально доказывают, что такая зависимость является искусственной, т.к. не оказывает никакого влияния на полученные результаты при различных условиях функционирования Солнечной системы. Возникает у Герца и вопрос по поводу сил притяжения от далеких звезд или сил взаимодействия между отдельными атомами. Ведь непосредственно в ощущениях они нам не даны, а, следовательно, этих сил возможно и не существует. И тут я с Герцем согласен принципиально, хотя элементарная логика подсказывает, что, конечно же, эти силы должны существовать.  

Рассмотренный выше силовой подход (также как и импульсный) формировался в науке веками, а вот энергетический подход после работ Лагранжа, Гамильтона и Гельмгольца сформировался буквально за несколько десятилетий и, как пишет Герц, «к концу 19 столетия физика отдала предпочтение другому способу мышления». И действительно, после открытия закона сохранения энергии вся физика стала сводиться только к превращениям одной энергии в другую, хотя любой учебник механики по-прежнему начинался не с энергии, а с силы. Все сущности этого подхода объединяются воедино каким ни будь вариационным интегральным принципом. Герц для примера рассматривает принцип наименьшего действия (ПНД) Гамильтона. Преимуществом данного подхода является то, что он позволяет уйти от многих процессов, которые пока еще не ясны, и скрыться за общими выражениями для энергии, а понятия о силах тут возникают уже из самих энергий. Но тут сразу же возникает первая проблема. Энергия у нас состоит из двух составляющих – потенциальной и кинетической. И если с кинетической энергией все более-менее ясно, то форма зависимости потенциальной энергии от положения нескольких тел не может быть указана в общей форме. К тому же, если принять то, что энергия это материя, то, как может материя быть отрицательной, если у нас получается отрицательная потенциальная энергия.

Другими недостатками такого подхода Герц считает то, что ПНД Гамильтона применим только к обратимым процессам, т.е. к тем, где в системах нет диссипации энергии, и к системам только с голономными связями. В качестве системы с неголономными связями Герц приводит качение шара, которое происходит с обязательным упругим проскальзыванием в пятне контакта. Ну, и, конечно же, Герц указывает на то, что ПНД предполагает у неживой Природы намерений свести интеграл к минимуму или его вариацию к нулю, т.е. достичь какой-то цели, которую она перед собою ставит и при этом ее поведение в настоящем времени должно подчиняться ее положению в будущем времени. Естественно, он указывает и на очень туманный смысл этого принципа. А, если к этому добавить, что вариационных интегральных принципов в Природе никогда не существовало, как я показал это на простейших примерах в своих работах [8, 10], то становиться ясно, что такой подход (с использованием ПНД) в физике вообще антинаучен.

А теперь рассмотрим, что же нам предлагает Герц. Он пишет «То, что мы называем обычно силой или энергией, представляют собой в нашем понимании не что иное, как действие массы и движения; однако оно не всегда может быть таким действием массы и движения, которые могут быть доказаны в грубой чувственной форме». Таким образом, у него появляются скрытые движения и скрытые массы, но он замечает, что сейчас это в науке нормальное явление и, например, силы теплоты были отнесены к скрытым движениям, а благодаря работам Гельмгольца стали официальными терминами. Т.е. он допускает наличие скрытых от нашего восприятия явлений, но они отражаются в поведении системы, т.е. в изменении ее координат. А все сущности своего подхода он отражает в своем единственном принципе, который звучит так «каждое естественное движение самостоятельной материальной системы состоит в том, что система движется с постоянной скоростью по одному из своих прямейших путей».

И тут же он переводит это на обычный язык механики и пишет «А именно это положение просто объединяет обычный закон инерции и принцип наименьшего принуждения Гаусса в одно единственное утверждение». Т.е. фактически у Герца все сводиться к кинематике с ее скоростями и ускорениями. Но нам, конечно же, более удобно использовать в своих расчетах и логических рассуждениях, и понятие ускорения, которое может использоваться как самостоятельная величина при рассмотрении кинематики, и силы, которая эквивалентна этому ускорению, но не для бестелесной точки, а для конкретного тела обладающего массой. А у него понятие силы теперь становиться просто вспомогательным и промежуточным, т.к. при этом «движение первого тела определяет вначале некоторую силу, и последняя определяет уже движение второго тела», а можно и вообще обойтись без упоминания сил.

Ну, и еще, в качестве, по моему, сомнительного преимущества своего подхода перед энергетическим Герц заявляет, что «Наш метод выражения ярко оттеняет тот факт, что метод изложения Гамильтона скрывает свои корни не в особых физических основах механики, как это обычно понимают, но что он, собственно говоря, является чисто геометрическим методом, который может быть обоснован и развит совершенно не зависимо от механики и который не находиться с ней в более тесной связи, чем любое другое используемое механикой геометрическое познание. Впрочем, математики давно уже подметили, что метод Гамильтона содержит чисто геометрические истины, и для четкого выражения последних этот метод требует своеобразной, приспособленной к нему терминологии». Это конечно хорошо, что Герц это заметил, т.к. я в своей работе [10] многократно указывал на чисто геометрический (матемаический) смысл всех интегральных вариационных принципов, но и рекомендовал именно в геометрии их и использовать, т.е. для чего они собственно и создавались.

К тому же авторы статьи [21] пишут уже об его принципе прямейшего пути так «Познавательная ценность этого принципа состоит в том, что он сводит задачи механики к проблеме геодезических линий, коренным образом геометризирует классическую динамику». Да Герц и сам, когда сравнивает свой дифференциальный вариационный принцип (Гаусса) с ПНД Эйлера-Лагранжа и ПНД Гамильтона-Остроградского, приходит к выводу о том, что они являются частными случаями его принципа. Таким образом, механика Герца является еще более геометрической, чем у Лагранжа и Гамильтона и поэтому непонятно зачем он клеймил позором механику Гамильтона, как геометрическую. Более того, авторы [21] пишут, что «В теории относительности движение планет вокруг Солнца объясняется без привлечения действующих сил при помощи представления об инерции как о фундаментальном свойстве тел. Планеты движутся аналогично телам в механике Герца по кратчайшим линиям в римановом пространстве. В этом отношение теории относительности от механики Герца состоит в том, что в первой материальные движущиеся тела определяют метрику пространства – времени, его геометрию, в то время как у Герца такое движение определяется кинематическими условиями, создаваемыми скрытыми массами системы». Т.е. механика Герца практически ничем не отличается и от геометрической ОТО, но вот самой механики в ней как-то уже и не видно, а кругом одна геометрия, геометрия и связи, связи. И, таким образом, мы видим, что хотя Герц и раскритиковал, как силовой подход Эйлера, так и энергетическо-кинематический подход Лагранжа, но его чисто геометрический подход не чуть не лучше их подходов и, более того, уводит нас еще дальше от механики к математике, чем подход Лагранжа.

Ну, а т.к. Герц не сделал анализа импульсного подхода Ньютона, перепутав его с силовым подходом Эйлера, то давайте сделаем это сами. Рассмотрение этого подхода является самым сложным, т.к. этот подход в аналитическом виде не существует, а остался в словесных формулировках данных самим Ньютоном [16]. При этом Ньютон особенно ничего не изобретал, а просто единообразно изложил в своих Началах уже существующие нечеткие словесные формулировки известных на то время принципов в механике. Но при этом огромным достижением Ньютона было то, что он при такой нечеткой формулировке своего подхода сумел решить, применяя его, такое огромное количество самых разнообразных практических задач. А свои три закона Ньютон сформулировал так

1- Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

2- Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.

3- Действию всегда есть равное и противоположное противодействие, иначе - взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

Что касается  формулировки 1-го закона Ньютона, то она воспринимается однозначно и почти точно повторяет формулировку, которую дал Галилей “…скорость, однажды сообщенная движущемуся телу, будет строго сохраняться, поскольку устранены внешние причины ускорения или замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время, как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно”. Но перевести эту формулировку 1-го закона на язык формул не возможно, т.к. она носит качественный характер. А вот, если мы этот закон сформулируем для системы тел, которые взаимодействуют между собою, но на них не действуют внешние силы, то мы получим однозначную математическую формулировку для закона сохранения количества движения системы m1*V1+m2*V2…+mi*Vi=const. А, т.к. любая система и в том числе большое тело состоит из множества отдельных масс, то можно считать, что здесь у нас центр масс тела либо покоится, либо движется равномерно и прямолинейно. Но Ньютону в словесной формулировке пришлось этот закон изложить как два отдельных следствия его трех законов. Собственно как закон сохранения количества движения и о покое центра масс системы или его равномерном и прямолинейном движении.

«следствие III - Количество движения, получаемое беря сумму количеств движения, когда они совершаются в одну сторону, и разность, когда они совершаются в противоположные стороны, не изменяется от взаимодействия тел между собою».

«следствие IV - Центр тяжести системы двух или нескольких тел от взаимодействия тел друг на друга не изменяет ни своего состояния покоя, ни движения; поэтому центр тяжести системы всех действующих друг на друга тел (при отсутствии внешних действий и препятствий) или находится в покое, или движется равномерно и прямолинейно».

А вот, что касается 2-го закона Ньютона, то мне очень даже не понятно, почему Ньютон не стал участвовать в споре сторонников Декарта, утверждавших, что мерой механической формы движения материи является количество движения (импульс, момент), т.е. произведение массы на скорость, и сторонниками Лейбница и Гюйгенса, которые утверждали, что живая сила, т.е. произведение массы на квадрат скорости. Ведь это был основной вопрос натуральной философии того времени и от того, как он будет решен, зависело и все развитие науки того времени. Но, наверное, Ньютон был ближе все-таки к практике и к финансам, чем к науке, если остался в стороне при решении такого вопроса. При этом он просто тихой сапой принял сторону сторонников Декарта и занялся только решением задач, где он, как и Эйлер, действительно был гением, т.е. он был мастером решения задач, но не ученым.

А началось в этом споре все с Галилея, который говорил о том, что количество движения пропорционально скорости и массе, а Декарт сформулировал закон сохранения количества движения, т.е. «произведения величины тела на скорость его движения» очень не удачно, но формулировка Ньютона тоже мало что проясняет, т.к. он в своем определение II пишет только, что «Количество движения есть мера такового, устанавливаемая пропорционально скорости и массе», т.е. просто повторяет слова Галилея. Таким образом, главный теоретический вопрос того времени о мере механической формы движения материи остался открытым, а Ньютон о нем даже не упомянул в своих Началах, а вот Энгельс, как философ, уделил ему очень много места в своей «Диалектике природы». Поэтому, уже в середине 18-го века Даламберу пришлось опять возвращаться к этому вопросу, чтобы логически увязать эти две меры механической формы движения материи, о чем я писал в статье [7], но и его формулировка “потерянные за элемент времени количества движения образуют систему векторов, уравновешивающихся через посредство связей системы“ не все прояснила в этом вопросе и, в конце-то концов, формально узаконила только одну меру, т.е. количество движения. 

А в связи с тем, что за меру механической формы движения Ньютон принял количество движения (импульс, момент) и изложил свой 2-ой закон не в дифференциальной форме, как мы это видим у Даламбера, где явно просматривается d(mV)/dt, а в абстрактной, то у него, беря во внимание следствие III, можно понять, что и силы измеряются произведением массы на скорость. И, чтобы хоть как-то можно было при такой расплывчатой формулировке его законов решать практические задачи, Ньютону пришлось изобретать множество различных сил с разными свойствами. Например, центростремительные силы, т.е. силы притяжения тел к центру Земли или к магниту у Ньютона проявляют себя в трех ипостасях – как абсолютная, как ускорительная и как движущая силы. А из 8-и данных им определений только два первых не относятся к силам.

Определение I – Количество материи (масса) есть мера таковой, устанавливаемая пропорционально плотности и ее объему.

Определение II - Количество движения есть мера такового, устанавливаемая пропорционально скорости и массе.

Определение III - Врожденная сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает свое состояние покоя или равномерного прямолинейного движения.

Определение IV – Приложенная сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения.

Определение V – Центростремительная сила есть та, с которую тела к некоторой точке, как к центру, отовсюду притягиваются, гонятся или как бы то ни было стремятся.

Определение VI – Абсолютная величина центростремительной силы есть мера большей или меньшей мощности самого источника ее распространения из центра в окружающее его пространство.

Определение VII – Ускорительная величина центростремительной силы есть мера, пропорциональная той скорости, которую она производит в течение данного времени.

Определение VIII - Движущая величина центростремительной силы есть мера, пропорциональная количеству движения, которое ею производится в течение данного времени.

Но без четкой математической формулировки для этих сил очень легко запутаться в этих терминах, т.к.

чисто словесные формулировки можно воспринимать очень не однозначно. Например, странно выглядит перевод Начал с латыни, сделанный Крыловым (кстати, перевод очень добросовестный),  для определения «абсолютная величина центростремительной силы», т.к. в переводе используется термин «мощность», но в те времена, когда Ньютон писал свои Начала, такого термина не могло существовать. Но, как бы ни были сложны и запутаны принципы Ньютона, но они все же позволяли решать различные практические задачи в едином ключе, а в то время это было грандиозное достижение. Да, собственно говоря, сотни страниц его Начал являются просто сборником задач, рассмотренных Ньютоном, а вся теоретическая часть его Начал уместилась у него на 31 страничке (из которых 5 страниц это пояснения переводчика текста), поэтому Герц так и критиковал его теоретическую часть.

Вообще то, к теоретической части Начал можно отнести и его III книгу «О системе мира», где он на основании экспериментальных данных и своих расчетов делает многочисленные выводы об устройстве нашего мироздания, многие из которых были просто откровением для того времени. Но уже Крылов (при переводе Начал) указывает и на многие его ошибки. Например, Ньютон делает вывод, что чем меньше планета, тем больше ее плотность, но у Луны плотность меньше чем у Земли, или он утверждает, что возмущения орбиты Юпитера, от воздействия на него Сатурна меньше, чем возмущения орбиты Сатурна от воздействия на него Юпитера, но все как раз наоборот. А утверждение Ньютона о том, что «Афелии и узлы орбит неподвижны» вообще ставит меня в тупик. Ведь, как я показал в работе [11] уже в 9-м веке в таблицах Аль Хорезми и Аль Баттани афелий Солнца (перигелий Земли) значительно сместился относительно положения у Птолемея во II-м веке н.э. (83 градуса против 65), а у авторов более поздних таблиц он смещался еще больше. Более того, Ньютон здесь же производит расчет смещения узлов Луны и приводит данные астрономов, согласно которым у Луны смещаются не только узлы, но и афелий (апогей). И совсем обескураживающим выглядит его вывод о движение афелиев внутренних планет, который он делает на той же странице, где заявляет, что «Афелии и узлы орбит неподвижны».

«Так как планеты, ближайшие к Солнцу (именно Меркурий, Венера, Земля и Марс) по малости их масс оказывают лишь малое взаимодействие друг на друга, то их афелии и узлы находятся в покое, за исключением лишь того, насколько они возмущаются Юпитером, Сатурном и высшими телами. Отсюда на основании теории тяготения, можно заключить, что их афелии должны немного продвигаться в попятном направлении по отношению к неподвижным звездам и при том в полукубическом отношении расстояний этих планет до Солнца. Так, если афелий Марса продвигается относительно звезд попятно на 33’20’’ в столетие, то афелии Земли, Венеры, Меркурия должны продвигаться попятно же на 17’40’’, 10’53’’ и 4’16’'».

Так вот, во-первых, афелии движутся не попятно, а в том же направлении, во-вторых, смещение перигелия Меркурия больше зависит от влияния Земли и Венеры, чем от Юпитера и Сатурна, а, в-третьих, реальное абсолютное значение смещения афелия Венеры явно выбивается из этой общей зависимости. К тому же, совершенно не понятно откуда у Ньютона взялась эта зависимость, т.к. он сам же доказал, что смещения афелиев орбит одиноких планет будут только в том случае, если закон тяготения немного отличается от строго квадратичной зависимости, а у него в законе тяготения строго квадратичная зависимость и, следовательно, тут действительно «Афелии и узлы орбит неподвижны», а вот из-за чего они у него движутся от воздействия Юпитера и Сатурна я не нашел. Но, даже сама постановка вопроса о рассмотрении возмущающего воздействия других планет на орбиту конкретной планеты и попытка его решить, это в любом случае огромное достижение Ньютона.

Таким образом, «Математические начала натуральной философии» Ньютона это действительно только самое начало описания законов Природы и только попытка перевести их на язык математики и поэтому и сами законы можно трактовать не однозначно и многие выводы, сделанные Ньютоном, являются ошибочными. Так, например, из неоднозначной формулировки Ньютоном 2-го закона вытекает и неоднозначная интерпретация его 3-го закона. Ведь современная интерпретация о том, что сила действия равна силе противодействия, т.е. F1=F2, в корне противоречит тому, что написал Ньютон и соответствует только формулировке Леонардо да Винчи, когда он рассматривает силы, действующие от весла лодки на воду и воды на лодку. Но Ньютон точно не знал об этой формулировке Леонардо да Винчи, т.к. его работы стали доступны научной общественности только после 1979 года. А в формулировке Ньютона говориться не о силах, а именно о действие и это становится окончательно ясно из его закона сохранения количества движения (см. выше следствие III), где Ньютон также поясняет «Так как по закону III действие и противодействие между собою равны, то по закону II они производят равные изменения количества движения, направленные в противоположные стороны» и рассматривает пример с ударом двух шаров, где в качестве действия явно рассматривает импульс, т.е. произведение массы на скорость, а не силы, т.е. произведения массы на ускорение. Да и в самих законах, т.е. в 1-м и 2-м он ясно использует термин силы, а в 3-м пишет именно о действии. Можно, конечно, попытаться понять о чем пишет Ньютон и из его словесных пояснений, например, поясняя свой 3-й закон он пишет.

Если что-либо давит на что-нибудь другое или тянет его, то оно само этим последним давится или тянется. Если кто нажимает пальцем на камень, то и палец его также нажимается камнем. Если лошадь тащит, камень, привязанный к канату, то и, обратно (если можно так выразиться), она с равным усилием оттягивается к камню, ибо натянутый канат своею упругостью производит одинаковое усилие на лошадь в сторону камня и на камень в сторону лошади, и насколько этот канат препятствует движению лошади вперед, настолько же он побуждает движение вперед камня. Если какое-нибудь тело, ударившись в другое тело, изменяет своею силою его количество движения на сколько-нибудь, то оно претерпит от силы второго тела в своем собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга постоянно равны. От таких взаимодействий всегда происходят равные изменения не скоростей, а количеств движения, предполагая, конечно, что тела никаким другим усилиям не подвергаются. Изменения скоростей, происходящие также в противоположные стороны, будут обратно пропорциональны массам тел, ибо количества движения получают равные изменения. Этот закон имеет место и для притяжений, как это будет доказано в поучении.

Да, прочитав это пояснение и исходя из наших современных понятий, можно сделать вывод о том, что у Ньютона "действие" это и есть "сила", но и "силы" и "давления" и "тяги", о которых Ньютон здесь говорит, имели тогда совсем другой смысл, так же, как и его термин "мощность", о чем я писал выше. Ведь согласно учению Лейбница в то время величину m*V^2 называли “живой силой”, а термином “мертвые силы” называли "давления" или "тяги" покоящихся тел, которые измеряются произведением массы на скорость, с которой двигалось бы тело, если бы из состояния покоя оно перешло в состояние движения или наоборот, остановилось, как в случае абсолютно неупругого удара. Таким образом, "давления" или "тяги", т.е. "мертвые силы" это в то время было "количество движения" в нашем современном понимании, а не "сила", как многие подумали. И только в ХVIII века Даламбер стал утверждать, что под "силой" движущихся тел нужно понимать только их способность преодолевать препятствия или сопротивляться им, и поэтому "сила" не должна измеряться ни через m*V, ни через m*V^2. А термин "действие" стал определенным только в середине ХVIII века и в формулировке Эйлера стал означать интеграл от m*V по пути. Но даже, если предположить, что у Ньютона "сила" и "действие" это одно и то же в нашем современном понимании, то почему тогда, например, в 3-м законе у него не написано, что сила действия равна силе противодействия, а написано, что действию всегда есть равное и противоположное противодействие. Или почему он в определение V не пишет, что центростремительная сила есть действие, с которым тела и т.д., а пишет, что эта сила есть сила. И где у него определение для самой силы, а не отличия одних сил от других, которые он дает в своих определениях.

И вот именно эта неоднозначная интерпретация законов Ньютона, а также принятие им в качестве меры движения «количества движения», а не «живой силы», а также открытие позже закона сохранения энергии и побудили различных ученых создавать новые подходы для описания явлений Природы, которые имеют мало общего с импульсным подходом Ньютона. Так у Эйлера получился силовой подход, у Лагранжа, который силы Эйлера умножил на виртуальные перемещения, получился энергетический подход, т.к. сила, умноженная на перемещение, это работа (хотя Лагранж об этом и не знал, а к тому же сделал это ошибочно). Я же увидел в принципе Даламбера уравнение мощностей и получил мощностной подход, а у Герца получился чисто кинематический (геометрический) подход, т.к. он в основу своего подхода положил дифференциальный вариационный принцип Гаусса. При этом Ньютонов подход с его количеством движения как-то не прижился в науке и не был в дальнейшем четко изложен в аналитической форме. Правда, в квантовой механике, где количество движения вроде бы играет (иногда, когда это нужно) какую-то роль этот подход частично используется.

А теперь давайте я изложу свой взгляд на подход Лагранжа, где он получил основное уравнение (общую формулу) динамики, о котором все забыли, и применил особый математический прием, который все принимают за его основное уравнение динамики. При этом я буду постоянно сравнивать механику Лагранжа и механику Эйлера, а также покажу, как они оба могли прийти, к моему мощностному подходу. Собственно говоря, саму динамику Лагранжа можно изложить на трех страничках, что я сейчас и сделаю, но сначала я дам маленький кусочек из его статики, который нам пригодиться для выяснения, что же Лагранж называет силой, а что моментом силы.

«1. Общий закон равновесия машин заключается в том, что силы относятся друг к другу обратно отношению скоростей точек, к которым они приложены, причем скорости должны измеряться по направлению этих сил.

В этом законе заключено положение, которое обычно называют принципом виртуальных скоростей. … Таким образом дифференциалы dp, dq, dr, … будут пропорциональны виртуальным скоростям сил P, Q, R, … и, следовательно, могут быть для простоты подставлены вместо этих скоростей»

«2. Итак, вообще для равновесия любого числа сил P, Q, R, …, направленных по линиям p, q, r, …  и приложенных к любой системе тел или точек, расположенных любым образом, мы имеем уравнение следующего вида:

P*dp + Q*dq + R*dr + … =0

Это – общая формула статики для равновесия любой системы сил.

Мы назовем каждый член этой формулы, например P*dp, моментом силы P, и примем слово момент в том смысле, который ему придал Галилей, т.е. как произведение силы на ее виртуальную скорость;  тогда приведенная выше формула статики гласит: сумма моментов всех сил равна нулю».

Ну, что тут можно сказать. Вполне все резонно. Кроме одного. Надо бы знать элементарные вещи в механике, т.к. у Галилея моментом (импульсом) было произведение массы на скорость, а не силы на скорость, да и замена Лагранжем виртуальных скоростей виртуальными перемещениями равносильна замене мощности на работу, а это тоже принципиальная ошибка. Ну и теперь самое интересное – динамика. А здесь мы видим, что Лагранж представляет ее также туманно, как и все те, кто спорил о двух мерах механической формы движения материи, и о которых я писал в работе [7]. Вообще то, это частично можно объяснить тем, что, когда Лагранж писал свою Аналитическую механику еще не существовало таких понятий как энергия и мощность, хотя уже был закон сохранения живых сил и о том, что такое сила Эйлер дал очень внятные объяснения. Но, тогда непонятно зачем Лагранжу было «выпендриваться» и показывать свои якобы познания в механике и «приплетать» сюда вариационное исчисление, которое они с Эйлером создали для решения геометрических задач на максимум и минимум. Ведь Эйлер давным-давно дал аналитическое описание механики и, в конце-то концов, описал все правильно и я пользуюсь практически его формулами. А у Лагранжа мы читаем вот это.

«1. Когда силы, действующие на систему тел, распределены соответственно законам, изложенным в первой части настоящего сочинения, то эти силы взаимно уничтожаются и система остается в равновесии. Но если равновесия не существует, то тела необходимо должны двигаться, следуя полностью или частично влиянию действующих на них сил. Определение движений, вызываемых заданными силами, и составляет предмет настоящей второй части «Аналитической механики».

       Мы будем рассматривать главным образом силы ускоряющие и замедляющие, действие которых, подобно действию силы тяжести, непрерывно и которые стремятся каждое мгновение сообщить бесконечно малую и одинаковую для всех частиц материи скорость.

       В том случае, когда эти силы действуют свободно и равномерно, они необходимо вызывают скорости, которые возрастают пропорционально времени; сообщенные таким образом за заданное время скорости можно рассматривать, как наиболее простое действие этого рода сил, которое, следовательно, является наиболее подходящим для измерения. Простые действия этих сил в механике следует признать известными и все искусство этой науки заключается только в том, чтобы из них вывести сложные эффекты, которые должны получиться в результате соединенного и модифицированного действия этих сил.

2, Итак, допустим, что для каждой ускоряющей силы известна скорость, какую она способна сообщить в течение определенного промежутка времени, который мы примем в качестве единицы времени, движущемуся телу, действуя на него все время одинаковым образом, и будем измерять ускоряющую силу именно при помощи этой самой скорости; последняя же в свою очередь должна измеряться тем пространством, которое движущееся тело прошло бы в течение такого же времени, если бы оно продолжало двигаться равномерно; на основании теорем Галилея известно, это последнее пространство всегда вдвое больше пространства, фактически проходимого телом под постоянным действием ускоряющей силы.

        Вообще какую-нибудь ускоряющую силу можно принять в качестве единицы и к ней относить все прочие силы. Тогда в качестве единицы пространства следует принять удвоенную величину того пространства, которое под влиянием той же равномерно движущей силы тело пройдет в течение промежутка времени, принятого в качестве единицы времени, а скорость, полученная за то же время под постоянным действием той же силы, будет в этом случае единицей скоростей.

       Так, например, если в качестве единицы ускоряющих сил принять силу тяжести на широте Парижа и время измерить в секундах, то тогда следует 30,196 парижских фута принять в качестве единицы пройденных пространств, т.к. 15,098 – это высота, с которой на этой широте падает в одну секунду тело, предоставленное самому себе; в этом случае единицей скоростей будет та скорость, которую падающее тело приобретает, пройдя указанную высоту.

3. Установив эти предварительные определения, рассмотрим систему тел, расположенных совершенно произвольным образом и находящихся под действием каких угодно ускоряющих сил.

Пусть m – масса любого из этих тел, которое мы будем рассматривать в качестве точки; для простоты отнесем абсолютное положение этого тела к концу любого промежутка времени t к трем прямоугольным координатам x, y, z. Эти координаты мы будем предполагать всегда параллельными трем осям, неподвижным в пространстве, называемом началом координат; тогда, следовательно, эти координаты выразят прямолинейные расстояния тел от трех плоскостей, проходящих через эти же оси.

       В силу взаимной перпендикулярности указанных плоскостей координаты x, y, z выражают те расстояния, на которые тело при своем движении отдалилось от этих плоскостей, следовательно,

dx/dt, dy/dt, dz/dt выразят те скорости, которые рассматриваемое тело имеет в некоторое мгновение, чтобы удалиться от каждой из этих плоскостей и двигаться в сторону возрастающих координат; если бы тело затем было представлено самому себе, то согласно основным принципам теории движения эти скорости остались бы в последующие мгновения постоянными.

       Однако, вследствие существования между телами связи и под действием влияющих на них ускоряющих сил, эти скорости в течение мгновения dt получат приращения d(dx/dt), d(dt/dt)/ d(dz/dt), которые надлежит определить. Эти приращения можно рассматривать, как новые скорости, сообщенные каждому телу, и если их разделить на dt, мы будем иметь меру ускоряющих сил, необходимых для того, чтобы вызвать эти приращения; в самом деле, как бы ни было изменчиво действие какой-либо силы согласно природе дифференциального исчисления мы можем ее всегда принять постоянной в течение бесконечно малого времени; тогда скорость, сообщенная этой силой, пропорциональна произведению силы на время; следовательно, сама сила будет выражена с помощью отношения скорости ко времени.

         Если элемент времени dt принять в качестве постоянной величины, то рассматриваемые ускоряющие силы выразятся через d2x/dt2, d2y/dt2, d2z/dt2, а если эти силы помножить на массу m тела, на которое они действуют, то m*d2x/dt2, m*d2y/dt2, m*d2z/dt2 выразят силы, примененные непосредственно для того, чтобы в течение времени dt двигать тело m параллельно осям x, y, z. Таким образом каждое тело m системы можно рассматривать как находящееся под действием подобных сил; следовательно, все эти силы должны быть эквивалентны тем силам, под влиянием которых согласно допущению находится система и действие которых видоизменяется вследствие природы самой системы; поэтому согласно теореме, приведенной в первой части (отд. 11, п. 15), сумма моментов первых всегда должна быть равна сумме моментов вторых.      

6. Ясно, что эта формула отличается от общей формулы статики, приведенной в первой части (отд. II), только членами, обязанными своим происхождением силам m*d2x/dt2, m*d2y/dt2, m*d2z/dt2, вызывающим ускорения тела по направлению возрастающих координат x, y, z. В самом деле, в предыдущем отделе (п. 11) мы видели, что эти силы, взятые в противоположном направлении, т.е. таким образом, как если бы они стремились укоротить линии x, y, z, должны уравновесить действующие силы P, Q, R, …, которые согласно предположению должны стремиться укоротить линии p, q, r, … . Таким образом следует только к моментам последних сил прибавить моменты сил m*d2x/dt2, m*d2y/dt2, m*d2z/dt2 для каждого из тел m, чтобы от условия равновесия тотчас же перейти к свойствам движения (ч. I, отд. II. П. 4).»

Теперь разбор полетов. Я уже написал о том, что Лагранж не знал чему равен момент у Галилея, а поэтому он свои силы в правой части его общей формулы непонятно зачем умножил на массы, что является ошибкой. Ведь, если мы посмотрим на его те же самые силы в статике, то там они даны без масс, а он в 6-м пункте пишет, что эта формула отличается от основной формулы в статике только наличием левой части. Вот эта ошибка Лагранжа и привела к тому, что у Гербера в его манипуляциях (6) получилось, что ускорение равно силе и даже по размерности получившихся величин Гербер должен был ее заметить, но быстрее всего, как все математико-физики он о таких мелочах не задумывался, а слепо веровал в гений Лагранжа, но на этом моменте я остановлюсь подробно позже. А сейчас остановимся но том, что Лагранж путается и с определением сил инерции, т.к. он в конце 3-го пункта пишет «рассматриваемые ускоряющие силы выразятся через d2x/dt2, d2y/dt2, d2z/dt2, а если эти силы помножить на массу m тела, на которое они действуют, то m*d2x/dt2, m*d2y/dt2, m*d2z/dt2 выразят силы, примененные непосредственно для того, чтобы в течение времени dt двигать тело m параллельно осям x, y, z.» Но, ускоряющими силами Эйлер, у которого Лагранж и передирал все связанное с аналитикой в механике, называл ускорения в первых томах механики, а в третьем томе у него ускорения уже используются как привычные нам ускорения, но Лагранж в этом просто не разобрался.

Здесь надо сделать некоторое пояснение. До Эйлера не существовало даже формул для вычисления скорости и ускорения и для того, чтобы написать, что V=s/t для равномерного движения и V=ds/dt для мгновенных скоростей надо было подняться на новый уровень абстракций и Эйлер это сделал, т.к. был не только величайшим математиком (геометром) всех времен и народов, но еще и философом. А вот в первых томах он действительно именует ускорения ускоряющими силами, но при этом он рассматривает движение тел в поле тяжести Земли и использует понятие «высоты скорости», т.е.  высоты соответствующей этой скорости при падении тела с этой высоты. Поэтому, там у Эйлера это все выглядит логично и у него действительно получается, что при падении тела путь который оно проходит за время t оказывается в два раза меньше пути, равного скорости в конце падения умноженной на это время t.

Вот и у Лагранжа мы во 2-м пункте тоже видим пространные рассуждения о том, что используемые расстояния, должны быть в два раза больше реальных расстояний, и он приводит расчет для падения тел в Париже. Но он совершенно не понял, что у Эйлера это расстояние используется для решения практических задач в рассмотренной им системе единиц измерения и только для равноускоренного движения, где у него получился коэффициент пропорциональности 250 для рейнского фута, что пишет Эйлер легко запомнить. Лагранж же нам приводит основное уравнение для произвольного движения, к которому эти расчеты совершенно не относятся. Поэтому, я думаю, никто из читающих, приведенный мною выше текст его именно механики, и не понял, т.к. совершенно непонятно зачем здесь это удвоение расстояний во 2-м пункте. А у Эйлера для произвольного движения тела по трем координатным осям в 3-м томе получились вот такие уравнения (я заменю обозначения для силы и массы на современные, а в тексте у него «тельце» это маленькая масса, т.е. точка, но не бестелесная).

d2x/dt2 = n*Fx/m                                                                          (1)

d2y/dt2 = n*Fy/m    

d2z/dt2 = n*Fz/m     

где d2x/dt2, d2y/dt2, d2z/dt2 – вторые производные по времени от перемещений тела по осям x, y, z, т.е. ускорения, Fx, Fy, Fz – силы стремящиеся изменить состояние тела по этим осям, а n – коэффициент пропорциональности для согласования различных единиц измерения пути, времени, скорости, силы и массы. И Эйлер пишет [19] «Тремя уравнениями подобного вида может быть представлено изменение всяких движений, как бы ни действовали силы на тельце, а так как эти уравнения вполне сходны между собой, то можно даже считать, что вся механика основывается на одном единственном принципе». А основа всей механики в первых томах у Эйлера заключается в следующем едином законе, который Эйлер формулирует так

«Если на тельце, масса которого равна m, действует сила, равная F, и если после разложения движения по направлению силы тельце за промежуток времени dt проходит отрезочек пути ds со скоростью ds/dt=V, то d2s/dt2 = n*F/m  или dV=n*F*dt/m.

Таким образом, приращение скорости, взятое по направлению действующей силы, прямо пропорционально времени и обратно пропорционально массе тельца».

Как видим, в Аналитической механике Эйлера полный порядок, а вот от Аналитической механики Лагранжа остался один пшик, если не считать его чисто математических методов исключения переменных в дифференциальных уравнениях и его упрощенного (чисто математического) метода получения дифференциальных уравнений, который автоматически позволяет до минимума сократить число переменных в дифференциальных уравнениях. Т.е. речь идет о его формуле (2), которую он получил, сочетая его ПНД и принципы вариационного исчисления. Сам Лагранж об этом методе, сравнивая его со своей общей формулой (основным уравнением) динамики, писал

«1. Достаточно развернуть ту формулу, к которой мы свели во втором отделе всю теорию динамики, чтобы получить все уравнения, необходимые для решения любой задачи в данной отрасли знания, в чем бы она не заключалась; но это применение формулы, представляющее собою чисто вычислительную операцию, может быть в некоторых отношениях еще упрощено с помощью тех приемов, которые мы применим в настоящем отделе.

Так как все дело сводится к тому, чтобы свести различные переменные, входящие в состав указанной формулы, к возможно меньшему числу, пользуясь условными уравнениями, заданными природой каждой задачи, то одна из главнейших операций заключается в том, чтобы вместо заданных переменных подставить функции других переменных. Эта цель может быть всегда легко достигнута с помощью обычных методов; но по отношению к рассматриваемой формуле существует особый прием выполнения этой операции, имеющий то преимущество, что он всегда непосредственно приводит к более простым преобразованиям.

2. Упомянутая формула состоит из двух частей, которые должны быть рассмотрены отдельно. Первая часть... Сумма этих двух величин, будучи равна нулю, и дает общую формулу динамики (отд.II п.5).»

Таким образом, его общая формула динамики дает те же дифференциальные уравнения, где потом надо уменьшать число переменных, а его формула (2) позволяет получить сразу минимальное число уравнений и переменных. Здесь у него T- кинетическая энергия, V- силовая функция, R- обобщенная координата, а Vr- скорость по этой обобщенной координате. Но Гамильтон додумался до того, что у него потенциальная энергия может зависеть и от времени, а поэтому уравнение (2) ему не подходит. И он вводит в обращение свой лагранжиан L=T-U (T- кинетическая энергия, а U- потенциальная) и формулирует свой ПНД, где функционалом является не кинетическая энергия, как у Лагранжа, а его (Гамильтона) лагранжиан. И теперь для получения дифференциальных уравнений, описывающих поведение системы, надо проводить колдовские манипуляции уже с его лагранжианом согласно выражению (3), которое в развернутом виде будет выглядеть как (4). Но, если не рассматривать его частный случай, когда  потенциальная энергия может зависеть от скорости или от времени, то и его ПНД даст те же уравнения, что и ПНД Лагранжа по формуле (2), если вместо силовой функции V у Лагранжа записать потенциальную энергию U Гамильтона.

d(dT/dVr)/dt – dT/dR + dV/dR =0                                       (2)

d(dL/dVr)/dt - dL/dR =0                                                       (3)

d(dT/dVr)/dt - d(dU/dVr)/dt – dT/dR + dU/dR =0               (4)

Ведь какой бы ПНД мы не использовали для поиска экстремалей, согласно формулам Эйлера для решения геометрических задач, мы должны, в конце-то концов, получить одни и те же дифференциальные уравнения для одной и той же системы. Но в формуле (2) у Лагранжа V это не обязательно потенциальная энергия U, а просто силовая функция, которая может включать в себя и силы трения, с которыми мучился Ландау, изобретаю какую то диссипативную функцию, чтобы применить этот метод в формулировке Гамильтона. А у Гамильтона уже используется T-U и поэтому силу трения нельзя вводить в выражение для потенциальной энергии (вообще-то, ее никуда нельзя вводить, если использовать ПНД, т.к. он при этом явно не работает). А у Лагранжа эта сила трения просто добавляется к силовой функции и в начале 2-го тома он пишет «Если бы движение происходило в сопротивляющейся среде, то, обозначив сопротивление через R, следовало бы лишь к значению dV прибавить члены (отд. II, п. 8) … , но в этом случае уравнение T+V=H уже не имело бы места». Таким образом, в колдовских манипуляциях в уравнении (2) Лагранж не видит ничего божественного, т.к. уравнение это работает и в этом случае, а ПНД уже не работает, т.к. не выполняется закон сохранения живых сил.

Следовательно, к самому ПНД эти манипуляции уже никакого отношения не имеют и являются формальными манипуляциями, чтобы из T и V получить выражение для силы инерции и силы создаваемой потенциальным полем, в котором находится это тело. Просто здесь у Лагранжа для расчета T и V используются не все Декартовы координаты, а только обобщенные координаты, число которых сведено к минимуму, и поэтому и получается минимальное количество дифференциальных уравнений. А, если не ставить себе задачу во что бы то ни стало облегчить жизнь математиков, т.е. уменьшить число дифференциальных уравнений, описывающих реальную систему с использованием силового подхода Эйлера, который позволяет получить корректное дифференциальное описание системы, то все эти колдовские манипуляции Лагранжа и Гамильтона совершенно не нужны. Но в науке возобладал подход, который поддерживается и сегодняшней Академией наук, о том, что это Бог управляет каждым атомом во вселенной и ПНД является отражением этих разумных действий Бога. Поэтому, выполняя колдовские манипуляции с лагранжианом, ученые и не задумываются о том, почему и зачем надо делать именно так. Ведь ответ известен – так угодно Богу. А Гамильтон, у которого потенциальная энергия может зависеть и от времени, дал формальный повод не задумываться почему она может зависеть и от скорости, т.к. всегда можно записать, что dt=dR/dVr. Вот Вебер с Гербером и нафантазировали, что потенциальная энергия может зависеть и от скорости, даже не задумавшись о природе потенциальной энергии. Например, у Гербера его потенциал (в то время это означало потенциальную энергию) выражался формулой (5), где Vr это скорость массы m относительно массы M, R - расстояние между ними, а c - это скорость гравитации.

P = G*M*m / [R*(1 – Vr/c)^2]                                            (5)

(dT/dR)/m – d(dT/dVr)/dt /m = dP/dR – d(dP/dVr)/dt        (6)

Но получение так называемых запаздывающих потенциалов Вебера или Гербера это только пол дела, т.к. для описания поведения систем нам нужны ускорения масс системы, а их мы определяем через силы, действующие на тело с массой m. И тут мы видим во всей красе нелепости, вытекающие из формального энергетического подхода Лагранжа в механике. Ведь Гербер, не моргнув глазом, имея ввиду свое выражение (5), где у него в тексте P обозначено как V, пишет, что «Здесь в этом выражении для V содержатся не только R  но и производная от R по времени. Поэтому благодаря общим уравнениям движения по Лагранжу для ускорения массы m получаем» и применяет колдовские манипуляции Лагранжа для своего потенциала точно так же, как и для кинетической энергии (6). Здесь сразу бросается в глаза нелепость того, что Гербер ускорение в левой части приравнял силе в правой части, но тут он, можно сказать, не виноват, т.к. это у Лагранжа в Аналитической механике получается путаница с массами, когда он выводит свою основную формулу динамики, что мы видели выше. А, если выполнить манипуляции предложенные Гербером, то в правой части действительно получается выражение для силы, которое и получил Гербер.

При этом, проделав указанные манипуляции с кинетической энергией T= m*Vr^2/2, мы получим минус d2R/dt2, т.е. и ускорение и сила притяжения у нас получились со знаком минус или можно сказать, что обе величины будут с плюсом. Таким образом, уравнение, полученное с использованием выражения (6) будет отражать у Гербера не закон тяготения, а закон отталкивания. Более того, манипуляции Гербера (6) соответствуют и манипуляциям Гамильтона (4), если все знаки заменить на противоположные, а значит и у ускорения тоже получится отрицательный знак, т.е. мы опять таки получим закон отталкивания, а не притяжения. Странно только, что даже эту элементарную ошибку никто у Гербера не заметил, т.е. мы видим, что оболванивание ученых уравнениями Лагранжа уже в то время было на очень высоком уровне. К тому же я ума не приложу какое отношение к кинетической энергии тела m в формуле (6) имеет скорость тела M относительно него, т.к. Vr это у него относительная скорость двух тел.

При этом обращаю Ваше внимание, что найти хоть какую ни будь ошибку у Гербера при выводе им формулы для расчета аномального смещения перигелия Меркурия в течение двадцатого века пытались очень многие математико-физики, но так и не смогли. А связано это было с тем, что Гербер в этой своей работе [22] получил формулу для расчета аномального смещения перигелия Меркурия, которая в точности повторяла формулу Эйнштейна, но получил он ее без всякой ОТО, т.к. получил ее еще в 1898 году, а в 1902 дал более подробный вывод. Но, как видим, они не смогли обнаружить даже элементарных ошибок с размерностью и со знаками, о которых я только что написал, а в своей работе [14] я привожу еще несколько ошибок Гербера при выводе этой формулы. И там же я пишу о том, что эти математико-физики проделали просто какой то фокус-покус с потенциалами Вебера, чтобы хоть как то их притянуть к манипуляциям Лагранжа. Таким образом, квалификация математико-физиков двадцатого века, мягко говоря, оставляла желать лучшего, но, забыв об Эйлере и связавшись с Лагранжем, ничего другого они сделать и не могли.   

И, в конце-то концов, эти грамотеи двадцатого века смогли создать с использованием энергетическо-геометрического подхода Лагранжа и Гамильтона, т.е. подхода опирающегося на ПНД, теорию относительности и квантовую механику. Но, если у Лагранжа мы еще видим какие то следы от механики, т.к. основным методом получения дифференциальных уравнений он все таки считал не манипуляции (2), а свою основную формулу динамики, то у Гамильтона мы не видим и этих следов, и вся механика и оптика у него заключены в формуле (3). И, наконец, этот Лагранжево-Гамильтонов формализм привел к тому, что ученые совершенно перестали выводить уравнения, описывающие явления Природы, а стали их просто отгадывать, полностью положившись в этом вопросе на Бога, т.е. на ПНД. И вот до какой чертовщины они при этом дошли, например, в квантовой механике [25], где ПНД Гамильтона Девитт называет принципом стационарного действия (ПСД). Конкретно он пишет

«Теперь мы готовы к тому, чтобы исследовать проблему измерения. Связь системы с прибором, которая с математической точки зрения наиболее удобна для анализа измерения одной наблюдаемой A, описывается (по крайней мере приближенно) полным функционалом действия вида

Ss + Sp + g*x*A.           (4.15)

Здесь Ss – функция действия системы, Sp – функция действия прибора, x – некоторая удобная переменная, описывающая прибор, g – «константа связи». Можно указать два примера, когда связь этого общего типа имеет место в реальных измерениях.

   1) Опыт Штерна-Герлаха. В данном случае А – это проекция спина атома на единичный вектор в направлении магнитного поля. «Системой» является только спин, в то время как «прибор» состоит из (а) самого атома, (б) магнитного поля и (в) лабораторной системы координат. Если атом достаточно массивен, то в низшем приближении можно пренебречь динамикой спина и считать, что Ss=0 (или Ss=const). Действие же прибора можно взять в виде

Sp = ∫ 0,5*m*((dx2/dt)^2 + (dx3/dt)^2)*dt,

где m – масса атома, а x2 и x3 его координаты

 ...............

2) Измерение электрического поля *). В этом случае в качестве прибора удобно выбрать равномерно заряженное пробное тело, имеющее форму куба

.....................

Бор и Розенфельд показали, что в действительности этот результат можно улучшить. Для этого нужно изменить полное действие (4.15) следующим образом:

Ss + Sp + g*x*A – g^2*x^2*Da*A.           (4.34)

Кроме члена взаимодействия здесь присутствует еще член второго порядка (-g^2*x^2*Da*A), называемый компенсационным членом. ..........»

Так вот я не понимаю причем здесь прибор и члены (взаимодействия и компенсационный) по крайней мере в опытах Штерна-Герлаха. Ведь здесь для вывода дифференциальных уравнений вполне применим подход Эйлера, а при выводе из лагранжиана классический ПНД Гамильтона с требованием только стационарности действия. Ведь мы имеем две классические точки траектории 1- испаритель серебра и 2 – прибор (стеклянная пластина) между которыми атомы серебра движутся свободно, а в середине пути определенное время в магнитном поле. Так зачем же изобретать весь этот огород с прибором и дополнительными членами.  И какое тут может быть действие у прибора, т.е. стеклянной пластины и какое может быть действие взаимодействия атома с этой пластиной. Ведь нам надо найти траекторию, по которой пролетели атомы серебра между точками 1 и 2, а какой там стороной и как крепко они прицепились к стеклянной пластине в точке, где они встретились с пластиной, нас совершенно не интересует.

И что это еще за фокус, когда действие системы у Девитта равно только спину атома. И причем тут вообще спин, который является просто параметром атома таким же как, например, его масса. Или может быть рационализатор Девитт считает, что у него спин имеет размерность действия и поэтому его тоже можно считать действием в ПНД. И с какого перепугу действие прибора, фиксирующего изменение каких то параметров системы, определяется массой и скоростью движения тела, конечную точку траектории которого мы и фиксируем этим прибором. А уж про члены взаимодействия и компенсационный я вообще молчу. Таким образом, то, что изобрели рационализаторы Бор и Розенфельд и то, что представил Девитт в своей книге не имеет никакого отношения даже к ПНД, т.е. после их рацпредложений их ПСД это уже просто ничего не значащий принцип с которым можно обращаться совершенно произвольно не соблюдая никаких принципов.

Вот только я считаю, что Девитту и компании, если им так уж хочется заняться рационализаторством, то и не надо было бы сюда «приплетать» ПНД, чтобы придать процессу рационализаторства якобы научную основу, а сразу бы занялись рацпредложениями по видоизменению лагранжиана. Ведь в конечном итоге, им для получения уравнений движения надо дифференцировать лагранжиан с набором манипуляций (3). Вот Планк [9], когда подгонял формулу своего статистического распределения под законы излучения абсолютно черного тела, так и написал «… я в конце концов приступил к построению произвольных уравнений для энтропии …. Особенно привлекательно одно из построенных мною выражений…». Иначе говоря, он записывал произвольные выражения для энтропии, а потом смотрел, что из этого получится. И в этом процессе отгадывания здравому смыслу уже просто нет места, т.к. здесь не может быть никакой логики  кроме логики двоечника, которому все равно, что на что делить и умножать, а главное, чтобы результат совпал с ответом в конце задачника.

Но, как видим, именно этот метод познания Природы (с использованием ПНД Гамильтона) и прославляет официальная наука, а заодно и поет дифирамбы Лагранжу, как великому механику. А вот про Эйлера, что-то, ничего не слышно и его работы, по крайней мере, на русском языке найти не возможно, кроме его усеченной механики (в 1938 году была опубликована книга «Основы динамики точки» [19], где приведены только первые главы из его собственно механики и из теории движения твердых тел), и работы по теории Луны. Да и те найти можно с трудом, хотя большая часть работ Эйлера была опубликована в Петербурге (правда на латыни). Быстрее всего, это связано с тем, что они на фундаментальном уровне обосновывают силовой подход описания явлений Природы, а не энергетическо-геометрический, взятый на вооружение квантовой и релятивистской механиками. А ведь у Эйлера не только основательно рассматриваются такие понятия как пространство, время, масса и сила, но и дается простой и понятный метод описания явлений Природы. Вот только, при этом, он в основном говорит об абсолютном пространстве и упоминает еще о некоторой тонкой материи исчезающей от наших чувств, при рассмотрении вопроса действия сил на расстоянии, т.е. намекает на эфир. И хотя Эйлер так и не дает окончательного заключения о наличии только абсолютного движения, т.к. нам это не дано в наших ощущениях, и мы можем наблюдать только относительные движения, но я думаю этих его высказываний достаточно, чтобы Академии наук причислить Эйлера по современной терминологии к альтернативщикам и молчать о его Аналитической механике.

Интересно отметить и то, что у Эйлера есть и несколько другая запись своего принципа в первых томах V*dV = n*F*ds / m. Перенесем m из знаменателя правой части в левую часть и разделим обе части на dt. Получим m*V*dV/dt = n*F*ds/dt или V*m*d2s/dt2 = n*V *F. Здесь n это у него коэффициент пропорциональности и, если все рассматривать в системе СИ то он будет равен единице, и мы получим уравнение мощностей, о котором я говорю в своем 4-м подходе описания законов Природы. И это становиться отчетливо видно, если принять, что выражение m*d2s/dt2 это будут силы инерции Fj. Да, даже, если выкинуть у Лагранжа из его основной формулы нелепое m в правой части и принять виртуальные скорости именно виртуальными скоростями, а не виртуальными перемещениями, как это ошибочно сделал Лагранж, то опять-таки получится мое уравнение мощностей. И мы видим, что и Эйлер и Лагранж ходили вокруг да около моего уравнения мощностей, но в то время не было таких понятий как энергия и мощность, поэтому они уходили от него – один к уравнению сил, а другой к уравнению энергий, хотя при этом Лагранж и понятия не имел об энергии.

А суть моего мощностного подхода заключается в том, что изменение кинетической энергии тела за элемент времени dt равно сумме мощностей от всех внешних сил, действующих на это тело и, если эта мощность увеличивает координату, то она берется со знаком плюс, а если уменьшает, то со знаком минус, а мощность пошедшая на диссипацию энергии всегда берется со знаком противоположным знаку скорости движения тела. Таким образом, мой мощностной подход к описанию явлений Природы ни сколько не противоречит силовому подходу Эйлера и поэтому все определения для пространства, времени, массы и силы, данные Эйлером можно использовать и при моем подходе. А мне остается только дать определения мощности и энергии, а также немного расширить понятие силы потому, что Эйлер разделял силы на внешние и силы инерции.

Причем, о последних он в первых томах даже старался не говорить как о силах. И в его формулировке определение силы звучит так «Все, что способно изменять абсолютное состояние тела, называется силой». А далее он уточняет «Так как под влиянием внутренних причин тело должно было бы сохранять свое состояние, силу следует считать внешней причиной». У Эйлера "силы инерции" сохраняют состояние тела и поэтому не подпадают под эту формулировку, но я считаю, что для обеих сил можно дать одну общую формулировку. «Сила это то, что нам дано в наших ощущениях, как видимый (чувственный) результат взаимодействия между телами в пространстве. При этом силы или стараются изменить абсолютное состояние тела (внешние силы) или стараются сохранить абсолютное состояние тела, т.е. его покой или движение (силы инерции)». Тогда для мощности и энергии можно дать следующие определения. «Мощность это мгновенный (текущий) результат взаимодействия между телами в абсолютном пространстве и во времени, а энергия это интегральный результат этого взаимодействия в абсолютном пространстве и во времени».

Таким образом, основная идея моего мощностного подхода заключается в том, что сила Fik, с которой одно тело i будет воздействовать на другое тело k, которая нам нужна для нахождения ускорений тела k, будет определяться из зависимости Fik= Nik/Vk, где Nik это мощность подведенная от i-го тела к k-у, а Vk это скорость k-го тела. Например, если мы рассмотрим движение ракеты, в двигателях которой будет постоянно сжигаться одно и тоже количество топлива, т.е. мощность двигателей будет постоянной, и при этом кинетическая энергия газов будет полностью переходить в тягу двигателя, то согласно приведенной зависимости с ростом Vk у нас будет уменьшаться Fik и ракета должна получать все более меньшее ускорение и, следовательно, ее скорость должна расти все медленнее и медленнее. Т.е. здесь все объясняется без мифического увеличения массы тела с ростом его скорости, когда, якобы, сила тяги остается постоянной, хотя именно сила, ускоряющая обычную топливную ракету, т.е. с переменной массой, действительно будет оставаться постоянной, но это частный случай, когда дополнительная сила равна силе инерции массы сгораемого топлива. И ниже я подробно рассмотрю конкретные примеры разгона топливной и безтопливной ракеты, чтобы объяснить откуда берется эта дополнительная сила.

При этом скорость света не является никаким принципиальным пределом скорости топливной ракеты. Данное ограничение на предельную скорость возникает только при взаимодействии тел через поля, которые распространяются с конечной скоростью, как это мы наблюдаем при разгоне частиц в ускорителях.  А, т.к. на сегодняшний день в нашем арсенале воздействия на разгоняемые массы имеет наибольшую скорость передачи воздействия только электромагнитное воздействие, а оно распространяется со скоростью света то, следовательно, мы и не можем при этом воздействии разогнать массы до большей скорости. А вот скорость распространения гравитационного воздействия гораздо больше скорости света и если бы мы умели управлять этим воздействием, то мы могли бы разгонять частицы до скоростей больше скорости света. И возможно, что во вселенной можно обнаружить тела со сверхсветовой скоростью, хотя вероятность их обнаружить чрезвычайно мала, т.к. при взаимодействии двух масс они притягиваются друг к другу и чаще всего происходит их столкновение. Но теоретически возможна и такая комбинация взаимодействий нескольких тел, когда при этом столкновение не произойдет.

Интересно отметить, что к аналогичному выводу об уменьшении действующей на тело силы, а не увеличению массы тела с ростом скорости пришел и автор работы [26], который все объясняет правильной трактовкой преобразований Лоренца. И хотя мне эти преобразования Лоренца не нравятся ни в какой трактовке, т.к. я считаю такой подход слишком упрощенным и формальным, я бы все же рекомендовал ознакомиться с работой [26], где при анализе теории относительности автор получает очень интересные выводы, например, о том, что формулы Эйнштейна для расчета поступательной и поперечной сил в движущейся ИСО позволяют найти абсолютную скорость этой системы. Но все это у него становится заметно только при очень больших скоростях, а мой мощностной подход позволяет получать правильные результаты и при обычных скоростях. Например, чтобы разогнать автомобиль со скорости 110 км/час до скорости 120 км/час за одно и тоже время потребуется мощность гораздо больше, чем при разгоне его со скорости 10 км/час до скорости 20 км/час и топлива мы при этом сожжем гораздо больше. А при одинаковой мощности развиваемой двигателем у нас сила, которая будет разгонять автомобиль, при 10 км/час будет гораздо больше, чем при 110 (если при этом будет достаточное сцепление колес с опорным основанием).

В своей статье [7] я, рассматривая вопрос о двух мерах механической формы движения материи, который возник, когда не существовало таких понятий как сила, энергия и мощность, высказал утверждение, что Даламбер, сформулировав свой принцип в словесной форме и в тех терминах, которые тогда использовались, имел ввиду именно мощности, а не силы, как это трактуется в современной (Эйлеровской) интерпретации его принципа. Таким образом, мой подход отличается от силового только интерпретацией принципа Даламбера, но при этом у нас появляется возможность использовать как силовой подход, так и энергетический. Ведь мощность можно интерпретировать и как произведение силы на скорость и как энергии деленной на время. Да, при этом гипотетически могут быть какие-то замечания Герца, относящиеся к силам, но полностью отпадают его замечания касающиеся неопределенности потенциальной энергии, т.к. у нас будет только кинетическая энергия, также как и у Герца получалась только кинетическая энергия скрытых масс.

И хотя этот свой мощностной подход я впервые применил более 20 лет тому назад, но пока я его не применял к полям, поэтому не могу предложить готовых решений для этих случаев, например, для разгона частиц в ускорителях. А вот для обычных механических систем я свой принцип уже применял и получил положительные результаты. Так в своей диссертации [5] я, используя уравнение мощностей, рассмотрел движение колеса, т.е. практически качение шара с упругим проскальзыванием, о котором писал Герц, и пришел к выводу о том, что, так называемой силы сопротивления передвижению колеса, в Природе не существует. Т.е. процессы, протекающие в пятне контакта, можно описать только с использованием уравнения мощностей, также, например, как и при работе клиноременной передачи, а, исходя из силового подхода, можно только ввести фиктивную силу сопротивления качению колеса, которая где-то и как-то примерно будет отражать силовой баланс.

                                               методы математического описания систем

А теперь давайте я остановлюсь на особенностях различных подходов для описания явлений Природы при использовании различных методов описания. Начнем с того, что описание явлений Природы на языке математики может быть или интервальным или мгновенным. При интервальном описании мы описываем два положения системы на концах или интервала времени или интервала координат или интервала скоростей системы, используя законы сохранения энергии, количества движения (импульса) или момента количества движения. А при мгновенном описании мы используем дифференциальные уравнения для вторых производных от координат по времени, т.е. для ускорений элементов системы в текущий момент времени, т.е. используя принцип Даламбера или в силовом прочтении Эйлера (2-ой закон Ньютона), или в моем мощностном прочтении. При этом интервальное описании может быть и единичным (конечным), когда мы описываем систему на концах интересующих нас интервалов координат, скоростей или времени, и последовательным (текущим) когда мы разбиваем весь интервал на множество подинтервалов и используем формулы для нахождения приращений скоростей элементов системы при небольшом приращении времени или для нахождения приращения времени необходимого для заданного приращения скорости на этих подинтервалах. Далее я первое интервальное описание буду называть конечным описанием, а второе описанием в приращениях.

При этом и мгновенное описание системы, которое я буду называть дифференциальным, и описание в приращениях будут оба текущими описаниями и поэтому могут заменять друг друга, т.е. будут практически эквивалентными. И в тоже время они оба будут аналитическими описаниями в отличие от словесного описания явлений Природы в Началах Ньютона. Но при этом не надо путать аналитическое описание с аналитическим решением. При дифференциальном описании явлений Природы у нас может быть, как общее решение задачи, которое мы привыкли называть аналитическим решением, так и частное решение задачи, когда мы решаем задачу (дифференциальные уравнения, описывающие поведение системы) численными методами. А вот при описании явлений Природы в приращениях у нас изначально заложено только частное решение задачи, т.е. как бы численными методами. Но в отличие от численного решения дифференциальных уравнений, например, методом Эйлера или методом Рунге-Кутта, при численном решении задачи описанной в приращениях нам не нужны никакие дополнительные методы решения, т.к. само описание в приращениях дает нам и метод численного решения.

При этом конечное описание нам ничего не говорит о том, что происходило в системе между ее начальным положением и конечным, а текущее описание подробно описывает поведение системы на всем интервале времени между начальным и конечным положениями системы. Например, у нас есть камень, который находится на высоте h=80 м и нам надо узнать какая будет у него скорость, когда он достигнет Земли. Здесь при конечном описании мы записываем закон сохранения энергии m*V^2/2=m*g*h и отсюда находим, что V=40 м/с, т.е. получаем скорость высоты (или высоту скорости), о которой писал Эйлер. А при текущем описании мы описываем весь процесс движения камня между его начальным и конечным положениями и, например, для дифференциального описания при общем решении мы находим решение этого дифференциального уравнения для скорости и пройденного пути, а потом, решая совместно эти два уравнения, находим и нужную скорость. Вообще-то, здесь надо было бы записать закон всемирного тяготения, чтобы найти силу притяжения камня к Земле, но мы, как и при конечном описании, примем, что вблизи поверхности Земли эта сила примерно равна m*g. Тогда аналитическое решение дифференциального уравнения m*d2S/dt2=F=m*g, описывающего движение камня, будет V=g*t и S=h=g*t^2/2. Из последнего уравнения находим t=4 с и из первого V=40 м/с. При этом частное решение этого дифференциального описания, т.е. численными методами, будет подобно решению в приращениях, которое я дам чуть ниже.

Или, например, рассмотрим такую задачу. У нас есть шарик массой m привязанный к нитке, пропущенной в отверстие горизонтальной поверхности, и он движется по инерции по окружности вокруг этого отверстия с угловой скоростью w1, а длина нити равна R1. Затем нить потихоньку втягивается в отверстие до тех пор, пока шарик не начнет вращаться по окружности радиуса R2. Следует определить угловую скорость w2. Это очень типичная задача в курсе теоретической механики и решается она там на основании теоремы о сохранении момента количества движения, и, следовательно, здесь должен сохраняться так называемый кинетический момент (7), где J1 и J2 - моменты инерции (J = m*R^2).

J1 * w1 = J2 * w2 (7)

Но т.к. нас в этой задаче интересуют только начальное и конечное состояния системы, то мы можем ее решить и воспользовавшись законом сохранения энергии. Ведь, если мы посмотрим, а какова стала кинетическая энергия шарика, после того как мы его подтащили, то выясним, что она стала больше и она равна кинетической энергии при вращении по окружности R1 плюс работа, совершенная по подтаскиванию шарика из точки R1 в точку R2 . Решив это уравнение энергетического баланса, приходим к той же зависимости (7), которая и дает ответ для нашей задачи. Но, как и любую другую, эту задачу можно решить и при текущем описание этого процесса в приращениях с использованием всех подходов (импульсного, силового, мощностного и энергетического) или при текущем дифференциальном описании с использованием силового и мощностного подходов. Однако, решение этой конкретной задачи в конечном описании с использованием момента количества движения (импульсный подход) гораздо проще, чем при описании этого процесса с использованием закона сохранения энергии в энергетическом подходе (смотрите [7]) или с использованием текущего дифференциального описания в силовом подходе (смотрите мою программу Konma), поэтому, выбирая метод решения конкретной задачи, надо знать особенности того или иного описания явлений Природы.

При этом, как я писал, конечное описание является частным случаем описания явлений Природы в приращениях, т.к. здесь мы просто используем одно большое приращение между начальным и конечным положениями системы. Закон сохранения энергии для конечного описания применим всегда, а вот закон сохранения количества движения не во всех случаях потому, потому что, как я писал в работе [7], количество движения не является полноценной мерой механического движения. Этот закон не применим, когда у нас на систему действуют внешние силы не являющиеся функцией времени, а в Природе все силы являются или функцией перемещений или функцией координат и поэтому получается, что в этом случае закон сохранения  количества движения не применим никогда. Но это касается только конечного описания, а при описании явлений Природы в приращениях, когда на малом приращении времени Δt мы можем считать силу постоянной, то всегда можно с использованием закона сохранения количества движения найти и приращение ΔV. Вот, например, в нашем примере с падением камня мы можем считать силу притяжения камня к Земле постоянной на очень больших промежутках времени, т.е. можем считать, что F(t)= F=m*g=const. Поэтому мы здесь можем записать

m*(V1+ΔV)-m*V1=F*Δt                                                            (8)

Т.к. у нас начальная скорость V1 равна нулю, то у нас при первом приращении получится m*ΔV=F*Δt, где в правой части записан, так называемый, импульс силы, который в этой задаче мы можем вычислить. Теперь, если бы у нас задача была сформулирована, как найти скорость через 4 секунды, то мы бы ее нашли, решив задачу через конечное описание

ΔV=m*g*Δt/m = 10*4= 40 м/с.

А, т.к. нам надо найти скорость, когда высота станет равна нулю, то здесь мы можем найти решение этой задачи с использованием закона сохранения количества движения (импульсного подхода) только в приращениях, т.е., задавая маленькие приращения Δt и вычислять приращения скорости ΔV, а потом по средней скорости на этом отрезке времени Δt вычислять пройденный камнем путь и определять его высоту. Для примера давайте возьмем приращения Δt=1 с и решим эту задачу в приращениях.

Δt=1          t=1с        ΔV=10 м/с     V=10 м/с       Vsr=5 м/с           S=5 м           h=75 м

Δt=1          t=2с        ΔV=10 м/с     V=20 м/с       Vsr=15 м/с         S=15 м         h=60 м

Δt=1          t=3с        ΔV=10 м/с     V=30 м/с       Vsr=25 м/с         S=25 м         h=35 м

Δt=1          t=4с        ΔV=10 м/с     V=40 м/с       Vsr=35 м/с         S=35 м         h= 0 м

Здесь у нас, как частный случай, получился точный ответ и при этом шаге решения в приращениях, но обычно при решении задач с такими параметрами объектов надо использовать маленький шаг приращений Δt=0,01 с или еще меньше, чтобы получить ответ с заданной точностью. А вот при описании движения таких объектов, как планеты Солнечной системы, я в программе Solsys решаю дифференциальные уравнения методом Рунге-Кутта с шагом решения (приращением времени) равным 3600 с. Но, если мы рассмотрим задачу удара упругого шара (мяча) в абсолютно жесткую стену, которую я рассматривал в работе [7], то шаг решения надо будет брать, как минимум 0,001 с, т.к. в этом случае у нас при заданных ниже параметрах весь удар будет длиться только 0,03 с. Конкретно там я рассмотрел удар шара массой m= 1 кг и жесткостью  C= 10000 Н/м при начальной скорости V1= 10 м/с. Как при этом измененялась скорость его центра масс и сила удара, которая определится как C*X, показано на рис. 0. 

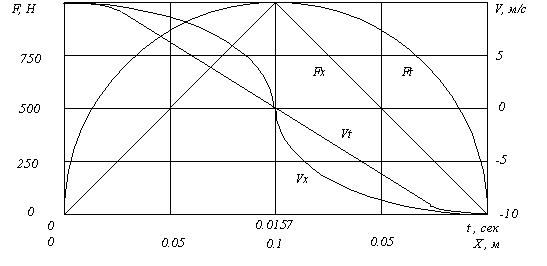
Рис. 0. Зависимости силы удара F и скорости шара V в функции его деформации X и в функции времени t. Воспроизведено из работы [7].

При решении этой задачи в работе [7] я использовал для дифференциального описания силовой подход, как частный случай мощностного подхода, но для конечного решения этой задачи удара шара в стену мы вполне можем применить и энергетический подход и можем или по заданной деформации шара найти конечную скорость или по конечной скорости найти получающуюся деформацию. Например, нам надо найти его скорость при деформации X=0,05 м. Записываем энергетический баланс

m*V1^2/2=m*V2^2/2+C*X^2/2                                             (9)

и отсюда находим, что скорость V2 будет 8,66 м/с. А вот с импульсным подходом для конечного решения ничего не получится, т.к. здесь мы видим, что сила удара в функции времени явно изменяется, поэтому, чтобы решать эту задачу с использованием импульсного подхода, надо знать эту зависимость, но мы ее можем получить только после аналитического решения этой задачи. Да, в работе [7] я получил такую зависимость F(t) и зависимость для текущей скорости V(t), решив дифференциальное уравнение описывающие процесс удара, поэтому просто для примера я могу определить скорость шара через 0,01 секунды с использованием импульсного подхода. Для этого надо составить импульсный баланс (12), вычислив импульс силы, как интеграл от F(t)*dt на интервале времени от нуля до 0,01 с.

F(t)= 1000*sin(100*t)                                                           (10)

V(t)= 10*cos(100*t)                                                              (11)

m*V1=m*V2+int(F(t)*dt, t=0..0,01)                                    (12)

1*10=1*V2+1000*(1-0,54)/100

Отсюда находим V2=5,4 м/с, что соответствует и скорости V(t) найденной по уравнению (11). При этом мы можем проверить это решение и с помощью моей программы Udar3m, где дифференциальное уравнение, описывающее удар двух шаров, решается численными методами (для этой задачи массу и жесткость второго шара надо взять очень большие). При этом данное конечное описание с использованием импульсного подхода имеет только гипотетическую возможность, т.е. его можно осуществить только если уже будет аналитическое решение этой задачи для F(t), но, если такое решение уже есть, то зачем тогда оно нужно это конечное описание с использованием импульсного подхода. Поэтому, в тех случаях, когда у нас внешняя сила, действующая на систему, изменяется во времени по неизвестному закону, то с использованием импульсного подхода возможно только текущее описание системы в приращениях, когда на малом интервале времени Δt можно считать, что сила не изменяется. Естественно, в приращениях возможно и текущее описание с использованием, как энергетического, так и силового и мощностного подходов, а вот дифференциальное описание мы можем получить только при использовании силового или мощностного подходов. При этом как описание в приращениях, так и дифференциальное описание позволяют именно смоделировать описываемые явления Природы и таким образом могут быть использованы и для более детального познания этих явлений Природы.

Что касается конечного описания явлений Природы с использованием импульсного и энергетического подходов, то этот вопрос широко освящен в учебниках, и останавливаться на нем я больше не буду. А вот что касается текущего описания, то его я освящу далее очень подробно, т.к. описание в приращениях вообще не освящено в учебниках и данная статья является первой публикацией по данному вопросу, а дифференциальное описание, хоть и дано в учебниках, но дано просто отвратительно, т.к. для этого пытаются притянуть за уши энергетический подход, который здесь совершенно не применим. Для дифференциального описания надо использовать или силовой подход или мощностной, т.к. нам надо описывать мгновенное (текущее) состояние системы в данный момент времени, а импульсный и энергетический подходы позволяют получить только интервальное описание системы в двух разных ее состояниях для двух моментов времени. Начнем подробное рассмотрение описания явлений Природы в приращениях с использованием различных подходов на примере нескольких конкретных задач. Сначала рассмотрим разгон обычной топливной ракеты, а потом рассмотрим разгон безтопливной ракеты, т.е. ракеты у которой масса не изменяется, а двигатель будет ионный и ракеты находятся далеко от других масс. Для этого введем следующие обозначения

m1 - масса ракеты до разгона (не изменяется у безтопливной ракеты).

Vgo - cкорость истечения газов или пыли из двигателя на стенде, т.е. относительно ракеты

P - развиваемая двигателем номинальная мощность

V1 - скорость ракеты до разгона

V2 - скорость ракеты в конце разгона.

mg1 - секундный расход топлива (газов или пыли)

mg= mg1*Δt - расход топлива (газа или пыли) за время разгона от скорости V1 до скорости V2

ΔV= V2-V1 - интервал изменения скорости ракеты при разгоне за время Δt

Vsr= (V1+V2)/2= V1+ΔV/2 - средняя скорость ракеты на этапе разгона

Vg= Vgo-Vsr - средняя скорость газов или пыли летящих от ракеты в другую сторону (или летящих вслед за ракетой, если Vgo<Vsr)

Δt - время разгона ракеты от скорости V1 до скорости V2

При использовании импульсного и энергетического подходов мы будем находить прирост импульса ракеты или ее энергии на интервале времени Δt, за который ее скорость увеличится на величину ΔV, или время Δt необходимое для увеличения скорости ракеты на величину ΔV. А при использовании силового и мощностного подходов мы будем находить среднюю силу, действующую на элементы системы, или подводимую к ним среднюю мощность на этих интервалах времени или скорости. При этом прирост импульса или энергии будем определять для ракеты, масса которой берется в конце заданных интервалов Δt или ΔV, а среднюю силу и среднюю мощность будем определять для ракеты, масса которой берется в середине интервала Δt или ΔV. При импульсном подходе у нас прирост импульса ракеты будет равен импульсу выброшенных за это время газов (закон сохранения импульса). При силовом подходе у нас средняя сила инерции ракеты будет равна средней силе давления газов на ракету и средней силе инерции массы сгоревшего топлива при торможении этой части топлива от скорости V1 до нуля (второй закон Ньютона в силовой интерпретации Эйлера). При энергетическом подходе у нас прирост энергии ракеты (без массы сгоревшего топлива), равен энергии выработанной двигателем плюс кинетическая энергия сгоревшего топлива, которая перешла к ракете за счет действия сил инерции при торможении этой части топлива от скорости V1 до нуля, и минус энергия улетевших газов. А при мощностном подходе у нас в левой части будет средняя мощность, пошедшая на разгон ракеты, а в правой части будут те же составляющие, что и для энергии, но для средней мощности.

(m1-mg1*Δt)*V2 - m1*V1 = mg1*Δt *Vg                                                             (13-1)    импульсный

(m1-mg1*Δt /2)*ΔV/Δt = mg1*Vg + mg1*Vsr = mg1*Vgo                                  (13-2)     силовой

(m1-mg1*Δt /2)*Vsr*ΔV/Δt = P + mg1*Vsr^2/2 - mg1*Vg^2/2                           (13-3)     мощностной

(m1-mg1*Δt)*(V2^2-V1^2)/2 = P*Δt + mg1*Δt*V1^2/2 - mg1*Δt*Vg^2/2        (13-4)     энергетический

Отсюда, используя прирост скорости, т.е. задавая V1 и ΔV или V1 и V2 находим время Δt, которое необходимо, чтобы увеличить скорость ракеты от V1 на величину ΔV.

Δt = m1 * ΔV  / (mg1 * V2 + mg1 * Vg)                                                                        импульсный

Δt = 2 * m1 * ΔV / (mg1 * ΔV + 2 * mg1 * Vgo)                                                           силовой

Δt = 2 * m1 * Vsr * ΔV / (2 * P + mg1 * Vsr * ΔV + mg1 * Vsr ^ 2 - mg1 * Vg ^ 2)   мощностной

Δt = m1 * (V2 ^ 2 - V1 ^ 2) / (2 * P + mg1 * (V2 ^ 2 - Vg ^ 2))                                     энергетический

Как видим, формулы получились разные, но, как я покажу ниже, ответ они дают один и тот же. А теперь давайте перепишем наши формулы импульсного, силового и мощностного балансов так, чтобы можно было по приращению времени Δt  находить приращения скорости ΔV. При этом для мощностного баланса я сначала привожу запись, когда не расшифровываю значения Vsr и Vg в приращениях ΔV, т.к. после преобразований правая часть значительно упрощается. Находим из этих трех уравнений выражение для ΔV и видим, что ответ получается один и тот же (14). А для энергетического баланса решение получается неоднозначное, т.к. получается квадратное уравнение, которое имеет два корня и преобразования получаются очень сложные, поэтому я не стал их выполнять вручную и перепоручил это пакету символьных вычислений Maple. Ниже я и привожу получившиеся выражения для двух значений ΔV, но не думаю, что кому-то понравится это решение, которое гораздо сложнее первых трех.

(m1-mg1* Δt)*(V1+ΔV) - m1*V1 = mg1*Δt*(Vgo-V1- ΔV/2)                           импульсный

(m1-mg1*Δt/2)*ΔV/Δt = mg1*Vg + mg1*Vsr = mg1*Vgo                                  силовой

(m1-mg1*Δt/2)*Vsr*ΔV/Δt = mg1*Vgo^2/2 + mg1*(Vsr^2 - (Vgo-Vsr)^2)/2   

(m1-mg1*Δt/2)*ΔV/Δt = mg1*Vgo                                                                        мощностной

ΔV = mg1*Δt*Vgo / (m1 - mg1*Δt/2)                                                 (14)               

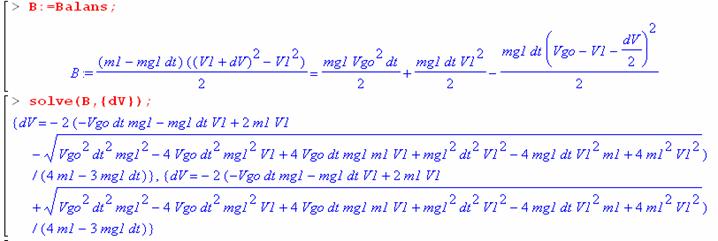
При этом обращаю Ваше внимание, что описание явлений Природы в приращениях хоть и является аналогом дифференциального описания, но не может быть использовано для получения дифференциальных уравнений из этих уравнений в приращениях. Это принципиально разные описания, хотя формально получаются очень похожие формулы. Сравните две нижеприведенных формулы для среднего ускорения (15) и для мгновенного ускорения (16). И даже, если в формуле (15) заменить Δt/2 для ускорения в середине интервала времени на Δt для ускорения в конце этого интервала времени, то все равно это будет не формула (16), а на примере разгона безтопливной ракеты я покажу, что там получаются еще сильнее отличающиеся друг от друга формулы для расчета среднего ускорения и мгновенного. И, чтобы закончить с разгоном топливной ракеты, я приведу и получающиеся при аналитическом решении уравнения (16) формулы для скорости ракеты (17) и пройденного пути (18) в функции времени, а также для времени необходимого для увеличения скорости ракеты на величину ΔV (19). Напоминаю, что формулы для скорости и силы в функции пройденного пути могут существенно отличаться от формул в функции времени и далее на графиках я это продемонстрирую.

ΔV/Δt = mg1*Vgo / (m1 - mg1*Δt / 2)                                             (15)          среднее ускорение

dV/dt= mg1*Vgo / (m1 - mg1*t)                                                       (16)          мгновенное ускорение

V(t) = V1 - Vgo * Ln(1 - mg1*t / m1)                                               (17)

S(t) = V1*t + Vgo * ((m1 / mg1 - t) * Ln(1 - mg1*t / m1) + t)         (18)

t(ΔV) = m1*(1 - e^(-ΔV/Vgo)) /mg1                                                 (19)

А теперь давайте посмотрим, что же у нас получается по приведенным формулам в приращениях и сравним полученные значения с аналитическим решением дифференциального описания. Используя  уравнения (13-1)...(13-4) для расчета Δt мы можем задавать начальную скорость V1 и интервал изменения скорости ΔV, т.е. приращение в приемлемых пределах, чтобы задать скорость V2, а потом находить интервал времени Δt1, который необходим, чтобы увеличить скорость V1 на ΔV. А затем мы задаем новую начальную скорость V1+ΔV и конечную V1+2*ΔV и находим Δt2 и т.д. По ходу вычислений мы можем все интервалы Δt суммировать и находить зависимость времени разгона до разной скорости t(V) или в табличном виде или в графическом. А суммируя отрезки пути ΔS=Vsr*Δt находим и зависимость S(V). Хотя, точно также, используя получающиеся данные, можно построить и зависимость V(t) и S(t). А можно задавать начальное время t1 и начальную скорость V1, потом, задавая приращение времени Δt, находить по формуле (14), какое получится приращение скорости ΔV1. Затем задать новое начальное время t1+Δt и новую начальную скорость V1+ΔV1, а потом найти новое приращение скорости ΔV2 на следующем интервале времени Δt и т.д. Точно также, суммируем все получающиеся по ходу вычислений ΔV и находим зависимость V(t) и S(t) или t(V) и S(V).

А ниже я привожу данные по времени разгона, которые у меня получаются при разгоне от V1=0 до V2=380 м/с, как по аналитическому решению дифференциального описания (19), так и в приращениях скорости при использовании различных уравнений (13-1)...(13-4), которые у меня получились при различных подходах решения задачи. При этом в расчете использовались данные m1=1000 кг, P=100 кВт, Vgo=200 м/с, а решение в приращениях велось с шагом ΔV=0,001 м/с.

t=170,086 276 155 473 - аналитическое решение

t=170,086 276 155 793 - импульсный подход

t=170,086 276 155 793 - силовой подход

t=170,086 276 155 793 - мощностной подход

t=170,086 276 154 408 - энергетический подход

Расхождения в последних значащих цифрах, которые дает моя программа (у меня используется 8-и битное представление данных, т.е. получается только 15-ть значащих цифр) объясняется не только наличием шага решения, но и из-за округлений в последней значащей цифре для различных переменных при любом шаге решения, т.к. по ходу вычислений после каждого шага суммируются полученные приращения, то и  все эти округления тоже суммируются. Но, как видим, полученная точность решения более чем удовлетворительная и, если не нужна такая высокая точность решения в приращениях, то можно увеличить шаг изменения скорости, что значительно ускорит решение задачи. Такая же хорошая точность решения в приращениях будет и при использовании формулы (14), когда мы будем с шагом Δt=0,001 секунды задавать различные моменты времени и будем находить приращения скорости ΔV. Полученный результат для времени разгона 170 секунд, когда начальная скорость задается равной нулю, мы сравним с аналитическим решением по формуле (17).

V=379,423 996 977 176 - аналитическое решение

V=379,423 996 968 305 - решение в приращениях

А ниже я привожу графики, получающиеся по найденным зависимостям для аналитического решения и решения в приращениях, которые визуально не отличаются друг от друга, т.к. дают примерно одинаковые результаты. На первых двух графиках развертка идет по Vgo и Vsr, а на нижнем по t. При этом в расчете использовались данные m1=1000 кг, P=100 кВт, Vgo=200 м/с, V1=310 м/с и V2=320 м/с. Если мы строим графики в функции от Vgo или Vsr, то мы на каждом приращении задаем эти значения с заданным шагом от начального (Vn) до конечного значений (Vk) при ΔV=V2-V1=10 м/с. А, если у нас развертка графиков по времени, то мы можем задавать с заданным шагом или приращения скорости ΔV или приращения времени Δt (выбрать в рамке <задать>), а величину приращений задаем в окошке <с шагом>.

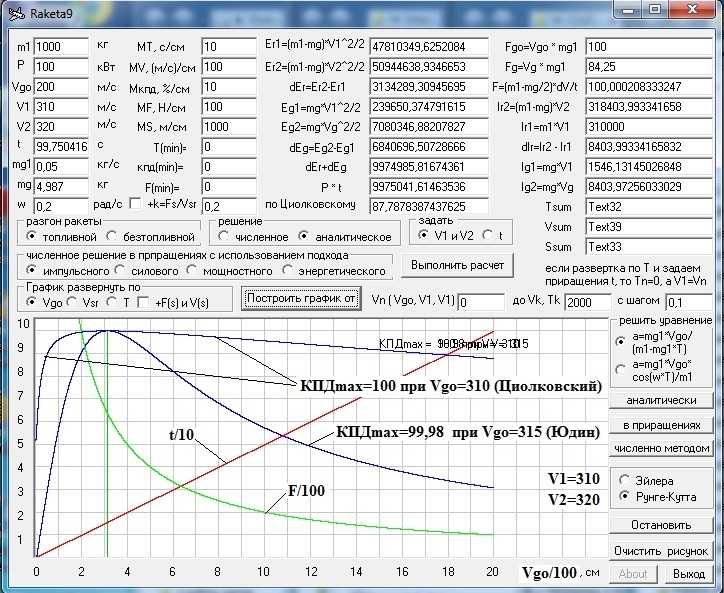
Рис. 1. Графики изменения времени разгона топливной ракеты t при ее разгоне с 310 до 320 м/с, возникающей при этом силы F, ускоряющей ракету, и КПД движителя в функции от изменения скорости газов относительно ракеты. Скриншот программы Raketa9.

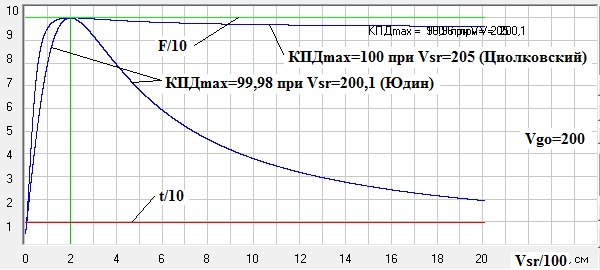
Рис. 2. Графики изменения времени разгона топливной ракеты t при ее разгоне на ΔV=10 м/с, возникающей при этом силы F, ускоряющей ракету, и КПД движителя в функции от средней скорости ракеты Vsr, определяемой на интервале ΔV, при скорости газов относительно ракеты Vgo=200 м/с. Скриншот программы Raketa1.

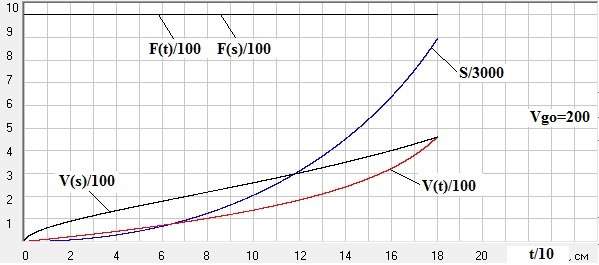
Рис. 3. Графики изменения текущей скорости топливной ракеты V(t) и V(s), пройденного ею пути S(t) и возникающей при этом силы F(t) и F(s), ускоряющей ракету, в функции времени V(t) и F(t) и в функции пройденного пути V(s) и F(s) при скорости газов относительно ракеты Vgo=200 м/с (здесь разгон идет от Vn=0). Скриншот программы Raketa1.

Как наглядно видно из этих графиков, КПД движителя ракеты (реактивные двигатели являются одновременно и движителями) имеет для различных режимов разгона строго определенный максимум и он равен 100%. Вот только аналитическое выражение для КПД, полученное Циолковским [24], является ошибочным, т.к. правильно определять КПД движителя надо по формуле (20). Кстати, и вывод аналитической формулы для скорости ракеты, сделанный Циолковским с использованием импульсного подхода [24], является не корректным, хотя сама формула (17), приведенная им, и является правильной. И, исходя из этой формулы, конечная скорость ракеты теоретически ничем не ограничена и при приближении массы ракеты к нулю растет до бесконечности. Поэтому на рис. 3, исходя из технических соображений, приведен график только для скорости ракеты при времени разгона до 180 секунд, т.е. до времени, когда масса ракеты составила 10% от ее начальной массы.

КПД=ΔEr / (P*Δt+Eg1)    (20)

Здесь ΔEr=(m1-mg1*Δt)*V2^2/2 - m1*V1^2/2 - прирост кинетической энергии ракеты без массы сгоревшего топлива, P*Δt - энергия выработанная двигателем за время Δt, а Eg1=mg1*Δt*V1^2/2 - кинетическая энергия топлива, сгоревшего за время Δt

А теперь давайте составим балансы в приращениях для разгона безтопливной ракеты. Здесь у нас принципиальным отличием от обычной топливной ракеты будет то, что масса ракеты не будет изменяться, т.к. в качестве топлива мы будем использовать космическую пыль, которую будем собирать по ходу движения ракеты. При этом у нас конструкция пылесборников будет такая, что при разной скорости ракеты в одну секунду будет собираться одно и то же количество пыли mg1. И из пылесборников дозатором в ионный двигатель будет подаваться в одну секунду тоже постоянное количество пыли mg1 для того, чтобы мощность двигателя оставалась постоянной. А энергия на ионизацию пыли и на ее разгон в электрическом поле будет потребляться или от солнечных батарей или от ядерной установки и можно считать, что масса ракеты не изменяется. Давайте, так же, как и для топливной ракеты, составим четыре уравнения балансов при различных подходах. Сначала для задания приращения ΔV и нахождения нужного для этого значения Δt, а потом наоборот.

m1*(V2 - V1) = mg1*Δt*Vg                                                                    (21-1)             импульсный  

m1*ΔV/Δt = mg1*Vg                                                                                (21-2)             силовой   

m1*Vsr*ΔV/Δt = P - mg1*Vg^2/2 - mg1*Vsr^2/2                                   (21-3)             мощностной  

m1*(V2^2-V1^2)/2 = P*Δt - mg1*Δt*Vg^2/2 - mg1*Δt*Vsr^2/2            (21-4)             энергетический

Основным отличием этих уравнений от уравнений (13-1)...(13-4) будет то, что здесь, как это наглядно видно из силового баланса, у нас сила давления газов (ионизорованной пыли) на ракету будет не mg1*Vgo, а mg1*Vg. Это связано с тем, что здесь у нас будет именно та сила давления, которая и должна быть, т.к. теперь у нас в балансе отсутствует сила инерции сгораемого топлива, которая давала дополнительную силу при уменьшении массы топливной ракеты. Хотя, на самом деле, эта сила будет присутствовать, т.к. прежде, чем пыль будет выброшена со скоростью Vgo относительно ракеты, ее скорость также будет уменьшаться от V1 до нуля и масса ракеты будет уменьшаться на величину mg1, но у нас за счет того, что мы ежесекундно в пылесборники будем собирать тоже mg1 кг пыли, масса ракеты уменьшаться не будет. Но у нас появится сила сопротивления движению ракеты, которая в точности будет равна силе инерции возникающей при торможении пыли от V1 до нуля прежде, чем она со скоростью Vgo относительно ракеты будет выброшена из двигателя. Поэтому, в приведенных выше уравнениях должны присутствовать и составляющие, которые я привожу ниже, но, т.к. они взаимно сокращаются, я их не стал записывать.

- mg1*Δt *Vsr + mg1*Δt*Vsr                           импульсный

- mg1*Vsr + mg1*Vsr                                       силовой

- mg1*Vsr^2/2 + mg1*Vsr^2/2                         мощностной  

- mg1*Δt*Vsr^2/2+mg1*Δt*Vsr^2/2                энергетический 

При этом, как Вы заметили, у нас в мощностном и энергетическом балансах не просто пропали, как в силовом балансе, члены, которые отражали мощность и энергию от действия сил инерции части сгораемого топлива, но и появилась новая составляющая, а именно мощность и энергия, затраченные на нагрев пыли при ее неупругом ударе о пылесборник. А вот, что касается импульсного подхода, то на его балансе изменения во влиянии сил инерции сгораемого топлива никак не отразились, т.к. этот подход для замкнутой системы никак не связан ни с силами, ни с энергиями и является в этом смысле вещью в себе. А, т.к. здесь у нас пыль и рассматривается, как часть системы, но импульс пыли первоначально был равен нулю, то от учета этого нуля здесь нечего и не изменится. Вообще то, считается, что импульсный подход не применим при диссипации энергии, но это справедливо только в том случае, когда диссипация энергии происходит при проскальзывании элементов системы относительно элементов окружающей среды, например, при движении ракеты в сопротивляющейся среде и то при решении задачи в конечном виде, а в приращениях возможно решение и в этом случае. Но эти тонкости импульсного подхода я рассмотрю ниже, а сейчас давайте закончим с разгоном безтопливной ракеты и найдем значения Δt из уравнений (21-1)... (21-4).

Δt  = m1*ΔV / (mg1*Vg)                                                             импульсный

Δt = m1*ΔV / (mg1*Vg)                                                              силовой

Δt = 2*m1*ΔV*Vsr / (2*P - mg1*Vsr^2 - mg1*Vg^2)               мощностной

Δt = m1*(V2^2 - V1^2) / (2*P - mg1*Vsr^2 - mg1*Vg^2)         энергетический

Точно также найдем из уравнений (21-1)... (21-4) и приращеня ΔV в функции от заданного значения Δt. И здесь так же, как и ранее для топливной ракеты, выразим Vsr и Vg через V1 и ΔV. Здесь тоже для расчета ΔV при всех подходах получается одна формула (22), а также и при применении энергетического подхода получается неоднозначное решение и я его не привожу, а для мощностного подхода также привожу вывод с промежуточными выкладками.

m1*(V1 + ΔV - V1) = mg1*Δt*(Vgo - V1 - ΔV/2)                       импульсный   

m1*ΔV/Δt = mg1*(Vgo - V1 - ΔV/2)                                            силовой   

m1*Vsr*ΔV/Δt = P - mg1*(Vsr^2 - (Vgo-Vsr)^2)/2                     мощностной

m1*Vsr*ΔV/Δt = mg1*Vgo*Vsr - mg1*Vsr^2

m1*ΔV/Δt = mg1*Vgo - mg1*(V1+ ΔV/2)

ΔV = mg1*Δt*(Vgo - V1) / (m1 + mg1*Δt / 2)                           (22)   для расчета среднего ускорения    

ΔV/Δt = mg1*(Vgo - V1) / (m1 + mg1*Δt )                                (23)    ускорение в конце приращения

dV/dt= mg1*(Vgo-V(t)) / m1                                                       (24)    мгновенное ускорение

V(t) = V1 + (Vgo-V1)*(1 - e^(-mg1*t / m1))                              (25)

S(t) = Vgo*t + (Vgo-V1)*m1*(e^(-mg1*t /m1) - 1) / mg1          (26)

t(ΔV) = m1*Ln((Vgo-V1) / (Vgo-V2)) / mg1                              (27)

Здесь так же, как и у топливной ракеты, формула в приращениях для расчета среднего ускорения (22) не подходит для получения дифференциального уравнения, где определяется мгновенное ускорение (24), даже, если мы заменим в формуле (22) Δt/2 для ускорения в середине интервала времени на Δt для ускорения в конце этого интервала времени. Мы видим, что получающаяся при этом формула (23) уже очень заметно отличается от формулы дифференциального описания (24), т.е. это принципиально разные формулы. На особенностях получения дифференциальных уравнений с использованием различных подходов я остановлюсь чуть ниже, а сейчас давайте, так же, как и для топливной ракеты, сравним точность решений в приращениях с данными, получающимися по аналитическим зависимостям, вытекающим из формулы (24). Ниже я привожу данные по времени разгона, которые у меня получаются при разгоне от V1=0 до V2=180 м/с, как по аналитической формуле (27), так и в приращениях скорости при использовании различных уравнений (21-1)...(21-4). При этом в расчете использовались данные m1=1000 кг, P=100 кВт, Vgo=200 м/с, а решение в приращениях велось с шагом ΔV=0,001 м/с.

t=460,517 018 598 809 - аналитическое решение

t=460,517 018 578 182 - импульсный подход

t=460,517 018 578 182 - силовой подход

t=460,517 018 578 182 - мощностной подход

t=460,517 018 578 182 - энергетический подход

Точно так же хорошая точность решения в приращениях будет и при задании приращений времени и расчета получающихся приращений скорости по формуле (22), когда мы будем с шагом Δt=0,001 с задавать различные моменты времени и будем находить приращения скорости ΔV. Конкретно для времени разгона 460 секунд, когда начальная скорость равна нулю, мы при решении в приращениях и по аналитической формуле (25) получим.

V=179,948 231 255 439 - аналитическое решение

V=179,948 231 255 371 - решение в приращениях

А сейчас давайте по формулам (21-1)... (21-4) построим графики, чтобы, во-первых, убедиться, что результат по всем формулам получается один и тот же (как видим на рисунках графики совпали) и при этом соответствует расчету по формуле (27) для аналитического решения (и этот график тоже совпал с предыдущими), а во-вторых, чтобы посмотреть как измененяются показатели функционирования безтопливной ракеты при различных режимах ее разгона. На первых двух графиках развертка идет по Vgo и Vsr, а на нижнем по t, но здесь у нас в последнем случае в конце графика получается очень мало точек, т.к. скорость безтопливной ракеты со временем асимптотически приближается к Vgo и поэтому, задавая даже маленькое значение приращения ΔV, мы получаем очень большое приращение Δt. Поэтому, такой график для безтопливной ракеты лучше строить задавая при расчете Δt и находя приращения ΔV по формуле (22). В расчетах, также, как и при разгоне топливной ракеты, начальные данные для расчета были такими m1=1000 кг, P=100 кВт, Vgo=200 м/с, V1=310 м/с и V2=320 м/с. При этом, так же, как и на графиках разгона топливной ракеты, если мы строим графики, например, в функции от Vgo, то мы на каждом приращении задаем эти значения с заданным шагом от начального до конечного заданных значений.

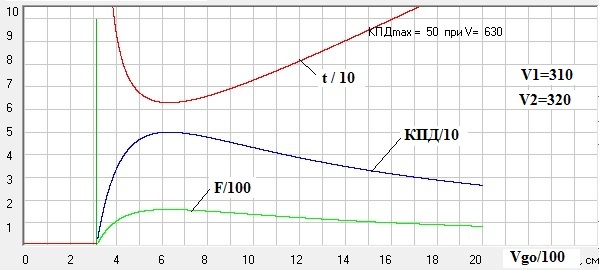
Рис. 4. Графики изменения времени разгона безтопливной ракеты t при ее разгоне с 310 до 320 м/с, возникающей при этом силы F, ускоряющей ракету, и КПД движителя в функции от изменения скорости газов относительно ракеты. Скриншот программы Raketa1.

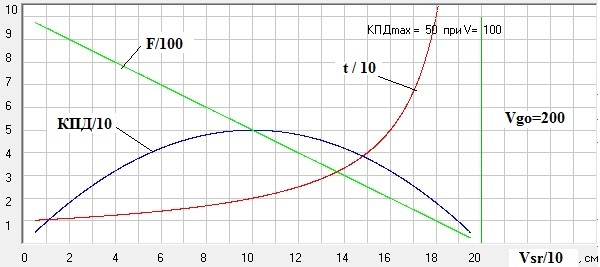
Рис. 5. Графики изменения времени разгона безтопливной ракеты t при ее разгоне на ΔV=10 м/с, возникающей при этом силы F, ускоряющей ракету, и КПД движителя в функции от средней скорости ракеты Vsr, определяемой на интервале ΔV, при скорости газов относительно ракеты Vgo=200 м/с. Скриншот программы Raketa1.

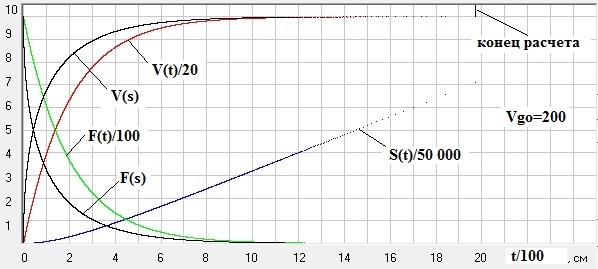
Рис. 6. Графики изменения текущей скорости безтопливной ракеты V(t) и V(s), пройденного ею пути S(t) и возникающей при этом силы F(t) и F(s), ускоряющей ракету, в функции времени V(t) и F(t) и в функции пройденного пути V(s) и F(s) при скорости газов относительно ракеты Vgo=200 м/с (здесь разгон идет от от Vn=0). Скриншот программы Raketa1.

Из этих графиков мы так же видим, что КПД движителя ракеты имеет для различных режимов разгона строго определенный максимум и он равен 50%. Это объясняется тем, что теперь у нас кинетическая энергия топлива, сгораемого за время Δt, не передается ракете, т.к. точно такая же знергия затрачивается на разгон этой же массы топлива (пыли) от нуля до скорости ракеты прежде, чем потом эта пыль будет выброшена из ракеты в противоположную сторону, а, кроме того, у нас точно такая же энергия затрачивается еще и на нагрев пыли при ее неупругом столкновении с летящей ракетой. По этому, хотя у нас теперь в формуле (20) энергия Eg1 и равна нулю, но прирост энергии ракеты будет значительно меньше, а конкретно он будет ΔEr=m1*(V2^2-V1^2)/2. И теперь у нас разгон ракеты будет только в том случае, если конечная скорость безтопливной ракеты V2 будет меньше скорости выброса пыли Vgo и при приближении V2 к Vgo прирост скорости ΔV стремится к нулю и, следовательно, скорость ракеты теперь ограничена Vgo. Поэтому на рис. 6, когда мы при расчете в приращениях задавали ΔV и находили Δt, мы видим, что при приближении V2 к Vgo у нас при тех же значениях ΔV получаются все большие и большие значения Δt . А вот, если мы будем задавать приращения Δt и находить приращения ΔV, то мы наоборот получим очень большое количество точек в конце графика при практически одинаковой скорости.

Ну и прежде чем закончить с рассмотрением разгона наших ракет я бы хотел на этих же примерах рассмотреть два заблуждения, которые существуют в современной (официальной) науке. Первое это то, что при наличии диссипации в системе нельзя для описания этих систем применять импульсный подход, и второе это то, что никакое тело нельзя разогнать до скорости больше скорости света. Что касается первого заблуждения, то здесь сама диссипация энергии не имеет к этому никакого отношения и мы можем сделать, например, конечное описание удара двух абсолютно неупругих шаров, что в учебниках и делается или описать в приращениях разгон безтопливной ракеты при нагреве пыли при ударе, что мы сделали выше. Но здесь у нас была одна особенность - диссипация энергии в обоих случаях происходила вследствие взаимодействия тел входящих в описываемую нами систему и поэтому это никак не влияло на описание этих систем с использованием импульсного подхода. А вот если диссипация энергии будет происходить при взаимодействии тел входящих в описываемую систему и не входящих в нее, то здесь уже в описании появятся силы трения. Но при импульсном подходе мы можем учитывать только силы зависящие от времени, а силы трения, как и любые другие силы, зависят только от координат и скоростей и поэтому мы можем их учесть только в частном случае, когда силы трения не зависят от времени. Например, при скольжении груза по наклонной плоскости, когда сила трения остается примерно постоянной.

А в тех случаях, когда силы зависят от координат или скоростей, нам, чтобы их учесть в конечном описании, надо найти зависимость того, как они будут изменяться со временем и такой пример я рассмотрел выше при ударе упругого шара в стену, где использовал уже найденную ранее зависимость силы удара в функции от времени. Точно также, уже решив конкретную задачу с использованием другого подхода и найдя зависимость изменения сил трения в функции времени, мы можем потом решить эту задачу в конечном описании и с использованием импульсного подхода. Но это будет уже повторное решение, а нам надо сделать первое решение с использованием импульсного подхода. И такое решение возможно и в нашем случае, т.е. при внешней диссипации энергии, но для этого нам надо сделать с использованием импульсного подхода описание в приращениях. Здесь у нас на малых интервалах времени мы можем считать силы трения неизменными и поэтому можем применять импульсный подход.

 Давайте рассмотрим описание с использованием импульсного подхода разгон топливной ракеты, когда она у нас движется в среде оказывающей сопротивление движению ракеты с силой F=k*V, где k- коэффициент пропорциональности при линейном жидкостном сопротивлении, а V это скорость ракеты. Описанием этого процесса в приращениях будет импульсный баланс (28) для нахождения малых приращений Δt или ΔV. Например, приращение скорости ΔV при заданном приращении Δt определится как (29). И, чтобы доказать корректность импульсного подхода для описания этого процесса, я проверю точность этого решения по аналитическому решению для скорости (31), которое получено из дифференциального описания при силовом подходе (30). Ниже я привожу получившуюся скорость ракеты для времени разгона 170 секунд, которая получается при решении задачи описанной в приращениях (29) с шагом Δt=0,001 секунды. Параметры ракеты были те же, что я использовал в расчетах выше, но теперь еще добавилось сопротивление среды с k=0,2 Н*с/м. Как видим, погрешность в решении такая же, как и при отсутствии трения (в 11-м знаке), т.е. импульсный подход для описания явлений Природы в приращениях применим и в том случае, когда у нас есть диссипация энергии из системы при ее взаимодействии с элементами не входящими в систему.

(m1-mg1*Δt)*(V1+ΔV) - m1*V1 = mg1*Δt*(Vgo-V1- ΔV/2) - Δt*k*(V1 + ΔV/2)        (28)

ΔV = (mg1*Δt*Vgo - k*Δt*V1) / (m1 - mg1*Δt/2 + k*Δt/2)                                            (29)       

dV/dt= (mg1*Vgo - k*V) / (m1 - mg1*t)                                                                            (30)

V(t) = (mg1*Vgo/k) * [1 - (1 - mg1*t/m1)^(k/mg1)]                                                          (31)

V=365,385 087 515 467 - аналитическое решение

V=365,385 087 507 219 - решение в приращениях

А теперь давайте рассмотрим второе заблуждение, т.к., например, теоретически ракета с ионным двигателем может разогнаться до скорости больше скорости света, но для этого надо, чтобы чисто технически на первом этапе разгона мы использовали безтопливную ракету, а на втором этапе топливную. Ведь, как следует из графиков на рис.2, у нас время разгона топливной ракеты на величину ΔV=10 м/с не зависит от текущей скорости ракеты и остается постоянным 9,75 с. Таким образом, все упирается только в то, чтобы хватило топлива, т.е. в нашем случае просто пыли. При этом запас пыли для второго этапа разгона может быть, как запасен изначально, так и запасен на первом этапе разгона, когда мы будем собирать пыли больше, чем будем выбрасывать, что предпочтительнее. Разгонять в ионном ускорителе частички пыли мы можем только до скорости меньше скорости света, т.к. до скорости света мы их не можем разогнать теоретически вследствие того, что разгонять мы их будем в электрическом поле, а скорость распространения этого поля равна скорости света. Таким образом, на первом этапе мы можем разогнать ракету только до скорости хоть и немного, но меньше, чем скорость света. А вот при разгоне на втором этапе топливной ракеты ее конечная скорость ничем не ограничена, кроме запаса пыли, который ограничивает максимальное время разгона, поэтому здесь мы сможем разогнать ракету до скорости больше скорости света, если нам хватит этого запаса пыли.  

                                     особенности метода дифференциального описания систем

А сейчас давайте рассмотрим возможности различных подходов (импульсного, силового, мощностного и энергетического) для получения текущего дифференциального описания явлений Природы. Здесь сразу отпадают импульсный и энергетический подходы, т.к. нам надо получить уравнение описывающее текущее (мгновенное) поведение системы, а эти подходы могут дать описание только используя значения импульса и энергии в начальном и конечном состояниях системы. Мне могут возразить, что энергетический подход с использованием лагранжиана L=T-U (3) позволяет получить дифференциальные уравнения для описания системы. Но здесь мы имеем энергетический подход не в чистом виде, а его суррогат, т.к. по сути используется силовой подход, а все эти манипуляции с кинетической энергией системы нужны только для того, чтобы получить выражение для силы инерции действующей по обобщенным координатам и, если у нас имеется и потенциальная энергия, то и для силы от взаимодействия системы с этим полем. А потом уже к этим двум силам, если необходимо, добавляются и другие обобщенные силы, действующие на эту систему, т.е. используется силовой подход, т.к. при энергетическом подходе никаких сил не должно быть, как это у нас и было при описании процесса движения двух ракет с использованием энергетического подхода.

А, если мы производим описание явлений Природы не в обобщенных координатах, а в обычной декартовой системе координат, то нет никакой необходимости в манипуляциях с энергиями в обобщенных координатах и мы можем сразу, используя силовой подход Эйлера (33), записать, что сила инерции по каждой из осей координат равна силе взаимодействия нашего тела с потенциальным полем. А потом, используя этот же силовой подход, добавлять к этим двум силам, если необходимо, и другие силы, действующие на тела системы, поведение которой мы описываем. При этом, если мы будем описывать явления Природы в декартовой системе координат, то манипуляции Гамильтона (3) с его лагранжианом упростятся до выражения (32), т.к. кинетическая энергия будет зависеть только от скорости, а потенциальная энергия только от координат и поэтому отпадает необходимость проводить все манипуляции Эйлера для получения уравнений экстремалей в геометрических задачах, которые Лагранж тупо перенес на задачи механики. Но, я думаю, что многие будут поставлены в тупик, если попробуют получить с использованием даже этих упрощенных манипуляций (32) дифференциальное уравнение для описания движения топливной ракеты. Хотя здесь у нас не будет ни потенциальной энергии, ни внешних сил, действующих на систему, а кинетическая энергия системы у нас будет состоять только из энергии ракеты и энергии газов.

d(dL/dVr)/dt - dL/dR =0                                            (3)

d(dT/dVr)/dt + dU/dR =0                                           (32)

m*d2R/dt2 - Fr = 0                                                     (33)

К тому же, надо отметить, что описание систем в обобщенных координатах имеет практический смысл только для самых элементарных систем, которые и рассматриваются в учебниках, и к тому же при этом и информации от такого решения мы получаем самый минимум, который нас не устраивает при решении практических задач. А само описание в обобщенных координатах, даже для простейших реальных систем, получается просто умопомрачительное, поэтому при решении реальных задач никто, имеющий хоть пару извилин, не будет использовать энергетическо-геометрический подход Лагранжа с его обобщенными координатами.  И, чтобы в этом убедится, я рассмотрю ниже описание с использованием энергетическо-геометрического подхода Лагранжа обычного кривошипно-шатунного механизма. А вообще-то, с использованием манипуляций с лагранжианом мы не можем описать ни одной механической системы, т.к. в реальных условиях в любых системах всегда будут силы трения, т.е. будет диссипация энергии, а в этом случае эти манипуляции нельзя использовать, т.к. в этом случае нельзя применять ПНД, из которого они и вытекают.

Но это нисколько не смущает математико-физиков и Ландау, который является ярым сторонником Лагранжа, и на стр. 97 [2] своего культового для СССР учебника просто заявляет, что «Процесс движения в этих условиях уже не является чисто механическим процессом». Таким образом, если механическая система не описывается функцией Лагранжа, то для Ландау это уже не механика (правда он употребляет термин не классическая механика). Но позвольте, мы не знаем ни одной механической системы, где бы отсутствовало трение, т.е. получается, что Механика Ландау не имеет никакого отношения к реальной механике. Единственная область, где, как пишет Фейнман, отсутствует трение это механика микромира и, таким образом, получается, что вся Механика Ландау нужна только для квантовой механики. Хотя и здесь не все так однозначно, т.к., например, тормозное излучение электрона, которое, по сути, является той же диссипацией энергии, никто вроде не отрицает. И получается, что и в квантовой механике Механика Ландау не применима. А тогда вообще не понятно о механике для какой галактики он написал свой учебник. Но Ландау пытается все же обосновать то, что его Механика нужна физике именно для нашей галактики и вот, что он пишет.

 «Если при скольжение трение настолько мало, что им можно вовсе пренебречь, то поверхности тел называются абсолютно гладкими. Напротив, если свойства поверхности допускают лишь чистое качение тел без скольжения, а трением при качение можно пренебречь, то поверхности называются абсолютно шероховатыми.

В обоих случаях силы трения не фигурируют явным образом в задаче о движении тел, и по этому задача является чисто механической. Если же конкретные свойства трения существенны для движения, то последнее не является уже чисто механическим процессом (ср. §25).»

А теперь упритесь большим пальцем правой руки в абсолютно гладкий стол и быстро проведите рукой справа налево. У вас возникнут автоколебания большого пальца, но Ландау не научит Вас решать эту элементарную механическую задачку потому, что по его классификации это не механическая задача. Да, Ландау в совершенстве владел интегральным и дифференциальным исчислениями и здесь рядом с ним можно поставить разве что Эйлера и Лагранжа, но объявлять механикой только те явления, которые описываются дифференциальными уравнениями, вытекающими из ПНД, т.е. обязательно без трения, и которые он может решить, в корне не верно.

При этом, как ни странно, он рассматривает и движения тел в среде, т.е. с диссипацией энергии, и отводит им шесть параграфов в своей Механике (25...30), хотя и не считает такие задачи механическими. А объяснение здесь простое.  Для частного случая, когда сопротивление среды пропорционально скорости в первой степени, оказывается дифференциальные уравнения для описания таких систем, хотя и не получаются из его любимого ПНД, но они получаются с помощью манипуляций, которые он придумал для диссипативной функции, линейным а в этом случае он их может решить и, следовательно, этому он и будет учить своих читателей. Таким образом, и трение, по большому счету, не является препятствием для отнесения таких систем к механическим, т.е. механикой у Ландау являются только те процессы при описание которых он может продемонстрировать свои математические способности. А вот, когда он рассматривает различные механические системы, где всегда присутствует в основном сухое трение (или скольжения или качения), то он на стр.162 объявляет эти системы уже точно не механическими (такие уравнения не решаются аналитически) и поэтому дальше он будет учить читателей решать только механические задачи, т.е. получается что он будет учить решать приблизительные (учебные) механические задачи, где сухого трения нет. Отсюда можно сделать вывод о том, что то, что выгодно лично Ландау, то правильно, а то, что не выгодно, это не правильно, т.е. в Механике Ландау действуют уже не законы точных наук, а политические законы, где то, что выгодно, например, Америке, это правильно, а то, что не выгодно, это не правильно.

А теперь давайте рассмотрим описание с использованием энергетическо-геометрического подхода Лагранжа обычного кривошипно-шатунного механизма (КШМ), изображенного на рис. 7. Здесь у нас только одна обобщенная координата - угол поворота кривошипа. Я не буду давать вывод дифференциального уравнения, т.к. он еще более громоздкий, чем получившийся ответ, и приведу только дифференциальное уравнение для ускорения угла поворота кривошипа.     

Рис. 7. Расчетная схема кривошипно-шатунного механизма для описания по обобщенным координатам.

Но, кого интересуют подробности вывода этого дифференциального уравнения, могут ознакомиться с этим в файле krivo1 (или в формате .mws для работы с математическим пакетом Maple 9.5 или в формате .html для просмотра в браузере). Естественно, студентов такими уравнениями не пугают и поэтому в учебниках, например, у Ландау дают вывод дифференциальных уравнений для самых простеньких систем. Но для инженеров-механиков все же кое-что дают и по таким сложным системам, как КШМ, хотя и в этом случае дают упрощенный вывод, т.е. с различными упрощениями, как, например, здесь [29]. Но и в этом случае получается мало пригодное для практического использования уравнение (34).

(34)

где : Jp -  приведенный момент инерции системы; Kl, Kj - коэффициенты ( Kl = R / L ); R - радиус кривошипа; L - длина шатуна; M - момент сопротивления приложенный к кривошипу (маховику); P1 , P2 , P3 - соответственно вес кривошипа, шатуна и поршня; g - ускорение свободного падения.

А, кого интересуют подробности вывода и этого упрощенного дифференциального уравнения, могут ознакомиться с этим в файле krivo2 (или в формате .mws для работы с математическим пакетом Maple 9.5 или в формате .html для просмотра в браузере). А с результатами, которые можно получить с использованием этого дифференциального уравнения, можно ознакомиться, проведя вычислительные эксперименты на математической квазимодели КШМ в программе Krivoship1, где используется это уравнение. Для этого надо в рамке <Метод получения уравнений> выбрать переключатель <уравнений Лагранжа 2-го рода> (скачать программу можно с моих сайтов в разделе Программы, где можно также скачать и архивы файлов krivo1 и krivo2).

Рис. 8. Моделирование работы КШМ по описанию, полученному с использованием силового подхода. Скриншот программы Krivoship1.

Вот только ничего интересного о системе с использованием этого уравнения узнать не получится, т.к. единственное, что это уравнение может дать, это скорости и углы поворота шатуна и кривошипа и перемещение поршня при свободных колебаниях, т.е. когда момент сопротивления равен нулю и на поршень не давят газы. А, чтобы посмотреть, как будут изменяться эти углы и скорости под нагрузкой, нам надо задать еще момент сопротивления и внешние силы, т.е. силы давления газов на поршень, которые будут изменяться по определенному алгоритму. Конкретно в программе Krivoship1 задан алгоритм работы двухтактного двигателя, где весь рабочий цикл совершается за один оборот кривошипа, а на рис. 8 Вы видите, что вследствие того, что работа момента сопротивления больше работы совершаемой поршнем, у нас скорость вращения кривошипа постепенно уменьшается и в конце-концов начинается его вращение в другую сторону.

В общем-то, чтобы определить скорости и углы поворота шатуна, кривошипа и перемещение поршня, как при свободных колебаниях, так и под нагрузкой, не обязательно решать аналитически уравнение (34) и можно его решить численными методами, что и делается в программе Krivoship1. Но вот для того, чтобы определить усилия, возникающие в элементах КШМ, необходимо обязательно сначала решить уравнение (34) аналитически, а потом составить для этой системы еще уравнения Лагранжа 1-го рода и уже, решив их, найти усилия, возникающие в элементах системы. Хотя и тут есть один вариант решения, который я применяю для описания явлений Природы при использовании силового или мощностного подходов. А конкретно, мы можем сразу и решать дифференциальные уравнения, полученные с использованием энергетическо-геометрического подхода Лагранжа, и находить усилия, возникающие в элементах системы, если соединим элементы системы упругими связями. И хотя при этом у нас формально должно получится еще в два раза больше уравнение (34), т.к. теперь у нас в системе будет и потенциальная энергия в этих соединениях, но теперь у нас получается, что не будет самих обобщенных координат, т.к. теперь все элементы соединены друг с другом не жестко.

Таким образом, у нас исчезло единственное достоинство энергетическо-геометрического подхода Лагранжа, а именно наличие минимального числа дифференциальных уравнений для описания систем. И теперь для описания КШМ надо будет использовать 5 координат, но это единственная возможность не только сразу решать дифференциальные уравнения и находить усилия в элементах системы. Более того, теперь мы можем найти даже резонансные частоты системы, хотя сделать это, решая дифференциальные уравнения аналитически, будет очень не просто и, к тому же, толку от этого будет очень мало, т.к. мы все равно не узнаем какие будут на этих частотах динамические нагрузки. А вот, если мы будем решать эту систему дифференциальных уравнений численными методами, то мы получим исчерпывающую информацию о динамических нагрузках возникающих не только при нормальных режимах работы систем, но и в режимах резонансов и биений.

И тут возникает вопрос. А зачем нам теперь надо для дифференциального описания нашей системы использовать манипуляции (32), если точно такое же описание мы можем получить, используя уравнения Эйлера (33). Ведь теперь нам надо проделывать манипуляции (32) пять раз для каждой из координат, по которым теперь описывается движение элементов системы, но сделать это на несколько порядков проще с использованием уравнения (33). Поэтому, я всегда применяю именно такой метод для дифференциального описания явлений Природы (или искусственно созданных систем), а для описания конкретно КШМ система дифференциальных уравнений, описывающих его поведение, будет выглядеть как (35), где: J1 = m1 * R^2 / 3 - момент инерции кривошипа относительно оси вращения, J2 = m2 * L^2 / 12 момент инерции шатуна относительно его оси вращения и L1 = L / 2 - половина длины шатуна L. Расчетная схема для этого описания приведена на рис. 9.    

Рис. 9. Расчетная схема кривошипно-шатунного механизма для описания по декартовым координатам.

J1*d2j1/dt2 = Fy21*R*cos(j1) - Fx21*R*sin(j1) - Mс - m1*g*R*cos(j1) / 2

m2*d2X2/dt2 = - Fx21 - Fx23

m2*d2Y2/dt2 = - Fy21 - Fy23 - m2*g

J2*d2j2/dt2 = (Fy21 - Fy23)*L1*cos(j2) - (Fx21 + Fx23)*L1*sin(j2) (35)

m3*d2X3/dt2 = Fx23 - Fg         если cos(j1) < 0                       то Fg = 0    

                                                   если cos(j1) > 0  и sin(j1) > 0 то Fg = Fmax

                                                   если cos(j1) > 0  и sin(j1) < 0 то Fg = 0.2*Fmax

При этом движение кривошипа опишем одним уравнением, как его вращением  вокруг оси Z, движение шатуна опишем тремя уравнениями: движением его центра масс по осям X и Y и вращением шатуна вокруг оси Z проходящей через его центр масс, а движение поршня опишем одним уравнением вдоль оси X. Здесь у меня Fg это сила давления газов в камере сгорания на поршень, которая при рабочем ходе будет Fmax, при сжатии рабочей смеси будет 0.2*Fmax, а при выпуске отработавших газов и при всасывании рабочей смеси Fg = 0. Условия изменения этих сил сформулированы из условия, что двигатель двухтактный, т.е. весь цикл в двигателе проходит за один оборот кривошипа. В этих уравнениях не хватает выражений для определения сил возникающих в упругих элементах, соединяющих элементы системы, которые надо вычислять по уравнениям (36). Как все это будет вычисляться при аналитическом решении этой системы я не знаю и никому этим заниматься не советую, но если очень хочется, то я бы все же порекомендовал делать это не на листочке бумаги, а перепоручить это решение какому ни будь математическому пакету символьных вычислений. А вот при численном решении этой системы уравнений (35) необходимо вычислить по уравнениям (36) значения сил перед тем, как обращаться к системе дифференциальных уравнений. Причем, если Вы будете решать систему дифференциальных уравнений методом Рунге-Кутта по 4-м коэффициентам, т.е. будете 4-е раза обращаться к этой системе дифференциальных уравнений, то и силы надо будет тоже вычислять 4-е раза.

X12 = R * cos j1                                           Y12 = R * sin j1

X21 = X2 - L1 * cos j2                                 Y21 = Y2 - L1 * sin j2

X23 = X2 + L1 * cos j2                                Y23 = Y2 + L1 * sin j2

Fx21 = (X21 - X12) * C12                             Fy21 = (Y21 - Y12) * C12

Fx23 = (X23 - X3) * C23                               Fy23 = (Y23 - Y3) * C23 (36)

Здесь C12, C23 - радиальная жесткость шарниров соединяющих шатун с кривошипом и шатун с поршнем соответственно, X12 ,Y12 – координаты центра шейки кривошипа контактирующей с шатуном, X21 ,Y21 - координаты центра головки шатуна контактирующей с шейкой кривошипа, X23,Y23- координаты центра головки шатуна контактирующей с поршневым пальцем и X3,Y3- координаты центра поршневого пальца (Y3=0), которые определяются согласно расчетной схеме на рис. 10. При этом принято, что деформируются элементы головок шатуна, а шейка кривошипа и палец поршня приняты абсолютно жесткими, но при необходимости возможны и другие варианты расчета.

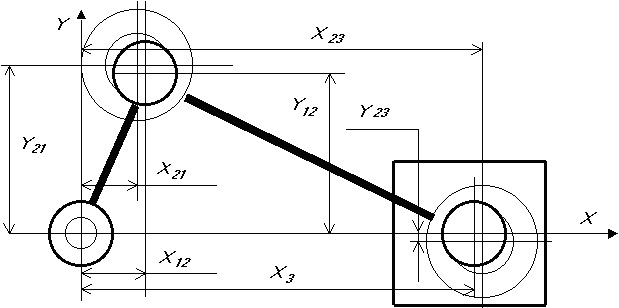
Рис. 10. Схема для определения сил в местах контакта элементов кривошипно-шатунного механизма.

При этом в любой системе всегда присутствует трение. Причем видов трения очень и очень много, а природа сил трения пока не известна, но с помощью различных аппроксимаций мы можем чисто количественно описать многие эти процессы вполне удовлетворительно [5]. Например, хорошо аппроксимируются сухое трение и жидкостное (линейное и квадратичное), но, если нет необходимости учитывать конкретный вид трения, то проще всего учесть при дифференциальном описании линейное жидкостное трение. Это позволяет не только более качественно описать конкретные системы, но и позволяет сгладить при резких скачках нагрузки сильные колебания элементов системы на упругих элементах соединяющих части системы. При учете жидкостного трения в местах контактов элементов систем в уравнениях (36) добавятся скорости концов шатуна и кривошипа (скорость поршня известна) и возникающие в этих двух шарнирах силы жидкостного трения при заданных значениях коэффициентов жидкостного трения Kj12 и Kj23 (37), где w1= dj1/dt – угловая скорость вращения кривошипа, а w2= dj2/dt – угловая скорость вращения шатуна относительно его центра масс. Обычно, если это не вытекает из задач исследования, я принимаю значения этих коэффициентов для всех соединений одинаковыми (точно также, как и значения податливости (величина обратная жесткости) всех деталей в местах контакта).

VX12 = -  w1 * R * sin j1                              VY12 = w1 * R * cos j1

VX21 = VX2 + w2 * L1 * sin j2                    VY21 = VY2 - w2 * L1 * cos j2

VX23 = VX2 - w2 * L1 * sin j2                     VY23 = VY2 + w2 * L1 * cos j2

Fx21j = (VX21 -VX12) * Kj12                        Fy21j = (VY21 - VY12) * Kj12

Fx23j = (VX23 -VX3) * Kj23                          Fy23j = (VY23 - VY3) * Kj23            

Fx21 = Fx21 + Fx21j                                        Fy21 = Fy21 + Fy21j

Fx23 = Fx23 + Fx23j                                        Fy23 = Fy23 + Fy23j (37)

Таким образом, мы видим, что при силовом подходе дифференциального описания явлений Природы и искусственных систем весь процесс получения дифференциальных уравнений сводится к простейшему набору одних и тех же операций при описании движения по каждой из декартовых координат и по углам поворота относительно этих осей (тоже самое относится и к описанию в приращениях). И при этом мы получаем именно математическую модель явления или системы, а не квазимодель (34) которая получается при использовании уравнений Лагранжа 2-го рода для описании систем по минимальному количеству обобщенных координат. При этом необходимо вспомнить и ещё одно основное отличие модели от имитатора, которое заключается в том, что модель способна к совершенствованию, т.е. к усложнению или уточнению без переделки всей модели, а новый имитатор (в нашем случае это квазимодель, полученная с использованием манипуляций Лагранжа), можно создать только пройдя весь путь по созданию описания заново. Например, в математической модели можно изменить конструкцию кривошипа и это затронет только уравнения связанные с описанием его движения совершенно не касаясь уравнений, описывающих движение поршня и шатуна. А для получения описания с помощью методов предложенных Лагранжем необходимо при любом конструктивном изменении в системе провести почти все математические выкладки по получению уравнений, описывающих поведение системы, заново, что является явным признаком имитатора.

При этом, ради справедливости стоит заметить, что во времена Лагранжа его энергетическо-геометрический подход, т.е. не его основное уравнение динамики, которое, к тому же было и ошибочным, а его чисто математический прием, позволявший сократить число дифференциальных уравнений, описывающих поведение систем, до минимума, т.е. до минимального количества обобщенных координат, имел практический смысл. Ведь силовой подход Эйлера для описания явлений Природы давал математическое описание только в декартовой системе координат и для сложных систем получалось очень много уравнений, решить которые совместно было не всегда возможно и надо было, используя другие математические приемы, потом сокращать число этих уравнений, а энергетическо-геометрический подход Лагранжа позволял получить сразу минимально возможное число дифференциальных уравнений. Но все это имеет значение только при аналитическом решении этой системы дифференциальных уравнений, а с появлением компьютеров, когда мы можем применять и численные методы их решения, это уже не имеет никакого значения. И я, например, в своей программе Solsys элементарно решаю численными методами систему из 33 дифференциальных уравнений второго порядка, которые описывают поведение планет Солнечной системы.

Как я уже писал выше, для получения дифференциального описания можно использовать не только силовой подход, но и мощностной, т.к. при этом тоже используется баланс для мгновенных мощностей, как и при силовом подходе для мгновенных сил. При этом мощностной подход позволяет нам записывать уравнения мощностного баланса и в функции энергии деленной на время и в функции силы умноженной на скорость. Выше я использовал уравнение мощностного баланса, которое получается из энергетического баланса путем деления энергий на время (только энергии я брал не в начале и конце разгона, как при энергетическом подходе, а средние на интервале Δt), но можно было и силы умножить на скорость. Вот только в данном частном случае (разгона ракеты) у нас мощностной подход, как это часто бывает вырождается в силовой, но так бывает не всегда и при рассмотрении вопроса качения колеса я покажу, что в этом случае применим только мощностной подход, а силовой подход не возможен. При описании топливной ракеты в приращениях мы использовали мощностной подход в записи (38), но его можно было выполнить и в записи (39). Вот только в последнем случае у нас обе части баланса сокращались на Vsr и мы приходим к силовому балансу (13-3).

(m1-mg1*Δt /2)*Vsr*ΔV/Δt = P + mg1*Vsr^2/2 - mg1*Vg^2/2        (38)        мощностной

Vsr*(m1-mg1*Δt /2)*ΔV/Δt = Vsr*mg1*Vgo                                     (39)        мощностной

(m1-mg1*Δt /2)*ΔV/Δt = mg1*Vgo                                                     (13-3)     силовой

Но мощность можно выразить и как произведение крутящего момента на угловую скорость и вот именно эта особенность и позволяет с использованием мощностного подхода правильно описать процессы качения колеса. Сразу замечу, что даже более-менее корректно описать движение колеса на порядок сложнее, чем описать работу атомного реактора или движение ракеты, поэтому я дам очень упрощенное описание этого процесса. А, кого интересуют подробности, я отсылаю к своей диссертации [5]. При этом уравнение мощностей нам здесь понадобится два раза. Сначала мы с его использованием найдем момент сопротивления качению одного колеса, а потом определим силу, действующую на ось колеса в горизонтальной плоскости при наличии внешних горизонтальных сил. Начнем с момента сопротивления качению одного колеса. В учебниках его определяют как произведение мифической силы сопротивления качению колеса на его динамический радиус, но на самом деле никакой силы сопротивления качению не существует. Вот только с использованием силового подхода авторы учебников не смогли придумать ничего другого, как мифическую силу сопротивления качению колеса так же, как раньше изобретали живые и мертвые силы, о чем я писал выше, а также силу пищеварения, силу любви, силу разума и т.д. Давайте рассмотрим на рис. 11 силы и моменты, которые будут на самом деле действовать при равномерном качении ведущего колеса полноприводных трактора или автомобиля при их равномерном движении по несминаемому основанию.

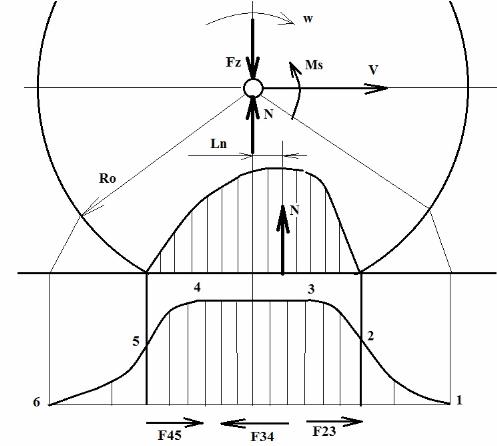
Рис. 11. Схема к расчету момента сопротивления качению ведущего колеса при отсутствии внешних горизонтальных сил и эпюры нормальных напряжений в пятне контакта (вверху) и окружного сжатия шины (внизу).

Во-первых, посмотрим на эпюру нормальных напряжений в пятне контакта. Здесь мы видим, что из-за гистерезисных потерь внутри материала шины центр тяжести эпюры смещен в переднюю часть и, следовательно, сила давления опорного основания N будет смещена на величину Ln, что даст момент сопротивления качению N*Ln. А теперь давайте посмотрим на эпюру окружного сжатия шины, которое возникает вследствие того, что длина деформированной окружности стала меньше и теперь элементы шины, расположенные по ее периметру, уменьшили свою длину на участке от точки 1 до точки 6 и длина окружности деформированной шины уже не равна 2*pi*Ro. При этом от точки 1 до точки 3 идет окружное сжатие протектора, а от точки 4 до точки 6 идет восстановление нормального расстояния между соседними элементами протектора. Это приводит к тому, что в пятне контакта от точки 2 до точки 3 возникают касательные напряжения из-за того, что эти элементы протектора притягиваются к средней части протектора 3-4, и возникает в пятне контакта касательная сила F23. А на участке 4-5 у нас элементы протектора наоборот отталкиваются от средней части протектора 3-4 и тоже возникает в пятне контакта касательная сила F45.

При этом средняя часть протектора будет практически неподвижна относительно опорного основания, хотя, незначительное смещение, необходимое для возникновения силы трения покоя, все же будет возникать, и эта сила трения покоя F34 будет равна сумме сил F23 и F45 и направлена будет в противоположную от них сторону, т.е. для пятна контакта это будут внутренние силы, которые не будут создавать горизонтальной силы сопротивления качению колеса. Но ведь работу то эти силы в пятне контакта будут совершать и на это должна расходоваться часть энергии подводящейся к колесу через крутящий момент. Расписывать подробно, как я, разбив пятно контакта на множество маленьких участков, находил смещение относительно опорного основания каждого участка, а потом по нормальным напряжениям находил касательные напряжения на этих участках и силу трения, а потом по скорости проскальзывания этих участков относительно опорного основания находил мощность рассеянную в пятне контакта, я не буду. Скажу только, что при желании эту мощность P25 определить можно и, следовательно, зная угловую скорость вращения колеса w, можно найти момент сопротивления при качении колеса, который, исходя из мощностного подхода, определится как

Ms= N*Ln + P25/w                                   (41)

А теперь давайте рассмотрим ошибку, которая возникает при использовании силового подхода, при рассмотрении вопроса качения колеса при действии на него еще и внешних горизонтальных сил. Такими силами будут сила инерции Fj трактора или автомобиля при их ускоренном движении, силы сопротивления Fs от ведомых колес или колес прицепа, которые, чтобы они крутились, надо или толкать или тащить, и касательная сила Fk, возникающая в пятне контакта. При этом силы Fj и Fs передадутся колесу через ось колеса и в сумме дадут силу Fe, которая будет действовать уже непосредственно на массу колеса в горизонтальной плоскости. Тогда движение колеса в горизонтальной плоскости опишется уравнением

m*dV/dt=Fk-Fe                                          (42)

Но сила Fk теперь уже не будет равна нулю, как это у нас было при равномерном качение одного колеса, т.к. теперь у нас в пятне контакта на участке 3-4 элементы протектора тоже будут или частично или полностью смещаться в ту же сторону, что и элементы протектора на участках 2-3 и 4-5. Подробно расписывать как в этом случае по смещениям элементов протектора вычислять касательную силу Fk и мощность P25, которая будет немного отличаться от подсчитанной при свободном качении колеса, я опять не буду, а только констатирую, что при желании определить их можно. Естественно, в учебниках о том, как определять силу Fk, ничего не написано и дается только формула для определения максимально возможного значения этой силы, как произведение веса трактора или автомобиля, приходящихся на эту ось, на коэффициент сцепления шины с конкретным опорным основанием.

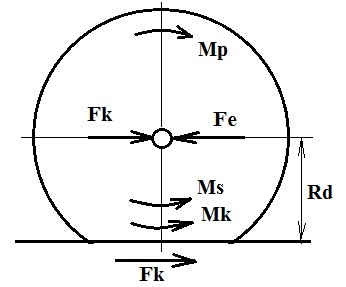
Рис.12. Взаимодействие ведущего колеса автомобиля или трактора с несминаемым опорным основанием при наличии внешних горизонтальных сил.

Но допустим, что авторы учебников, используя мои формулы, определили эту силу. Что они предлагают дальше для описания движения колеса. А они предлагают определять момент сопротивления, приложенный к колесу от воздействия касательной силы Fk, при переносе ее по правилам теоретической механики к цетру масс колеса, т.е. к полуоси, как Mk = Fk*Rd, где Rd это динамический радиус качения колеса (расстояние от опорной поверхности до оси вращения колеса при его движении). И в таком случае у нас вращение колеса опишется дифференциальным уравнением

                       Jk*dw/dt = Mp - Mk - Ms                                         ( 43)

Здесь у нас Jk это момент инерции колеса, а Mp это момент приложенный к колесу со стороны полуоси. Но давайте внимательно приглядимся к мощности, которую сила Fk передает колесу для его движения в горизонтальной плоскости. Эта мощность будет Fk*V и, следовательно, эта же мощность должна затрачиваться колесом при его вращении как Mk*w, отсюда находим, что Mk= Fk*V / w = Fk*Rk. Здесь Rk это кинематический радиус, который определяется как Ro*(1-ξ), где ξ это максимальное окружное сжатие шины в пятне контакта. Таким образом, т.к. Rk совершенно не равно Rd, то и момент сопротивления от касательной силы Mk = Fk*Rd, определяемый в учебниках исходя из силового подхода, тоже подсчитывается не правильно. Да, колесо выступает в данном случае в роли сложного редуктора трансформирующего угловую скорость в поступательную и силу в крутящий момент, а поэтому правильно описать эти процессы можно только с использованием мощностного подхода. А кому интересно ознакомится с дифференциальным описанием движения всего автомобиля или колесного трактора, могут посмотреть это здесь [5].

                  методы решения уравнений математического описания динамических систем

Надеюсь, что приведенный мною теоретический материал и конкретные примеры позволят теперь любому желающему корректно и без напряжения описать любые явления Природы и искусственно созданные системы с использованием различных подходов, как в конечном описании, так и в текущем (дифференциальном или в приращениях). И теперь осталось только изложить материал, связанный с решением систем уравнений, описывающих наши системы на языке математики. Что касается различных методов аналитического решения систем дифференциальных уравнений, то останавливаться на этом я почти не буду, т.к. эти вопросы широко освящены в литературе. А вот на численном решении текущего описания систем, как в дифференциальной форме, так и в приращениях я остановлюсь подробно. Исторически сложилось так, что численное решение сложных задач стало возможно только после изобретения компьютеров, а до этого были только разработаны методы численного решения, но решения практически всегда осуществляли аналитическое или геометрическое (если не считать некоторых простейших решений, которые сделал Архимед). Но и сейчас, когда повсеместно используются компьютеры, во всех учебниках рассматриваются только аналитические методы решения задач. Причем студентов упорно убеждают, что аналитическое решение является точным, а численное приближенным, хотя на самом деле все наоборот.

Да, существует масса математических задач (повторяю еще раз именно математических), которые решаются аналитически точно, но в Природе таких задач практически нет и получается, что математикам нечего делать в физике. Но им давно уже нечего делать и в математике, поэтому эти математико-физики, т.е. математики, перебравшиеся в физику, стараются как то теоретически обосновать свою нужность в физике. Например, Ландау, чтобы демонстрировать на полных основаниях свои математические познания в физике, во введение к тому Механики 1940 года издания делит всю физику на экспериментальную, теоретическую и математическую. Естественно, он будет заниматься теоретической физикой, а в ней очень важную роль играют приближенные вычисления, которыми он только и занимается, т.е. он будет решать приблизительные задачи с приблизительным решением. Конкретно он пишет

«Таким образом приближения играют очень важную роль в общих физических законах. Не менее велика, однако, их роль и при выводе из общих теорий конкретных физических законов. Слишком точные вычисления с учетом несуществующих факторов не только бесплодны и излишне усложняют результаты расчета, но могут даже привести к тому, что существующие в данном явление закономерности вообще выпадут из рассмотрения.»

Здесь, правда, надо заметить, что в издание 1958 года все эти его графоманские рассуждения о трех различных физиках, которые были во введении, додумались все-таки убрать (вместе со всем введением), но вот в последнем издании 2004 года [3] я вдруг обнаружил их опять (правда в приложении и назвали это введение теперь предисловием к первому изданию, но все же вытащили на белый свет, а значит, что это опять кому-то надо).

Но я еще раз повторяю, что в Природе таких задач в дифференциальном описании, которые бы решались аналитически точно, практически нет и даже уравнение математического маятника является нелинейным и аналитически не решается. Поэтому математико-физики, чтобы продемонстрировать свою потребность в физике, сначала реальные задачи переводят в условно решаемые, т.е. приблизительные, а потом их решают чаще всего опять таки приблизительными методами. Причем, говоря о приблизительных методах, я не имею в виду, например, итерационные методы решения дифференциальных уравнений, а говорю о различных манипуляциях, которые позволяют сделать не решаемые аналитически дифференциальные уравнения решаемыми. И впервые о фокусах, которые проделываются при аналитическом решении дифференциальных уравнений, я упомянул еще в своей диссертации, где привел пример из учебника по динамике трактора и автомобиля, где авторы в дифференциальном уравнении, которое даже имело аналитическое решение, для простоты его решения просто зачеркнули один член в уравнении и решали оставшуюся часть.

А, что касается перевода задач в условно решаемые, то здесь сначала отбрасывают массу мелких эффектов, которые затрудняют решение, т.к. считается, что они существенно не повлияют на ответ. Потом, если задача получается не решаемой принципиально, например, получили не линейные дифференциальные уравнения, то ее переводят в решаемую или прямой заменой нелинейных эффектов линейными, например, сухого трения жидкостным или нелинейной жесткости линейной или производят замену нелинейной части уравнения ее приблизительным значением, производя ее разложение в ряд с использованием степенных функций и с отбрасыванием членов высоких порядков и т.д. Так в примере с математическим маятником заменяют sin(φ) на φ, хотя это и приводит к большой ошибке при φ=1,57 рад, т.к. синус при этом получается равен единице. Вот фрагмент моего файла nelinsys22.mws http://modsys/narod.ru/Arhiv/nelinsys22mws.zip  для математического пакета Maple, где я рассматриваю аналитическое и численное решение дифференциального уравнения описывающего (моделирующего) движение математического маятника. Кстати, эти же вычисления и для маятника и для кривошипно-шатунного механизма для пакета Maple я нашел и на сайте Экспоненты, поэтому можете скачать похожий файл и оттуда http://exponenta.ru/educat/systemat/chudinov/mech.asp).

> restart;

> # запишем уравнение колебаний маятника приняв k[l]:=g/l:

> de1:=diff(x(t),t$2)=-k[l]*sin(x(t));

> # как ни странно, но это уравнение не имеет аналитического решения потому что оно не линейное и мы можем в этом убедиться, предложив его решить программе Maple (естественно, выданный ей результат, нас не устраивает)

> d1:=dsolve({de1,x(0)=3.14,D(x)(0)=0},x(t));

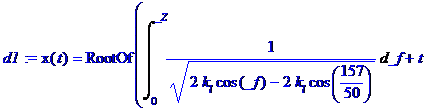
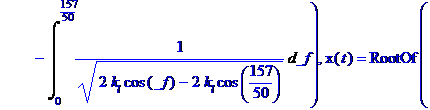
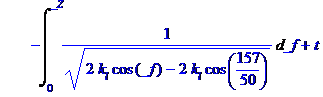
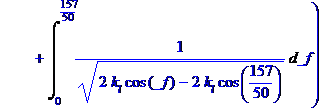
> # но если вместо sin(x(t)) написать просто x(t), что при малых x будет примерно соответствовать действительности, то такое уравнение будет линейным и его можно решить аналитически

> de2:=diff(x(t),t$2)=-k[l]*x(t);

> d2:=dsolve({de2,x(0)=1.57,D(x)(0)=0},x(t));

> g:=9.81:l:=1:k[l]:=g/l:

> evalf(d2);

> # теперь по этому уравнению построим график колебаний маятника

> plot(1.57*cos(3.1321*t),t=0..10);

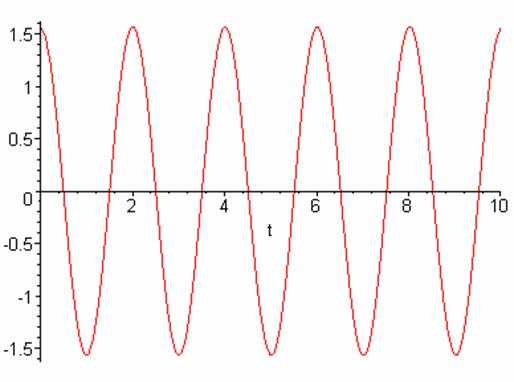
> # а теперь решим численными методами наше исходное уравнение и сравним результат с данными полученными аналитическим методом при подгонке нашего уравнения под линейное

> with(DEtools):

> DEplot(de1,[x(t)],0..10,[[x(0)=1.57,D(x)(0)=0]],stepsize=.01,linecolor=black,arrows=none,thickness=2);

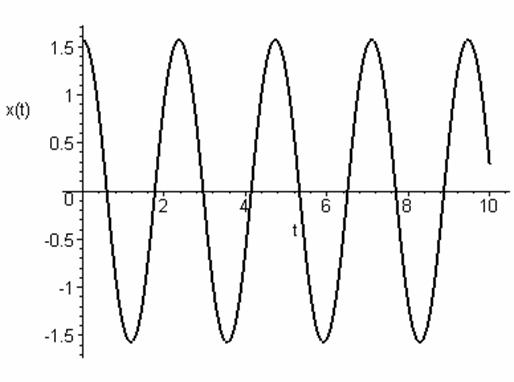
Как видим, при амплитуде колебаний pi/2 у нас получается погрешность в периоде колебаний почти 20%, что является отличным результатом для экономических моделей, но совершенно не допустимо для механических моделей. А, к чему приводит разложение в ряд, я показал на конкретном примере в своей статье [10], который повторю и здесь. Так на стр.47 [4] Ландау пишет

«Для осуществления этого перехода разложим L в ряд по степеням v/c. Тогда, опуская члены высших порядков, получаем: L= -a*c*sqrt(1-v^2/c^2) ≈ -a*c + a*v^2/(2*c).»

Возьмем для примера a=1, v=290000 км/с, c=300000 км/с и получаем

-a*c*sqrt(1-v^2/c^2) = -76,81

-a*c + a*v^2/(2*c) = -159,83.

Т.е. здесь это приводит к явной ошибке в сотни процентов, но, как я уже писал, Ландау во введении к нулевому изданию своей Механики [1] не только постарался подвести какой то базис под приблизительное решение приблизительных задач, но и пытался доказать, что настоящий ученый только так и должен поступать. А при таких приблизительных методах аналитического решения задач можно получить самые разнообразные ответы, т.е. в зависимости от того, какой ответ нам нужен, мы можем выбрать тот или иной метод приблизительного решения. Показательным в этом плане является пример касающийся уже непосредственно рассматриваемого мною в работе [14] вопроса, о смещении параметров орбит планет. Вот фабула приблизительного аналитического решения по определению смещения перигелия Меркурия выполненного в работе [27].

«Как видно из рис. 11.1, при малых βp < 0.3 период траектории φt приближается к единице асимптотически, так что оценить значение φt при таких малых βp, которые присущи Меркурию не возможно. Численное интегрирование уравнений (4.80). (4.82) при таких параметрах дает погрешность, намного превышающую ожидаемое смещение перигелия δφt, в связи с этим рассмотрим приближенное решение уравнения траектории при малых βp. Запишем ……..

Так как мы рассматриваем Солнце, то для него Rg<<1, и при малых βt величина A<<1. Поэтому, экспоненту можно разложить в ряд Тейлора….

Разлагая знаменатели слагаемых в правой части и ограничиваясь членами второго порядка, получаем …..

В (11.15) мы ограничивались слагаемыми с показателями степени R меньше 6. Подставляя (11.15) в (4.80), с учетом слагаемых не выше R^3 имеем …..

При β0→0 коэффициенты имеют следующий порядок: F≈1; D≈1; Rg≈1/c1^2; E≈1/c1^4; M≈1/c1^2; N≈h/c1^2; DE≈1/c1^4. Поэтому, пренебрегая слагаемыми с y^3, выражение (11.20) можем проинтегрировать при граничном условии φ(Rp)=0, т.е. угол отсчитывается от перицентрия: …….

Так как гравитационный радиус планет Rg<<Rp, то влияние слагаемых во второй скобке не существенно, поэтому окончательно при βp<<1 вращение перицентрия получаем в виде

Δφt = -2*π*a1^2*βp^2                              (11.31)

Как видим, смещение перицентрия происходит в обратную сторону, т.е. за период частица по орбите проходит угловое расстояние, меньше 2*π. Это противоречит всем полученным нами решениям, в том числе и представленным на рис. 11.1. По абсолютной величине смещение (11.31) превышает значения, рассчитанные численно: (приводится таблица).

Таким образом, полученное приближенное аналитическое решение (11.31) является ошибочным.»

Таким образом, у автора этого решения не просто получилась ошибкам в сотню процентов, как мы это видели с примером решения у Ландау, но ответ получился принципиально другим, т.е. получилось отрицательное смещение перигелия. Здесь же надо заметить, что, когда автор писал о больших ошибках численного интегрирования при решении уравнений (4.80) и (4.82), то речь там шла о решении промежуточного решения полученного им же аналитически, поэтому, ошибка-то у него быстрее всего была при аналитическом решении, т.к. при численном интегрировании может быть только небольшая погрешность решения. Причем, что интересно, и при аналитическом выводе им уравнения (4.80) мы встречаем такие же выражения

«Это нелинейное дифференциальное уравнение второго порядка. Рассмотрим его решение. С этой целью перейдем к новым переменным …..»

«Таким образом, мы свели (4.68) к нелинейному дифференциальному уравнению первого порядка. Перейдем к новым переменным ….., которые сводят (4.72) к линейному дифференциальному уравнению первого порядка. ….»

Т.е. здесь мы видим конкретный пример приведения исходных нелинейных дифференциальных уравнений к линейным. А при решении дифференциальных уравнений численными методами нам все равно какие у нас исходные уравнения (линейные или нелинейные) и сколько и каких эффектов они учитывают. А, как показала моя практика, при их решении на современных компьютерах, например, методом Рунге-Кутта, при правильно подобранных параметрах, ошибка решения обычно не превышает тысячных долей процента. Таким образом, при решении реальных физических задач, а не учебных, надо говорить о том, что численное решение дает почти точный результат, а аналитическое приблизительный. И даже, если разные авторы получили одинаковый результат при приблизительном аналитическом решении приблизительных уравнений, это ни в коей мере не является доказательством того, что будет наблюдаться именно этот эффект. А то вот автор, вышеприведенных длинных цитат, хоть и получил результат с другим знаком, но пытается показать, что его решение не совсем ошибочное и возможно, что это решение Гербера и Эйнштейна ошибочное, а заодно и Сухорукова [28], формулу которого я тоже проверял в своей работе [14]. Кстати, у меня там по формуле Сухорукова получилось при численном решении 8,7294 угл.сек за сто лет, а он согласно своему аналитическому решению по своей формуле (81*) получил 13,99 угл.сек.

Да я бы не удивился, если бы у Сухорукова получился и совсем другой результат, т.к. все эти аналитические методы решения реальных задач являются приблизительными методами решения приблизительных задач и доверять полученным аналитическим решениям без их проверки численными методами никак нельзя. А в заключении, чтобы Вам стала более понятна вся абсурдность приблизительных аналитических методов решения приблизительных задач и выводов, которые из таких решений делаются, я позволю себе привести еще одну длинную цитату из работы [27]

«Смещение перигелия (11.4), полученное П. Гербером и подтвержденное А. Эйнштейном после подстановки ε, Т и а, согласно (5.14), (5.36) и (5.15), принимает вид

Δφt = 6*π*a1^2*βp^2                              (11.34)

Как видим, полученное нами выражение (11.31) дает в 3 раза меньший по абсолютной величине результат. Г.И. Сухоруков и др. [28] получили тоже в 3 раза меньшее смещение перигелия Меркурия по сравнению с (11.34). Численное значение (11.34) для Меркурия составляет Δφt = 5*10^-7, которое, хотя и в 200 раз больше полученного нами значения 2.7*10^-9, но все же представляет достаточно малую величину. В работе А. Эйнштейна [23] задача двух тел сводится к интегралу (автор приводит  выражение 11.35*), который идентичен полученному нами интегралу (11.20). Последний мы решали, ограничиваясь слагаемыми с y^2. А. Эйнштейн интегрировал (11.35) также приближенно, но другим методом. Этим и объясняется отличие результата (11.34) от (11.31). И оба они являются неверными приближенными решениями точного уравнения траектории (4.80)-(4.82).

        В заключение подведем некоторые итоги.

1. Действительная величина прецессии перигелиев планет в настоящее время остается неопределенной.

2. Зависимость силы взаимодействия двух тел от скорости приводит к прецессии перицентрия. При очень малых скоростях смещение перицентрия за оборот определяется выражением (11.33), и для Меркурия оно составляет 2.7*10^-9 радиана или 0.23’’  в столетие. Этот эффект представляет такую малую величину, что она никогда не сможет быть подтверждена наблюдениями.

3. Величина смещения перигелия Меркурия, определенная У. Леверье на основе закона тяготения Ньютона, подлежит сомнению и для его нахождения должна быть решена проблема многих тел.»

А теперь давайте уже мы подведем итоги по итогам, которые сделал математико-физик Смульский. Здесь мы с одной стороны видим явное утверждение о том, что все аналитические методы решения являются приближенными и могут давать совершенно разные результаты, а с другой стороны мы видим слепую веру в безупречность полученного им аналитического решения (4.80*). И даже расчетные данные Гербера и Эйнштейна, хоть они и отличаются от полученных им данных, он ставит выше наблюдаемых данных. Более того, Смульский утверждает, что раз данные наблюдений не подтверждают его теорию, то ошибочными являются именно данные наблюдений.

Правда, он оставляет нам маленькую возможность возразить ему, если мы решим проблему многих тел и подтвердим величину смещения перигелия Меркурия определенную Леверье. Ну, так я как раз и решил эту проблему почти точными методами численного решения дифференциальных уравнений, и доказал справедливость данных Леверье [13]. Так что все эти выводы математико-физика Смульского о справедливости его теории ошибочны. А вот его вывод о том, что «Этот эффект представляет такую малую величину, что она никогда не сможет быть подтверждена наблюдениями» уже явно не является выводом о точности аналитических решений и попахивает позитивизмом и явным утверждением о том, что мир не познаваем. И тут Смульский оправдывает философские взгляды других математико-физиков, которые отрицают познаваемость микромира и утверждают, что мы можем только статистическими распределениями описать в современной квантовой механике видимые нами эффекты от процессов, протекающих в микромире. А делают они так не потому что имеют какие-то философские взгляды на вопросы микромира, а потому, что они, во-первых, не могут грамотно описать эти процессы, а, во-вторых, они принципиально не могут решить эту задачу аналитически, т.к. уже в атоме гелия мы имеем ядро и два электрона, а это уже задача трех тел.

Таким образом, вся научная философия математико-физиков сводится не к изучению внутренних пружин заставляющих протекать процессы так или иначе, а к изобретению различных математических выражений, которые бы удовлетворительно описывали наблюдаемые нами эффекты. При этом закрываются глаза на любые несуразности и ошибки, если полученная формула позволяет это сделать, например, как мы это видели у Планка [9] при выводе им своей формулы. Или возьмем ОТО Эйнштейна, где считается, что скорость распространения гравитации равна скорости света, но все решения с применением этой теории, которые приводятся в учебниках, получены аналитическим путем, а сделать это не возможно при учете скорости гравитации для расчета запаздывания по координатам. Таким образом, и в ОТО, также как и у Гербера, фактически принята скорость гравитации равная бесконечности. Да у них и уравнение для расчета аномального смещения перигелия Меркурия получилось одно и то же. При чем, что интересно, свои уравнения гравитационного поля Эйнштейн получил уже после того, как опубликовал эту формулу [23], т.е. получается, что он просто передрал эту формулу у Гербера, а потом подгонял свои уравнения поля под нее. Хотя, здесь не все так однозначно,  т.к. само решение общековариантного тензорного уравнения Эйнштейн украл у математика Гильберта, а тот, уж точно, ничего не подгонял под заданный ответ.

Вообще то примерно то же самое, т.е. подгонку своего решения задачи под заданный ответ (пусть даже и несознательно) делали все математико-физики и в то время делают и сейчас, т.к. они пытались и пытаются объяснить своими физическими теориями, например, именно аномальное смещение перигелия Меркурия, а не физическое явление гравитации. И хотя, нужный практический результат давала и просто поправка Холла к закону тяготения, но эти якобы ученые пытались получить нужный результат именно путем видоизменения закона тяготения исходя из каких-то теоретических предпосылок. А теории должны не заранее подгоняться под нужный результат, а создаваться исходя из существующих представлений об окружающем мире, а потом уже проверяться по получающимся результатам. Вообще-то за такие вещи, когда теория подгоняется под нужный результат, надо не Нобелевские премии давать, как, например, Планку и Эйнштейну или Тейлору и Халсу, а наказывать. Вопрос только в том, кто и как будет наказывать. При этом я не призываю казнить таких мошенников, как раньше казнили еретиков, а по подсчетам Вольтера таковых набралось 9 718 800 человек, но что-то надо делать, т.к. наука за последние 100 лет деградировала и многие достижения техники сделаны инженерами не благодаря таким теориям, как квантовая механика или ОТО, а вопреки им.

В общем, мне кажется, что процесс оболванивания в науке достиг своего апогея. И, если при работе над своей статьёй [10], я еще удивлялся, как все эти математико-физики не видят явных ляпов в применении принципа наименьшего действия у Ландау и Фейнмана, то сейчас я уже не знаю чему удивляться. И во многом этому оболваниванию способствует то, что и сейчас продолжают упорно учить студентов только аналитическим методам решения задач, а, т.к. реальные задачи не решаются аналитически, то выдумываются любые самые фантастические теории, где критерием их истинности является только то, что с использованием этих теорий решение задач можно получить аналитически. Т.е. во главу угла здесь ставится не физическая сущность рассматриваемых явлений Природы, а только требования математики к этим теориям. А, чтобы повернуть процесс развития науки в правильное русло, надо больше учить студентов именно численным методам решения задач, а не аналитическим, т.к. сложность решаемых сегодня задач возросла настолько, что аналитически они уже не решаются.

А вот, если мы опишем явления Природы в приращениях и будем потом по этому описанию решать эту задачу численным методом, то никаких проблем у нас не возникает. Точно также не будет никаких проблем ни с задачей трех тел, ни с нелинейностью дифференциальных уравнений, если мы будем решать систему дифференциальных уравнений, описывающих явление Природы или искусственную систему численными методами. При этом  простейшим методом численного решения дифференциальных уравнений является метод Эйлера, согласно которому по заданным в данный момент времени T1 координатам тел и их скоростям находятся силы, действующие на эти тела, а потом, согласно 2-у закону Ньютона в интерпретации Эйлера, т.е. уже в современной трактовке, находятся ускорения масс при действии на них, полученных сил. Затем, по найденным ускорениям, уточняются скорости тел и из предположения, что за очень маленький промежуток времени P0 они изменяться незначительно, делается расчет новых скоростей и новых координат тел в новый момент времени T1+P0 и т.д.

Но метод Эйлера очень не точен при большой кривизне траектории движения и особенно, если мы имеем знакопеременную функцию, поэтому накапливается большая  ошибка при увеличении времени решения задачи. Этих недостатков практически лишен метод Рунге-Кутта по 4-м коэффициентам, где у нас 4-е раза как бы прощупывается кривизна траектории для разных моментов времени, а потом делается окончательный расчет новых координат и скоростей для следующего момента времени T1+P0 с учетом полученных 4-х промежуточных значений координат и скоростей, рассчитанных для моментов времени T1, T1+P0/2 (два раза) и T1+P0. А при описании в приращениях у нас, как и в методе Эйлера, на одном шаге решения P0 (шаге приращения) делается только одно вычисление новых параметров системы, но точность решения получается гораздо выше. Наглядно точность этих двух методов отражает рисунок 13, где приведена зависимость высоты подъема камня в функции времени h(t). Но, допустим у нас нет этого аналитического решения, а есть только дифференциальное уравнение dh/dt=f(h,t) и нам надо его решить методом Эйлера, чтобы получить график зависимости h(t). В момент времени T1 скорость подъема dh/dt будет равна тангенсу угла наклона кривой h(t), т.е. тангенсу угла Q1e. Поэтому за шаг времени P0 у нас камень должен подняться на высоту h1e. На следующем шаге решения в момент времени T1+P0 касательная к функции h(t) будет проходить под углом Q2e, поэтому из этой точки проводим отрезок прямой под этим углом до момента времени T1+2P0 и получаем высоту h2e и т.д.

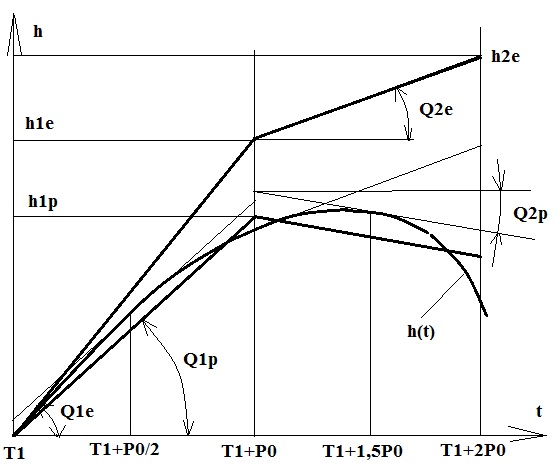
Рис. 13. Сравнительная схема численного решения в приращениях и методом Эйлера.

А при описании в приращениях у нас находится среднее приращение скорости на шаге решения, т.е. можно сказать, что мы находим производную в точке T1+P0/2, но при условии, что кривизна поверхности на этом шаге не изменяется, и потом мы вычисляем и среднюю скорость, что более точно отражает производную dh/dt на этом шаге решения. А далее мы точно также из точки T1 проводим прямую, но под углом Q1p и находим высоту в конце этого шага решения h1p. А потом уже из этой точки на следующем шаге решения проводим прямую под углом Q2p и т.д. Как мы уже видели выше, при решении задачи разгона топливной ракеты в приращениях у нас при шаге решения Δt= P0=0,001 секунды решение в приращениях дает очень хорошую точность. А сейчас давайте сравним ее с точностью численного решения дифференциального уравнения описывающего разгон топливной ракеты методами Эйлера и Рунге-Кутта с этим же шагом, т.е. тоже определим скорость ракеты через 170 секунд.   

V=379,423 996 977 176 - аналитическое решение

V=379,423 996 968 305 - решение в приращениях с P0=0,001

V=379,423 996 977 281 - решение в приращениях с P0=0,00025

V=379,423 996 978 800 - метод Рунге-Кутта с P0=0,001

V=379,421 163 663 565 - метод Эйлера с P0=0,001

Как видим, метод Эйлера действительно дает большую погрешность даже при незначительной кривизне функции скорости и таком маленьком шаге решения, а метод Рунге-Кутта дает отличный результат, т.к. точность решения даже на одну значащую цифру лучше, чем при решении в приращениях. Но при одинаковом времени решения, т.е., когда шаг решения в приращениях в 4 раза меньше, чем при решении методом Рунге-Кутта, точность решения в приращениях может быть даже выше. Но все это было в том случае, когда функция скорости не меняла знака, поэтому давайте посмотрим, как эти методы покажут себя при знакопеременной функции. Пусть у нас на тело массой m1 действует сила, которая изменяется по закону F = Fo*cos(w*T), где w- круговая частота, T- текущее время, а Fo- максимальное значение силы, которое в программе Raketa будем задавать как Fo= mg1*Vgo. Таким образом, для всех ниже рассмотренных примеров у нас при тех исходных данных, что мы задавали, рассматривая разгон топливной и безтопливной ракет, Fo будет 5*200=1000 Н, а m1 будет 1000 кг.

Давайте вычислим какова будет скорость тела массой m1 при круговой частоте изменения силы w = 0,5 рад/с. Дифференциальное уравнение, которое будет описывать движение массы, у нас будет (44). У него есть аналитическое решение и оно для скорости массы в момент времени T будет (45), а для пути пройденного этой массой (46), где V1 это начальная скорость массы, т.е. в момент времени T=0. А, если мы опишем движение этой массы в приращениях, то мы получим уравнения (47) и (48), где V1 это скорость в начале шага решения P0, т.е. в момент времени T1, а V2 это скорость в конце шага решения (шага приращения времени), т.е. в момент времени T2=T1+P0, и то же самое для S1 и S2. Чтобы наглядно были видны погрешности решения, возможные при численном решении, давайте сравним аналитическое решение с численным решением методом Эйлера, которые даны на рис.14.

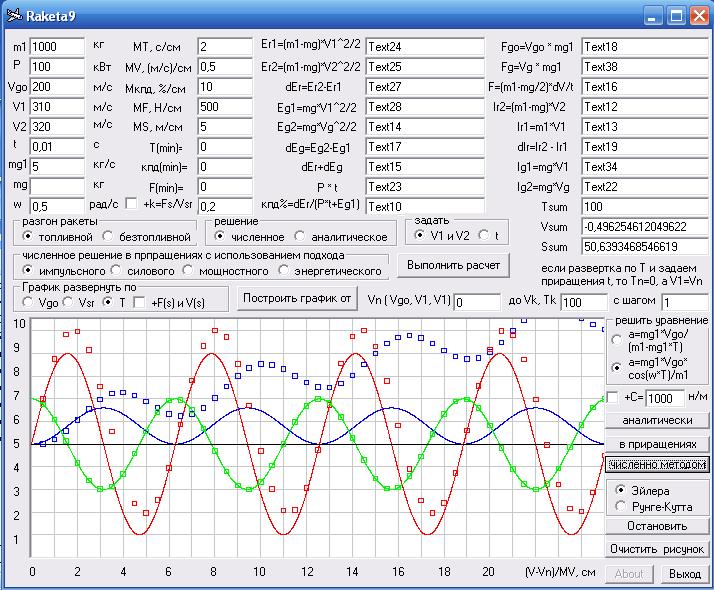
Рис.14. Сравнение точности решения задачи при воздействии на массу периодической силы. Сплошные линии – аналитическое решение дифференциального описания (44) и квадратики – численное решение методом Эйлера с шагом 1 с. Зеленые точки – сила, красные – скорость и синие – смещение тела в функции времени. Скриншот программы Raketa9.

m1*dV/dt=Fo*cos(w*T)                                                             (44)

V = V1 + Fo*sin(w*T) / (m1*w)                                                (45)

S = V1*T + Fo* (1 - cos(w*T)) / (m1*w^2)                               (46)

V2 = V1 + ΔV= V1 + P0*Fo* cos(w*(T1+P0/2)) / m1              (47)

S2 = S1 + P0 * (V1+V2)/2                                                          (48)

Здесь мы явно видим, что метод Эйлера для решения таких задач не подходит, т.к. у него идет постоянное запаздывание по используемой в расчетах скорости, что наглядно было видно и на рис. 13, а в результате мы имеем камулятивное накопление ошибки по смещению. А вот метод Рунге-Кутта для дифференциального описания и описание в приращениях, как мы это видим на рис. 15, прекрасно справляются с этой задачей при том же шаге решения 1 с. Здесь у нас на графиках скорости и перемещеня при решении описания в приращениях (кружки) совпали с решением дифференциального описания методом Рунге-Кутта (квадратики) и хорошо легли на линии аналитического решения. А вот на графике силы мы видим, что кружки и квадратики не совпали друг с другом, хотя и те и те хорошо легли на линию аналитического решения. Это объясняется тем, что при численном решении дифференциального уравнения сила вычислялась четыре раза и я вывел на график ее значение для времени в конце шага решения, как и для скоростей и перемещений, а при решении задачи в приращениях нам нужна была сила на середине шага решения, где я ее и вычислял, поэтому и на график я вывел ее значение для этого момента времени. 

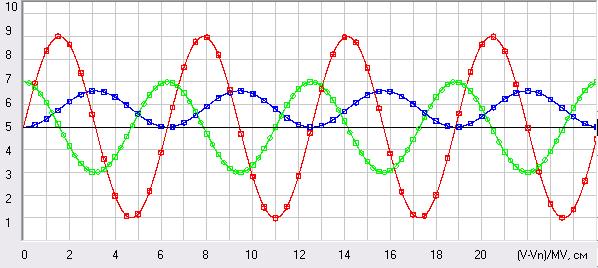
Рис. 15. Решение задачи при воздействии на массу периодической силы. Сплошные линии – аналитическое решение дифференциального описания (44), квадратики – его численное решение методом Рунге-Кутта с шагом P0=1 с и кружки - описание (оно же и решение) в приращениях (47) и (48) с шагом P0=1 с. Скриншот программы Raketa1.

Но самым жестким тестом на точность решения задачи тем или иным методом является режим резонанса в системах, поэтому давайте рассмотрим и систему, где на массу будет действовать не только внешняя периодическая сила, но и внутренняя сила возникающая в пружине жесткостью С, с которой соединена наша масса. Дифференциальное описание данной системы будет (49). Это уравнение тоже имеет аналитическое решение для скорости (50) и отклонения от положения равновесия системы (51). А, если у нас начальная скорость V1=0, то получатся более простые формулы (50') и (51'), где k = (C / m1)^0,5 это собственная частота колебаний этой системы. А описание данной системы в приращениях (оно же решение) будет (52) и (53), где V1 это скорость в начале шага решения P0, т.е. в момент времени T1, а V2 это скорость в конце шага решения (шага приращения времени), т.е. в момент времени T2=T1+P0, и то же самое для S1 и S2.  

m1*dV/dt = -C * S + Fo*cos(w*T)                                                                                        (49)

V = V1*k*(m1 / C)^0,5*cos(k* T) + Fo*(k*sin(k*T) - w*sin(w*T)) / (C – m1*w^2)        (50)

S = V1*(m1 / C)^0,5*sin(k*T) - Fo*(cos(k*T) - cos(w*T)) / (C – m1*w^2)                       (51)

V = Fo*(k*sin(k* T) - w*sin(w*T)) / (C – m1*w^2)                                                            (50’)

S = Fo*(cos(w*T) - cos(k* T)) / (C – m1*w^2)                                                                    (51’)

V2=V1 + ΔV= V1 + P0*(Fo*cos(w*(T1+P0/2)) - C*S1) / (m1 + C*P0^2 / 2)                    (52)

S2=S1 + P0*(V1+V2)/2                                                                                                         (53)

К сожалению, аналитическое решение уравнения (49) не имеет, так сказать, решения потому, что в знаменателе формул (50) и (51) получается ноль, а делить на ноль нельзя. А получается это потому, что при резонансе у нас частота вынужденных колебаний должна совпадать с частотой собственных колебаний системы, т.е. w должно быть равно k=(C/m1)^0,5. И, если мы подставим это значение w в формулы (50) и (51), то у нас в знаменателе получится C-C. А при численном решении уравнения (49) никаких проблем не возникает. Их не будет и при описании этого процесса в приращениях. Смотрите рис. 16 при жесткости С=1000 Н/м и частоте w=1 рад/с. Там все графики практически совпадают, но все же имеется маленькое отличие. Вот только не понятно какое решение более точное – дифференциального описания (49) методом Рунге-Кутта или решение в приращениях (52) и (53).

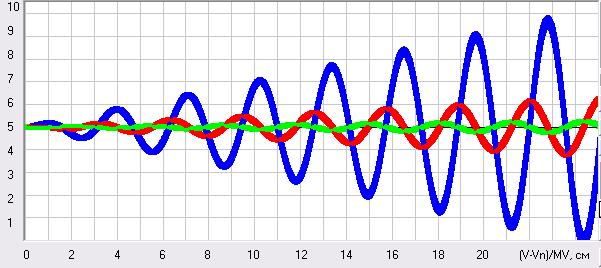
Рис. 16. Режим резонанса при решении дифференциального описания (49) методом Рунге-Кутта и решении задачи в приращениях (52) и (53) при шаге решения (приращения) 0,01 с. Масштабы были следующие MT=2 с/см, MV=20 (м/с)/см, MS=5 м/см и MF=100 кН/см. Скриншот программы Raketa1.

Выяснить мы это сможем, если рассмотрим режим биений, т.е. режим близкий к резонансному, когда частота вынужденных колебаний немного отличается от частоты собственных колебаний системы. Кстати, если мы зададим частоту вынужденных колебаний w=0,999*k, то мы получим по формулам аналитического решения в начале процесса резонанса почти точное решение для режима резонанса, но мы возьмем эту частоту такой, чтобы у нас в обозримом времени явно просматривалось несколько циклов биений. Пусть у нас жесткость так и останется 1000 Н/м, т.е. частота собственных колебаний так и будет 1 рад/с, а частоту вынужденных колебаний зададим 0,95 рад/с. Биения в системе, возникающие при таких параметрах вы видите на ниже приведенных рисунках 17, 18 и 19, где тонкие сплошные линии это аналитическое решение дифференциального описания системы (49), а толстые линии, в которые слились квадратики и кружки, это решение этого описания методом Рунге-Кутта и решение описания в приращениях. Как видим, на рис. 17 у нас оба решения практически слились, т.е., если погрешность численного решения методом Рунге-Кутта и есть, то она даже при шаге решения 0,01 с очень маленькая. А вот решение в приращениях с таким шагом дает очень большую погрешность (рис. 18), но может быть она станет такой же при шаге решения 0,0025 с, когда время решения этой задачи на компьютере методом Рунге-Кутта и в приращениях будет примерно одно и то же и тогда можно будет говорить о равнозначности точности этих решений. Ответ на этот вопрос дают графики на рис. 19.

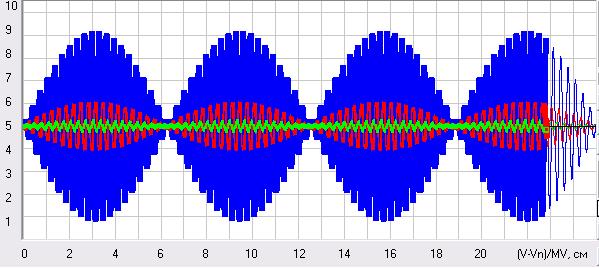
Рис. 17. Режим биений при решении дифференциального описания (49) методом Рунге-Кутта при шаге решения 0,01 с. Масштабы были следующие MT=20 с/см, MV=20 (м/с)/см, MS=5 м/см и MF=100 кН/см. Скриншот программы Raketa1.

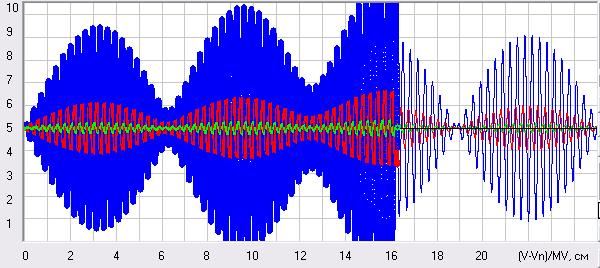
Рис. 18. Режим биений при решении задачи в приращениях (52) и (53) при шаге решения (приращения) 0,01 с. Масштабы были следующие MT=20 с/см, MV=20 (м/с)/см, MS=5 м/см и MF=100 кН/см. Скриншот программы Raketa1.

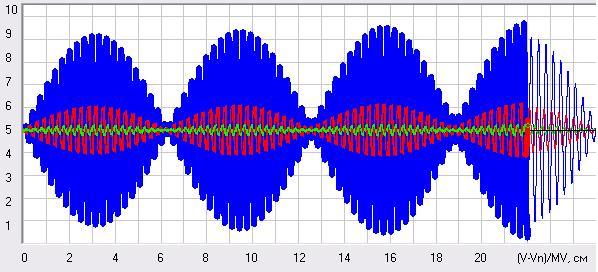
Рис. 19. Режим биений при решении задачи в приращениях (52) и (53) при шаге решения (приращения) 0,0025 с. Масштабы были следующие MT=20 с/см, MV=20 (м/с)/см, MS=5 м/см и MF=100 кН/см. Скриншот программы Raketa1.

Как видим, решение в приращениях даже при шаге решения 0,0025 с, хоть и стало гораздо лучше, чем при шаге решения 0,01 с, но все равно гораздо хуже, чем при решении методом Рунге-Кутта при шаге решения 0,01 с. Таким образом, в общем случае описание систем в приращениях при том же времени решения задачи на компьютере не может соперничать по точности решения с решением дифференциального описания методом Рунге-Кутта. Хотя, например, для экономических систем описание в приращениях и является единственно возможным описанием, т.к. хотя, как я отмечал в работе [6], в этих системах и наблюдаются инерционные свойства систем, как и в механических системах, но дифференциальное описание ускорений для процессов в этих системах получить не удается. Поэтому описание явлений Природы и искусственных систем в приращениях все же может в некоторых случаях соперничать с дифференциальным описанием и последующим решением этого описания методом Рунге-Кутта. Я здесь ничего не говорю о преимуществах аналитического решения для дифференциального описания, т.к. для реальных систем, а не для учебных, получается такое дифференциальное описание, которое никогда не имеет аналитического решения.

А сейчас давайте немного остановимся на допустимых погрешностях численного решения задач, т.к. мы чаще всего не можем даже оценить эту погрешность из-за того, что при решении реальных задач у нас полученный ответ просто не с чем сравнить, т.к. у нас нет аналитического решения. Да, здесь чем меньше шаг решения и чем выше разрядность представления данных, которую может обеспечить наша операционная система на компьютере и используемый язык программирования, тем будет меньше погрешность решения из-за округления данных в последней значащей цифре, которая будет кумулятивно накапливаться. Но вместе с тем у нас, чем меньше шаг решения, тем больше будет время работы компьютера при решении нашей задачи, поэтому погрешность численного решения всегда должна определяться компромиссно со временем решения задачи. Например, для оптимизации абсолютной скорости Солнечной системы и скорости гравитации мне надо на математической динамической механической модели Солнечной системы проводить десятки вычислительных экспериментов по планам многофакторного планирования. И для 6-и факторного рототабельного плана мне надо провести 79 экспериментов, каждый из которых для определения, например, параметров орбиты Меркурия длится около 7 часов. Итого на весь план требуется 553 часа, т.е. при непрерывной работе компьютера это будет 23 дня. А, если учесть, что мне надо выполнить десятки таких планов, то время работы компьютера измеряется уже годами. И это не считая времени для составления этих планов и обработки данных вычислительных экспериментов.

Да, сейчас я использую четырехядерный компьютер и это позволяет сократить время его работы почти в четыре раза, т.к. я запускаю программу Solsys7mm сразу четыре раза на каждом из ядер, но все равно время работы получается очень большим. И это при том, что я решаю задачу с основным шагом решения P0=3600 секунд, т.е. один час, а если задать шаг решения 900 секунд, то время работы компьютера опять увеличится в четыре раза. А нам, конечно же, хочется максимально сократить время решения задачи и чтобы при этом значительно не пострадала точность решения, но как быть в тех случаях, когда нам получившийся ответ не с чем сравнить. Я в таком случае использую следующий прием - запускаю программу на решение задачи с известными начальными данными, а затем в некоторый момент останавливаю ее и включаю обратное течение времени. Когда время опять станет равно нулю, останавливаю программу и смотрю какие получились данные и сравниваю их с начальными. Например, в программе Udar3 я задаю начальные скорости шаров до удара, а потом после удара останавливаю программу и, задав скорости с другим знаком, опять запускаю ее и у меня шары осуществляют обратный удар. После этого сравниваю получившиеся скорости с теми, что я задавал в начале вычислительного эксперимента.   

А теперь давайте посмотрим насколько точен метод Рунге-Кутта для решаемой мною задачи в программе Solsys7m при используемом мною основном шаге решения P0=3600 секунд. Для этого зададим начальные данные, т.е. координаты и скорости планет, например, на 1.01.1801 года и проведем вычислительный эксперимент до 2000 года со скоростью гравитации равной бесконечности, когда не будет учитываться ни запаздывание по координатам, ни динамическое давление (это надо, чтобы процесс был обратимым). При этом запишем координаты и скорости Меркурия в файл на начало эксперимента и для большей статистики через год (надо в программе Solsys7m отметить чекбокс «Записать координаты X, Y, Z», а, чтобы записалась и энергия системы и ее момент количества движения, надо включить и их расчет, т.е. отметить чекбокс «dEsys, dMsys, %» и при этом запись можно включать только в нужные моменты времени). А в 2000 году остановим программу, включим реверс времени и продолжим вычислительный эксперимент назад, т.е. до 1.01.1801 года, и при этом опять запишем координаты и скорости Меркурия в файл. А затем сравним координаты Меркурия в начале вычислительного эксперимента и в конце, т.е. через 400 лет по данным, которые я привожу ниже для начала 2-го января 1801 года и для полудня 1-го января 1802 года.

Меркурий

прямое движение

02,000.01.1801____T= 000000000,043____X= -000059162,534____Y= -000014285,789____Z= 000004296,188

____Rpl= 000060621,571____VX= 0001334,196____VY= -0045204,122____VZ= -0003803,996

                      ____Vpl= 0045383,511____Esys= 000196829,496____MKDsys= 31344042178561,600

обратное движение

02,000.01.1801____T= 000000000,043____X= -000059162,536____Y= -000014285,743____Z= 000004296,192

____Rpl= 000060621,571____VX= -0001334,161____VY= 0045204,130____VZ= 0003803,993

                      ____Vpl= 0045383,518____Esys= 000196829,502____MKDsys= -31344044042226,600

прямое движение

01,500.01.1802____T= 000000031,536____X= -000040782,914____Y= -000054803,302____Z= -000000711,703

____Rpl= 000060621,571____VX= 0029279,629____VY= -0026677,028____VZ= -0004874,886

                       ____Vpl= 0039908,959____Esys= 000196849,349____MKDsys= 31349381807414,400

обратное движение

01,500.01.1802____T= 000000031,536____X= -000040782,943____Y= -000054803,275____Z= -000000711,698

____Rpl= 000060621,571____VX= -0029279,612____VY= 0026677,051____VZ= 0004874,886

                      ____Vpl= 0039908,962____Esys= 000196849,352____MKDsys= -31349382509667,300

Из приведенных данных видно, что погрешность численного решения по координатам на эти две даты в километрах будет dX=2, dY=46, dZ=4 и dX=29, dY=27, dZ=5, а погрешность по скоростям в метрах в секунду будет dVX=0,035, dVY=0,008, dVZ=0,003 и dVX=0,017, dVY=0,023, dVZ=0,000, что, для используемых нами астрономических расстояний и скоростей, является незначительной погрешностью. Ведь даже для орбиты Меркурия погрешность в 28 километров будет составлять погрешность по долготе всего в 1 угл.сек., а для остальных планет она будет гораздо меньше. А т.к. здесь время вычислительного эксперимента у нас было 400 лет, то для прямого эксперимента за 200 лет  погрешность будет в два раза меньше.

При этом для всех остальных планет, скорость которых значительно меньше скорости Меркурия, погрешность по координатам и скоростям будет совсем маленькой. Например, для Земли при аналогичном расчете мы получим погрешность решения по координатам менее 1 километра, а по скоростям менее 1 мм/с, т.к. данные на две зафиксированные даты полностью совпадают (а сколько будет погрешность конкретно я не могу сказать, т.к. не предусмотрел более точный формат вывода данных в файл). Но, не только по знакам скоростей можно понять в приведенных ниже данных, что это действительно разные записи для одного и того же времени. Ведь энергия системы и момент количества движения системы, уменьшенные в файлах в 10^30 раз, получаются тоже разные в начале эксперимента и в конце, хотя полностью совпадают с аналогичными значениями, полученными, когда мы проверяли координаты Меркурия. Здесь правда в расчете у Меркурия и у Земли имеется расхождение по моменту количества движения в 15-м знаке, но это последняя значащая цифра, которую позволяет получить язык программирования Visual Basic 6, поэтому и расхождение.

Земля

прямое движение

02,000.01.1801____T= 000000000,043____X= -000035550,167____Y= 000142746,658____Z= 000000063,468

____Rpl= 000147106,316____VX= -0029398,911____VY= -0007306,458____VZ= -0000004,396

                     ____Vpl= 0030293,239____Esys= 000196829,496____MKDsys= 31344042178561,600

обратное движение

02,000.01.1801____T= 000000000,043____X= -000035550,167____Y= 000142746,658____Z= 000000063,468

____Rpl= 000147106,316____VX= 0029398,911____VY= 0007306,458____VZ= 0000004,396

                      ____Vpl= 0030293,239____Esys= 000196829,502____MKDsys= -31344044042227,000

прямое движение

01,500.01.1802____T= 000000031,536____X= -000033746,235____Y= 000143288,150____Z= 000000064,968

____Rpl= 000147106,316____VX= -0029495,338____VY= -0006919,713____VZ= -0000004,107

                      ____Vpl= 0030296,162____Esys= 000196849,349____MKDsys= 31349381807414,400

обратное движение

01,500.01.1802____T= 000000031,536____X= -000033746,235____Y= 000143288,150____Z= 000000064,968

____Rpl= 000147106,316____VX= 0029495,338____VY= 0006919,713____VZ= 0000004,107

                       ____Vpl= 0030296,162____Esys= 000196849,352____MKDsys= -31349382509667,500

Можно, конечно, получить на программе Solsys7m решение и для Меркурия гораздо более точное и, если уменьшать основной шаг решения в 4-е раза до 900 сек, то у нас, также, как и для Земли при шаге 3600 сек, координаты и скорости в пределах той точности, что я записывал их в файл, полностью совпадут, т.е. погрешность решения по координатам будет менее 1 километра, а по скоростям менее 1 мм/с. Вот только такой шаг решения для остальных планет будет слишком маленьким и для внешних планет можно использовать шаг решения даже в несколько дней. Но у меня в программе не предусмотрено решение для разных планет с разными шагами, поэтому шаг решения для всех планет определяется по самой быстрой планете так, чтобы ее движение было найдено с приемлемой точностью. А, если уменьшить шаг решения, то у нас увеличится время работы компьютера, что при многих сотнях экспериментов, что мне надо провести, для меня очень критично, поэтому я выбрал компромиссный вариант между приемлемой точностью решения для Меркурия и приемлемым временем работы компьютера.

Здесь надо сказать и то, что у самого языка программирования Visual Basic 6, на котором написана программа Solsys7m, точность вычислений не очень большая и быстродействие у него из-за наличия виртуальной машины, т.е. библиотеки msvbvm60.dll, не очень высокое, но я выбрал именно этот язык для своей программы Solsys7m, т.к. считаю его самым подходящим языком для научных работников, которые далеки от тонкостей вопросов программирования и которым надо думать не над кодом программы, а над физическим содержанием решаемой задачи. А более подробно узнать, почему я считаю этот язык самым подходящим для научных работников, можете в моей статье [15], если, конечно же, Вам это надо.

Ну, а, если кого-то не устраивает точность вычислений или быстродействие моей программы Solsys7m, то они могут написать аналогичную программу на других языках программирования. Можно даже на том же бэйсике, например, на FreeBasic, но это будет сделать посложнее, чем на Visual Basic 6. Можно и, например, на Delphi, а уж слишком грамотные в программировании могут написать даже на c++, у которых и быстродействие побольше и имеется возможность использовать не только 8-и битное представление данных, как в Visual Basic 6, но и 10-и битное. Вот только писать и отлаживать они будут программу подобную моей Solsys7m, например, на с++ лет пять, а я за это время и программу уже создал и надеюсь закончить все свои исследования по данному вопросу. И при этом, 10-и битный формат в десятиричной системе счисления даст к 15-и значащим цифрам в Visual Basic 6 прибавку только на 4-е значащих цифры. Вот, если бы написать программу на фортране, то там можно удвоить количество значащих цифр, но, к сожалению, я не смог найти подходящих версий фортрана для современных компьютеров.

А вот быстродействие программы можно легко увеличить и используя процессоры с 64-х битной разрядностью и, соответственно, операционные системы, т.к. там можно использовать оперативную память свыше 4 гигабайт. Хотя есть и еще один несложный вариант повышения быстродействия – это написание библиотеки dll на FreeBasic для самого критичного участка программы, а именно для подпрограммы Diffur21 и пример такого решения я приводил в своей статье [15]. Ну, и существенное увеличение быстродействия мы получим на 4-х ядерных компьютерах, где можно запустить одновременно на выполнение одну и ту же программу сразу 4-е раза, т.е. за то же время программа будет выполнена 4-е раза, но тут уж Вы сами смотрите, что Вам надо в конечном итоге.

                                                                                  Выводы

1. Явления Природы (различные системы) могут быть описаны на языке математики с использованием различных физических подходов (импульсного, силового, мощностного и энергетического).

2. Описание явлений Природы может быть как интервальным (конечное или в приращениях) так и мгновенным (дифференциальным).

3. Описание в приращениях является аналогом дифференциального описания, но может быть получено с использованием всех подходов, а дифференциальное только с использованием силового и мощностного.

4. Описание с использованием уравнений Лагранжа 2-го рода, во-первых, является не корректным с теоретической точки зрения, т.к. происходит смешивание энергетического и силового подходов, а, во-вторых, в современных условиях не имеет никакой практической ценности, т.к. для практического использования описания реальных систем нам нужно описание не в обобщенных координатах, позволяющих уменьшить число уравнений описывающих систему, а описание в обычных координатах, которое, при наличии компьютеров, становится возможным осуществить.

5. Для дифференциального описания динамических систем следует использовать или силовой подход Эйлера, если позволяет система, или в общем случае мой мощностной подход, а при наличии в системе связей заменять жесткие соединения элементов системы упругими элементами и демпферами.

6. Метод Рунге-Кутта по 4-м коэффициентам для численного решения дифференциальных уравнений, описывающих поведение систем, является очень точным и устойчивым методом и поэтому его можно безбоязненно использовать для решения уравнений описывающих практически любые системы.  

P.S. Я конечно же много критиковал в этой статье математиков за то, что они из-за отсутствия математических способностей переквалифицировались в математико-физиков и может быть, где-то я был и не прав, но и Вы поймите меня. Я вот при написании статьи «Опять о принципе наименьшего действия» столкнулся с проблемой, которую математики не могут решить уже лет 300, т.е. разрешить спор двух создателей вариационного исчисления Эйлера и Лагранжа о том варьируется там время или нет. И тут получается как в анекдоте. Я их спрашиваю - кто прав, а они отвечают и Эйлер прав и Лагранж прав. Я говорю, что такого не может быть, а они отвечают, что и Вы правы. Вот и все на что способны современные математики, которые в основной массе являются математико-физиками (не путать с физико-математиками, коих считанные единицы). Я, конечно, имею, как механик, свое мнение по этому вопросу и считаю, что время вообще не может присутствовать в вариационном исчислении, но хотелось бы увидеть чисто математические выкладки по этому вопросу.

А сейчас вот занялся поиском скорости гравитации с использованием планов многофакторного планирования и опять у меня возникают сложности из-за математиков, т.к. все эти планы показывают отличные результаты, когда критерием оптимизации является сам отклик системы. А мне надо оптимизировать параметры по отклонению (причем по абсолютной величине) отклика системы от оптимального значения. Я уже писал об этой проблеме в статье «Аномальные смещения параметров орбит планет», где на конкретных тестах показал, что по этому критерию оптимизации все планы (ортогональные, рототабельные и т.д.) показывают очень удовлетворительные результаты. Но математики упорно лезут в физику, где они сто лет не нужны, а вот заняться своими математическими проблемами никак не хотят. А я был бы им признателен, если бы они разработали планы многофакторного планирования, где можно производить оптимизацию параметров систем по критерию отклонения отклика системы от оптимального значения (как по абсолютной величине, так и этого отклонения в квадрате). И, как бы не была печальна ситуация в современной науке, я все же надеюсь, что, после этого моего крика вопиющего в пустыне, хоть один математик займется реальной математикой.

                                                                     Список литературы

принятые сокращения - МКМ-2- цикл статей "Механика для квантовой механики" часть 2

                                         СГ-3-      цикл статей "Скорость гравитации" часть 3

1. - Л.Ландау, Л.Пятигорский, Механика. – М-Л.: Техтеорлит, 1940. - 200 с.

2. - Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Т.1. Механика. - М.: Физматлит, 1958. - 206 с.

3. - Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособие в 10-ти т.Т.1. Механика. - 5-е изд. М.: Физматлит, 2004. - 224 с.

4. - Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособие в 10-ти т.Т.2. Теория поля. - 7-е изд. М.: Физматлит, 1988. - 512 с.

5. - Юдин С.Ю. //Методы оценки эффективности применения МТА и оптимизации их параметров с использованием математических моделей/ диссертация на соискание ученой степени кандидата технических наук, Волгоград.: 1991, 270 с.

6. - Юдин С.Ю. //Моделирование систем и оптимизация их параметров//. Волгоград, 2006, 213 с.   программа-просмотрщик с анимациями  http://modsys.narod.ru/Stat/Reader5m_exe.rar , текстовый файл http://modsys.narod.ru/Stat/Reader5m_doc.rar

7. - Юдин С.Ю. МКМ-1 //Две меры механической формы движения материи//. 2005, 16 с.      http://modsys.narod.ru/Stat/Stat_Est/Udar/udar.html

8. - Юдин С.Ю. МКМ-2 //О принципах кратчайшего времени и наименьшего действия// 2005, 20 с. http://modsys.narod.ru/Stat/Stat_Est/Princip/princip.html

9. - Юдин С.Ю. МКМ-3 //О формуле Планка и кванте действия// 2005, 26 с. http://modsys.narod.ru/Stat/Stat_Est/Plank/plank.html

10.- Юдин С.Ю. МКМ-4 //Опять о принципе наименьшего действия//  2010, - 43 с http://modsys.narod.ru/Stat/Stat_Est/Princip2/princip21.html

11. - Юдин С.Ю. СГ-1 //О равноденствиях Гиппарха и Птолемея// 2010, 55 с. http://modsys.narod.ru/Stat/Stat_Est/Hipp_Ptolo/Hipp_Ptolo2.html

12. - Юдин С.Ю. СГ-2 //Кинематическая теория планет//.  2012, 72 с http://modsys.narod.ru/Stat/Stat_Est/Kinematik/Kinematik1.zip

13. - Юдин С.Ю. СГ-3 //Аномальные смещения параметров орбит планет//  2012, - 32 с   http://modsys.narod.ru/Stat/Stat_Est/Anomal/Anomal1.html

14. - Юдин С.Ю. СГ-4 //Влияние скорости гравитации на смещения параметров орбит планет//  2013, - 145 с http://modsys.narod.ru/Stat/Stat_Est/Vlijanie2.html

15. - Юдин С.Ю. //Выбор языка программирования для научных работников// 2007, 24 с. http://modsys.narod.ru/Stat/Stat_Prog/Vibor/Vibor2.html

16. – Ньютон Исаак. Математические начала натуральной философии. - М.: Наука, 1989, 688 с.

17. - Герц Г. Принципы механики, изложенные в новой связи. М.: Академия наук СССР, 1959, 386 с.

18. - Лагранж Аналитическая механика. Т.1 М-Л.: ОНТИ-НКТП, 1938, 348 с.  

        Лагранж Аналитическая механика. Т.2 М-Л.: ОНТИ-НКТП, 1950, 440 с.  

19. - Эйлер Л. Основы динамики точки. М-Л.: ОНТИ-НКТП, 1938, 500 с.   http://narod.ru/disk/3486349000.68bf093210ba8df860be54c7ad004003/Euler_1938_4.pdf.html

20. - Полак Л.С. Вариационные принципы механики // Вариационные принципы механики с. 780-879// Под ред. Л.С. Полака, М.: Физматгиз, 1959, 932 с. http://ftp.kinetics.nsc.ru/chichinin/pmlic.htm#P

21. – Григорьян А.Т., Полак Л.С. Основные идеи механики Генриха Герца (статья размещена в книге Г.Герц  //Принципы механики, изложенные в новой связи//, см. п.17).

22. - Гербер П. //Пространственное и временное распространение гравитации// http://bourabai.kz/articles/gerber/gerber-rus.htm

23. –Эйнштейн А. Объяснение движения перигелия Меркурия в общей теории относительности. Собрание научных трудов. Том 1. М.: Наука, 1965, 701 с.

24. - Циолковский К.Э. Труды по реактивной технике. //Исследование мировых пространств реактивными приборами (1926) с. 103...177// М.: ОБОРОНГИЗ, 1947, 368 с.

25. - Девитт Брайс Ф. Динамическая теория групп и полей. М.: Наука, 1987 г. 

http://bookfi.org/dl/453421/8fcfca

26. - Вепринцев В.С. //Об алгоритмах преобразований Галилея и Лоренца и динамике// http://vvs-ya.narod.ru/about12.htm

27. - Смульский И.И. Теория взаимодействия. Новосибирск: Из-во Новосиб. Ун-та, НИЦ ОИГГМ СО РАН, 1999, 294 с. http://www.ikz.ru/~smulski/TVfulA5_2.pdf

28. - Сухоруков Г.И., Сухоруков В.И., Сухоруков Э.Г, Сухоруков Р.Г. Реальный физический мир без парадоксов. Братск. БрГТУ, 2001 – 229 с.    http://suxorucov.narod.ru/Kniga.rar

29. - Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Т.2. М.: Наука, 1972 .

P.P.S. Все мои работы можно найти на моих сайтах в разделе "Научные работы", а всю другую литература в разделе "Моя библиотева".